B. Some sample problems solved in other books

Mahdi Abdeljaouad; Jeffrey Oaks

B. Some sample problems solved in other books

Chapter structure

Download Chapter

TY  - CHAP
T1  - B. Some sample problems solved in other books
T2  - Al-Hawārī’s Essential Commentary: Arabic Arithmetic in the Fourteenth Century
A1  - Mahdi Abdeljaouad
A1  - Jeffrey Oaks
AB  - Al-Hawārī completed his Essential Commentary in Marrakesh in 1305. This modest book was written with the goal of supplying numerical examples to the rules of calculation explained in the famous Condensed Book on the Operations of Arithmetic of his teacher Ibn al-Bannāʾ. It is partly because of its modesty that al-Hawārī’s book is a good vehicle for presenting the various facets of practical Arabic arithmetic, which in al-Hawārī’s time included not just computational techniques but also algebra and other problem-solving methods. In this book we give an edition, English translation, and running commentary of al-Hawārī’s commentary, together with a general introduction to Arabic arithmetic to situate it in context. We cover not just the rules for operating on known and unknown numbers, but also their conceptual and historical background. Numbers in Arabic arithmetic were conceived as amounts or measures of something, and thus could be any positive quantity, including fractions and irrational roots. Thus they were neither founded in the Greek notion of multitudes of an indivisible unit, nor were they defined axiomatically as they are today. This way of understanding numbers informed both their ways of expressing numbers and algebraic expressions and how they performed their calculations. On the historical front, we witness the ways that different local arithmetical traditions interacted, and how Greek arithmetic, even if fundamentally incompatible with its Arabic counterparts, was partially absorbed into practical books like al-Hawārī’s.
PB  - Max-Planck-Gesellschaft zur Förderung der Wissenschaften
PY  - 2021
SN  - 978-3-945561-63-8
L1  - https://edition-open-sources.org/media/sources/14/7/sources14_chap07.pdf
LK  - https://edition-open-sources.org/sources/14/7/index.html
C1  - by-sa
DO  - 10.34663/9783945561638-07
LA  - english
ER  -

[1] A problem of Ibn al-Bannāʾ’s solved by “the four proportional numbers”.

In some problems, the method of “the four proportional numbers” is applied directly. This example is from the chapter on business transactions (muʿāmalāt) in Ibn al-Bannāʾ’s Essays on Arithmetic. It asks for the price of a certain amount of a commodity given the price of another amount of the same commodity.¹

If someone said to you, “Five amdāʾ² for ten dinars.³ How much do fourteen mudy cost?”

These are four proportional amounts: the first is ten dinars, the second is five amdāʾ, the third is the unknown dinars, and the fourth is fourteen mudy. The third in this problem is the unknown. You multiply the first by the fourth, and you divide the outcome by the second, giving you the third, which is the cost of fourteen mudy, the unknown, and that is twenty-eight dinars.

[2] A problem of Ibn al-Bannāʾ’s solved by single false position.

This problem, also from Ibn al-Bannāʾ’s Essays on Arithmetic, shows how the method of “the four proportional numbers” is used in single false position. In this method a convenient but probably incorrect value is posited for the solution, here 60, and the calculations are performed on this value. The answer is then found from a proportion.⁴

If someone said to you, “A quantity (māl): you add its half and a third of what remains, and a fourth of what remains, and a fifth of what remains, to get twenty dirhams. How much is the quantity?”

You can take the third and the fourth and the fifth of sixty. Then take its half, giving thirty. And take a third of what remains, giving ten, which leaves twenty. Take its fourth, giving five. There remains fifteen. Take its fifth, giving three. Then gather the thirty with the ten and the five and the three, and you add them all, so the sum is forty-eight.

The ratio of this forty-eight with respect to the sixty is as the ratio of the twenty with respect to the unknown quantity. So you work it out as described above to get the quantity, which is fifteen.

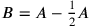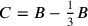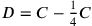Like al-Hawārī’s problem at 200.1, this enunciation requires some explanation. If we use modern notation and call the unknown , and we make the remainders $B=A-{1\over 2}A$ , $C=B-{1\over 3}B$ , and $D=C-{1\over 4}C$ , then the problem asks to add together 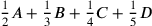${1\over 2}A+{1\over 3}B+{1\over 4}C+{1\over 5}D$ . It would not be efficient to solve this problem by algebra, either premodern or modern. If we let the unknown be 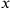, then the equation would be set up as 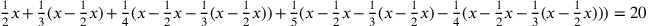${1\over 2}x+{1\over 3}(x-{1\over 2}x)+{1\over 4}(x-{1\over 2}x-{1\over 3}(x-{1\over 2}x))+{1\over 5}(x-{1\over 2}x-{1\over 3}(x-{1\over 2}x)-{1\over 4}(x-{1\over 2}x-{1\over 3}(x-{1\over 2}x)))=20$ . Even if you manage to simplify this to 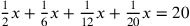${1\over 2}x+{1\over 6}x+{1\over 12}x+{1\over 20}x=20$ , it is much easier to pick a value like 60 and work through the operations with it.

For another problem solved by single false position, see problem [7] below.

[3] Ibn Qunfudh’s problem (14), solved by algebra.

Problems [3], [4], and [5] are simple examples that show how the rules illustrated by al-Hawārī in the chapter on algebra are applied in the algebraic solutions to problems. For each problem, we give the breakdown according to the three stages. These stages are not indicated in the texts.

Ibn Qunfudh completed his commentary on Ibn al-Bannāʾ’s Condensed Book in 1370. It is titled Lowering the Veil from the Faces of Arithmetical Operations. This book shows the algebraic notation.⁵

[Enunciation] Problem. Ten: you divide it into two parts, and you multiply one of them by the other, resulting in twenty-two and two ninths.

[Stage 1] Make one of the parts a thing and the other ten less a thing, and multiply one of them by the other, resulting in ten things less a māl, and it is equal to twenty-two and two ninths, and it is this: ${t\atop 10}~\ell ~{m\atop 1}=22{2\over 9}$ .

[Stage 2] So you restore by adding the excluded [amount] to each [side], so the problem becomes: ten things equal a māl and twenty-two and two ninths, and it is this: ${t\atop 10}={m\atop 1}~~22{2\over 9}$ .

[Stage 3] This results in the fifth type [of equation]. So work it out, which is that you halve the roots and you square the half to get twenty-five. Subtract the number from it, leaving two and seven ninths. Take its root, to get one and two-thirds. And if you add it to the half, which is five, it results in the thing by addition, and if you subtract it, it results [in the thing] by subtraction. One of them is [one] part, and the remainder from the ten is the other part. So you find one of the parts to be six and two thirds, and the other three and a third, and that’s it.

The enunciation of the problem is an arithmetic question which is solved using algebra. Ibn Qunfudh applies the rule for multiplying polynomials in stage 1, a restoration (al-jabr) to simplify the equation in stage 2, and the rule for solving the type 5 equation in stage 3. The type 5 equation here has two solutions, and in this problem they lead to the two parts of ten. The two equations in notation are shown as and in the manuscript. 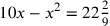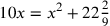They correspond to the modern $10x-x^2=22{2\over 9}$ and $10x=x^2+22{2\over 9}$ , respectively. In this problem Ibn Qunfudh shows “things” in notation with only the three dots from the letter , though he shows the whole letter in other examples.

[4] A geometry problem of al-Karajī’s solved by algebra.

This next problem is from al-Karajī’s Sufficient Book on Arithmetic, written in the early eleventh century. There is no need for stage 2 because the equation that is set up at the end of stage 1 is already simplified. Its solution in stage 3 is trivial.⁶

[Enunciation]If someone said, “A rectangle: its length is twice its width, and its area is equal to its perimeter. How much are its area and its sides?”

[Stage 1]Make its length two things and its width a thing, and multiply the length by the width to get two māls. This is the area, and it equals the perimeter, which is six things [ ${m\atop 2}={t\atop 6}$ ].

[Stage 3]So the one thing equals three, which is the width.

[5] ʿAlī al-Sulamī’s problem (I.36), solved by algebra.

This author’s tenth-century book Sufficient Introduction on Calculation by Algebra and What One Can Learn from Its Examples contains many problems, among which is the following⁷:

[Enunciation]Two men encounter a horse. The first says to the second, if you offer a fourth and a fifth of what you have in addition to what I have, then I will have the price of the horse. And the second says to the first, if you offer a sixth and a seventh of what you have in addition to what I have, then I will have the price of the horse.

[Stage 1]So make what the first has a thing, and what the second has a number that has a fourth and a fifth, and that is twenty.⁸ If the first takes from the second a fourth and a fifth of what he has, he will have a thing and nine dirhams, which is the price of the horse.

Then the second takes from the first a sixth and a seventh of a thing, so he will have twenty and thirteen parts of forty-two of a thing, which is also the price of the horse. Then confront what they have, [i.e., establish the equation ${t\atop 1}~\hbox{9}=\hbox{20}~{t\atop {13\over 42}}$ ]

[Stage 2]and cast away like terms, leaving twenty-nine parts of forty-two equals eleven dirhams [ ${t\atop {29\over 42}}=\hbox{11}$ ].

[Stage 3]Complete the thing, by which you multiply everything you have by forty-two and divide it by twenty-nine, to get: the thing is fifteen and twenty-seven⁹ parts of twenty-nine [ $15{27\over 29}$ ], which is what the first has, and the second has twenty dirhams.

If you want the results to be whole numbers, multiply what you have by twenty-nine, so the first has four hundred sixty-two and the second has five hundred eighty.

[6] Ibn al-Bannāʾ’s problem (I.10), solved by algebra.

Many authors, Ibn al-Bannāʾ included, condensed stages 2 and 3 of their solutions. Here is the enunciation and the first of five different algebraic solutions to problem (I.10) from his Book on the Fundamentals and Preliminaries in Algebra. Note how he manipulates the operations to avoid unresolved divisions in his equation, and his justification for this manipulation after the solution.¹⁰

[Enunciation]Ten: you divide it into two parts. You divide each of them by the other, so it results in a total of four and a fourth.

[Stage 1]You make one of the parts a thing, so the other is ten less a thing. Then you square each of them and you add the squares to get a hundred and two māls less twenty things [ $\hbox{100}~{m\atop 2}~\ell ~{t\atop 20}$ ]. Keep this in mind. Then you multiply the surface of the parts by the result of the divisions, which is four and a fourth, to get forty-two things and half a thing less four māls and a fourth of a māl. This equals the sum of the remembered squares [ ${t\atop 42{1\over 2}}~\ell ~{m\atop 4{1\over 4}}=\hbox{100}~{m\atop 2}~\ell ~{t\atop 20}$ ].

[Stage 2]Then you restore and confront, to get the fifth type [of equation: ${t\atop 62{1\over 2}}=\hbox{100}~{m\atop 6{1\over 4}}$ ].

[Stage 3]So you look for the thing, finding two by subtraction, which is one of the parts, and eight by addition, which is the other part.

You saw the reason for this way above in the chapter on division, in the first part, which is: for any two numbers, if each one is divided by the other, then the sum of their squares is equal to the product of their surface by the sum of the two quotients.

We can represent the enunciation with modern algebraic notation by naming the two parts of ten and 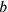so that 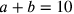a+b=10 , with the condition that 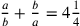${a\over b}+{b\over a}=4{1\over 4}$ . Ibn al-Bannāʾ names one of the parts “a thing”, so the other is necessarily “ten less a thing”. The modern versions would be and 10-x , and we would set up the equation as

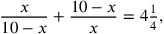
and maybe combine the terms on the left to get

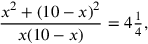
after which we would multiply both sides by x(10-x) .

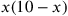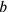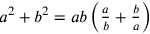Like other Arabic algebraists, Ibn al-Bannāʾ avoids operations in equations. He instead reformulates the problem according to an arithmetical rule he had given earlier in the book, and which was stated rhetorically: for any two numbers and , $a^2+b^2=ab\left({a\over b}+{b\over a}\right)$ . This way, the equation is set up without operations: “forty-two things and half a thing less four māls and a fourth of a māl…equals” “a hundred and two māls less twenty things”. There is no addition, subtraction, or scalar multiplication in this equation. Our modern version 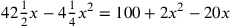$42{1\over 2}x-4{1\over 4}x^2=100+2x^2-20x$ , however, is built from addition, subtraction, scalar multiplication, and exponentiation. See our commentary above at 219.1, 219.4, and 229.8.

Because stages 2 and 3 follow prescribed rules, he does not need to spell out the steps. Like some other algebraists, Ibn al-Bannāʾ writes “restore and confront” to mean restoration and/or confrontation in stage 2. For this equation two restorations are performed.

[7] A problem of al-Ḥaṣṣār’s solved by single false position, algebra, and double false position.

Al-Ḥaṣṣār wrote his Book of Demonstration and Recollection in the Art of Dust-Board Reckoning in the late twelfth century. He is one of several authors to solve the same arithmetic problem by different methods.¹¹

If someone said to you, “A quantity (māl): you add its third and its fourth so it brings back twenty-one dirhams”.

[Solution by single false position]In this problem you can take the third and the fourth from twelve. Then you take from the twelve its third and its fourth, which is seven. The ratio of this seven with respect to twelve is as the ratio of the twenty-one with respect to the required quantity. So multiply the twelve by the twenty-one, and you divide the result by the seven. This gives you thirty-six, which is the quantity.

[Solution by algebra]And if you wish, work it out by algebra (al-jabr), which is that you make the quantity a thing. You take from it its third and its fourth, and that is three sixths of a thing and half a sixth of a thing. This equals the twenty-one [ ${t\atop {1~\,3\over 2~\,6}}=\hbox{21}$ ].

So we say to you: restore the three sixths and a half so that it yields a thing. What determines that is one and five sevenths, and we will explain it, God willing, in the chapter on the restoration of fractions.¹² So you multiply one and five sevenths by twenty-one. This gives you thirty-six, which is the quantity.

[Solution by double false position]And if you wish, work it out by the [method of] scales, which is that you take any number you wish for the front [scale], which you are allowed to do. So you make the front scale three. You take its third and its fourth: it is one and three fourths. Confront it with the twenty-one. You find it is smaller. So you made an error in the “three” scale of nineteen and a fourth falling short, and keep this error in mind.

Then you take the other scale and let it be, for example, four. You take its third and its fourth, and that is two and a third. Confront it with the twenty-one. So you made an error in the “four” scale of eighteen and two thirds falling short.

Multiply the error of the first scale, which is nineteen and a fourth, by the second scale, which is four. That gives seventy-seven. Keep it in mind. Then multiply the error of the second scale, which is eighteen and two thirds, by the first scale, which is three. It gives you fifty-six. Subtract it from the seventy-seven, leaving twenty-one. Then you subtract the smaller of the two errors from the greater. The remainder is three sixths and half of a sixth. Divide the twenty-one by it, giving you thirty-six, which is the quantity itself, and we will clarify this ratio when we get to it.

Footnotes

1

(Ibn al-Bannāʾ 1984, 212.7).

2

The mudy, plural amdāʾ, was a unit of capacity measure (Rebstock 2008). The plural form of Arabic nouns are used for numbers from 3 to 10 only, so fourteen of them are mudy.

3

The dinar (dīnār) was the standard gold coin in Islamicate countries.

4

(Ibn al-Bannāʾ 1984, 206.17).

5

(Ibn Qunfudh manuscript, 297.13).

6

(al-Karajī 1986, 204.8).

7

(ʿAlī al-Sulamī manuscript, fol. 54b.1).

8

The problem is indeterminate, so the author is allowed to pick one of the numbers as he pleases.