Al-Hawārī was not an important mathematician. His only known work, the Essential Commentary on a short book of Ibn al-Bannāʾ, contains no groundbreaking developments nor any original insights. His textbook is simply an introduction to practical arithmetic which enjoyed a modest circulation in the Western part of the Islamic world in late medieval times. And yet this unremarkable book has attracted our interest, and it should attract your interest, too.
The Essential Commentary is worth a modern edition, translation and commentary first of all for what it tells us about the state of Arabic arithmetic in the early fourteenth century. From an historical angle, it is remarkable how techniques and ideas from Greece, the Middle East, and India came to be selected and combined to form such an eclectic whole. Ibn al-Bannāʾ and al-Hawārī were not the first to present shortcuts for mental calculation in a book ostensibly devoted to rules for operating with Indian (i.e., “Arabic”) numerals, and by their time the integration of portions of Greek number theory, from definitions to rules of calculation, was already an established part of arithmetical instruction. The very real tensions created by combining these disparate techniques and ideas could be disregarded by those interested in their utility, and could serve as a starting-points for philosophical discussion by people more interested in theory.
From the conceptual angle, we get to see how the numbers of Arabic arithmeticians differ radically from both Greek and modern numbers. Mathematicians today define real numbers as the elements of a set which, together with binary operations, satisfy the ordered field axioms. Historians of Greek mathematics, for their part, can point to Euclid’s
It is not just the concept of number that differentiates medieval from modern arithmetic. If we pay attention to how Ibn al-Bannāʾ, al-Hawārī, and other authors phrased their explanations and examples, we discover that they expressed them differently, too. Like the numbers in Greek logistic, numbers in Arabic arithmetic were regarded as being numbers of something. Rather than belonging all to the same abstract set, they come in different kinds: a three might be three units (3), three fifths (
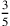 ), three roots of five (a trio of
), three roots of five (a trio of
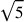 ’s), three cubes (
’s), three cubes (
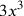 , again a trio), or, in problem-solving, three men or three dirhams. Further, their way of expressing binomials and apotomes, whether of fractions, roots, or algebraic terms, is without parallel in modern arithmetic and algebra. These and other seemingly innocent curiosities of language had a significant impact on how calculations were performed.
, again a trio), or, in problem-solving, three men or three dirhams. Further, their way of expressing binomials and apotomes, whether of fractions, roots, or algebraic terms, is without parallel in modern arithmetic and algebra. These and other seemingly innocent curiosities of language had a significant impact on how calculations were performed.
Becoming familiar with the ways numbers were conceived and expressed is not only interesting in itself, but it provides the necessary background for the study of the works of more brilliant Arabic writers on algebra and arithmetic such as al-Karajī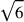 by
by
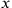 to get
to get
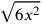 instead of
instead of
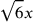 ; and François Viète
; and François Viète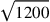 and
and
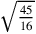 , instead of
, instead of
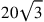 and
and
 .1 These premodern ways of thinking about and expressing numbers and polynomials only truly began to give way with Descartes
.1 These premodern ways of thinking about and expressing numbers and polynomials only truly began to give way with Descartes
Finally, it is worthwhile to actually work through the numerical operations and to solve problems by the methods described in this book. For you adventurous types willing to perform a division of fractions or to work through a problem by double false position, you will leave paper and pencil behind and take up the dust board (a chalkboard will suffice). And by reading aloud the instructions provided by our authors, you can gain some insight into the prominent role played by recitation and memorization in student-teacher interactions. Supplementing notational board calculations with rhetorical presentation not only helps one remember the rules, but it also causes one to think about the meanings of the signs, which, on reflection, ultimately accounts for their curious (to us) ways of expressing arithmetical and algebraic quantities.
We have written this book with different readers in mind, mainly historians of mathematics and related fields, mathematicians, and mathematics educators. Please keep in mind that, for each group, we explain different aspects of al-Hawārī’s book that people in other groups might find too elementary.
This book is divided into five parts. The introduction covers the basic historical, textual, social, and conceptual aspects of Arabic arithmetic that form the backdrop to al-Hawārī’s book. This is followed by our translation of the Essential Commentary. Because books written in another language many centuries ago cannot speak entirely for themselves, we have written a passage-by-passage commentary to al-Hawārī’s commentary which turned out to be longer than the translation itself. Appendices follow, which include a conspectus of problems, sample worked-out problems solved by various methods from other Arabic books, a brief chronological list of ancient and medieval mathematicians and other scholars, and a glossary of Arabic terms. The English portion finishes with the bibliography and an index of names. Last (or first, if you are an Arabic reader) is the corrected critical edition of the Arabic text together with its own introduction and conspectus, which we originally published in Tunisia in 2013.
Each passage of the translation and our commentary is linked to the Arabic edition by a reference to page and line number. For example, “201.14” in the margin of the translation, or in a box in our commentary, refers to page 201, line 14 of the Arabic edition. Cross references are given throughout. For readers who will not consult the original Arabic, these references still serve to link our commentary with the translation. Hyperlinks connect the different parts of the introduction, translation, commentary, and appendices of the online version of this book. We were unable to make hyperlinks with the Arabic part because the English part was typeset in XeLaTeX while the Arabic part was typeset in MSWord.
Most of what we write in the commentary is directed specifically at the passage in question. But many times we offer remarks to clarify the mathematics from a more general point of view, whether mathematical, conceptual, linguistic, or historical. In our comments at 68.18, for example, we pause to give a breakdown of the vocabulary used in the writing of numbers; at 74.14 we devote a page to how zero was dealt with in calculations; and at 219.1 and 219.4, we devote more than five pages to an explanation of how Arabic ways of expressing operations and their results differ from ours, and so on.
Two bio-bibliographic works are indispensable for sorting out details of the works of medieval Arabic mathematicians. B. A. Rosenfeld’s and E. Ihsanoğlu’s 2003 Mathematicians, Astronomers, and Other Scholars of Islamic Civilisation and Their Works (7th-19th c.) lists the names and works of 1,711 scholars known to have written books in the mathematical sciences, and Driss Lamrabet’s 2014 Introduction à l’Histoire des Mathématiques Maghrébines does much the same for 983 scholars who worked in the western part of the Islamic world. References after names are to these two works. For example, for al-Ḥaṣṣār
We follow the International Journal of Middle East Studies system for transliteration of Arabic words.3
It was Mahdi’s idea to write this book. With some input from me, he collected the manuscripts and produced the critical edition. We each then translated the book independently, and I compared the two translations to produce the version you see here. I then wrote the commentary, the introduction, and the appendices, with valuable input from Mahdi.
Finally, we thank Len Berggren, Margaret Gaida, and Robert Morrison for their comments and suggestions on an earlier version of this book.
Jeff Oaks,
Indianapolis, May 4, 2019.
Footnotes
(Stifel 1544, fol. 283a); (Viète 1646, 140, 309). In Stifel’s notation, he multiplies

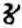 6 by 1
6 by 1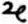 to get
to get
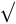
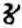 6
6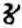 . See (Oaks 2017).
. See (Oaks 2017).
(Oaks 2018b).
