Below is a list of exceptionally brief notices on some of the different mathematicians and philosophers mentioned in this book. References are given to () and () where applicable. For example, for al-Ḥaṣṣār we write (#532, M55), which means that he is scholar #532 in Rosenfeld & Ihsanoğlu, and scholar M55 in Lamrabet. Rosenfeld and Ihsanoğlu give numbered lists of individual titles by each author. For example, “[M2]” after an Arabic title indicates book M2 in their list.
After Aristotle and Euclid all dates are CE, and with a few AH.
Aristotle (384-322 BC). Three aspects of Aristotle’s thought impacted al-Hawārī’s book, most likely through the works of Ibn Sīnā. One is the distinction between quality and quantity at 92.17, another is the distinction between sensible and intelligible objects at 133.3, and the third is the division of the genus of “quantity” into discrete and continuous, discussed in our commentary at 117.2 and 133.3. For a brief overview of Aristotle’s influence on Arabic mathematics, see Section 4 in our introduction.
Euclid (ca. 300 BC). Euclid wrote his Elements in Greek around 300 BC in Alexandria. The work consists of thirteen “Books”, or what we might call long chapters. Books I through VI cover plane geometry, Books VII to IX discuss number theory, the long Book X deals with the theory of quadratic irrationals in a geometric context, and Books XI to XIII deal with three-dimensional geometry.
Euclid’s Elements is reported to have been first translated into Arabic by al-Ḥajjāj ibn Yūsuf ibn Maṭar during the reign of the caliph Hārūn al-Rashīd (786-809). Al-Ḥajjāj later produced a second and improved translation during the reign of al-Maʾmūn (813-833). Later in the century Isḥāq ibn Ḥunayn (830-910) translated the Elements, and this was subsequently revised by Thābit ibn Qurra (836-901). While the surviving manuscripts apparently all derive from Thābit’s version, they also contain passages from al-Ḥajjāj. In addition, quotations from other books preserve parts of the earlier translations. The textual history of Euclid’s Elements in Arabic is complex and at present not well understood.
Euclid’s Data, another work on geometry, was also translated into Arabic and influenced the ways some Arabic mathematicians presented proofs.
The influence of Euclid’s Elements on al-Hawārī’s book is seen in the definitions of “number” (see our commentary at 65.2), “oddly-odd” (66.7), “multiplication” (95.2), “ratio”, “part”, “parts” (133.1), “medial” (163.4), and “ex-aequali” (195.2). The terms “side”, “surface”, and “square” (66.17) also ultimately come from Euclid, as do the various manipulations of ratios covered at 196.16. The entire theory of quadratic irrationals beginning at 173.4 derives from an arithmetical reading of Elements Book X. Some fragments of al-Ḥajjāj’s translation of this book may have found their way into al-Hawārī’s book. See our comments at 173.10.
Nicomachus of Gerasa (fl. second century). Nicomachus was a Neopythagorean philosopher who wrote his Arithmetical Introduction more as a prolegomenon (introduction) to philosophy than as a treatise on mathematics. He devotes the first six chapters to a philosophical argument for the primacy of arithmetic in the mathematical sciences, and he covers aspects of what we would call elementary number theory in the rest of the book. Ḥabīb ibn Bihrīz translated the Arithmetical Introduction into Arabic from a Syriac version shortly before 822. Thābit ibn Qurra translated Nicomachus’s work into Arabic again some decades later, this time directly from the Greek.
Nicomachus’s influence is evident in the definitions of “evenly-even”, etc. (65.10), the distinction between disparities of quantity and quality in sequences (73.7, 73.17), the sieve of Eratosthenes (127.10), and in the list of the kinds of proportion that al-Hawārī copied from Ibn al-Bannāʾ’s Lifting the Veil (195.2).
Diophantus (ca. 300). This Alexandrian mathematician wrote his Arithmetica in thirteen “books”. Six survive in Greek and another four in the Arabic translation of Qusṭā ibn Lūqā. In this work Diophantus solves determinate and indeterminate problems by algebra.
al-Khwārazmī, early ninth century (#41). Muḥammad ibn Mūsā al-Khwārazmī worked in Baghdad and authored works on Indian arithmetic, algebra, astronomy, astrology, geography, and the Jewish calendar. The earliest known books on algebra are al-Khwārazmī’s Book of Algebra (Kitāb al-jabr wa l-muqābala, [M3]) and Ibn Turk’s book by the same title. Only a fragment of the latter is extant, while al-Khwārazmī’s book survives in its entirety. Al-Khwārazmī’s Book on Indian Reckoning (Kitāb al-ḥisāb al-hindī, [M1]) covers the rules of calculating with Arabic numerals, and survives only in a medieval Latin reworking of a Latin translation.
Ibn Turk, early ninth century (#59). The only part of ʿAbd al-Ḥamīd Ibn Turk’s Book of Algebra (Kitāb al-jabr wa l-muqābala, [M1]) that is extant is the part giving proofs for the rules for solving simplified equations.
Thābit ibn Qurra, 836-901 (#103). Abū l-Ḥasan Thābit ibn Qurra al-Ḥarrānī was a prolific translator and scholar who worked in all branches of the mathematical sciences. He revised Isḥāq ibn Ḥunayn’s Arabic translation of Euclid’s Elements, and he translated Nicomachus’s Arithmetical Introduction as well as some works of Archimedes into Arabic.
Among Thābit’s original contributions to mathematics are his calculations of area and volume in the tradition of Archimedes, including the volume of a section of a paraboloid. These are not numerical calculations. Instead, they equate the areas and volumes to other known areas and volumes. Thābit also wrote a short treatise on algebra titled Establishing the Correctness of Algebra Problems by Geometric Proofs (Qawl fī taṣḥīḥ masāʾil al-jabr bi l-barāhīn al-handasiyya, [M19]) in which he proved the rules for solving the three composite quadratic equations in the style of Euclid’s Data.
Qusṭā ibn Lūqā, died ca. 910 (#118). Among the many contributions Qusṭā made to mathematics, the two of interest to the current study are his translation of Diophantus’s Arithmetica and his short treatise in which he proved the rules of double false position via geometry in the style of Euclid’s Data.
Abū Kāmil, late ninth century (#124). Abū Kāmil, whose full name is Shujāʿ ibn Aslam ibn Muḥammad ibn Shujāʿ, is best known for his comprehensive Book on Algebra (Kitāb fī l-jabr wa l-muqābala, [M1]), written as a kind of commentary on al-Khwārazmī’s algebra book. The rules in algebra for finding the māl directly, first mentioned at 214.2 ultimately come from this book.
ʿAlī al-Sulamī, tenth century (#267). This Syrian mathematician is known only for his Sufficient Introduction on Calculation by Algebra and What One Can Learn from its Examples (al-Muqaddima al-kāfiyya fī ḥisāb al-jabr wa l-muqābala wa mā yuʿrafu bihi qiyāsuhū min al-amthila, [M1]), which survives in a single manuscript. The book exhibits borrowings from Abū Kāmil and al-Khwārazmī. His full name is Abū l-Ḥasan ʿAlī ibn al-Muslim ibn Muḥammad ʿAlī al-Fatḥ al-Sulamī.
Ikhwān al-Ṣafāʾ (Brethren of Purity), tenth century (#226). The Brethren of Purity were a group of anonymous mystical scholars centered in the city of Basra. Their highly influential Epistles of the Brethren of Purity (Rasā’il Ikhwān al-Ṣafāʾ, [E1]) is a kind of encyclopedia of all knowledge situated in a universalist philosophical/theological setting. The first of its four parts is on mathematics, where the main influences for arithmetic are the Greek Neopythagoreans, especially Nicomachus, and for geometry Euclid’s Elements.
al-Uqlīdisī, tenth century (#232). Abū l-Ḥasan Aḥmad ibn Ibrāhīm al-Uqlīdisī wrote his Chapters on Indian Arithmetic (al-Fuṣūl fī l-ḥisāb al-Hindī, [M1]) in 952-3. It is the oldest extant Arabic treatise on calculating with Arabic numerals. The nickname “al-Uqlīdisī” can be translated as “the Euclidean”, presumably because he worked on Euclid’s Elements. His book on arithmetic is unrelated to Euclid’s work.
Abū l-Wafāʾ, 940-998 (#256). The earliest extant book dedicated primarily to finger-reckoning is Abū l-Wafāʾ’s Book of What is Necessary for Scribes, Businessmen, and Others in the Science of Arithmetic (Kitāb fīmā yaḥtāju ilayhi al-kuttāb wa l-ʿummāl wa ghayruhum min ʿilm
al-ḥisāb, [M2]), written between 961 and 976. Full name: Abū l-Wafā Muḥammad ibn Muḥammad ibn Yaḥyā ibn Ismāʿīl ibn al-ʿAbbās al-Būzjānī.
al-Karajī, died ca. 1025 (#309). Fakhr al-Dīn Abū Bakr Muḥammad ibn al-Ḥasan (or al-Ḥusayn) al-Karajī was a Persian mathematician and engineer who wrote his works on algebra and arithmetic in Baghdad. His three main works, in chronological order, are:
[Book of] al-Fakhrī on the Art of Algebra (al-Fakhrī fī ṣināʿat al-jabr wa l-muqābala, [M2]). This is al-Karajī’s book on algebra, modeled on Abū Kāmil’s Book on Algebra and Diophantus’s Arithmetica. It was probably completed in 401H/1010-1 CE.
The Sufficient [Book] on Arithmetic (al-Kāfī fī l-ḥisāb, [M1]). A work on calculation by finger-reckoning with a section on algebra. It was probably completed in 402H.
Marvelous [Book] of Arithmetic (al-Badīʿ fī l-ḥisāb, [M3]). This book covers various techniques of calculation, beginning with an introduction to arithmetic based in Euclid and Nicomachus, then a section on algebra, and ending with an exposition on techniques of solving indeterminate problems by algebra.
Kūshyār ibn Labbān, ca. 970-1030 (#308). Kūshyār was a Persian mathematician and astronomer who wrote a book on calculating with Arabic numerals, titled Principles of Indian Reckoning (Kitāb fī uṣūl ḥisāb al-Hindī, [M1]). Full name: Abū l-Ḥasan Kūshyār ibn Labbān ibn Bāshahrī al-Jīlī.
Ibn Sīnā, ca. 970-1037 (#317). Abū ʿAlī al-Ḥusayn ibn ʿAbdallāh ibn Sīnā, known in Latin as Avicenna, was the most important philosopher of medieval Islam. He was second only to Aristotle in influence in the Islamic world and in the late medieval and early modern West. For epistemology and ontology he built on the works of Aristotle, and it is most likely through him that Aristotelian ideas are present in al-Hawārī’s book.
al-Baghdādī, died 1038 (#320). Abū Manṣūr ʿAbd al-Qāhir ibn Ṭāhir al-Baghdādī was a Persian mathematician and judge best known for his Completion of Arithmetic (al-Takmila fī l-ḥisāb, [M1]). This book covers calculation with Indian numerals on the dust-board, sexagesimal arithmetic, number theory, and business arithmetic.
Ibn al-Samḥ, early eleventh century (A93). Abū l-Qāsim Aṣbagh ibn Muḥammad ibn Aṣbagh ibn al-Samḥ was a mathematician, astronomer, and physician who taught in Grenada. His Sufficient Book on Mental Reckoning (Risāla kāfiya fī ʿilm al-ḥisāb) covers techniques of finger-reckoning and double false position.
Ibn al-Haytham, 965-1041 (#328). Known also by his Latinized name Alhazen, Ibn ʿAlī al-Ḥasan ibn al-Ḥasan ibn al-Haytham is best known for his groundbreaking work in optics. What interests us is his short work The Arithmetic of Transactions (Ḥisāb al-muʿāmalāt, [M24]). It was common for scientists conducting advanced work to produce elementary texts like this. Naṣīr al-Dīn al-Ṭūsī (below) is another.
al-Bīrūnī, 973-1048 (#348). Abū l-Rayḥān Muḥammad ibn Aḥmad al-Bīrūnī wrote extensively on a wide range of topics including anthropology, linguistics, natural science, mathematics, and astronomy. Book II of his Book of Instruction in the Elements of the Art of Astrology (Kitāb al-tafhīm li-awāʾil ṣināʿat al-tanjīm, [A2]) covers arithmetic. The first part, on number theory (pp. 72-95), is largely taken from Nicomachus, with some influence from Indian sources. The second part (pp. 96-119) covers calculation: multiplication, division, roots, sexagesimal and base ten arithmetic, algebra, double false position, and abjad calculation.
al-Qurashī, 1030-1067. Abū l-Ḥasan ʿAlī ibn al-Khiḍr al-Qurashī hailed from Syria. His Note on the Elements of Calculation and Inheritance (al-Tadhkira bi-uṣūl al-ḥisāb wa l-farāʾiḍ) is a summary of his more extensive, and lost, Book of Sustenance (Kitāb al-Maʿūna). It covers practical arithmetic, with a focus on the division of estates.
al-Khayyām, 1048-1131 (#420). Better known in the West as Omar Khayyam, Ghiyāth al-Dīn Abū l-Fatḥ ʿUmar ibn Ibrāhīm al-Khayyāmī (Khayyām) was a poet, mathematician, and astronomer best known to historians of mathematics for his Treatise on the Proofs of Algebra Problems (Risāla fī l-barāhīn ʿalā masāʾil al-jabr wa l-muqābala, [M2]), in which he classifies and solves the twenty-five equations of degree three and less. Al-Khayyām saw algebra as a tool for geometric problem-solving, so he gives constructions for solving each equation type. He also gave numerical solutions where he could, but rules for solving irreducible cubic equations would not be found until the sixteenth century. Al-Khayyām was able to justify the appropriation of algebra for solving problems in geometry by regarding the numbers of the algebraists as the dimensionless measures of continuous magnitudes.
al-Samawʾal, died ca. 1175 (#487). Al-Samaw-al ibn Yaḥyā ibn ʿAbbās al-Maghribī was a native of Baghdad who later worked in Iran. He built on the works of al-Karajī and others to develop computational rules for polynomials (“composite numbers”) in his The Dazzling [Book] on the Science of Calculation (al-Bāhir fī ,ilm al-ḥisāb, [M1]).
al-Ḥaṣṣār, died before 1194 (#532, M55). Abū Bakr Muḥammad ibn ʿAbdallah ibn ʿAyyāsh al-Ḥaṣṣār’s Book of Demonstration and Recollection in the Art of Dust-Board Reckoning (Kitāb al-bayān wa l-tadhkār fī ṣanʿat ʿamal al-ghubār, [M1]) is the earliest extant Arabic book showing the notation of fractions with the division bar, among other innovations. He also wrote a more comprehensive book on arithmetic, the Complete [Book] on the Art of Number (al-Kāmil fī ṣināʿa al-ʿadad, [M2]). Al-Ḥaṣṣār worked in al-Andalus and Morocco.
Ibn al-Yāsamīn, died 1204 (#521, M83). Originally from Fez in Morocco, Abū Muḥammad ʿAbdallah ibn Muḥammad ibn Hajjāj ibn al-Yāsamīn al-Adrīnī composed his Grafting of Opinions of the Work on Dust Figures (Talqīḥ al-afkār fī l-ʿilm bi-rushūm al-ghubār, [M3]) in Seville. This book is a hybrid between a textbook on Indian arithmetic and one on finger reckoning. It is the earliest book we know to show the Arabic algebraic notation, though it is clear by the way he presents it that it was not his invention. Ibn al-Yāsamīn is also well known for his 54-line Poem on Algebra (Urjūza fī l-jabr, [M1]), which inspired as many commentaries as Ibn al-Bannāʾ’s Condensed Book.
Ibn al-Bannāʾ copied many parts of Ibn al-Yāsamīn’s Grafting of Opinions nearly word-for-word into his Condensed Book. Much of the chapter on the addition of whole numbers (73.2 through 79.13), the paragraph on multiplication at 98.4, the rules (mostly) from finger-reckoning from 109.7 through 114.4 (except 113.6), and the first couple of sentences on division at 117.2-5 were taken from it.
Ibn Munʿim, twelfth-thirteenth centuries (#556, M89). Abū Jaʿfar Aḥmad ibn Ibrāhīm ibn Munʿim al-ʿAbdarī was a Moroccan mathematician who wrote his book Understanding Calculation (Fiqh al-ḥisāb, [M1]) at a more theoretical level than the textbooks of people like al-Ḥaṣṣār or Ibn al-Yāsamīn.
Ibn Fallūs, 1194-1239 (#584). Shams al-Dīn Abū l-Ṭāhir Ismāʿīl ibn Ibrāhīm ibn Ghāzī al-Māridīnī was known by the name Ibn Fallūs. It was during a pilgrimage to Mecca that he wrote his treatise on algebra with a rhyming title: Kitāb niṣāb al-ḥabr fī ḥisāb al-jabr (Preparation for writing on calculation in algebra, [M3]). He also wrote a textbook on finger-reckoning, Direction to Reckoners Showing the Right Path in Revealing the Science of Arithmetic (Irshād al-ḥussāb fī al-maftūḥ min ʿilm al-ḥisāb, [M2]).
Ibn Badr, ca. thirteenth century (#587). Abū ʿAbdallah Muḥammad ibn ʿUmar Ibn Badr al-Balansī wrote his Brief Book on Algebra (Kitāb fīhi ikhtiṣār al-jabr wa l-muqābala, [M1]) with borrowings from Abū Kāmil and al-Khwārazmī.
Naṣīr al-Dīn al-Ṭūsī, 1201-1274 (#606). One of the most prolific scholars of medieval Islam, Naṣīr al-Dīn Abū Jaʿfar Muḥammad ibn Muḥammad al-Ṭūsī wrote on philosophy, theology, and a variety of scientific topics. In the sciences he is best known for his work on planetary astronomy, but we are more interested in his relatively insignificant textbook Gathering of Arithmetic by Means of Board and Dust (Jāmiʿ al-ḥisāb bi l-takht wa l-turāb, [M17]).
al-Fārisī, died 1319 (#674). Kamāl al-Dīn al-Fārisī was a Persian mathematician who wrote his scientific examination of the rules of finger reckoning, Foundation of the Rules on Elements of Benefits (Asās al-qawāʿid fī uṣūl al-fawāʾid, [M2]), in the form of a commentary on a textbook of his teacher Ibn al-Khawwām.
Ibn al-Bannāʾ, 1256-1321 (#696, M134). See section 1 in the Introduction for bio-bibliographic details.
al-Hawārī, early fourteenth century (#747, M148, M150). See section 1 in the Introduction for bio-bibliographic details.
Ibn Qunfudh, 1339-1407 (#780, M193). Abū l-ʿAbbās Aḥmad ibn Ḥasan ibn ʿAlī ibn al-Khaṭīb ibn Qunfudh al-Qustantīnī completed his commentary on Ibn al-Bannāʾ’s Condensed Book, titled Lowering the Veil from the Faces of Arithmetical Operations (Ḥaṭṭ al-niqāb ʿan wujūh aʿmāl al-ḥisāb, [M1]), in 1370. He also wrote Foundations for Beginning the Commentary on Ibn al-Yāsamīn’s Poem (on algebra) (Mabādīʾ al-sālikīn fī sharḥ urjūzat Ibn al-Yāsamīn). Both books show the Arabic algebraic notation.
al-Mawāḥidī, second half of the fourteenth century (M176). Abū ʿAbd al-Raḥmān Yaʿqūb ibn Ayyūb al-Mawāḥidī al-Jazūlī wrote the popular commentary titled Achieving the Desire of Commenting on Ibn al-Bannāʾ’s Condensed [Book] (Taḥṣīl al-munā fı sharḥ Talkhīṣ Ibn al-Bannāʾ), ca. 1382.
al-ʿUqbānī, died 1408 (#781, M195). Abū ʿUthmān Saʿīd ibn Muḥammad al-Tujībī al-Tilimsānī al-ʿUqbānī wrote his Commentary on the Condensed [Book] (Sharḥ al-Talkhīṣ) with a focus on providing Euclidean-style proofs to the rules in Ibn al-Bannāʾ’s book. He was a native of Tlemcen, and spend his career between cities now located in Algeria and Morocco.
al-Ḥanbalī, died 1409 (#782). Taqī al-Dīn ibn ʿIzz al-Dīn al-Ḥanbalī copied numerical examples from al-Hawārī’s book into his own Commentary on the Condensed [Book] (Sharḥ al-Talkhīṣ).
Ibn al-Hāʾim, ca. 1355-1412 (#783). Abū l-ʿAbbās Shihāb al-Dīn Aḥmad ibn Muḥammad ibn Imād al-Dīn ibn ʿAlī was known by the name Ibn al-Hāʾim. Among his many books on arithmetic and algebra are his 1387 Commentary on the Poem of al-Yāsamīn (Sharḥ al-Urjūza al-Yāsmīnīyya, [M13]), his 1389 Guidebook for the Science of Aerial Calculation (al-Maʿūnah fī ʿilm al-ḥisāb al-hawāʾī, [M1]), and his Abridgement [of the] Condensed [Book] of Ibn al-Bannāʾ (Mukhtaṣar Talkhīṣ Ibn al-Bannāʾ, [M17]).
al-Kāshī, died 1429 (#802). Giyāth al-Dīn Jamshīd ibn Masʿūd al-Kāshī (or al-Kāshānī) was a mathematician and astronomer in the court of Ulugh Beg in Samarqand. He is best known for his work in planetary astronomy and for his calculations of
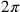 and the sine of one degree, each accurate to the equivalent of 16 decimal places. What interests us is his 1427 book Key to Calculation (Miftāḥ al-ḥisāb, [M1]).
and the sine of one degree, each accurate to the equivalent of 16 decimal places. What interests us is his 1427 book Key to Calculation (Miftāḥ al-ḥisāb, [M1]).
Ibn al-Maghribī, fifteenth century (#910). We mention his Poem on Reckoning with Finger-Joints (Manẓūma fī l-ḥisāb al-ʿuqūd, [M1]) in our Introduction. His full name is Abū l-Ḥasan ʿAlī ibn al-Maghribī.
al-Qalaṣādī, died 1486 (#865, M229). Abū l-Ḥasan ʿAlī ibn Muḥammad al-Qurashī al-Basṭī al-Qalaṣādī was a native of Baza in al-Andalus. His Commentary on the Condensed [Book] on the Operations of Arithmetic (Sharḥ Talkhīs aʿmāl al-Ḥisāb, [M7]) shows the Arabic algebraic notation.
Sibṭ al-Māridīnī, 1423-1506 (#873). Muḥammad ibn Muḥammad ibn Aḥmad Abū ʿAbdallah Badr [Shams] al-Dīn al-Miṣrī al-Dimashqī was the timekeeper at the al-Azhar mosque in Cairo, and authored dozens of works on arithmetic and astronomy. We cite two works in particular: his Student’s Guide to the Way of Arithmetic (Irshād al-ṭullāb ilā wasīlat al-ḥisāb, [M7]) and The Light of al-Māridīnī on Commentary on Ibn al-Yāsamīn (al-Lamʿah al-Māridīnīyah fī sharḥ al-Yāsamīnīyah, [M10]).
Ibn Ghāzī, 1437-1513 (#913, M246). Abū ʿAbdallah Muḥammad ibn Aḥmad ibn Muḥammad Ibn Ghāzī al-ʿUthmānī al-Miknāsī al-Fāsī further condensed Ibn al-Bannāʾ’s Condensed Book into a 461-line poem titled Desire of Reckoners (Munyat al-ḥussāb, [M1]). Later, in 1483, he wrote a commentary on his poem titled Aim of the Students in Commentary on Desire of Reckoners (Bughyat al-ṭullāb fī sharḥ munyat al-ḥussāb, [M2]). This book shows the Arabic algebraic notation, including an entire worked-out problem.
Luca Pacioli, ca. 1446-1517. Italian Renaissance author whose massive, printed, and highly influential 1494 Summa de Arithmetica Geometria Proportioni & Proportionalita presents most of the mathematical knowledge of his time. Much of it ultimately comes from Arabic sources, often via Fibonacci.
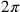 and the sine of one degree, each accurate to the equivalent of 16 decimal places. What interests us is his 1427 book Key to Calculation (Miftāḥ al-ḥisāb, [M1]).35
and the sine of one degree, each accurate to the equivalent of 16 decimal places. What interests us is his 1427 book Key to Calculation (Miftāḥ al-ḥisāb, [M1]).35