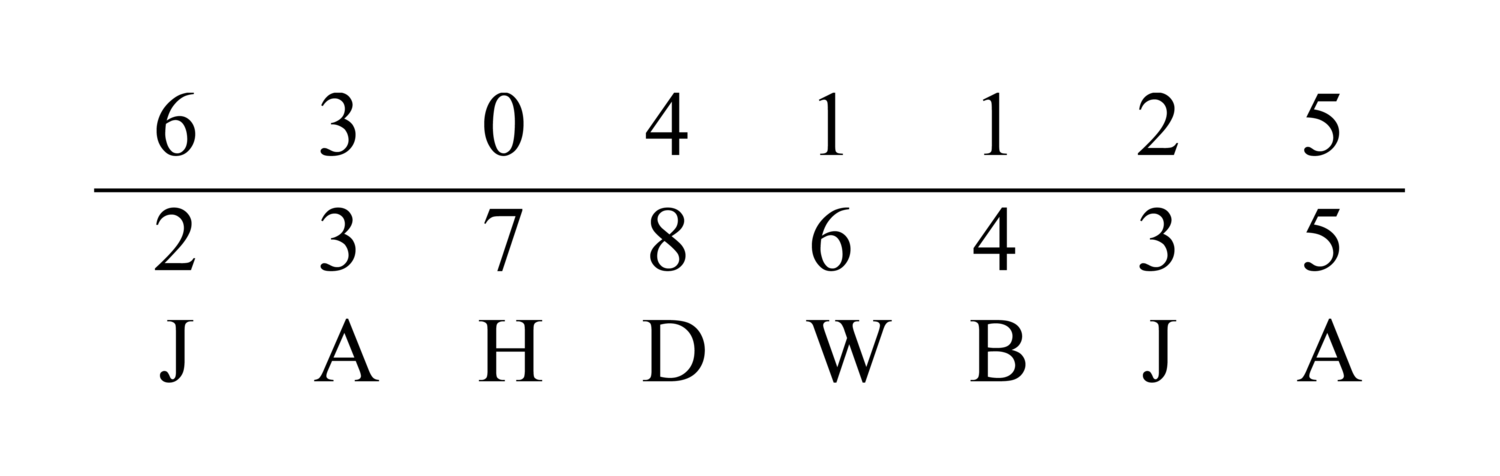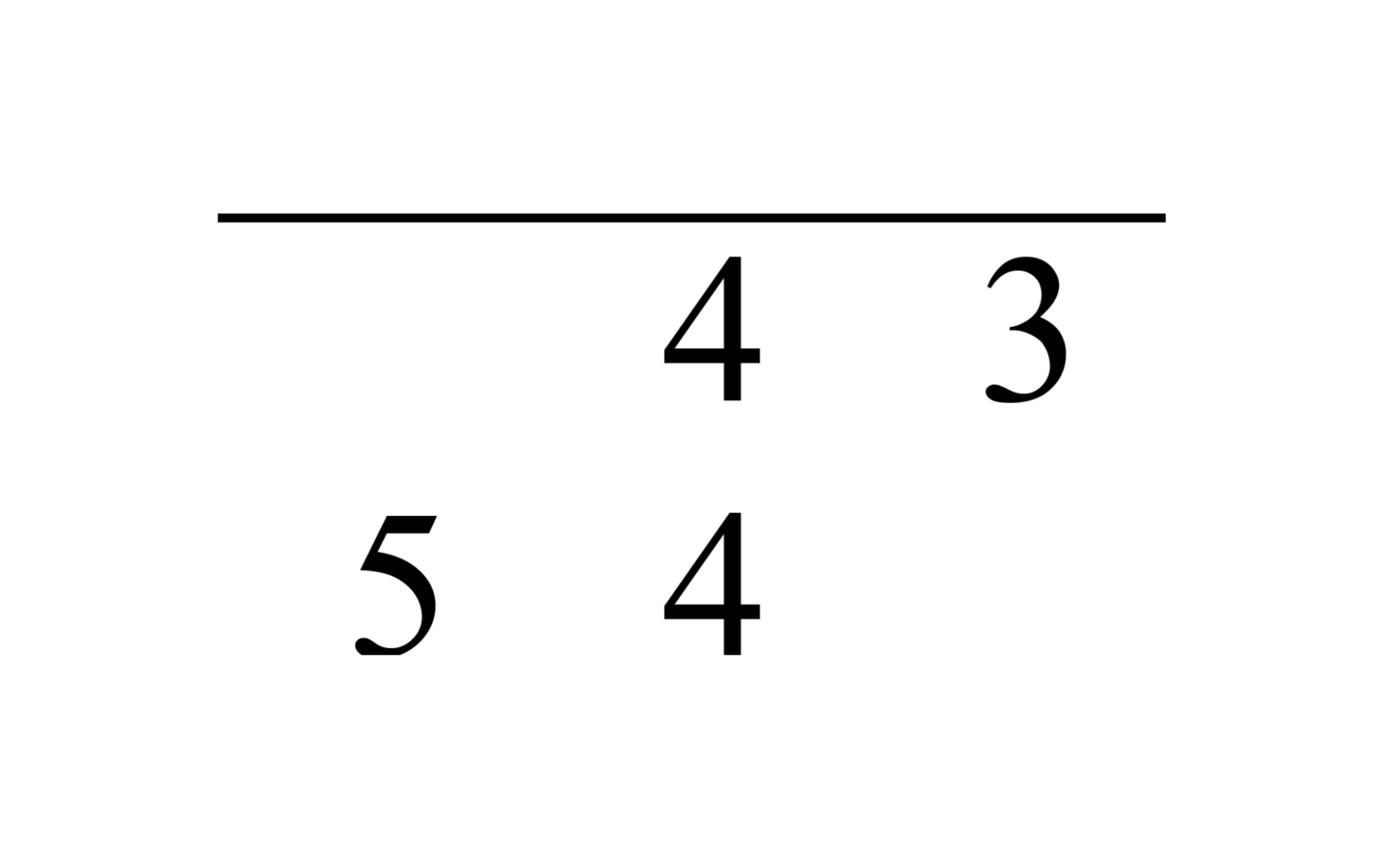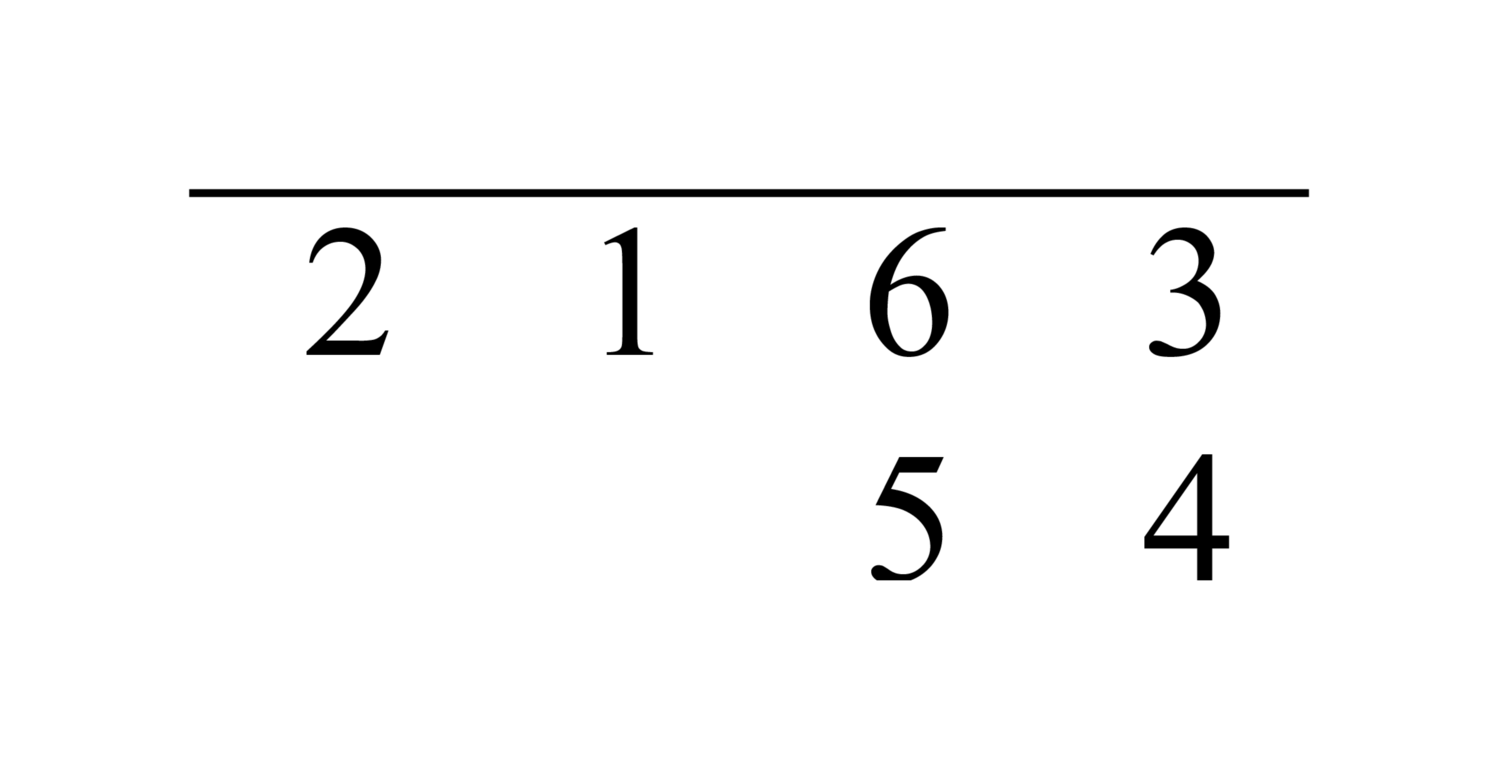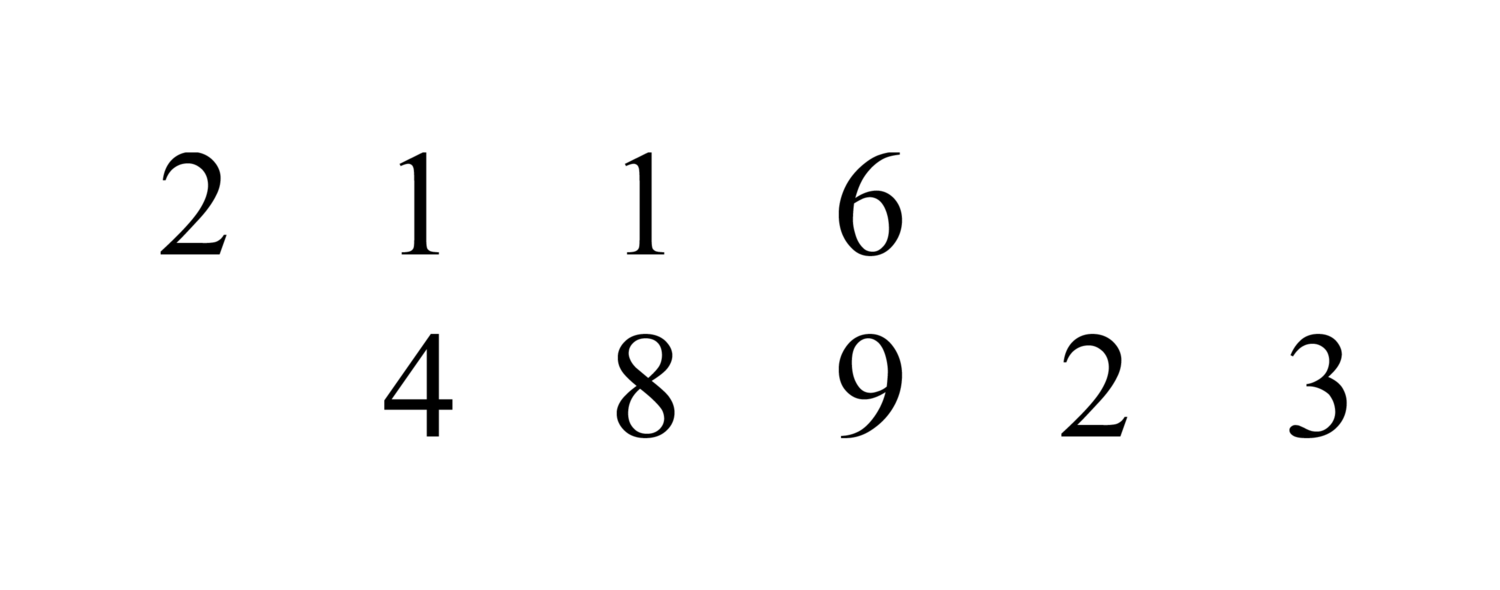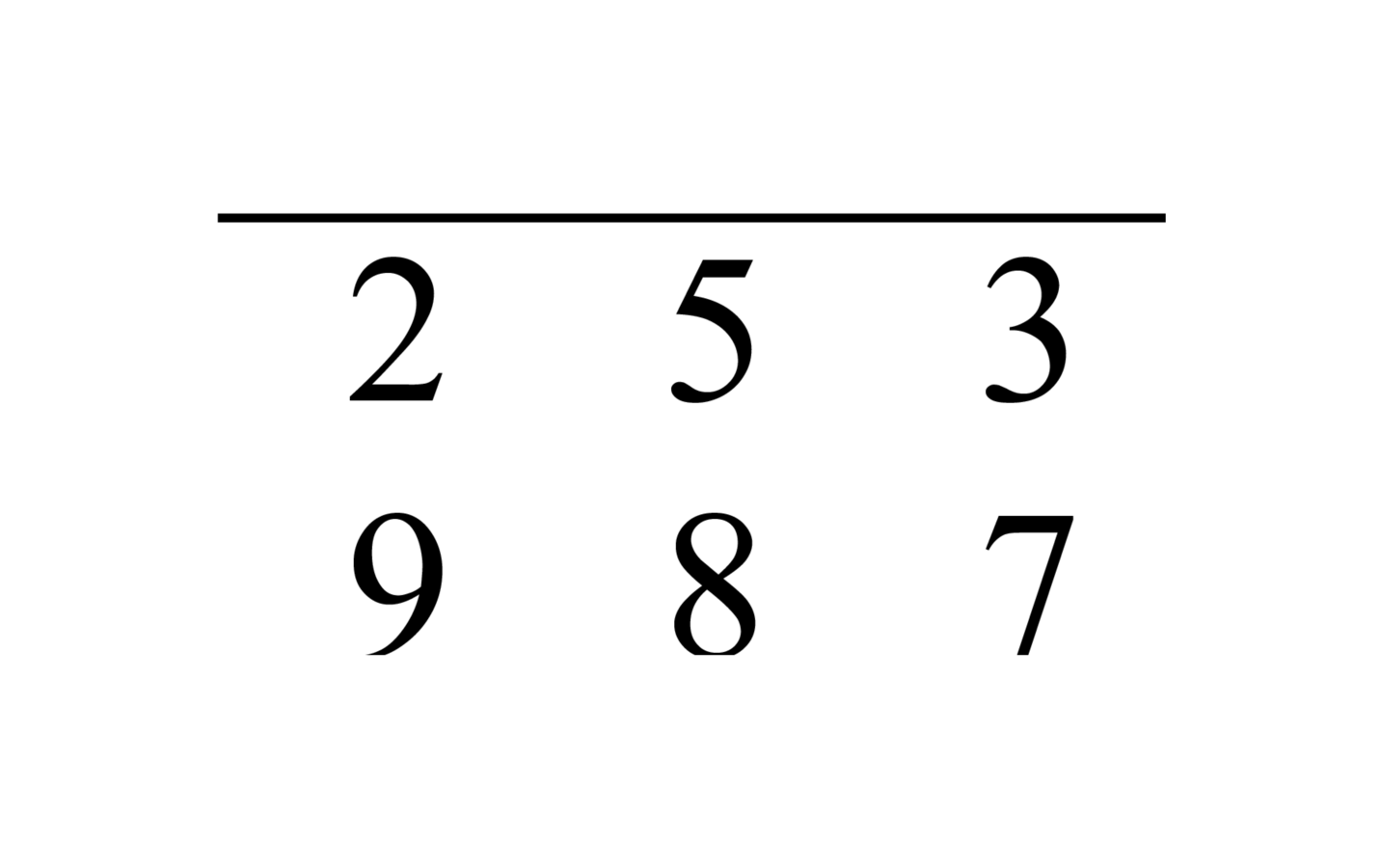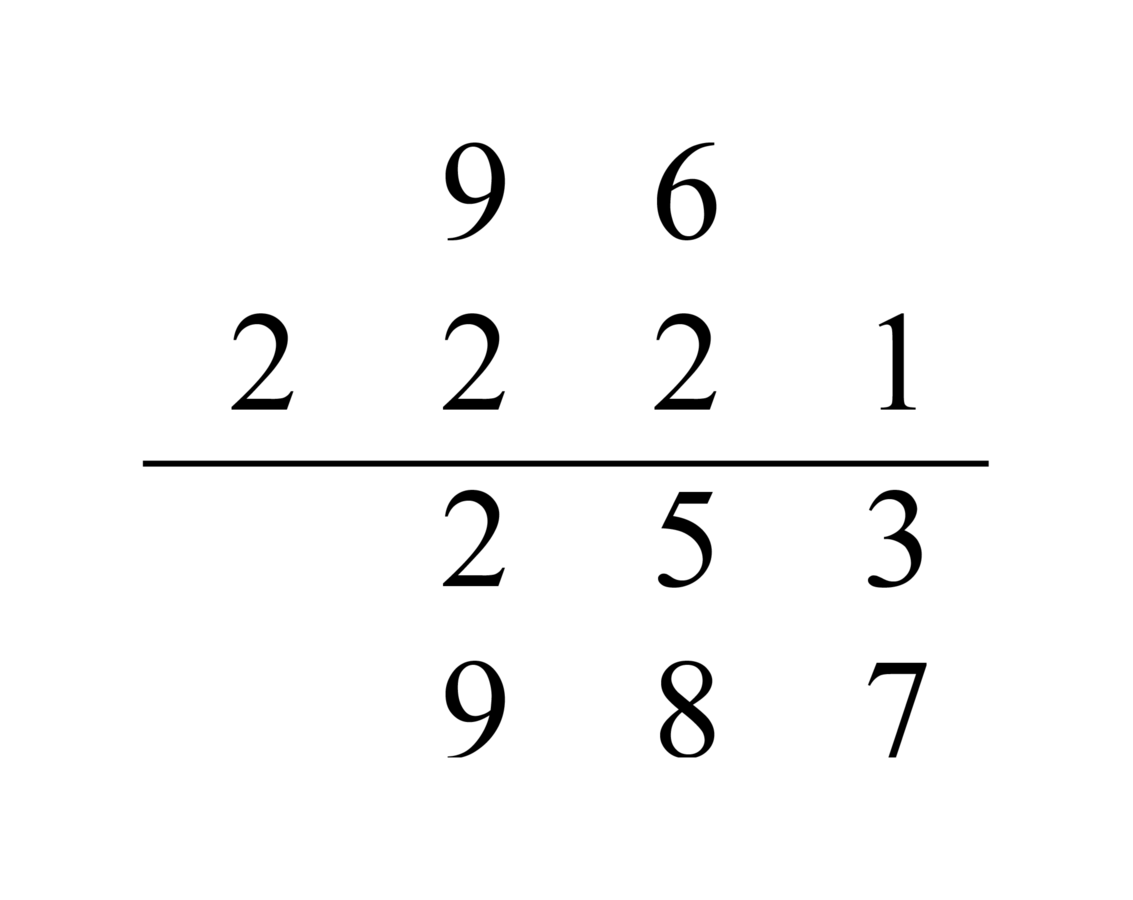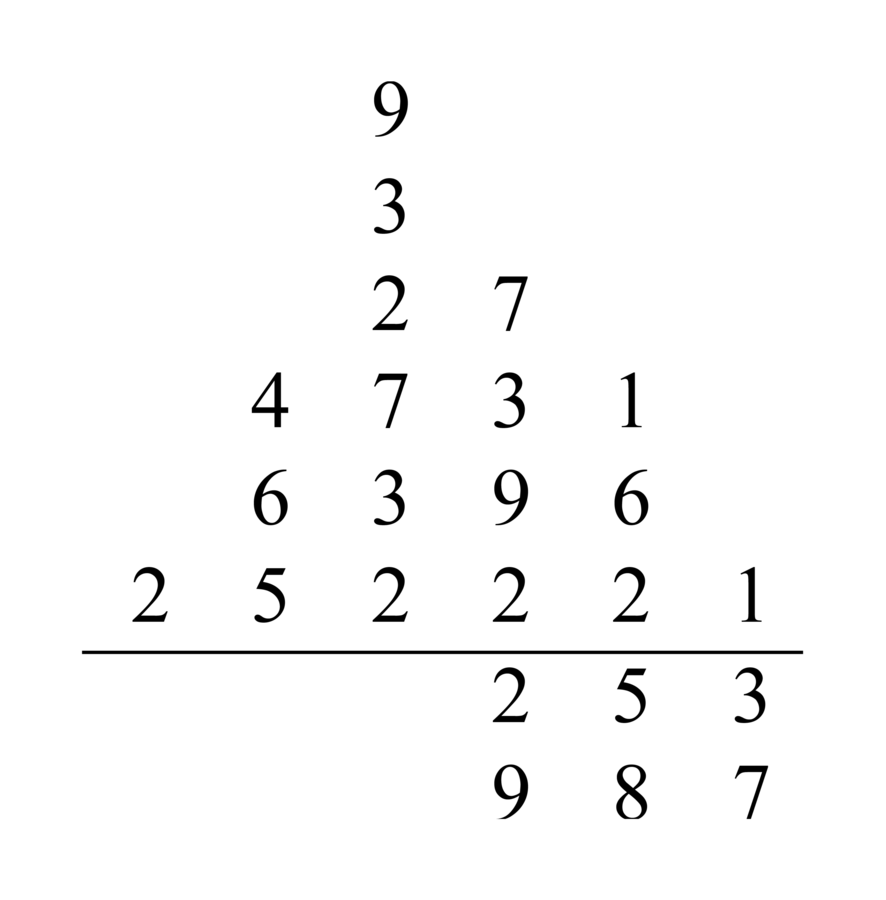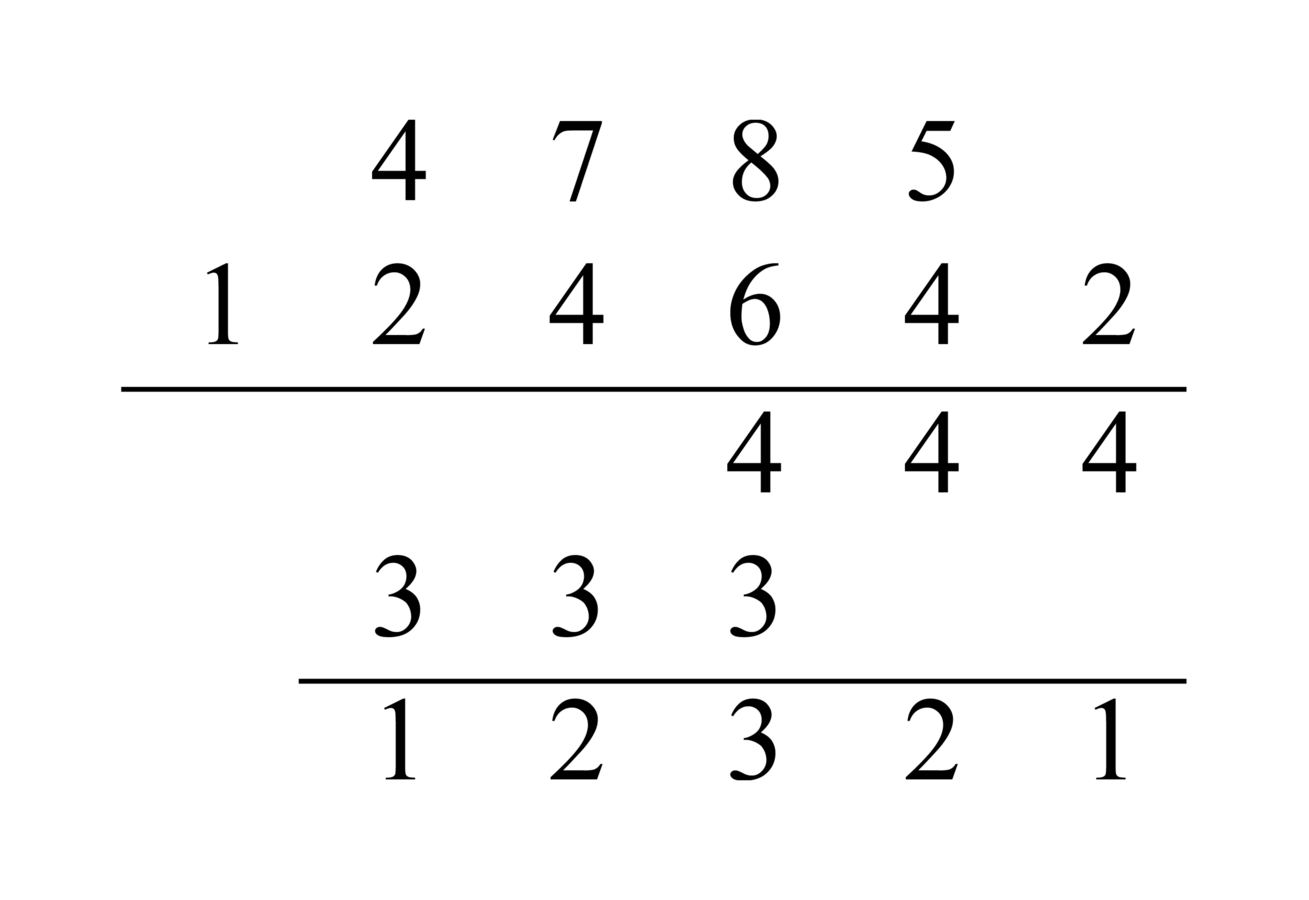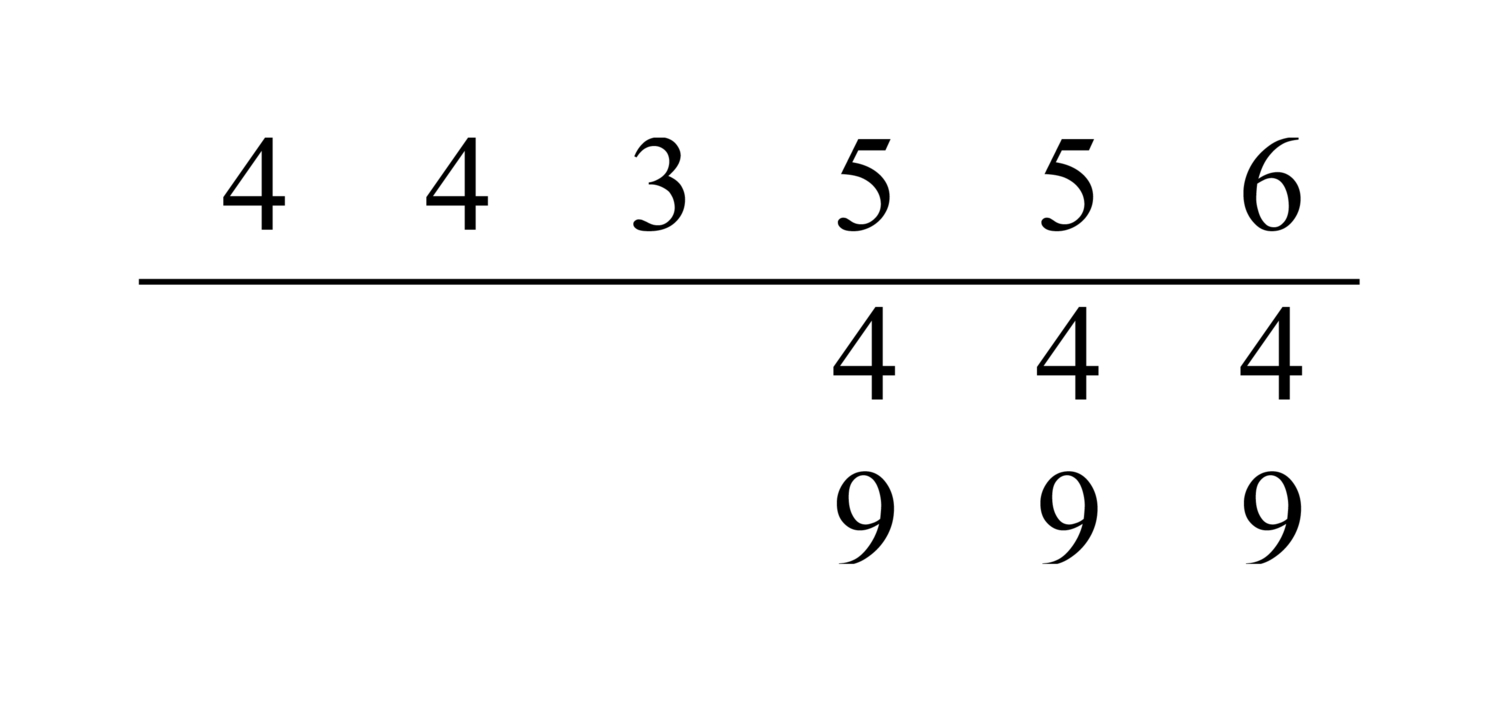Note: The Istanbul and Tunis manuscripts differentiate between passages attributed to Ibn al-Bannāʾ and those attributed to al-Hawārī, while the other three manuscripts we consulted do not make this distinction. In our translation, passages attributed to Ibn al-Bannāʾ that are taken from his Condensed Book are in bold font, while passages attributed to al-Hawārī are not in bold font. Passages borrowed from Ibn al-Bannāʾ’s Lifting the Veil, often with minor changes in wording, are in italics: bold italics for those attributed to Ibn al-Bannāʾ, and regular italics for those attributed to al-Hawārī. Passages attributed to Ibn al-Bannāʾ that are neither in the Condensed Book nor in Lifting the Veil are in small caps. Words and phrases added by us to b make the meaning clearer are placed in [square brackets]. Arabic words behind our translation are placed in parentheses, like “cube (mukaʿʿab)”.
59.1 In the name of God, the Merciful and Compassionate, the humble and submissive servant to his Lord, hoping for His reward and His pardon for his sin, ʿAbd al-ʿAzīz ibn ʿAlī ibn Dawūd al-Hawārī al-Miṣrātī – may God forgive him – said: Praise be to God, the provider of graces and creator of life, who brings things into existence from nothingness, with praises the counting of which is uninterrupted. And full prayers on Muḥammad, His prophet and servant, and for His acceptance of the ancestors, who followed the revealed sunnas while not overstepping their boundary. And a prayer of supplication to our lord, the Commander of the Muslims, son of the Commander of the Muslims, Abū Yaʿqūb,
59.15 I begged almighty God to help me in my task of commenting on the book named Condensed Operations in Arithmetic, written by the incomparable scholar, our most eminent and open-minded master, Sheikh Abū l-ʿAbbās Aḥmad ibn Muḥammad ibn ʿUthmān al-Azdī, may God continue to bestow his divine blessing, care, and grace on him. I enhance my work with your name and embellish it with the splendor of your merits, so that I may deserve your blessing and your protection. To this end I asked our above-mentioned master, the scholar Abū l-ʿAbbās, for permission to undertake this work, to which request he kindly assented. Since the book I undertake to comment on has already been enriched by its own author, God bless him, with Lifting the Veil, containing all that is needed but providing only a few examples, I shall, almighty God willing, illustrate them with examples in the right place and when necessary. I call it the Essential Commentary on the Condensed [Book] on the Operations of Arithmetic. With God’s help and assistance in all circumstances, it is time for me to begin the work, imploring the Almighty to guide and bless my endeavor.
61.1 Our Master, the jurisprudent, the teacher, the leader, the learned, the radiant, the all-knowing, the guardian [of religion], Abū Aḥmad ibn Muḥammad ibn ʿUthmān al-Azdī, may God forgive him, said:
61.9 Part One, on known numbers, which is divided into three chapters. The first is on working with whole numbers, the second on working with fractions, and the third on working with roots.
63.1 Chapter One, on whole numbers. For our purpose, this chapter is divided into six sections.
65.1 Section One, on the divisions of numbers and their ranks.
65.2 A number is a collection of units, and it is divided according to how it is produced into two kinds: whole and fractional. Examples of whole numbers are fifteen, eighteen, and the like. Examples of fractions are a half, three eighths and half an eighth, a ninth and a fourth, six sevenths of seven eighths, and five sixths less a ninth.
65.6 Whole numbers come in two varieties: even and odd. An even number begins with a two or a four or a six or an eight, or does not begin with units, such as ten or fifty or the like. An odd number begins with a one or a three or a five or a seven or a nine.
65.10 Even numbers come in three species: evenly-even, evenly-odd, and evenly-evenly-odd. As for the evenly-even number, it is any number that can be halved, and each of its halves can be halved, until the halving reaches one. For example: thirty-two can be halved, and its half is sixteen. And each of the sixteens can be halved, and its half is eight. Half of the eight is four, half of the four is two, and half of the two is one, and the same for similar examples.
66.7 Odd numbers come in two species: prime and oddly-odd. As for the odd prime number, it is any number that cannot be counted except by one, like eleven and twenty-nine and the like. They are also called deaf parts or simple, which will become clear in the work on the sieve.1 As for the oddly-odd number, it is any number that can be counted by odd numbers, like fifteen, which is composed from the product of three by five. The same for similar examples.
66.13 I say we need to provide here an introduction in which we mention the names of the composite numbers according to their differences, and we will give examples of them. We say that the number, in relation to its composition, is either even or odd. Even numbers come in two varieties, either non-composite simple prime, which is uniquely two, or composite, which are of three kinds.
66.17 The composition of two equal numbers is called a square, or a number that has a root, and each of the two numbers is called a side or a root. For example, thirty-six is composed from six by six. The whole thirty-six is called a square or a number that has a root. Each of the sixes is called a side or a root.
67.12 And the composition of three equal numbers is called a cube, and each of these numbers is a side and a cube root. For example, sixty-four is composed from the product of four by four by four. The whole sixty-four is called a cube, and each of these fours is called a side or a cube root. Likewise for similar situations. Some call the cube (mukaʿʿab) a cube root (kaʿb), which is a name for its side.
68.11 Subsection. The side and the cube root have come to have the same meaning, just as the root and the side also have the same meaning. They differ only as general and particular [substances] differ formally, but they are equal in usage. Taking a side of the cube2 is a lengthy work of little benefit, which is why he3 did not mention it, may God be satisfied with him. However, it can be found by means of decomposition, which is easy. You decompose the cube into the numbers of which it is composed. With them, you piece together three equal numbers by composition such that one of them is the required side. Study this with attention. You shall attain your aim, by God’s will.
68.18 As numbers increase indefinitely, they are placed in three ranks. They are called ranks because one of them follows another, and the units in each rank are greater than the units that came before them and smaller than the units that follow.4 They are also called places, because the number resides in them. The places of each number repeat periodically.
69.2 In each rank are nine numbers. The first rank consists of one to nine, and is called the units rank. Their figures are 1, 2, 3, 4, 5, 6, 7, 8, 9. Someone has written a poem about them:
Alif and ḥā then ḥajja followed by ʿuw
and after the ʿuw by an ʿayn. Draw
Hā followed by a distinct figure
looking like an anchor, and also you position
Two zeros for eight with an alif [between them]
and wāw is the ninth [digit]; so understand it.
70.2 And of the fourth rank, which is the thousands, we say: units, tens, hundreds, which all are thousands, and together they differ with the first three ranks only by the word “thousands”. Likewise for the three third ranks, which are thousands of thousands: they are also units and tens and hundreds, and differ with the preceding only by the word “thousand” twice. And likewise for the three fourth ranks, which [differ] with the preceding according to the previous description. And likewise for succeeding numbers. So know it.
70.8 For example,6 five and twenty and two hundred and four and eighty thousands and a hundred thousands and seven and sixty thousands thousands and three hundred thousands thousands and nine thousands thousands thousands, and its figure is 9367184225. The four and eighty thousands and the hundred thousands are the units, tens, and hundreds like the first three ranks, differing only by the particular word “thousands”. Likewise, the seven and sixty thousands thousands and three hundred thousands thousands are units, tens, and hundreds, and they vary from the preceding in being thousands of thousands. Likewise for the nine thousands thousands thousands. They are units, tens, and hundreds,7 which differ from the preceding only by the repetition of “thousands” three times. So know it.
71.12 Subsection on knowing the index of the repeated number.8
72.1 Conversely, if you have a great many places and you want its name, then divide it by three. The division leaves you with three or less. The quotient is the number of repetitions of the number obtained in the remainder.
73.1 Section two, on addition.
73.2 Addition is the joining of numbers one to the other in order to express them with one expression. This is divided into five types. One of them is addition with no known relation, and the second is addition with a known disparity10, which are divided into two kinds.
73.7 [The first is] a disparity in quality, which occurs when the numbers are in geometric progression. The disparity of the numbers consists of different numbers which are equal in quality in the sense that the ratio of one number to the next is equal to the ratio of a half or a third or something else.11 This kind comes in two types, since the ratio can either be the ratio of a half, which is what he means when he says “addition with a disparity like that of the squares of the chessboard and similar [problems]”,12 where the one in the first square is half of the two in the second square, and the two is half of the four in the third square, and so on to the end; or the ratio can be a third or a fourth or a seventh or any other ratio, which is what he means when he says “if the numbers have another disparity”.13 Examples of these will be presented later, almighty God willing.
73.17 The second kind is a disparity in quantity, in which the numbers are in arithmetic progression, such as consecutive numbers with a disparity of one, or consecutive odd numbers with a disparity of two, and the like. So the numbers differ by equal numbers, and it is a difference in quality when considered as the ratio of one number to the next.14 This is what he means when he says “If the disparity of the numbers is a known number other than doubling”.15 He, may God be satisfied with him, said “known disparity” and not “known relation” because whenever the word “relation” is uttered, it suggests the well-known geometric [progression].16
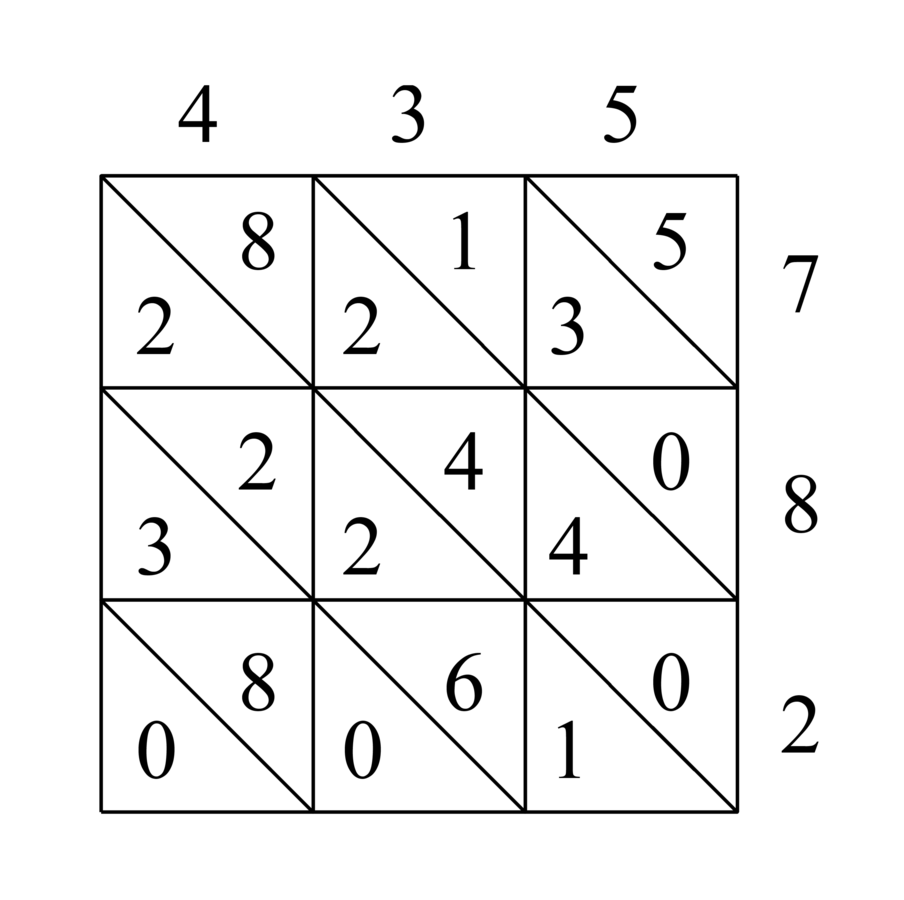
74.17 Here is an example of adding from the first digit. Suppose we want to add four thousand forty-three to two thousand six hundred eighty-five. We write the addend on a line and the augend below it on another line parallel to it, as mentioned, as in this figure:
![\begin{matrix}4043\\[-.5mm]2685\end{matrix}](../../../media/sources/14/4/EOAineq_4_1.png) .
.
75.9 Here is another example, adding from the last rank. Suppose we want to add nine hundred seventy-eight to four hundred fifty-six. We put them down on two lines, as mentioned, as in this figure:
![\begin{matrix}978\\[-.5mm]456\end{matrix}](../../../media/sources/14/4/EOAineq_4_2.png) .
.
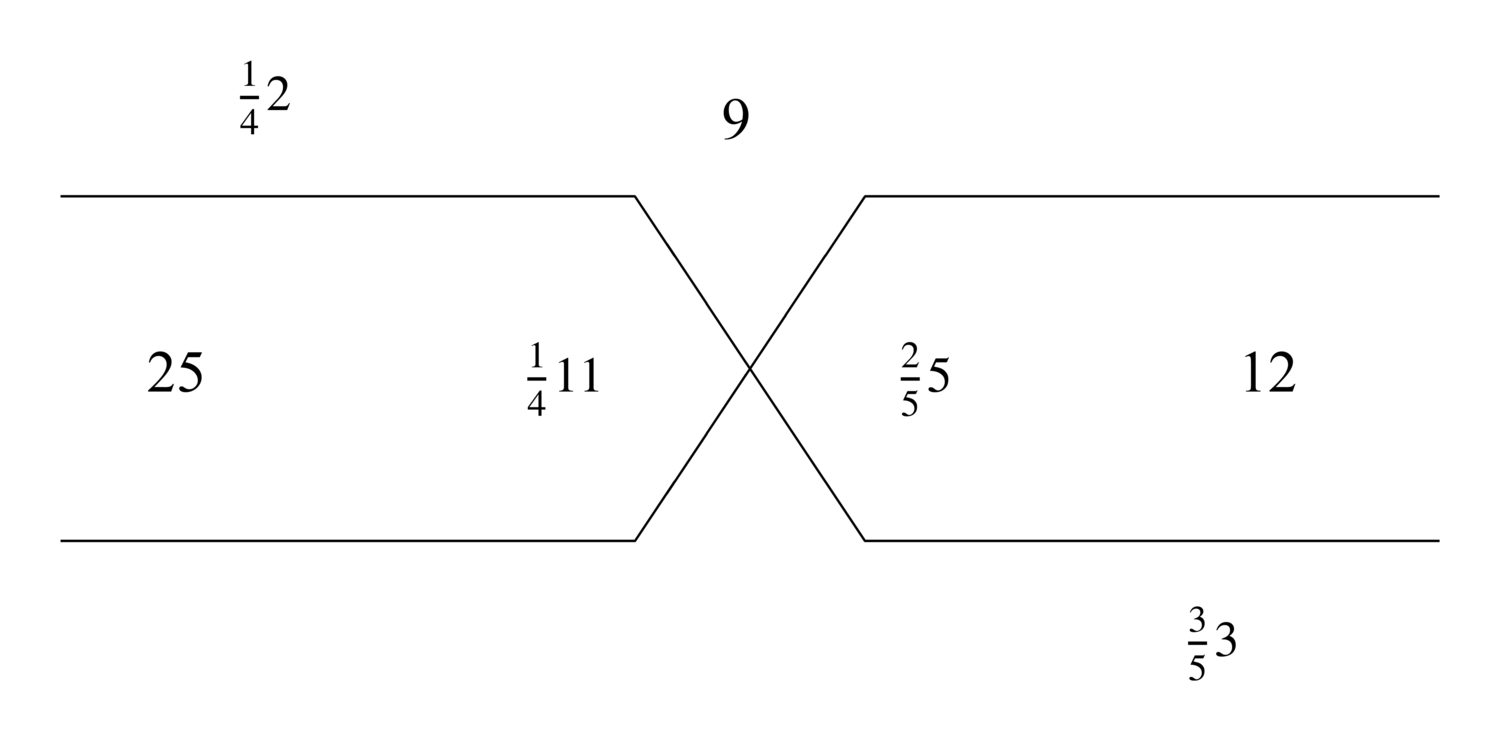
76.7 For addition with a disparity like that of the chessboard squares and similar [problems], a one [is placed] in the first square, then one proceeds by doubling from the first [square] to another assigned [square]. You add one to the one that is in the first square to get what is in the second square. Then you multiply that by itself, so the outcome is what is in the second square and what is before it, with an added one. Then you also multiply that by itself, so the outcome is what is in the fourth square and what is before it, with an added one.23 Continuing, you also multiply the result by itself, and you double the squares,24 until you reach the assigned [square], and you drop the one from the sum. The remainder is the required number.
77.9 If the situation is different, then multiply the remainder by the first square to get the required number.27 A different situation is when the first square is something other than one.
78.1 If the numbers have another disparity, then multiply the smallest by how much the greatest exceeds it, and divide [the result] by the difference between the smallest and the number that follows it. Then add the result to the greatest. This gives the required number.28
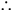 54
54
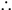 36
36
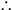 24
24
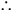 16. We multiply the smallest, which is the sixteen, by how much the eighty-one exceeds it, since it is the greatest of the numbers, and that is sixty-five. The result is one thousand forty, whose figure is 1040. Then we divide it by the difference between the sixteen and the number after it, which is the twenty-four, and that is eight. The result of the division is one hundred thirty, whose figure is 130. We add it to the greatest to get two hundred eleven, whose figure is 211, and it is the required number.
16. We multiply the smallest, which is the sixteen, by how much the eighty-one exceeds it, since it is the greatest of the numbers, and that is sixty-five. The result is one thousand forty, whose figure is 1040. Then we divide it by the difference between the sixteen and the number after it, which is the twenty-four, and that is eight. The result of the division is one hundred thirty, whose figure is 130. We add it to the greatest to get two hundred eleven, whose figure is 211, and it is the required number.
79.1 If the disparity of the numbers is through a known number other than doubling, then multiply the disparity by the number of numbers less one. Adding the first number to the result gives the last of the numbers. Add it to the first, and multiply it by half of the number of numbers. It yields the required answer.30
79.13 For the addition of consecutive numbers, you multiply half of the upper extreme by the upper extreme and one.31 For example, suppose we want to add from one to ten consecutively. We add one to the ten, the upper extreme, and that is eleven. We multiply it by half of the ten, giving fifty-five, which is the sum, and its figure is 55.
80.5 For the addition of consecutive odd numbers you square half of the established upper extreme with the one. For example, suppose we want to add the odd numbers from one to nine consecutively. We add one to the nine, the upper extreme, giving ten. We then multiply half of the ten by itself, giving twenty-five, which is the required number, and its figure is 25.
80.20 For the addition of consecutive even numbers, you always add two to the upper extreme, and you multiply half of the sum by half of the upper extreme. For example, suppose we want to add the even numbers from two to ten consecutively. We add two to the ten, the upper extreme, giving twelve. We multiply its half by half of the ten, giving thirty, which is the sum, and its figure is 30.
83.1 Section Three, on subtraction.
83.2 Subtraction is the search for the remainder after the dropping of one of two numbers from the other. It comes in two types. [One] type is subtracting the smaller from the greater one time. And [another] type is subtracting the smaller from the greater more than one time, until the greater vanishes or it leaves a remainder less than the smaller. This type is called testing by casting out.
![\begin{matrix}5035\\[-.5mm]4968\end{matrix}](../../../media/sources/14/4/EOAineq_4_7.png) .
.
![\begin{matrix}{0067}\\[-.5mm]5035\\[-.5mm]4968\end{matrix}](../../../media/sources/14/4/EOAineq_4_8.png) .
.
84.13 Here is another example of subtraction from the first [rank]. Suppose we want to subtract three thousand four hundred sixty-nine from six thousand five hundred forty-three. We put them down in two parallel lines, as mentioned, as in this figure:
![\begin{matrix}6543\\[-.5mm]3469\end{matrix}](../../../media/sources/14/4/EOAineq_4_9.png) . We subtract the nine that is in the units rank from its counterpart in the minuend, which is three. [This is] smaller than the nine, so we add ten to the three of the minuend, giving thirteen. We subtract the nine from it. The remainder is four. We put it above the three, then we add one to the six that is in the tens rank of the subtrahend, giving seven. We likewise subtract it from its counterpart, which is four. [This is] smaller than the seven, so we add ten to the four, giving fourteen. We subtract the seven from it, leaving seven. We put it above the four. Then we add one to the four that is in the hundreds rank, giving five. We likewise subtract it from its counterpart, which is five, and it vanishes. So we put a zero above the five. Then we likewise subtract the three that is in the thousands rank – with nothing added to it, since nothing remains from the previous position – from its counterpart, which is the six. Three remains, and we put it above the six. This completes the work. The remainder is three thousand seventy-four, and the figure for that is 3074.33
. We subtract the nine that is in the units rank from its counterpart in the minuend, which is three. [This is] smaller than the nine, so we add ten to the three of the minuend, giving thirteen. We subtract the nine from it. The remainder is four. We put it above the three, then we add one to the six that is in the tens rank of the subtrahend, giving seven. We likewise subtract it from its counterpart, which is four. [This is] smaller than the seven, so we add ten to the four, giving fourteen. We subtract the seven from it, leaving seven. We put it above the four. Then we add one to the four that is in the hundreds rank, giving five. We likewise subtract it from its counterpart, which is five, and it vanishes. So we put a zero above the five. Then we likewise subtract the three that is in the thousands rank – with nothing added to it, since nothing remains from the previous position – from its counterpart, which is the six. Three remains, and we put it above the six. This completes the work. The remainder is three thousand seventy-four, and the figure for that is 3074.33
85.16 In the first way of checking34 a subtraction by addition you should look for a number which, if you add it to the subtrahend, then [the sum] is equal to the minuend. One begins this from the first of the ranks, just like those who work with rūmī signs do.
86.1 Whenever you are faced with subtracting a number from a number, and then the remainder from another number, and so on, then you work it out in the steps as indicated in this section.
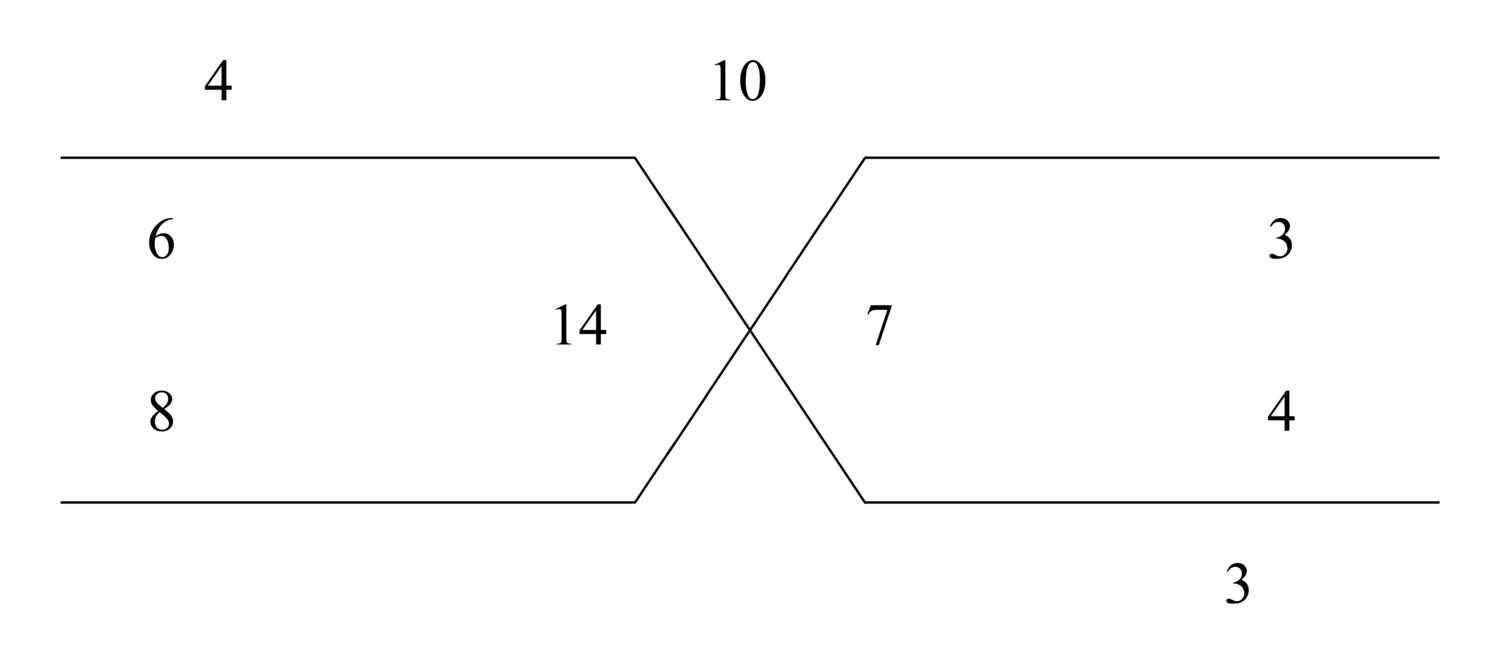
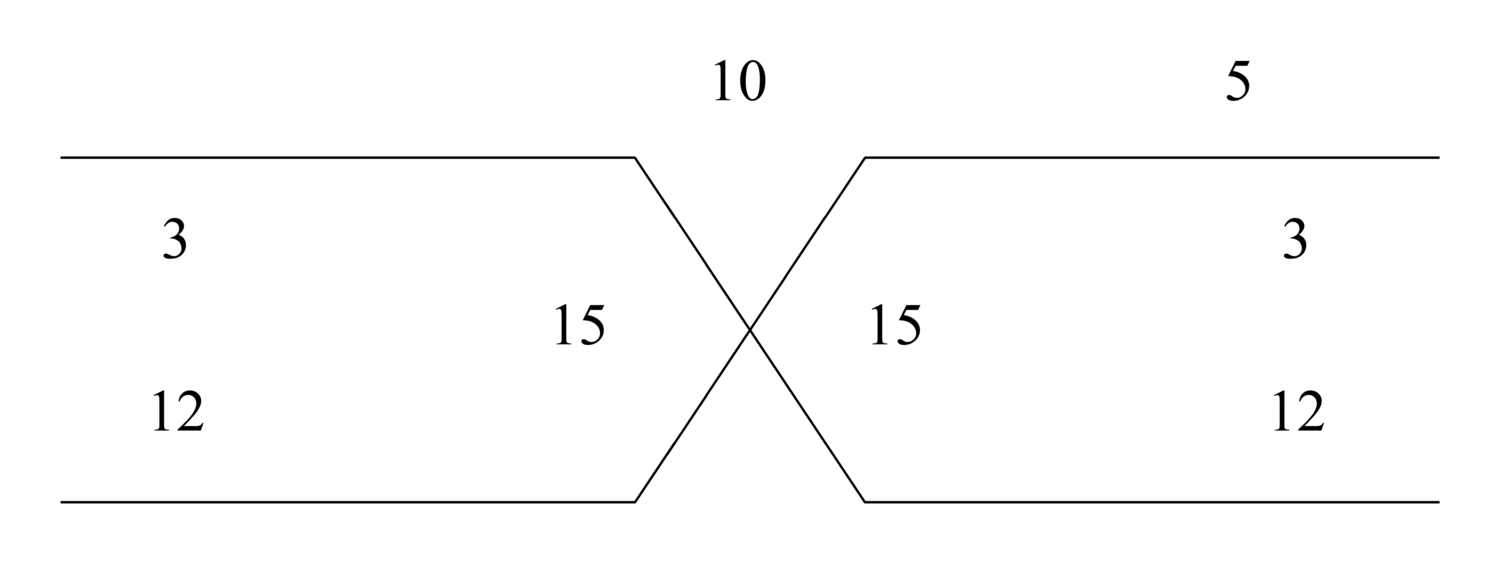
![2~\scalebox {-1}[1]{\ell }~5~\scalebox {-1}[1]{\ell }~7~\scalebox {-1}[1]{\ell }~8~\scalebox {-1}[1]{\ell }~10](../../../media/sources/14/4/EOAineq_4_11.png) . We subtract the two from the five, and the remainder from the seven, and the remainder from the eight, and the remainder from the ten, leaving six, which is the required number.
. We subtract the two from the five, and the remainder from the seven, and the remainder from the eight, and the remainder from the ten, leaving six, which is the required number.
86.15 If we wish, we can add the even subtrahends, which are the seven and the two, with the minuend ten, to get nineteen. Then we add the odd subtrahends, which are the eight and the five, giving thirteen. We subtract it from the nineteen, leaving six.
86.18 And if we wish, we can consider three successive terms. We subtract the middle from the sum of the extremes, leaving the remainder as one number. We insert it in [their] place in the subtrahend. Then we likewise consider it and the two remaining numbers. Take for example the ten and the eight and the seven. We drop the eight from seventeen, the sum of the extremes, leaving nine which, with the two and the five, are three successive numbers. We drop the five from the sum of the extremes, leaving six.
87.9 And if we wish, we can subtract the eight from the ten, and add the remainder to the seven, and subtract the five from it, and add the remainder to the two, yielding six.
87.11 The cause of this is that when subtracting the deleted from the appended, it is deleted, but when subtracting the deleted from another deleted, it is appended. Thus the deleted second and fourth and sixth of the even terms are always appended, since each of them is deleted from a deleted. And the odd terms are always deleted, since they are deleted from an appended.36 So know it.
87.15 The second type [of subtraction] consists of three [kinds of] subtractions. These are frequently used in checking work. One is casting out nines, the second is casting out eights, and the third is casting out sevens.
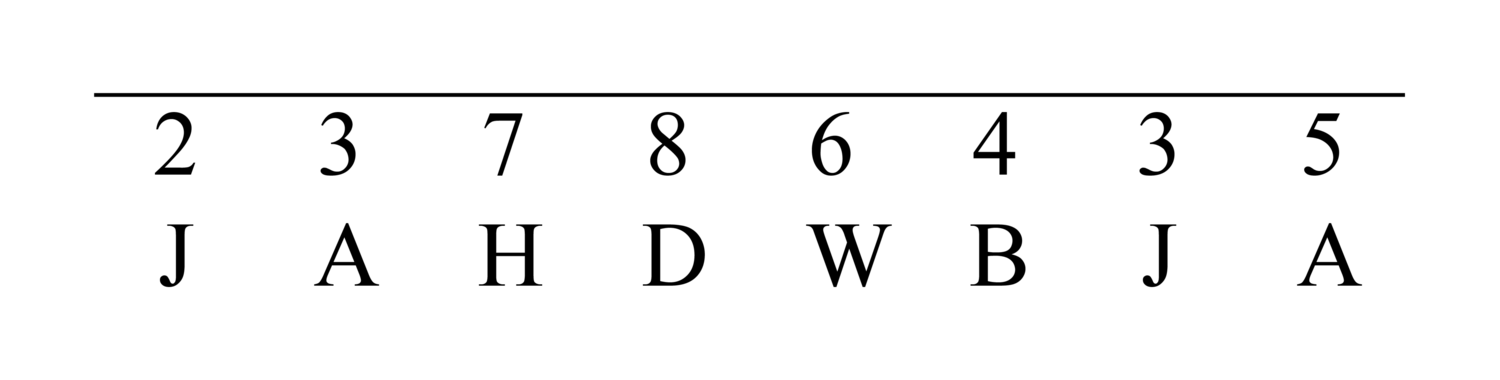
88.10 In casting out sevens, three remains from each ten, two from each hundred, six from each thousand, four from each ten thousand, five from each hundred thousand, one from each million, and from there the cycle begins again. You can come to know it with these letters: A J B W D H, repeated below the digits.
88.17 If you wish, you can write down the letters as mentioned, or if you wish you can make them dust numerals. You multiply each digit by what is below it in number – sound out the letters – and you cast out sevens. You leave its residue above it. Then you add all the digits of the remainders as if they were units and you cast out sevens.
89.4 For example, suppose we want to cast out [sevens from] twenty-three million seven hundred eighty-six thousand four hundred thirty-five. We write it down on a line and we draw a line above it. We write the letters below it, each letter below a number consecutively. If we run out of letters and we have not run out of digits, we repeat the letters for the remaining [digits]. This is what he meant when he said “and from there the cycle begins again”. That is, after the H, and for the rest of the number, the letters are repeated along with the quantity with it. The figure always looks like this:
90.3 If you wish, multiply what is in the last place by three. You cast out sevens, and you add the remainder to what is before it. If there is no number in the place before it, then you multiply the accumulated residue by three and you cast out sevens. Keep doing this until you reach the units [place].
90.15 If you wish, make the last digit tens and add what is before it as if it were units, and then cast out sevens. Then you make the remainder tens and you add it to what is before it as if it were units, and you cast out again.
91.1 Subsection on the way to test [calculations] by casting-out.
91.4 For example, we added forty-three, whose figure is 43, to sixty-four, whose figure is 64. The sum is one hundred seven, whose figure is 107. We can check this problem and other problems by casting out nines or eights or sevens. However, many people cast out sevens. We want to check this problem likewise, as well as the other examples. We add the one, the remainder of the addend, to the one, the remainder of the augend, giving two, which is the answer. If the sum of the two remainders can be cast out, we cast it out also, and its remainder is the answer. Then we cast out the sum, leaving two, which agrees with the answer. So know it.
92.3 And if this residual four of the subtrahend were greater than the residual five of the minuend, then we add [the modulus] to the five, the number of the minuend: nine if it is nine, eight if it is eight, or seven if it is seven. Then we cast out the remainder [in the problem], leaving one, which agrees with the answer. And if we add the four, the residue of the subtrahend, to the one, the residue of the remainder, it is the same as the five, the residue of the minuend. So know it.
92.17 For example, suppose someone said, “Multiply a third by fourteen and a fourth”. The result of the multiplication is four and three fourths, according to what will come in the work on fractions,38 almighty God willing. If we want to check it [by casting out sevens], we multiply the third, which is the remainder of one of the two multiplicands, by the fourth, the remainder of the other multiplicand, resulting in a third of a fourth. Its remainder after its numeration is one, which is a third of a fourth, which is the answer. Then we numerate the result of the multiplication, which gives nineteen fourths. Its remainder is five fourths. We numerate it by a third by multiplying it by three, giving fifteen. Its remainder is one, which is a third of a fourth, equal to the answer in quantity and quality.39
93.6 For division and denomination, you cast out the result and the divisor or denominating number. You multiply the remainder of one of them by the remainder of the other, and keep it in mind. The remainder is the answer. Then you cast out the dividend or denominated number, which should agree with the answer. This method also generalizes to whole numbers and to fractions, after numerating them.
93.10 Here is an example of division. We divide one thousand four hundred eighty-eight, whose figure is 1488, by twelve. The result of the division is one hundred twenty-four, whose figure is 124. If we want to check it, we multiply the residual five of the result by the residual five of the divisor, giving twenty-five. Its remainder is four, which is the answer. Then we cast out the dividend, whose remainder is four, which agrees with the answer.
93.15 Here is an example with fractions. Suppose someone said to you, “Divide five sixths and three fourths by a half”. The result of the division is three and a sixth, and its remainder, after numerating it, is five sixths. We multiply it by one, the numerator of the half, which is the divisor, giving five halves of a sixth. We then multiply it by two so it becomes fourths of sixths, agreeing in the numeration with the numerated dividend. It gives ten. Its remainder is three fourths of a sixth, which is the answer. Then we cast out the numerated dividend, which is thirty-eight fourths of a sixth. Its remainder is three fourths of a sixth, which is equal to the answer.40
94.1 Here is an example of denomination. Suppose someone said, “Denominate eleven with fifteen”. The result of the denomination is three fifths and two thirds of a fifth. The remainder after numerating it is four. We multiply it by the one, the remainder of the denominating number, giving four, which is the answer. Then we cast out the denominated number. Its remainder is four, equal to the answer.
94.5 Here is an example with fractions. Suppose someone said, “Denominate two sixths and two thirds of a sixth with five eighths and a third of an eighth”. It results in two-thirds, and the remainder of its numerator is two. We multiply it by the two, the remainder from numerating the denominating number, giving four thirds of a third of an eighth. Then [we multiply it] by the six, giving twenty-four thirds of a third of a sixth of an eighth. Its remainder is three, which is the answer. Then we cast out the numeration of the numerator. Its remainder is one. We multiply it by the three, then by the eight. It gives twenty-four thirds of a third of a sixth of an eighth. Its remainder is three, which equals the answer.
95.1 Section Four, on multiplication and understanding its subtleties.
95.2 Multiplication consists of the duplication of one of two numbers by however many units are in the other.
95.3 This section covers two types. [In one] type, in putting down the multiplier, each one of them is equal to the one of the multiplicand. Here the duplication clearly occurs in both the term and the meaning.
95.15 [Multiplication] is divided into three kinds; that is, with regard to procedure. The first kind is by shifting, the second by half-shifting, and the third without any shifting.
95.17 The first kind, which is multiplication by shifting, calls for erasing, and is called sleeper [multiplication]. You write the multiplicand and the multiplier on two lines so that the first digit of the multiplier is below the last digit of the multiplicand. Then you multiply it by all the digits of the multiplier. You begin by writing the result in its place, traversing the line, continuing along the line of the multiplicand. Then you shift the number of the multiplier so that it is below the digit that follows those before it. Then you multiply it by all the digits of the lower number, like the first time. Whenever you multiply by a number, you add the result with what is over the head of that number from the previous result, and you put it where it belongs. This procedure is universal for all problems of multiplication.
96.3 For example, if we want to multiply forty-three by fifty-four, we write down the forty-three, the multiplicand, on a line, and the fifty-four, the multiplier, on another line, so that the first digit of the multiplier is below the last digit of the multiplicand, as mentioned. Here is the figure:
We multiply the last digit43 of the multiplicand, which is the four, by the five, the last digit of the multiplier, giving twenty. We put a zero above the five, and the twenty, in the form of a two, after the zero. We also multiply it by the four below it, giving sixteen. We put the six in its place, and the ten, in the form of a one, in place of the zero. These are included with the line of the multiplicand. Then we shift the multiplier back one place, so the four is below the three, and the five is below the six. This is the figure:
97.1 The other type is known as vertical [multiplication]. You set up the two multiplicands in two vertical lines so that the first digit of the multiplier is opposite the last digit of the multiplicand. You proceed in multiplying them just as you did in the sleeper method, by shifting and erasing.
98.4 The second kind is multiplication by half-shifting, which only works for two equal numbers. In this scheme you write down one of the equal numbers on a line, and you put marks in the form of dots between its digits. Then you multiply the last digit by itself and you put the result above it. Then you double it and you shift it by writing it down in place of the dot preceding it. Then you multiply the preceding digit by the shifted number and by itself, and you write the results of each multiplication above them. Then you double the digit that you just multiplied, as you did before. Then you shift it in place of the dot that precedes it. Then you shift the first doubled number, [adding] to its calculation. Then you multiply the digit preceding the dot that was replaced by all the doubled number, then by itself, as you did before. You continue in the same way, doubling, shifting, and multiplying until you reach the end of the line.45
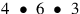 . We multiply the last four by itself, giving sixteen. We put the six above the four, and the ten, in the form of a one, after the six. Then we double it, giving eight, and we put it in place of the dot preceding it. So it yields this figure:
. We multiply the last four by itself, giving sixteen. We put the six above the four, and the ten, in the form of a one, after the six. Then we double it, giving eight, and we put it in place of the dot preceding it. So it yields this figure:
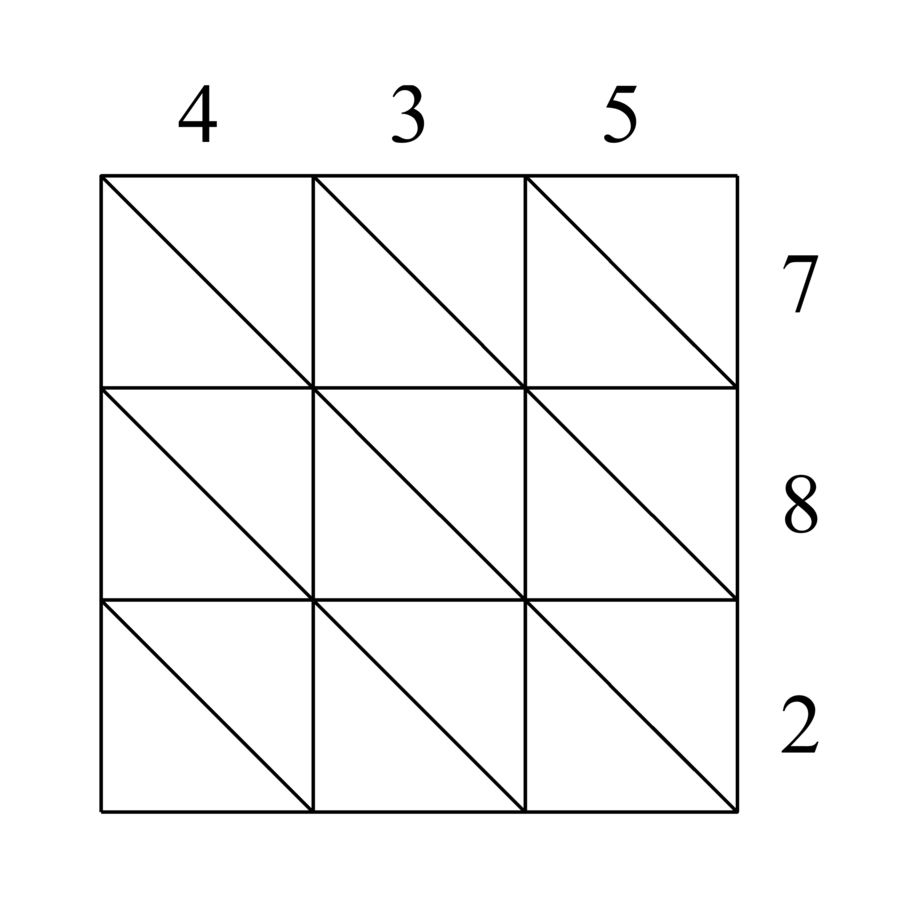
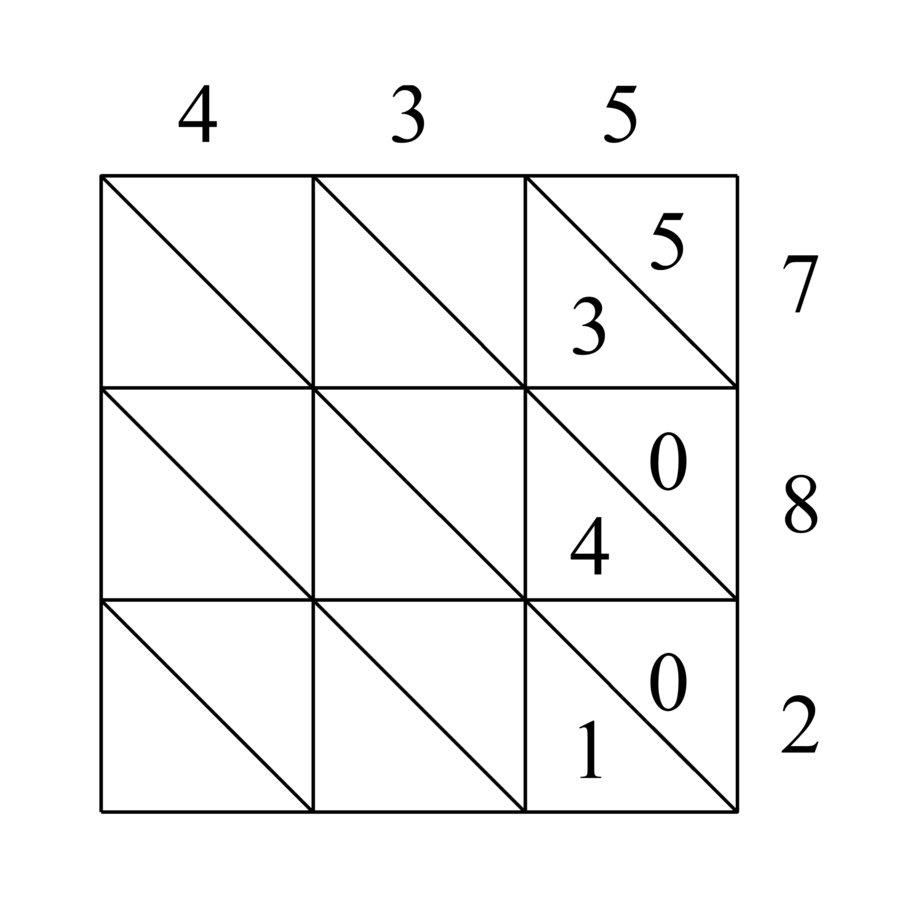
99.14 The third kind is multiplication without shifting, of which there are several types. One is table multiplication, in which you draw a quadrilateral surface, extending length and width according to the ranks in the two numbers to be multiplied. You draw diagonals through its squares from the lower right to the upper left, and you write the multiplicand above the quadrilateral, matching each digit with a column. Then you write the multiplier down the left or right side of the quadrilateral, so that each digit also corresponds to a row. Then you multiply digit after digit of the multiplicand by all the digits of the multiplier, and you put the digits of each rank in the intersecting square. And the meaning of “intersection” is where they meet. You put the units above the diagonal and the tens below it. Then you begin adding from the upper right corner. You add what is between the diagonals, without erasing, and you write each number in its rank, and you add the tens of each sum to the next diagonal. You then put it together, and the sum that you obtain is the result.
101.16 Another [type] is vertical multiplication, in which you draw two vertical lines with some empty space between them, and you draw the two multiplicands beside them. Then you multiply one of them, digit by digit, by all the digits of the other, and you put the results in the space between the lines, taking into account the ranks of the indexes.
103.14 [Another type] is sleeper multiplication. You put the two multiplicands in two parallel lines. Then you multiply each digit of one of them by each digit of the other, and you put down the result taking into account the ranks of the indexes. You may start the multiplication from the first digit or the last. This type is also called multiplication by indexes.
104.1 I say that we need here an introductory remark for this type that may also be useful for rūmī multiplication. The result of multiplying the units is units, since it comes from multiplying a number by a number. The index of the result is the sum of the indexes of the two multiplied numbers less one, as shown by the author, God be satisfied by him, in the section on addition in Lifting the Veil.46 Certainly the index of the multiplicand is one and the index of the multiplier is one, so their sum is two. Dropping one leaves one, and the name of the one, according to what [was said] before, is units.47 So the result of multiplying the units by the units is units. Likewise, their product by the tens is also tens, and by the hundreds is hundreds. And multiplying the tens by the tens is hundreds, and by the hundreds is thousands. And the hundreds by the hundreds is tens of thousands. This is the end of the introductory remark.
106.11 Another type [of multiplication] requires that the [numbers of] digits of the multiplicands be equal, and that the digits in each rank of the ranks in each line also be equal. The way to write it down is similar to the way [for the method] by erasing. Then you write a one below the first rank of the ranks of the upper line, and a two below the second [rank], likewise increasing by one until you reach the last rank of the multiplicand. What is below it is shared with the first rank of the multiplier. From the second rank of the multiplier you begin decreasing one by one until you reach the last rank of the multiplier. These written numbers are all on a third line. The indexes of the ranks of the multiplicand are in the correct order, but the indexes of the ranks of the multiplier are reversed. Then you multiply the number of the rank of the multiplicand by the number of the rank of the multiplier. The result is multiplied by what is in the written line, and the result is the required number. This type of multiplication is called “by repetition”.
Then we write a one below the first four, a two below the second, and a three below the third. This is the first rank of the multiplier. Then we write a two below the second three, since from this point we begin decreasing one by one, as mentioned, and a one below the third three, as in this figure:
As mentioned, the indexes of the ranks of the multiplicand are in the correct order, and the indexes of the ranks of the multiplier are reversed, since the index of the three in the first [rank] of the multiplier is one, and we wrote it below the third three, which is its last rank.
108.9 Another [type] is multiplication by excess, in which you denominate the excess over ten of one of the two multiplicands with the ten. Then you take that ratio of the other [multiplicand]. You add it to it and you make it tens. If the ratio has a fractional part, you take it with respect to the ten49 and you put it in the units place.
109.7 Another type is known as denomination. Here you add the two multiplicands, then you denominate one of them with the sum. Then you take that ratio of the other [multiplicand] and you multiply it by the sum, so the result is the required number.50
109.16 And recall what the jurist Abū Muḥammad ibn Ḥajjāj, known as Ibn al-Yāsamīn,
109.19 Another type is also known as denomination. You denominate the most convenient of the two multiplicands with whatever simple power of ten you wish, or you divide it by it. Then you multiply the result of the denomination or division by the other [multiplicand]. Then you raise each [digit] of the result by the power of ten of the divisor. The outcome is the required number.
110.5 And by “simple power of ten” we mean that the first [non-zero] rank is equal to the ten or the hundred or the like.
110.12 And another example: suppose we want to multiply twelve by fifteen. We divide the fifteen by the ten, resulting in one and a half. We multiply it by the twelve. The result of the multiplication is eighteen. We raise each [digit] by the ten, the divided power of ten, yielding one hundred eighty, which is the required number.
111.1 Another example: we want to multiply three by fifteen. So we add two to the three, giving five. We denominate it with the ten, giving a half. We multiply it by the fifteen. The result of the multiplication is seven and a half. We raise each [digit] by ten, the power of ten, and half of the ten, to get seventy-five. We drop from it the product of the added two by the fifteen, since it was not added to it. The remainder is the required number, and that is forty-five, and its figure is 45.
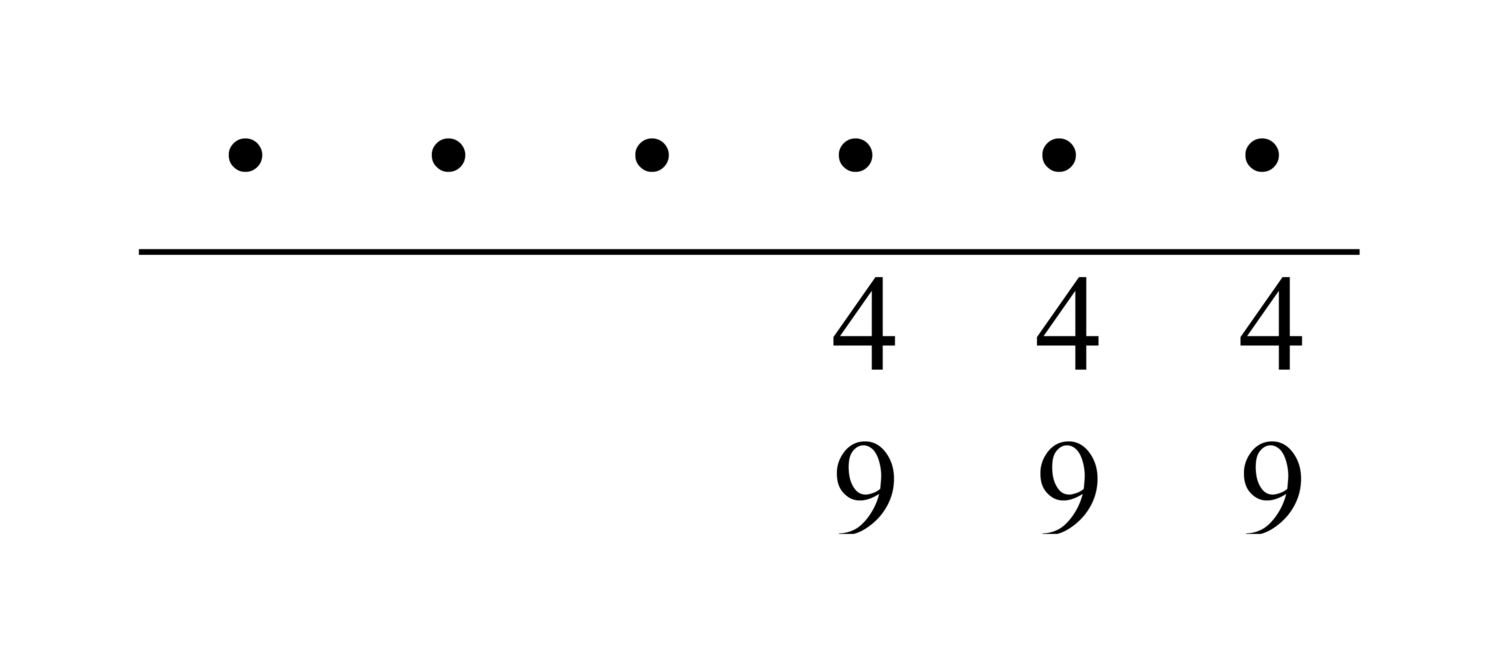
111.7 [Another type] is multiplication of “nines”, with the requirements that the [numbers of] ranks in the two lines be equal, one of them consist of all nines, and the digits of the other be equal. A description of the procedure is that you write down the two parallel lines, one of them below the other, and you put dots above them, as many as there are places in them. You multiply the digit of the place of one of them by the digit of the place of the other. You put the units of the result in the first of the dots, and its tens in the middle of the remaining dots. You note the difference between the nine and the digit of the multiplier. Then with [this difference] you fill in what is between the two digits of the results, I mean the units and the tens, and you fill the remaining dots with the digit that is different from the nine. What this yields is the answer.52
112.5 Another type of multiplication of nines has no condition. Instead, the digits in one of the lines are nines, and the digits in the other line can be whatever they are, and the number of places can also be whatever they are. To work it out, you add as many zeros to the ranks of the other line as the number of ranks of the nines. Then you subtract from the total the number different from the nines, leaving the answer.53
112.16 Another type is known as squaring. You take half of the sum of the multiplicands and you square it. You subtract from the result a square of half of the difference between them. The remainder is the result of the multiplication.54
113.6 Another type is also known as squaring, which is that you multiply a square of one of the two multiplicands by what results from the ratio of the other to the number you squared, or you divide a square of one of them by the result of dividing the squared one by the other one.
113.16 Another type is that you multiply the difference between the two multiplicands by the greater of them, and you drop the result from a square of the greater. Or you multiply the difference by the smaller of them and you add the result to a square of the smaller. The result is the required number.55
114.4 And if you multiply a number with zeros by a number with zeros, multiply the parts of one by the parts of the other, stripped of the zeros. Then you dress the result with all the zeros. The outcome is the required number,56 since multiplying the number by the zero or the zero by the number is identical. It comes from voiding the number or duplicating zero. Neither of these gives a number, so its sign is always a zero.
115.1 The student should memorize the following breakdown and master it, which is:
117.1 Section Five, on division.
117.2 Division is the decomposition of the dividend into equal parts in such a way that its number is equal to what is in the divisor in units.57 This applies to discrete quantities.58
117.9 Division has two meanings. One of them is described first, which concerns the division of a type by another type, like dirhams by men. The other is described second, and concerns the division of a type by the same type. So the word “division” has two meanings. And it should not be given a single description without regard to circumstances, as most people do. The meaning many people give it is specifically the first meaning, and they ignore the second meaning. Their description without regard to circumstances misleads the general public to lump the two meanings together, or to think that division truly has one meaning, and this is not so.61
117.16 Here is an example of division with the first meaning. Divide fifteen dirhams among three men. We decompose the fifteen into three equal parts, which is how many units are in the divisor. So each part consists of five dirhams, which is how many whole units there are of that three, the divisor.
118.14 Division comes in two types: dividing a greater number by a smaller number and dividing a smaller number by a greater number. Dividing the smaller by the greater specifically is called “denomination”, and the word “division” is reserved for dividing the greater by the smaller.
118.17 The usual way of dividing the greater by the smaller is that you write the dividend on a line, and you write the divisor below it, making sure that the greater is not below the smaller. Then look for a number to put below the first digit of the digits of the divisor so that when you multiply it by all of its digits, it either exhausts the entire dividend or it leaves a remainder smaller than the divisor, in which case you denominate it with it.
So, it happens that the divisor is below the twenty-four. If it were smaller, say for example eleven or ten or something similar, we would still put down the last digit of the divisor below the last digit of the dividend.
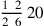 . Similar problems are worked out the same way.
. Similar problems are worked out the same way.
119.18 If you want, you can divide the dividend into parts and add the quotients to get the result. Or you can decompose the divisor into the numbers of which it is composed and make them denominators, and divide the dividend by them. Or you can reconcile the dividend and the divisor and divide the reconciled divisor by the reconciled dividend.
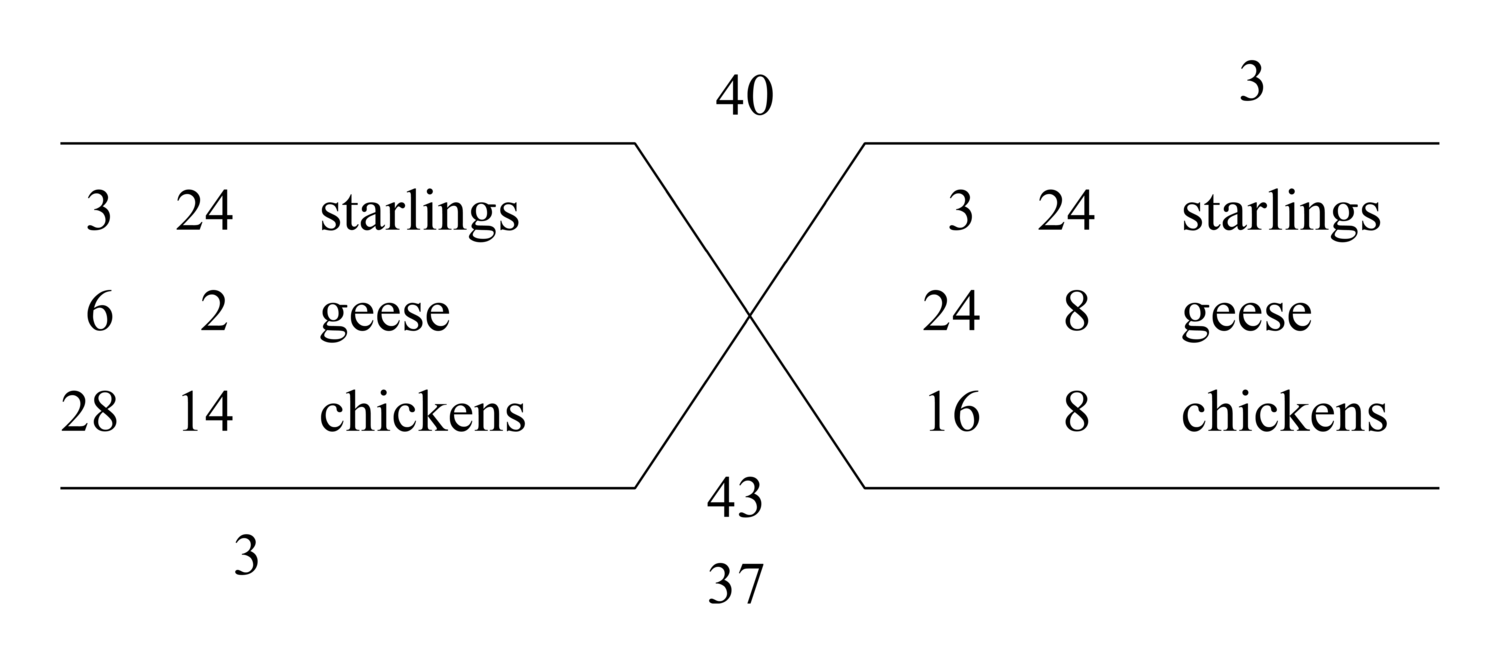
120.20 [Another] type of division is specifically called apportionment. The way you work it out is that you add the apportioned parts and you take it to be a denominator. Then you multiply each of the apportioned parts by the dividend, and you divide the results by the denominator, giving the required number.
121.14 There are four other ways to do this. One of them is that we denominate what each of them has in hand with the denominator, and we multiply the result by the dividend. This gives the required number. The second is that we denominate the dividend with the denominator, and what results is called the part of the share. We multiply it by what each one has in hand, giving the required number. In the third, we divide the denominator by what each one has in hand, and we divide the dividend by the results, giving the required number. In the fourth we divide the denominator by the dividend and we divide what each one has in hand by the results. This gives the required number.
122.2 In the case that the apportioned parts are fractions, multiply everything in the problem by the smallest number divisible by the denominators. And if all of the parts have a common divisor, remove it by exchanging the parts or reconciling them.
123.18 For denomination, the most well-known way is that you decompose the denominating number into the numbers of which it is composed, and you take them as denominators. Then you divide what you want to denominate by them, resulting in the answer. One obtains its value by means of the ratio of these parts to the denominators serving as divisors.
123.22 For example, suppose someone said, “Denominate eleven with fifteen”. We decompose the fifteen, the denominating number, into the numbers from which it is composed, which are five and three. We put them below a line and we divide the eleven first by the three, and we put the remainder above it. And we divide the quotient by the five, which is smaller than it. We put it above it, so it yields this figure:
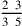 . Thus we form the ratio of the three to the five that is below it, and the two to the three that is below it, and we attach the ratio to the five. This gives the size of eleven with respect to fifteen, which is three fifths and two thirds of a fifth. So know it.
. Thus we form the ratio of the three to the five that is below it, and the two to the three that is below it, and we attach the ratio to the five. This gives the size of eleven with respect to fifteen, which is three fifths and two thirds of a fifth. So know it.
124.8 A lesser known way is that you divide the denominating number by the denominated number, and you denominate one with the result. Or you denominate one with the denominating number and you take this ratio of the denominated number. Or you multiply the denominated number by some [convenient] number and you divide the result by the denominating number, and [you divide] the result by that multiplied number.66
124.20 To decompose numbers requires that some preliminary remarks be learned. They are:
125.5 If it begins with a five, it has a fifth. If it begins with units, and if it is even, then one casts out numbers using one of the three moduli, in the sense of what is said above on casting out. If it is cast out entirely by nines, then it has a ninth and a sixth and a third. For example, thirty-six is cast out entirely by nines. Its ninth is four, its sixth is six, and its third is twelve.
126.14 If it is not cast out entirely, then look for deaf parts by dividing by them; and you continue dividing the required number to be decomposed by deaf parts until you arrive at a number that divides into it, or you get a number whose square is greater than your given number, or [equivalently, that] the result from the division is equal to or less than the divisor and leaves a remainder after the division. At this point you know that it is one of the deaf parts, and the denomination is formed from it.
127.9 Subsection on finding deaf parts.
128.1 If we want to know which among them is composite with three, we count it off from its cell, ending at the cell of the seven, so the nine that is next is composite with the three. So we put a mark above it. Similarly, we count beginning with the cell of the nine, ending with the cell of the thirteen. So the fifteen that is next is also composite with the three, and we put a mark above it. Do this until the end of the sieve. Likewise, do this with the five and the seven, but not with the nine, since it is composite, and not with any other composite number. This ends in our example with counting by thirteen. We know that the work is finished because its square is one hundred sixty-nine, which is greater than one hundred forty-five, which is the last number in the prescribed sieve.
129.1 Section Six, on restoration and reduction.
131.1 Chapter Two, on fractions.
133.3 For example, three and six. The relation that arises with the ratio of the smaller to the greater is called the fraction. It cannot be named in terms of the three alone because of the separation, and likewise it cannot be named in terms of the six alone; nor in terms of [the two words] taken together, since the ratio is not a sensible object but is the idea of a specific intelligible object. It is called a fraction, like terrain with fractures that ascends and descends; or also like the surface, the solid, and the line, and there is nothing of this in discrete quantities except similar abstractions. Furthermore, the fraction consists of names, like “the half” and others that will be presented below, almighty God willing.
134.1 Section One, on the names of fractions and numerating them.
134.2 Ten fractions have simple names. The first is the half, which is the greatest, whose figure is
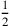 . Then the third, whose figure is
. Then the third, whose figure is
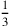 . Then the fourth, whose figure is
. Then the fourth, whose figure is
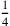 . Then the fifth, whose figure is
. Then the fifth, whose figure is
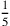 . Then the sixth, whose figure is
. Then the sixth, whose figure is
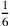 . Then the seventh, whose figure is
. Then the seventh, whose figure is
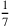 . Then the eighth, whose figure is
. Then the eighth, whose figure is
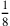 . Then the ninth, whose figure is
. Then the ninth, whose figure is
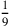 . Then the tenth, whose figure is
. Then the tenth, whose figure is
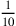 . Then the “part”, of which there are many types. You can say a part of eleven, whose figure is
. Then the “part”, of which there are many types. You can say a part of eleven, whose figure is
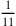 , and a part of seventeen, whose figure is
, and a part of seventeen, whose figure is
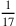 , and so on.
, and so on.
135.1 You can attach these simple names to one another so that the resulting name is a combination of two or more names. For example, we say two eighths and a seventh of an eighth, whose figure is
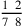 , and likewise for similar examples. Another example is eight ninths and four sevenths of a ninth and two sixths of a seventh of a ninth and a third of a sixth of a seventh of a ninth, whose figure is
, and likewise for similar examples. Another example is eight ninths and four sevenths of a ninth and two sixths of a seventh of a ninth and a third of a sixth of a seventh of a ninth, whose figure is
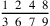 , and likewise for similar examples.
, and likewise for similar examples.
135.8 Numeration is that you reduce all of what is given to you in a particular problem to a finer fraction in it…69 Know that the finer fraction in it is the part named with respect to all the denominators of the problem.
135.10 When the fraction is related, like five-sixths and four-fifths of a sixth and two-thirds of a fifth of a sixth, whose figure is
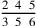 , we multiply what is above the first denominator by the denominator that follows it. That means to relinquish its name, which is sixths, in favor of fifths of sixths, since the second denominator is a number of what is in the one of the first denominator in units. So we add it with the four that is above it, since they are fifths of sixths, then we multiply that by the three, the third denominator, which is the number of what is in the one of the second denominator in units. This results in thirds of fifths of sixths. We add it with the two, since it is thirds of a fifth of a sixth. This gives the numerator of the problem, which is how many thirds of fifths of sixths there are in it, and that is eighty-nine. The multiplication of the denominators one by the other, which is ninety, is what is in the whole one of these parts, and a part of one of them is a finer fraction in the problem.
, we multiply what is above the first denominator by the denominator that follows it. That means to relinquish its name, which is sixths, in favor of fifths of sixths, since the second denominator is a number of what is in the one of the first denominator in units. So we add it with the four that is above it, since they are fifths of sixths, then we multiply that by the three, the third denominator, which is the number of what is in the one of the second denominator in units. This results in thirds of fifths of sixths. We add it with the two, since it is thirds of a fifth of a sixth. This gives the numerator of the problem, which is how many thirds of fifths of sixths there are in it, and that is eighty-nine. The multiplication of the denominators one by the other, which is ninety, is what is in the whole one of these parts, and a part of one of them is a finer fraction in the problem.
136.8 If the fraction is distinct, like five-sixths and four-fifths, whose figure is
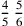 , we multiply the five-sixths by five, the denominator of the fifths, and that is the number of what is in the one sixth of fifths, so it becomes fifths of sixths. And we multiply the four-fifths by six, the denominator of the sixths, and that is the number of what is in the one fifth of sixths. So it becomes fifths of sixths. The sum of these two numerators are parts of thirty, which is sixths of fifths or fifths of sixths, both being equal.
, we multiply the five-sixths by five, the denominator of the fifths, and that is the number of what is in the one sixth of fifths, so it becomes fifths of sixths. And we multiply the four-fifths by six, the denominator of the sixths, and that is the number of what is in the one fifth of sixths. So it becomes fifths of sixths. The sum of these two numerators are parts of thirty, which is sixths of fifths or fifths of sixths, both being equal.
137.1 The fraction may be portioned, in which the fractions are taken one of another, and which is how they are described in the expression. An example is three fourths of five sixths, whose figure is
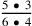 . We multiply the three by the five, giving fifteen fourths of a sixth, or sixths of a fourth, which are parts of twenty-four parts of the unit. This is because five of the sixths, of which we want three of its fourths, [is found] by taking its fourth, which is five fourths of a sixth, and multiplying it by three, giving fifteen fourths of a sixth, or by taking a fourth of three times it. And three times it is its multiplication by three, giving fifteen sixths, and a fourth of that is fifteen fourths of a sixth, which is also fifteen sixths of a fourth. So three fourths of five sixths is five sixths of three fourths, since multiplying three by five is like multiplying five by three.70 So know it.
. We multiply the three by the five, giving fifteen fourths of a sixth, or sixths of a fourth, which are parts of twenty-four parts of the unit. This is because five of the sixths, of which we want three of its fourths, [is found] by taking its fourth, which is five fourths of a sixth, and multiplying it by three, giving fifteen fourths of a sixth, or by taking a fourth of three times it. And three times it is its multiplication by three, giving fifteen sixths, and a fourth of that is fifteen fourths of a sixth, which is also fifteen sixths of a fourth. So three fourths of five sixths is five sixths of three fourths, since multiplying three by five is like multiplying five by three.70 So know it.
137.11 …and this is different for different [kinds] of fractions, that is, the numeration. There are five kinds [of fractions]: simple, related, distinct, portioned, and excluded.
137.13 The numerator of a simple fraction is what is above it. For example, we said “a seventh”: its numerator is the one that is above the line. Likewise for combined fractions, like if we said, “a third of a seventh”: its numerator is also the one that is above the line.
138.1 The numerator of a related fraction is what is above the first denominator multiplied by the next denominator, then adding to the end of the line; or, it is what is above the first denominator multiplied by the denominators after its denominator, and what is above the second denominator also multiplied by the denominators after its denominator, and so forth until the line is completed, then adding them together.
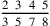 . We multiply the five that is above the first denominator by the seven, the second denominator, and we add the four that is above it, giving thirty-nine. We also multiply that by the five, the third denominator, and we add the three that is above it, giving one hundred ninety-eight. We likewise multiply it by the three, the fourth denominator, and we add the two that is above it to it, giving five hundred ninety-six, which are eighths of sevenths of fifths of thirds. This is the numerator, and its figure is 596.
. We multiply the five that is above the first denominator by the seven, the second denominator, and we add the four that is above it, giving thirty-nine. We also multiply that by the five, the third denominator, and we add the three that is above it, giving one hundred ninety-eight. We likewise multiply it by the three, the fourth denominator, and we add the two that is above it to it, giving five hundred ninety-six, which are eighths of sevenths of fifths of thirds. This is the numerator, and its figure is 596.
139.1 The numerator of a distinct fraction is found by multiplying the numerator of each part by the other denominators, then adding them together.
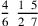 . We find that the first part is related, so we take its numerator in the manner shown above, to get eleven. We multiply it by the six, the denominator of the second part, resulting in sixty-six. Keep it in mind. We find that the second part is simple, so its numerator is the four that is above the denominator. We likewise multiply it by the denominators of the first part, giving fifty-six. We add this with the remembered number to get a total of one hundred twenty-two, which is sevenths of halves of sixths. This is the numerator, and its figure is 122.
. We find that the first part is related, so we take its numerator in the manner shown above, to get eleven. We multiply it by the six, the denominator of the second part, resulting in sixty-six. Keep it in mind. We find that the second part is simple, so its numerator is the four that is above the denominator. We likewise multiply it by the denominators of the first part, giving fifty-six. We add this with the remembered number to get a total of one hundred twenty-two, which is sevenths of halves of sixths. This is the numerator, and its figure is 122.
139.10 The numerator of a portioned fraction is found by multiplying what is above the line, each one by the next.
 .We multiply the seven that is above the first denominator by the five that is above the second denominator, and their product by the three that is above the third denominator, to get the numerator. That comes to one hundred five sevenths of sixths of tenths, and its figure is 105.
.We multiply the seven that is above the first denominator by the five that is above the second denominator, and their product by the three that is above the third denominator, to get the numerator. That comes to one hundred five sevenths of sixths of tenths, and its figure is 105.
140.1 The numerator of an excluded fraction of disconnected [type] is found the same way as for distinct fractions, by subtracting the smaller from the greater.
![{1\over 9}~\scalebox {-1}[1]{\ell }~{6\over 8}](../../../media/sources/14/4/EOAineq_4_34.png) . We multiply the six, the numerator of what is before the “less”, by the nine, the denominator after it, giving fifty-four. From that we drop the product of the one, the numerator after the “less”, by the eight, the denominator before it, which is eight. The remainder is forty-six eighths of ninths, which is the numerator. Work out similar problems the same way, as explained above.
. We multiply the six, the numerator of what is before the “less”, by the nine, the denominator after it, giving fifty-four. From that we drop the product of the one, the numerator after the “less”, by the eight, the denominator before it, which is eight. The remainder is forty-six eighths of ninths, which is the numerator. Work out similar problems the same way, as explained above.
140.14 For the connected [type], multiply the numerator of the diminished fraction by the numerator of the excluded fraction, and likewise multiply by their denominators, and then subtract the smaller from the greater.
![{1\over 3}~\scalebox {-1}[1]{\ell }~{1~\,6\over 2~\,7}](../../../media/sources/14/4/EOAineq_4_35.png) . We take the numerator of what is before the “less”, which is the diminished fraction. We multiply it by the denominators of what is after the “less”, which is the excluded fraction, to get thirty-nine. Keep it in mind. Then we also multiply the numerator of the diminished fraction by the numerator of the excluded fraction, similarly giving the complement thirteen. We drop it from the remembered number. The remainder is twenty-six sevenths of halves of thirds, and it is the numerator.
. We take the numerator of what is before the “less”, which is the diminished fraction. We multiply it by the denominators of what is after the “less”, which is the excluded fraction, to get thirty-nine. Keep it in mind. Then we also multiply the numerator of the diminished fraction by the numerator of the excluded fraction, similarly giving the complement thirteen. We drop it from the remembered number. The remainder is twenty-six sevenths of halves of thirds, and it is the numerator.
141.7 Supplementary remark. If there are repeated deletions in which each of them has the conjunction “and”, it is with respect to the first [term]. And in relation to the first [term], whether they are all connected to or detached from the diminished fraction, [treat them as] distinct fractions excluded from the diminished fraction.71
![{1\over 5}~\scalebox {-1}[1]{\ell }~{1\over 7}~\scalebox {-1}[1]{\ell }~{1\over 4}~\scalebox {-1}[1]{\ell }~{1\over 3}\,5](../../../media/sources/14/4/EOAineq_4_36.png) . The fourth and the seventh and the fifth are distinct fractions excluded from the five and a third, which is the diminished part, and they are all connected to it. Removing the second and third particles of exclusion, the figure in this problem becomes
. The fourth and the seventh and the fifth are distinct fractions excluded from the five and a third, which is the diminished part, and they are all connected to it. Removing the second and third particles of exclusion, the figure in this problem becomes
![{1\over 5}\,{1\over 7}\,{1\over 4}\,\scalebox {-1}[1]{\ell }\,{1\over 3}\,5](../../../media/sources/14/4/EOAineq_4_37.png) . We work it out as before, with the result that the numerator is nine hundred twelve thirds of fourths of sevenths of fifths, and its figure is 912.
. We work it out as before, with the result that the numerator is nine hundred twelve thirds of fourths of sevenths of fifths, and its figure is 912.
142.6 A second example: suppose someone said in the previous problem, “less a fourth of one and less a seventh of one and less a fifth of one”. Then these are distinct fractions removed from the diminished part, which are all detached. Write them also as if they were connected and work it out as before. The result is that the numerator is one thousand nine hundred ninety-one thirds of fourths of sevenths of fifths, and its figure is 1991.
142.10 If the exclusions are repeated without a coordinating conjunction,72 in such a way that each [term] is excluded from the one before it, whether they are detached or connected, then we take the [last] excluded fraction and the diminished fraction [before it], as in the other problem, and we work it out as shown above, whether they are connected or detached. The numerator we get is excluded from the one before it. Then we work that out similarly. The result is the numerator excluded from the one before it. Continue like this to the first [fraction].73 If we wish, we can work it out for disconnected fractions as in the two preceding cases.
143.1 Whenever some of them are disconnected and others are connected, then the connected fractions must be transformed to their disconnected form when writing it down, so that all of them become disconnected. For instance, five sixths less three of its fourths is five sixths less three fourths of five sixths. Now what is written after the “less” is a disconnected fraction.74
143.5 And if there is a whole number before the fractions in a problem, it is multiplied by the denominators and then added with the numerator to become fractions. For example, suppose someone said, “Numerate five and five sixths and three fourths of a sixth”. So we put it down on a line like this:
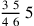 . We multiply the whole number five by the six, the first denominator, and what results by the four, the second denominator. This gives the result one hundred twenty. We add it with the numerator of the fraction, which is twenty-three. This gives a total of one hundred forty-three sixths of fourths, and its figure is 143, which is the numerator.
. We multiply the whole number five by the six, the first denominator, and what results by the four, the second denominator. This gives the result one hundred twenty. We add it with the numerator of the fraction, which is twenty-three. This gives a total of one hundred forty-three sixths of fourths, and its figure is 143, which is the numerator.
143.13 And if it is after them, multiply the numerator by it, since the fractions are portions of it. For example, suppose someone said, “Numerate four sevenths and six eighths of ten”. We put it down on a line like this:
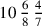 . The numerator of the fractions, as shown before, is seventy-four. We multiply it by the whole number ten to get seven hundred forty sevenths of eighths, which is the numerator, and its figure is 740.
. The numerator of the fractions, as shown before, is seventy-four. We multiply it by the whole number ten to get seven hundred forty sevenths of eighths, which is the numerator, and its figure is 740.
144.4 And if it is in the middle, it is either attached to what is before it, so it is on the end, or it is attached to what is after it, so it precedes it. You numerate it according to one of the two cases, with the remaining [fractions] as distinct in the latter case, and in the former case one multiplies by the numerator of the remaining [fractions].
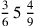 . We multiply the four that is above the nine by the whole number five, giving twenty, which is the numerator of the first part. Then we multiply it by the six, the denominator of the second part, giving one hundred twenty. Keep it in mind. Then we multiply the three, the numerator of the second part, by the nine, the denominator of the first part, giving twenty-seven. We add it with the remembered number to get one hundred forty-seven sixths of ninths, which is the numerator. Its figure is 147.
. We multiply the four that is above the nine by the whole number five, giving twenty, which is the numerator of the first part. Then we multiply it by the six, the denominator of the second part, giving one hundred twenty. Keep it in mind. Then we multiply the three, the numerator of the second part, by the nine, the denominator of the first part, giving twenty-seven. We add it with the remembered number to get one hundred forty-seven sixths of ninths, which is the numerator. Its figure is 147.
145.1 And the “attached to what is after it” [means] that the first fraction is taken of the whole number and of the fraction after it. So the whole number is attached to what is after it, and it precedes it. So you numerate it with it and you multiply that by the numerator of the remaining [fraction], which is the first fraction, since it is a portion of it.
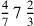 . We multiply the whole number seven by the seven, the denominator of the fraction, and we add the four that is above it and we multiply that by two, the numerator of the remaining [fraction], which is the first fraction. This gives one hundred six thirds of sevenths, which is the numerator, and its figure is 106.
. We multiply the whole number seven by the seven, the denominator of the fraction, and we add the four that is above it and we multiply that by two, the numerator of the remaining [fraction], which is the first fraction. This gives one hundred six thirds of sevenths, which is the numerator, and its figure is 106.
146.3 Common divisors between the numerator and denominators should be removed. We mentioned the way to do this by decomposition in the section on division.76 For portioned fractions in particular one should remove the common divisors before the numeration, since the numbers ascribed to the numerator are above the line and the numbers ascribed to the denominators are below the line. So we drop the repeated [factors] from both of them.77
147.1 Section Two, on adding and subtracting fractions.
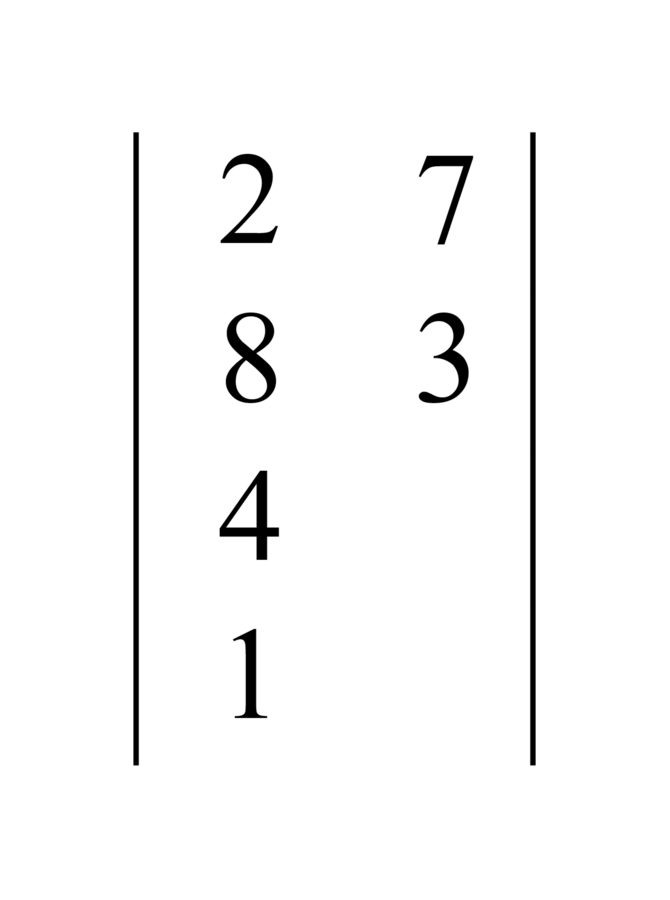
147.2 To work out the addition, you multiply the numerator of each line by the denominators of the other, and you divide the sum by the denominators. And for subtraction you drop the smaller from the greater before dividing by the denominators.
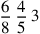
|
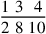
|
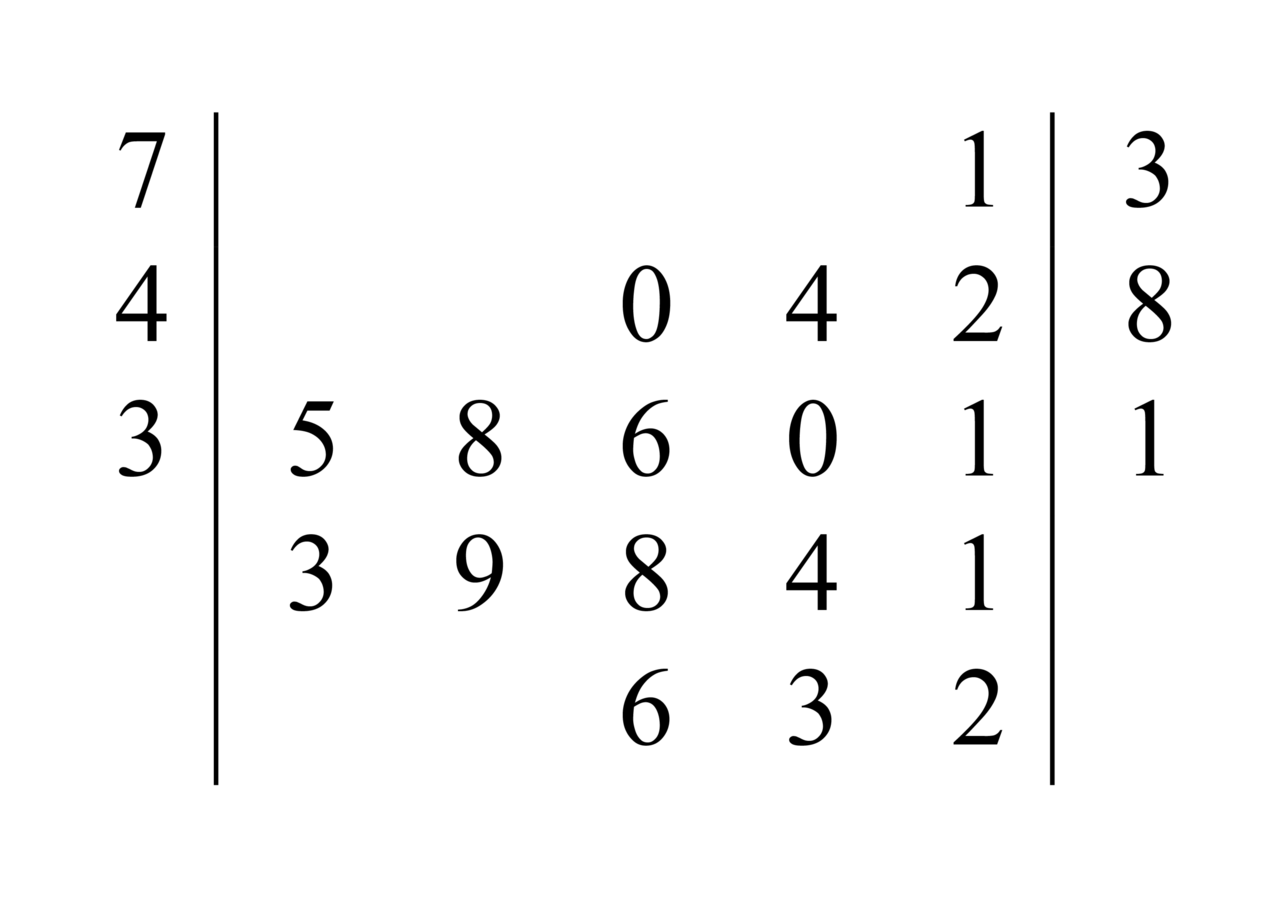
We numerate the upper fraction as before. Its numerator is one hundred eighty-two. We multiply it by the denominators of the lower [fraction], to get twenty-nine thousand one hundred twenty. Keep it in mind. Then we multiply the numerator of the lower [fraction], which is seventy-one, by the denominators of the one above, resulting in two thousand eight hundred forty. We add it with the remembered number to get thirty-one thousand nine hundred sixty, and its figure is 31960. We divide it by the denominators of the two lines. The result is the required number, and that is four and nine tenths and seven eighths of a tenth and half an eighth of a tenth, and its figure is
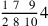 . And its answer is given by five.
. And its answer is given by five.
147.15 Another example, of subtraction: suppose someone said, “Subtract seven tenths of two less a third of one from four and three fourths of five sixths”. We put the minuend down on a line and the subtrahend on another line below it, like with the addend, as in this figure:
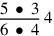
|

|
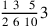 . And its answer is given by subtraction.
. And its answer is given by subtraction.
149.1 Section Three, on multiplying fractions.
149.2 This is the portioning of one of two fractions by the amount of the other. This contrasts with whole numbers or the duplication of fractions by the amount of a whole number. If the multiplier is a whole number and the multiplicand is a fraction, or vice versa, then either one extracts the whole number by the amount of the fraction, or one duplicates the fraction by the amount of the whole number.
149.6 To work it out, that is the multiplication of fractions, you multiply the numerator of each line by the numerator of the other, and you divide the result by the denominators.
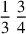
|
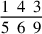
|
We multiply the numerator of the upper [fraction], which is thirteen, by the numerator of the lower [fraction], which is one hundred eleven. It results in one thousand four hundred forty-three, and its figure is 1443. We divide it by the denominators, resulting in the required number, which is four ninths and a fourth of a fifth of a sixth of a ninth, and its figure is
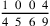 . And its answer is given by one.
. And its answer is given by one.
150.2 Another example: suppose someone said, “Multiply a third of four and an eighth by a fifth of two thirds of ten”. We put the problem down on two lines as before, like in this figure:
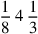
|

|
We multiply the numerator of the upper [fraction], which is thirty-three, by the numerator of the lower [fraction], which is twenty, resulting in six hundred sixty, and its figure is 660. We divide it by the denominators, resulting in the required number, which is one and five sixths, and its figure is
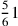 . And its answer is given by two.
. And its answer is given by two.
151.1 Section Four, on division and denomination.
151.2 To work these out you multiply the numerator of each line by the denominators of the other, and you divide the result for the dividend by the result for the divisor, or you denominate.

|
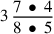
|
We multiply the numerator of the dividend, which is nineteen, by the denominators of the divisor, resulting in seven hundred sixty. Its figure is 760, which is the result for the dividend. Keep it in mind. Then we multiply the numerator of the divisor, which is eighty-four, by the denominators of the dividend, resulting in two hundred fifty-two. Its figure is 252, which is the result for the divisor. We divide the remembered number by it. The result is the required number, which is three and a seventh of a ninth, and its figure is
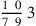 . And its answer is given by four.
. And its answer is given by four.
151.14 Another example, of denomination: suppose someone said, “Denominate three and a fourth less two ninths of it with six and two eighths and three fifths”. We put down the problem as in this figure:
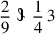
|
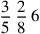
|
We multiply the numerator of the denominated number, which is ninety-one, by the denominators of the denominating number to get the result of three thousand six hundred forty, and its figure is 3640. Keep it in mind. Then we multiply the numerator of the denominating number, which is two hundred seventy-four, by the denominators of the denominated number to get the result of nine thousand eight hundred sixty-four, and its figure is 9864. We denominate the remembered number with it to get the required number, which is fifty parts of one hundred thirty-seven parts and five ninths of a part of one hundred thirty-seven parts, and its figure is
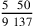 . And its answer is given by subtraction.
. And its answer is given by subtraction.
152.9 When the denominators of the two lines are equal, you divide the numerator by the numerator or you denominate with it, without multiplying by the denominators.

|
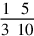
|
We divide the numerator of the dividend, which is two hundred sixty-nine, by the numerator of the divisor, which is sixteen. The result is the required number, which is sixteen and six eighths and half an eighth, as in this figure:
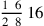 .
.

|
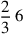
|
We denominate the numerator of the denominated number, which is seven, with the numerator of the denominating number, which is twenty. This results in the required number, which is three tenths and half a tenth, and its figure is
 .
.
153.7 When the two numerators are equal, you divide the denominators of the divisor by the denominators of the dividend, or you denominate, without multiplying by the numerator, since, if we multiply by the denominators, the dividend will be composed from its numerator and the denominators of the divisor, and the divisor will be composed from its numerator and the denominators of the dividend. The two numerators vanish when the common divisors are removed. This is also the cause for the previous method.
154.1 Section Five, on restoration and reduction.
157.1 Section Six, on converting.79
157.2 This section covers two kinds. The intent of one kind concerns only the name, such as when it is said “five sixths and three fourths: how many tenths is it?” We want to denominate these two fractions by naming the fraction in tenths. So we work it out as described, resulting in one and five tenths and five sixths of a tenth, which is what we get from gathering these two fractions together after turning them into tenths. So we shifted the problem from naming in terms of sixths and fourths to naming in terms of tenths and its fractions. This is shifting one kind of fraction to another kind, and it is this kind that is intended in the book.
157.9 The intent of the second kind is: how many of that name, taken as units, are in the whole [fraction]? Work out this kind the same way as for whole numbers. Whenever we want to convert it, we look back to see how it was described in the second type of multiplication.80
158.7 To work this out, that is, the intended kind, you multiply the numerator of the fraction to be converted by the denominator of the converted fraction. One divides the result first by the denominators of the fraction to be converted and then the result by the denominator of the converted fraction. The advantage of this kind is that one can convert a fraction into a finer fraction.
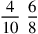
|
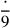
|
We multiply the numerator of the fraction to be converted, which is ninety-two, by the nine, the denominator of the converted fraction, resulting in eight hundred twenty-eight, and its figure is 828. We divide it first by the denominators of the fraction to be converted, then what is left by the denominator of the converted fraction, resulting in the required number. This is one and a ninth and three tenths of a ninth and four eighths of a tenth of a ninth, and its figure is
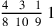 . The same works for similar [examples].
. The same works for similar [examples].
161.1 Chapter Three, on roots. Related to this, we cover what we intend on this topic in four sections.
163.1 Section One, on taking a root of a whole number and a root of a fraction.
163.2 These are divided into two varieties, rational and surd. A rational [root] is any number whose ratio to one is known. This can be a whole number, a fraction, or a whole number and a fraction.
163.4 A surd [root] is one whose ratio to one is unknown. For example, a root of ten, a root of a half, and a root of ten and a half. Surds come in two varieties: those that are expressed with [the word] “root” once, like those just mentioned, and which are called rational in square, and those expressed by “root” more than once, like a root of a root of ten, and which are called medial.83
163.11 In language, it is the origin of everything. He said “root” (jadhr) with a “dh” and either an “a” or an “i” as the vowel for the “j”. Our professor al-shaykh Abū l-ʿAbbās [Ibn al-Bannāʾ], God be satisfied with him, told me that the “a” is more appropriate.
163.14 The ranks in a whole number “have a root” and “do not have a root” for each successive place. This is evident by examination for the units and tens. The hundreds have a root because they come from multiplying the tens by themselves, and the thousands do not have a root because they are in relation to the hundreds in the position that the tens are in relation to the units, and similarly for what comes after that. A place is said to have a root if there is a number in it that has a root.84
164.3 Some conditions for a number may indicate that it does not have a root. But if they do not hold it only implies that it may have a root. These are:
166.1 The way to take a root of a whole number is to count off the ranks with “root”, “no root” to the end of the line. Once you arrive at the last “root”, put a number below it so that if you multiply it by itself, it cancels what is above it or it leaves the smallest possible whole number as remainder. Then you back up, double it, and put it below the place [marked] “no root”. Now you look for a number to put below the “root” preceding it, so that when you multiply it by the doubled number one step back and then by itself, it either cancels what is above it or it leaves the smallest possible remainder. Then if it did not cancel, you do it again. You continue doubling the backed-up number and shifting until you have covered all the line. What you then have in the second line, before doubling, is the root.
166.9 If something remains, denominate it with double the whole part of the root if it is equal to or smaller than the root; and if it is greater than the root, always add one to it, and two to double the root, then you denominate it with it and you add the denomination to the whole part. This gives the root that you multiply by itself, and it is an approximation of a root of the given number.
166.13 For example, suppose someone said, “How much is a root of six hundred twenty-five?” We put it on a line like this: 625. The first place has a root, the second does not have a root, and the third has a root, as mentioned above. We then look for a number to put below the six, which is in a rank that has a root, such that when we multiply it by itself it either cancels the six or it leaves the smallest possible whole number as remainder. We find that it is two. We multiply it by itself, giving four. We drop it from the six, leaving two, which we put in its place. We back up the doubled two and put it below the place [marked] “no root”, which is below the two. Then we look for a number to put below the [rank that] has a root that is before the backed up number below it, and that is below the five. We find it is five. It cannot be anything else.
167.3 So we multiply the five by the doubled four, giving twenty. The twenty-two above its head cancels the twenty, leaving two in its place. Then we likewise multiply it by itself, giving twenty-five, and above its head is twenty-five, which cancels it. The meaning of the five and the doubled two after it is twenty-five, which is the required number. Work it out the same way if there are more digits.
167.8 Another example: suppose someone said, “How much is a root of twenty?” We know that it does not have a rational root since it begins with one zero. We work it out as explained above, and we divide the remainder according to the calculation described above. We look for a number such that when we multiply it by itself, it cancels it or it leaves the smallest possible remainder. We find it is four. We multiply it by itself, giving sixteen. The remainder is four, which is equal to the root. We denominate it with its double, which gives a half. We add it to the whole part of the root, giving four and a half, which is a root of twenty by approximation.
167.14 Another example: suppose someone said, “How much is a root of fifty-four?” We work it out as before, to get seven for the whole part of the root and five for the remainder, which is smaller than the root. We denominate it with its double, giving two sevenths and half a seventh. We add it to the root, to get the sum of seven and two sevenths and half a seventh, which is the required root by approximation.
168.1 Another example: suppose someone said, “How much is a root of ninety-two?” We work it out as before to get nine for the whole part of the root and eleven for the remainder, which is greater than the root. So we add one to it, and two to double the nine, which is the root. We denominate the smaller with the greater and we add it to the root. The result is the required root, which is nine and three fifths. If we multiply the nine and three fifths, which is the approximated root, by itself, it results in ninety-two and four fifths of a fifth. The approximation is found with the added fraction.
168.8 And if you want to refine the approximation, denominate it with double the root. Drop the result from the root, leaving a root whose square is closer to the number whose root is required than the first square.
168.10 He said “denominate it”, by which he meant the fraction added to the square that was found by approximation; because taking the root by approximation can be obtained from a previous close smaller square as seen above, and it can also be obtained from a previous close greater square, which is what he meant when he said “denominate it, etc.”. The description of how to work it out is that we drop the number whose root is required from the square, and we denominate the remainder with double a root of the square, and we also subtract the result from a root of the square. The remainder is a root of the number by approximation.
168.16 If we want to take a root of ninety-two using the previous greater square, we make the greater square ninety-two and four-fifths of a fifth. If we drop the number from it, the remainder will be the fraction found by approximation. So we denominate it with double the root, as mentioned, to get half a sixth of a tenth. We drop it from the root, leaving nine and five-tenths and five-sixths of a tenth and half a sixth of a tenth. A square of this remainder is closer than the first square. So know it.
169.1 There is another method of approximation, which is that you multiply the number whose root is required by a greater square number, and you take a root of the result by approximation, and you divide by a root of the multiplied square. The result is the approximated root.
169.8 The condition “the smallest possible whole number”88 [is needed] because if one diverges from the well-known method by working with fractions, then the remainder will be smaller than the remainder with whole numbers.89
169.10 And suppose someone said, “How much is a root of six hundred twenty-five?” This example is from the earlier problem. We put two and a half below the six, so its square is six and a fourth. This exceeds [the six]. So you take away the six with the six, and take away the fourth with the twenty-five, which is a fourth of a hundred. So all the numbers vanish, and the remainder begins with the last two zeros. We take one of them. Thus the two and a half are tens, which is twenty-five. We double the two and a half to get five, and we place it below the tens. And we look for something to multiply by the doubled number. We find it to be nothing, since there are zeros above it. We put down a zero and we halve what we doubled, so it yields half of fifty.90
169.17 Another example: suppose someone said, “How much is a root of seven hundred twenty-nine?” If we work it out with whole numbers, then the remainder from the seven, which is seven hundred, in its rank is three. And if we work it out with fractions, then the remainder is smaller. So if we put two and a half below it, three fourths of one remains in that rank, and three fourths of a hundred is seventy-five. We add it to the twenty-nine that is with it, to get one hundred four. Then we back up the doubled two and a half, which is five, and we look for a number to multiply by the five and by itself. We find it is two, and nothing remains of the number. So we halve what we doubled, which is fifty. Its half is twenty-five, so the total root is twenty-seven. Or we double the two, so it becomes fifty-four, and we take half of it.91
170.6 Another example: suppose someone said, “How much is a root of a hundred?” The basic rule for this and similar problems is that we always take half of the number of zeros, and we add them to a root of the remaining number to get the root. The hundred begins with two zeros. We take one of them and we add it to a root of the remaining one, giving ten, which is a root of the hundred. So know it.
170.10 To take a root of a fraction, you multiply the numerator by the denominator and you divide a root of the result by the denominator. If the numerator has a rational root and the denominator does too, then divide a root of the numerator by a root of the denominator.
170.14 With regard to taking a root, I mean of a fraction, there are four types. In one of them the numerator has a rational root and the denominator does too. Work it out as described.
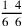 . We take a root of the numerator, giving five. We divide it by a root of the denominator, which is six. The result is the required root, and that is five-sixths.
. We take a root of the numerator, giving five. We divide it by a root of the denominator, which is six. The result is the required root, and that is five-sixths.
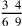 . We multiply the numerator by the denominator to get one thousand four hundred fifty-eight. We take its root, which is thirty-eight and three parts of nineteen parts and half a part of nineteen parts. We divide it by the denominator. The result is the required number, which is thirteen parts of nineteen parts and three ninths of a part of nineteen parts and five-sixths of a ninth of a part of nineteen parts and half a sixth of a ninth of a part of nineteen parts, and its figure is
. We multiply the numerator by the denominator to get one thousand four hundred fifty-eight. We take its root, which is thirty-eight and three parts of nineteen parts and half a part of nineteen parts. We divide it by the denominator. The result is the required number, which is thirteen parts of nineteen parts and three ninths of a part of nineteen parts and five-sixths of a ninth of a part of nineteen parts and half a sixth of a ninth of a part of nineteen parts, and its figure is
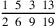 .
.
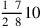 . If we want, we can work it out by the first method. We multiply the numerator by the denominator, resulting in two thousand eight hundred. We take its root, which is fifty-two and forty-eight parts of fifty-three parts and half a part of fifty-three parts. We divide it by the denominator to get the required number, which is three and sixteen parts of fifty-three parts and two eighths of a part and a fourth of an eighth of a part of fifty-three parts, and its figure is
. If we want, we can work it out by the first method. We multiply the numerator by the denominator, resulting in two thousand eight hundred. We take its root, which is fifty-two and forty-eight parts of fifty-three parts and half a part of fifty-three parts. We divide it by the denominator to get the required number, which is three and sixteen parts of fifty-three parts and two eighths of a part and a fourth of an eighth of a part of fifty-three parts, and its figure is
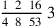 .
.
 . This method is closer than the first [method].
. This method is closer than the first [method].
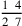 . We multiply the numerator by the denominator and we take a root of the result. This is eleven and two parts of eleven parts and half a part of eleven parts. We divide it by the denominator. The result is the required number, which is eight parts of eleven parts and five sevenths of a part and three fourths of a seventh of a part of eleven parts, and its figure is
. We multiply the numerator by the denominator and we take a root of the result. This is eleven and two parts of eleven parts and half a part of eleven parts. We divide it by the denominator. The result is the required number, which is eight parts of eleven parts and five sevenths of a part and three fourths of a seventh of a part of eleven parts, and its figure is
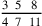 .
.
173.4 To take roots of binomials and apotomes, you drop a fourth of a square of the smaller of the two terms from a fourth of a square of the greater one; you take a root of the remainder, you add it to half of the greater term, and you also subtract it from half of the greater term; and you drop a root on each of them. If the number whose root is required is a binomial, then its root is the sum of these two roots, and if it is an apotome, then its root is the difference between these two roots.
173.10 I say we need to begin with an introduction to clarify binomials and apotomes and how to find them. After that we will take their roots, almighty God willing.
174.1 Roots of the first three binomials and apotomes are closer to being rational in rank than roots of the other three. The first three can be distinguished from the others by multiplying the difference between the squares of the terms by a square of the greater one. If the result is a square, then it is one of the first three, and if it is not a square, then it is one of the second three.
174.14 It is necessary to recall their characteristics if we want to find them. If we subtract a square from a square and the remainder is not a square, and we join a root of the remainder with a root of the greater square, this gives the first binomial. Or we make whatever number we wish the greater term, and [we make] the smaller a root of a surface whose two sides are in numerical ratio,94 with the condition that it is not rational. However, this procedure is rare.
175.11 These are the six binomials. Now let us return to examples of their roots. Example: suppose someone said, “Eight and a root of sixty: how much is a root of that?” We work this out as described. We drop a fourth of a square of a root of the sixty, since it is the smaller, and that is fifteen, from a fourth of a square of the eight, since it is the greater, and that is sixteen. The remainder is one. We take its root, giving one. We add it to half of the eight, since it is the greater, giving five, and we drop it likewise from its half. The remainder is three. We drop a root on the five and the three. This gives a root of five and a root of three, which is the required number. The same rule applies to other [examples].
176.1 Another way to do it is that we drop a square of the smaller term from a square of the greater one, and we take a root of the remainder. We add it to the greater term and we take a root of half of the sum. And likewise, we subtract it from the greater term and we take a root of half of the sum. If the number whose root is required is a binomial, then its root is the sum of these two roots. If it is an apotome, then its root is the difference between the two roots.
176.10 Suppose someone said, “Seven and a root of one hundred twelve: how much is its root?” This is the second binomial. We take its root as before to get, after the addition and subtraction, a root of a root of eighty-five and three fourths and a root of a root of one and three fourths. This is called “the first bimedial”, and its apotome is the second apotome. An apotome of its root is a root of its apotome, and it is called “a first apotome of a medial”.
176.15 Suppose someone said, “A root of thirty-two and a root of fourteen: how much is its root?” This is the third binomial. We take its root as before. This gives, after the addition and subtraction, a root of a root of twenty-four and a half and a root of a root of a half. This is called “the binomial of the second bimedial”, and its apotome is the third apotome. An apotome of its root is a root of its apotome, and it is called “a second apotome of a medial”.
176.20 Suppose someone said, “Seven and a root of thirty: how much is its root?” This is the fourth binomial. We take its root as before, to get three and a half and a root of four and three fourths, taking its root, and three and a half less a root of four and three fourths, taking its root. It is called “the major”, and its apotome is the fourth apotome. And an apotome of its root is a root of its apotome, and it is called “the minor”.
177.5 Suppose someone said to you, “Three and a root of twenty: how much is its root?” This is the fifth binomial. We take its root as before, to get a root of five and a root of two and a half and a fourth, taking its root, and a root of five less a root of two and a half and a fourth, taking its root. It is called “[the number whose] power is a rational and a medial”. Its apotome is the fifth apotome, and an apotome of its root is a root of its apotome. It is called “the joining with a rational to become a whole medial”.
177.11 Suppose someone said, “A root of ten and a root of eleven: how much is its root?” This is the sixth binomial. We take its root as before, to get a half and a root of two and three fourths, taking its root, and a root of two and three fourths less a half, taking its root. It is called “[the number whose] power is a bimedial”. Its apotome is the sixth apotome, and an apotome of its root is a root of its apotome. It is called “the joining with a medial to become a whole medial”.
179.1 Section Two, on adding and subtracting roots of numbers.
179.2 You multiply the two numbers, one of them by the other, when you want to add or to subtract their roots. If the result is a square, then the roots of the two numbers can be added and subtracted. If it is not a square, then they cannot be added or subtracted. If you know they can be added, take two roots of the result and add it to the sum of the two numbers. Take a root of this sum to get the required number.
179.7 For example, suppose someone said, “Add a root of three to a root of twenty-seven”. We multiply the three by the twenty-seven, giving eighty-one, which is a square. We take two of its roots, giving eighteen. We add it to the sum of the two numbers, and a root of that sum is the required number, which is a root of forty-eight.
179.11 Another way is that we divide one of the two addends by the other, we add one to the result, and we multiply the sum by the divisor. The result is their sum.96 So here we divide a root of the twenty-seven by a root of the three, resulting in three. We add one to it, and we multiply the sum by a root of the three, the divisor, as explained [in the section on] multiplying roots.97 This results in a root of forty-eight, which is the required number, as shown above.
179.16 Another example: suppose someone said, “Add a root of two to a root of eight”. We multiply the two by the eight, giving sixteen, and we take two of their roots, giving eight. We add it to the sum of the two numbers, and a root of that sum is the required number, and that is a root of eighteen. If we wish, we can work it out the second way to get the required number.
179.20 Another example: suppose someone said, “Add half a root of twenty to two roots of five”. Half a root of twenty is less than one root, so we transform it to one root, as described in the section on division.98 This gives, according to what was explained on working out the multiplication, a root of five. And two roots of five are more than one root, so we transform them to one root to again get a root of twenty. It is as if someone had said, “Add a root of five to a root of twenty”. We work it out as before to get the required number, which is a root of forty-five.
180.6 Likewise, whenever the roots are of different ranks, we transform them to one rank. For example, suppose the addend is a root of a number rational in square and the augend is a root of a root of a number, that is, a medial. We transform [the number] rational in square to a medial in ratio99 with the other [addend], at which point we add them.100
180.10 Another example: suppose someone said, “Add a root of three to a root of fifteen”. We find that their surface is not a square, so they are incommensurable. We thus add them with the coordinating conjunction to get a root of three and a root of fifteen. Any examples like this, that can only be added with the coordinating conjunction, are called binomials.
180.15 Another example: suppose someone said, “Add half a root of a root of eighty to a third of a fourth of a root of six hundred eighty-four”. It is known, according to what is explained in the section on multiplication,101 that half a root of a root of eighty is a root of a root of five, and that a third of a fourth of a root of six hundred eighty-four is a root of four and three fourths. It is as if someone had said, “Add a root of a root of five to a root of four and three fourths”. We transform them to the same rank, as mentioned before. So the problem becomes as if someone had said, “Add a root of a root of five to a root of a root of twenty-two and four eighths and half an eighth”. Their surface is likewise not a square, so we add them with the coordinating conjunction, and that is a root of a root of five and a root of a root of twenty-two and four eighths and half an eighth. So know it.
181.4 For subtraction, you subtract two of the roots that result from multiplying the two numbers from the sum of the two numbers, and you take a root of the remainder to get the required number.
181.10 Another way to do this is to divide one of the subtrahends by the other. Then take the difference between the result and one, and multiply by the divisor to get the required number.
182.1 If the subtrahend or the minuend is more than one root or less, or if the ranks of their roots are different, then it is necessary to transform them to one root or the same rank, as with addition.
182.4 Another example: suppose someone said, “Subtract a root of eight from a root of ten”. We find that their surface is not a square, so they are incommensurable. So subtract it using the particle of exclusion, and that is a root of ten less a root of eight. Work out [other problems] similarly. So know it. Here, too, any examples like this one that can only be subtracted using the particle of exclusion are called apotomes. So understand it.
183.1 Section Three, on multiplying roots.
183.4 For example, suppose someone said, “Multiply a root of eight by a root of nine”. We multiply the eight by the nine, and a root of the outcome is the required number, which is a root of seventy-two.
183.7 Another example: suppose someone said, “Multiply a root of a root of five by a root of a root of seven”. We multiply the five by the seven, and we drop a root of the root, which the two multiplicands had, on the result. This gives the required number, which is a root of a root of thirty-five. The rule is similar for other medials, no matter how far from rational they are.
183.15 Another example: suppose someone said, “Multiply three by a root of seven less two”. To work this out we multiply the three by a root of the seven, and we subtract from the outcome its multiplication also by the excluded two. The remainder is the required number, which is a root of sixty-three less six. The principle behind multiplying appended and deleted terms will be covered in [the chapter on] algebra,102 with the power of almighty God.
183.20 If you want to multiply a number by a root of a number, square the number and work with the two numbers as shown above.
184.4 Another example: suppose someone said, “Multiply two by a root of a root of three”. We multiply the two by itself, and the result by itself. This is multiplied by the three. A root of a root of the outcome is the required number, which is a root of a root of forty-eight. The rule is similar if there are more [roots] than these. So know it.
184.11 Here is an example with a root that is more than one root. Suppose someone said, “Multiply two by two roots of seven”. It is necessary that we focus on what [makes] this number of a root of the seven a [single] root. To do this we multiply the two, which is the number of the root, by itself, and the outcome by the seven. We take a root of the result, which is the required number, and that is a root of twenty-eight. So it is as if someone had said, “Multiply two by a root of twenty-eight”. We work it out as before, resulting in the required number, which is a root of one hundred twelve.
184.18 Another example: suppose someone said, “Multiply five by three roots of a root of two”. So we likewise focus on what number makes three roots of a root of two a [single] root of a root. To do this we multiply the three, the number of roots, by itself, and the outcome by itself, and the outcome of that by the two, and we take a root of a root of the result. This is the required number, which is a root of a root of one hundred sixty-two. So it is as if someone had said, “Multiply five by a root of a root of one hundred sixty-two”. We work it out as before to get the required number, which is a root of a root of one hundred one thousand two hundred fifty. Work it out similarly if there are more [roots] than these.
185.6 Here is an example with less than one root: suppose someone said, “Multiply two thirds by half a root of twenty”. So we focus on half a root of twenty, and we change it into what [single] root it is, as before. To do this we multiply the half by a root of the twenty, so it gives, as explained, a root of the five. It is then as if someone had said, “Multiply two thirds by a root of five”. We again work it out as before. The result is the required number, which is a root of two and two ninths.
185.12 Another example: suppose someone said, “Multiply a root of five by half a root of a root of forty”. We focus on half a root of a root of forty, and we change it into what root of a root it is, as before. To do this we multiply the half by itself, and the outcome by itself, and the outcome of that by the forty. We get, as we have explained, a root of a root of two and a half. It is then as if someone had said, “Multiply a root of five by a root of a root of two and a half”. We work it out again as before, resulting in the required number, which is a root of a root of sixty-two and a half. Work out similar [examples] the same way.
186.1 Here is an example of duplicating roots: suppose someone said, “Duplicate a root of three twice”. It is as if someone had said, “Multiply two by a root of three”. Work it out as before to get the required number, which is a root of twelve.
186.8 An example of partitioning roots: suppose someone said, “How much is half of a root of ten?” It is as if someone had said, “Multiply a half by a root of ten”. Work it out as before to get the required number, which is a root of two and a half.
187.1 Section Four, on dividing and denominating roots of numbers.
187.2 You divide the number by the number or you denominate it with it, and you take a root of the result. What you get is the result of dividing a root of the dividend by a root of the divisor.
187.10 Work it out similarly for medials. For example, suppose someone said, “Divide a root of a root of six by a root of a root of two”. We divide the six by the two, and we drop a root of the root on the result to get the required number, which is a root of a root of three.
188.1 In these [preceding] three sections, on addition, multiplication, and division, whenever you encounter a term that is more than one root or less than one root, or roots of different ranks, transform them to one root or make them the same rank.
188.6 Along these lines, suppose someone said, “Divide a root of a root of fourteen by a root of two”. The divisor is rational in square and the dividend is medial. So we transform a root of the two so that it is medial like the divisor, and then we divide. We get a root of a root of four. If we divide the dividend by it and we drop a root of the root which the two dividends had on the result, it gives the required number, and that is a root of a root of three and a half.
188.11 Another example: suppose someone said, “Divide two roots of fifteen by two”. We already knew that two roots of fifteen are the same as a root of sixty, and that the two is a root of four. So it is as if someone had said, “Divide a root of sixty by a root of four”. We work it out as before to get the required number, which is a root of fifteen.
188.18 For division by binomials and apotomes, you multiply the dividend and the divisor by an apotome of the divisor if it is a binomial, or by its binomial if it is an apotome. Then you divide the result of the dividend by the result of the divisor.
191.1 Part Two, on the basic rules by which one arrives at knowledge of the required unknown from the posited known.
193.1 Chapter One, on working out [problems] with proportion. This can be done in two ways, with four proportional numbers and with scales.
195.2 I say there are different kinds of proportions. Among them are arithmetical, harmonic, harmony, and ex-aequali proportion. For arithmetical [proportion], its principles have already been covered,104 and for the other three, they are not described.105 As mentioned, they are dispensable, since they originate from it, and it is the foundation of calculation. All three derive from it and it does not derive from them, as was shown in Lifting the Veil.106
195.7 Four proportional numbers are those for which the ratio of the first to the second is as the ratio of the third to the fourth, and the product of the first by the fourth equals the product of the second by the third.
195.9 Whenever you multiply the first by the fourth and you divide by the second, it results in the third; or by the third, it results in the second. And whenever you multiply the second by the third and you divide by the first, it results in the fourth; or by the fourth, it results in the first. Whichever is unknown can be worked out from the other three known numbers.
195.14 The way to do this is that you multiply the isolated number different in kind from the others by the number in ratio with the unknown, and then you divide by the third number, resulting in the unknown.
195.16 For example, the ratio of three to six is as the ratio of four to eight. So the three with respect to the six is a half, and the four with respect to the eight is a half. The product of the first, which is the three, by the fourth, which is the eight, equals the product of the six, which is the second, by the four, which is the third.
196.16 For the four proportional numbers, if one switches to get the ratio of the first to the third and the second to the fourth; or reverses them to get the ratio of the second to the first and the fourth to the third; or combines to get the ratio of the sum of the first and the second to one of them is as the ratio of the sum of the third and the fourth to one of them; or separates to get the ratio of the difference between the first and the second to one of them is as the ratio of the difference between the third and the fourth to one of them; or combines after switching them; or separates after switching them; or switches after combining them; or switches after separating them; or reverses after any one of these, they will remain proportional.108
197.4 There are four ways to find the unknown other than those mentioned. First, if the fourth, for example, is unknown, we divide the second by the first, and we multiply the result by the third, to get the fourth. Second, we divide the third by the first, and we multiply the result by the second, to get the fourth. Third, we divide the first by the second, and we divide the third by the result, to get the fourth. Fourth, we divide the first by the third, and we divide the second by the result, to get the fourth. These are not presented by the author because what he presented is the source of all of them. They derive from it, and it does not derive from them. As the jurist Abū Muḥammad ʿAbd al-Ḥaqq ibn Ṭāhir reported, the first way is called the procedure, and the other four are called deductions by analogy.
198.2 The [method of] scales comes from the art of geometry. It comes from the art of geometry because the ratio of the error of each scale to the difference between the scale and the unknown number is as the ratio of the assigned number to the unknown.109
198.4 You switch, you separate, you switch. The ratio of the portion to its scale is as the ratio of the assigned number to the unknown, as was made clear in Lifting the Veil.110
198.7 You represent this by drawing a balance, as in this figure:111
199.1 For example, suppose someone said, “A quantity: taking away its third and its fourth leaves ten. How much is the quantity?”
200.1 Another example: suppose someone said, “A quantity: we take the sum of its third and its fifth, and we add to it half of the remainder, so it comes to twenty-three. How much is the quantity?”
201.1 Another example: suppose someone said, “A quantity: we add its tenth to the difference between its fourth and three of its fifths, so it comes to nine. How much is the quantity?”
201.14 If you wish, you can choose the first number or any other number for the second scale, then figure its portion, which you confront with what is above the dome. Multiply it by the first posited number, and multiply the first error by the second posited number. If the first error falls short, you add the two products. If it exceeds, you take their difference. You divide the result by the portion of the second scale to get the required number.
202.3 This second method is used only when there is a proportional relation. For example, suppose someone said, “Ten: you divide it into two parts so that a third of one of them is a fourth of the other”.114
203.1 Another example: suppose someone said, “Ten: you divide it into two parts. You divide the greater by the smaller, so the result is four. How much is one of them?”
203.11 We follow the second method in any problem where the assigned numbers are one of the scales and its error. For example, I say, “A quantity: we subtract its third and its fourth from a third of sixty and its fourth, leaving fourteen. How much is the quantity?”
204.3 Regarding this, my professor, the jurist and great erudite Abū l-ʿAbbās [Ibn al-Bannāʾ], God bless him, dictated to me while I was studying with him on Wednesday, the twenty-eighth of the month of rajab in this year:
204.6 “There are three approaches. One of them is that you multiply the difference between the scales by one of the errors. If the two errors both exceed or both fall short, you divide the product by their difference. If one of them exceeds and the other falls short, you divide the product by their sum. You add the result of this to the scale whose error you multiplied if it falls short, and you subtract it from it if it exceeds. This gives the required number.
204.12 “The second approach is that you multiply the difference between the scales by the sum of the errors if they both exceed or both fall short, and you divide by their difference. If one of them exceeds and the other falls short, you multiply the difference between the scales by the difference between the errors, and you divide by the sum of the errors. Keep this result in mind. If you wish, you add this remembered number to the difference between the scales and you take half of the sum. You add it to the scale whose error is greater if it falls short, and you subtract it from it if it exceeds, to get the required number.
205.1 “The third approach is that you multiply the difference between the scales by your assigned number. If the errors both exceed or both fall short, you divide the product by their difference, and if one of them exceeds and the other falls short, you divide the product by their sum, to get the required number. So know it.”
205.5 Scales can also be set up to find the unknown in cases without a proportional relation, as in this problem: Three men want to buy a horse.116 The first says to the second, give me half of what you have, and, together with what I have, I will have the price of the horse. The second says to the third, give me a third of what you have, and, together with what I have, I will have the price of the horse. And the third says to the first, give me a fourth of what you have, and, together with what I have, I will have the price of the horse.
206.5 If we wish the result to be without fractions, we multiply all of the problem by the smallest number divisible by their denominators. We knew [how to do] this before,118 and it is four. By this calculation the first has sixteen, the second has eighteen, the third has twenty-one, and the price of the horse is twenty-five. So understand it.
207.1 If we [choose to] assign the price of the horse, we put it above the dome, and we put some portion of it for the first [man], and twice its remainder for the second. Then we drop a fourth of what we put for the first from the price of the horse, leaving what the third has. Then we take what the second has and a third of what the third has, and we confront it with the assigned price. We then do this likewise for the other scale: we first make the price of the horse whatever we wish, as long as it is not the first number. Then we work it out as before.
207.6 Another problem: forty birds, among which are geese, chickens, and starlings, [all] for forty dirhams. The starlings are eight for a dirham, the chickens are one for two dirhams, and the geese are one for three dirhams. How many were chosen of each kind of bird?
207.9 Not all examples of this type can be worked out. Two conditions must be satisfied. One is that the numbers must be whole numbers and not fractions. Second, the price of one of the cheapest [birds], if multiplied by the number of birds, must be smaller than the total price; and the price of one of the most expensive [birds], if multiplied likewise, must be greater than the [total] price.
208.12 If we make the starlings thirty-two, it is not valid since the condition for the remaining [birds] is not met. Thus this problem has only one answer. For similar problems, look to these two problems. Problems like this cannot be worked out by the second method of solving by scales, since that is specific to a proportional relation, as said above. Problems involving multiplication are not based in proportion, so they cannot be solved by the scales. So know it.120
209.1 Chapter Two, on algebra. We present this work in five sections.
211.1 Section One, on the meaning of algebra (restoration and confrontation) and an explanation of its types.121
211.2 Restoration is the reconstitution we mentioned in Part One of this book.122 Confrontation is subtracting each species from like [species] until there are no longer two species of the same kind in the two parts.123 And equalization is the restoration of the deleted to the appended, and the subtraction of the appended from the appended and the deleted from the deleted of things of the same kind. This will be covered with clear examples in the section on addition and subtraction,124 almighty God willing.
211.8 Algebra depends upon three species: the number, the things, and the māls. The things are roots, since every unknown in numbers is a thing, and a root of its square when it is known. The māl is what one gets from multiplying the root by itself. The term māl serves to distinguish it from the other [species].
211.13 These three species are equated to one another, in either a simple or composite way. This results in six types, three simple and three composite.
213.1 Section Two, on working out the six types.
213.2 For the three simple [types], you divide by the māls what they are equal to, and by the roots if there are none. The result of the division in the first and third types is the root, and in the second it is the māl. If the root is known, then the māl is known by multiplying the root by itself. And if the māl is known, then the root is known from it.
213.7 For example, suppose someone said, “Three māls equal fifteen things”. The meaning of this problem is: what quantity (māl), if we take its root fifteen times, gives a sum equal to three times the quantity? This is of the first type, and it is worked out as explained above. If we divide the fifteen, the number of things, by the three, the number of māls, it results in five, which is a root of the unknown māl, the latter being twenty-five.
213.13 Another example: suppose someone said, “Two māls equal eighteen”. The meaning of this problem, likewise, is: what quantity (māl), if we add itself to it, becomes equal to eighteen? This is of the second type. To work it out we divide the eighteen by the two, the number of māls, as mentioned, to get nine. This is the unknown māl, and its root is three.
214.1 Another example: suppose someone said, “Five things equal twenty”. The meaning of this problem, likewise, is: what quantity (māl), if we take five of its roots, gives a result equal to the twenty? This is of the third type. To work it out we divide the twenty by the five, the number of things, since there are no māls. It results in four, which is a root of the unknown māl, and that is sixteen.
214.7 To work out the fourth type, you halve the number of roots, you square the half, you add it to the number, you take a root of the result, and you drop the half from it, leaving the root.
214.9 For example, suppose someone said, “A māl and two things equal fifteen”. Its meaning is, what quantity (māl), if we add two of its roots to it, becomes equal to fifteen? We take half of the things, giving one, and we square it, giving one, and we add the number to it, giving sixteen. We take its root, giving four. From this we drop the one, which is the half, leaving three. This is the unknown thing, and the māl is nine.
214.14 If we wish to find the māl first, before the root, we add half a square of the number of roots to the number, then keep the sum in mind. Then we subtract a square of the number from a square of the remembered number, and we take a root of the remainder. We subtract this from the remembered number. The remainder is the māl.
215.3 For the fifth [type], you subtract the number from a square of half of the number of roots, and you take a root of the remainder. If you add it to the half, it gives a root of the greater māl, and if you subtract it, it gives a root of the smaller māl.
215.12 Know that whenever a square of the half is equal to the number, then the half is the root, and the māl is the number.
215.14 For example, suppose someone said, “A māl and nine equal six things”. We square half of the things, giving nine, and this is equal to the number. So the number is the māl, and the half is the root. And if we continue the solution, we subtract the number from the square, leaving nothing. We take its root, giving nothing. We add nothing to the half, or we subtract it from it, leaving the half. It is the root, and its square is the number. So know it.
216.1 If we wish to find the māl first, before the root, we subtract the number from half of a square of the number of roots, and we keep the remainder in mind. Then we subtract a square of the number from a square of the remembered number. If we add a root of the remainder to the remembered number, it gives the greater māl; and if we subtract it from it, then the remainder is the smaller māl. Note that this is what it is when the number is smaller than a square of half of the number of roots.
216.11 The sixth [type] is solved like the fourth, except that you add the half at the end to a root of the sum to get the root.125
216.17 If we wish to find the māl first, before the root, we add double the number to a square of the roots, and we keep half of the sum in mind. Then we drop a square of the number from a square of the remembered number, and we add a root of the remainder to the remembered number. This gives the māl.
217.1 For each of the three composite types, whenever there is more than one māl, reduce it to one māl, and reduce by that term all of the equation. And for each of them, whenever there is less than one māl, restore it to one māl, and restore by that term all of the equation. The way to work out restoration and reduction was described earlier.126 And if you wish, divide [each of] the names127 in the problem by the number of māls. This reduces the problem.128 Then confront the two sides.
217.10 For example, suppose someone said, “Two māls and six things equal thirty-six”. We reduce the two māls to one māl by multiplying them by a half, as mentioned above. And we reduce by this [multiplication] the things and the number. So the problem becomes: a māl and three things equal eighteen, which is the fourth type. This is also how to work out the fifth and sixth [types].
217.15 And if we work it out the other way, we divide the two, the number of māls, by itself, resulting in one. And we also divide the number of things by it, resulting in three. And we also divide the number by it. So the problem becomes: a māl and three things equal eighteen, just as before.
218.1 Another example: suppose someone said, “Half a māl and two things equal six”. We restore the half to one māl by multiplying it by two. We multiply it also by the things and the number. So the problem becomes: a māl and four things equal twelve, which is also the fourth type. This is also how to work out the fifth and sixth [types].
219.1 Section Three, on addition and subtraction.
219.2 Adding different species is done with the conjunction “and”, like: a māl and six things and ten dirhams.129
219.4 …and the different excluded [species] cannot be subtracted.
219.5 For example, suppose someone said, “Add a māl less a thing to ten dirhams”. The sum is: a māl and ten dirhams less a thing. So the exclusion remains as it was, since [the thing] cannot be subtracted from anything.130
219.7 Whenever appropriate, subtract the smaller from the greater, that is, in the problem. For example, suppose someone said, “Add two māls less a māl to ten dirhams”. So we subtract the excluded māl from the two māls, so the remaining sum is a māl and ten dirhams.
220.1 Subtracting different species is done using the particle of exclusion. For example, suppose someone said, “Subtract a thing from a māl”, then the remainder is a māl less a thing.
220.5 The exclusion can be in both parts133 or in one of them, and it might be one species or two different species. To work it out, you add the exclusion in each part to both parts at once, and then you subtract. Work out the two sides of an equation similarly whenever they have exceptions.
220.9 For example, suppose someone said, “Subtract two and a thing from a māl less three things”. We find the things on the side of the minuend to be deleted, and they are three. We add them to the two parts at once. This is what is meant by equalization with restoration, since we added to the māl what it is associated with, which are the three things. Thus we restore it from deleted to appended. It becomes greater, as is desired for the minuend. We [also] equalize by restoring the subtrahend by the amount we added in the minuend, which is by the three things, since subtracting two numbers is the same as subtracting them after having added a number to both of them, or after subtracting a number from both of them. The problem is as if someone had said: “Subtract two and four things from a māl”. Then we work it out as before. The remainder after that is the required number, which is a māl less four things and less two. So know it.
221.1 Another example of this: suppose someone said, “Subtract fifty-two dirhams less five things from two cubes and thirty dirhams”. We find the things on the side of the subtrahend to be deleted, and they are five. We add them to the two sides at once, as before. The problem becomes as if someone had said: “Subtract fifty-two dirhams from two cubes and five things and thirty dirhams”. Then we find dirhams on both sides. We remove the smaller quantity from the two sides at once. The problem becomes as if someone had said, “Subtract twenty-two dirhams from two cubes and five things”.
221.8 This is confrontation with equalization, since when we removed the thirty from the subtrahend it becomes smaller than the original subtrahend. So we equalize, by which we remove from the minuend the same amount we removed from the subtrahend. It is worked out like before. We work the remainder as before. What remains after that is the required amount, which is two cubes and five things less twenty-two dirhams.
221.13 Another example: suppose someone said, “Subtract twelve dirhams less four things from three māls less two things”. We find two deleted things in the minuend, and also four deleted things in the subtrahend. We add them. Since they are of the same species, they amount to six things. We add them to the two parts at once, or we restore both the subtrahend and the minuend by what is excluded from them, and we add their equals to the other [part], as before. The problem becomes as if someone had said, “Subtract twelve dirhams and two things from three māls and four things”. So we confront and subtract. The remainder after that is the required number, and that is three māls and two things less twelve dirhams.
222.1 Another example: suppose someone said, “Subtract a cube less two māls from thirty dirhams less four things”. We restore and subtract. The remainder is the required number, which is thirty dirhams and two māls less a cube and less four things.
223.1 Subsection concerning examples with the two sides of an equation.
223.2 Along these lines, suppose someone said, “A māl less three things equal two and a thing”. We find the things on the side of the māl to be deleted, and they are three. We restore the māl by them, and we also add them to the two sides of the equation134 as we did before, since whenever one adds equals to equals or subtracts equals from equals, the outcomes are equal. So the problem becomes: a māl equals two and four things, which is the sixth type.
223.7 Another example: suppose someone said, “A māl less three things equal twenty-four dirhams less five things”. We restore and confront as before, so the problem becomes: a māl and two things equal twenty-four dirhams, which is the fourth type. If we wish, we can first subtract the three things which are deleted on the side of the māl from the five things deleted on the side of the number. This leaves two things deleted on the side of the number. And we finish working it out, again arriving at the fourth type.
223.14 Another example: suppose someone said, “A māl less ten dirhams equal a māl less two things and a half”. We restore and confront, so the problem becomes: ten dirhams equal two things and half a thing, which is the third type.
223.17 Another example: suppose someone said, “A māl and ten dirhams equal fifty-one dirhams less four things”. We restore, and the problem becomes: a māl and four things equal forty-one dirhams, which is the fourth type.
225.1 Section Four, on multiplication and knowing the power and the term.
226.1 Conversely, suppose someone said, “What is a term for four?” We would say a māl māl. And if someone said, “What is a term for seven?” We would say a cube māl māl. And if someone said, “What is a term for six?” We would say a māl māl māl, or a cube cube.
226.9 To multiply these species, add the power of the multiplicand and the power of the multiplier. Then the sum of the powers is the power of the result. To multiply a number by one of these species, the result is the same species.
226.12 For example, suppose someone said, “Multiply five things by seven things”. We multiply the number of the multiplicand, which is five, by the number of the multiplier, which is seven, giving thirty-five. Then we add the powers of the two multiplicands, giving two. This two is the power of the thirty-five resulting from the multiplication, so it is māls. So the result of the multiplication is thirty-five māls, which is the required number.
227.10 Another example: suppose someone said, “Multiply seven by three māls cube”. We multiply the multiplicand by the number of the multiplier, giving twenty-one. The outcome of the multiplication in this example is likewise māl cube, so it is then twenty-one māls cube. So know it.
227.14 Whenever you equate between the māls māls and the cubes and the māls, or the cubes and the māls and the things, or any combination in which you do not have a number, subtract the smaller of the powers from the power of each of them. Then you equate what remains, one with the others, in the same way as the equation.
228.8 If it is not possible to transform it to [one of] the six types, then do not work it out since it would be of no use for anything.
228.9 The multiplication of two appended or deleted [terms], one of them by the other, is appended, and the multiplication of an appended [term] by a deleted [term] is deleted.
228.15 Another example: suppose someone said, “Multiply eight less two things by seven less four māls”. We multiply the appended eight by the appended seven, to get an appended [amount]. We add to it the product of the two deleted things by the four deleted māls, since it is appended. And we drop from the sum the product of the appended eight by the deleted four māls, since it is deleted, and the product of the deleted two things by the appended seven, since it is deleted. The remainder, then, is the required [number], and that is eight cubes and fifty-six less fourteen things and less thirty-two māls. So know it.
229.1 Section Five, on division.
229.2 To divide one of these species by a lower species, drop the power of the divisor from the power of the dividend. What remains is the power of the species of the result of the division.
229.8 Another example: suppose someone said, “Divide fifteen cubes by three things”. We divide the number of cubes by the number of things, and we call the resulting five by the name for the difference between the power of the things and the cubes, and that is a māl. The resulting five is then five māls, which is the required amount. So know it.
229.12 And whenever you divide a species by itself, the result is a number.
229.17 For example, suppose someone said, “Divide twelve things by four dirhams”. We divide the number of the dividend by the number of the divisor, resulting in three. And the number of the divisor has no power, so that dropping from the power of the dividend leaves the power of the dividend as the power of the result, so we call it with its term. The result is three things, which is the required number.
230.1 If there is an exclusion in the dividend, divide both the excluded [term] and the diminished [term] by the divisor, and exclude the result of the excluded [term] from the result of the diminished [term]. The outcome of this is the result of the division.
230.11 One cannot divide the lower of two species by the higher except by cancelling their common divisor, by which you subtract the power of the smaller from the powers of both of them.
230.16 And one cannot divide by a diminished [term]. So understand it and figure it out with the help of God.
231.1 Section [on secret numbers].
231.4 One of them is that we tell someone to drop his [secret] number from ten, then to drop a square of the remainder from a square of his number. If [a square of] the remainder is smaller, we ask for the remainder. We divide it by ten, and we add ten to the result and then take half of the sum137 to get the secret number. And if a square of the remainder is greater, he drops a square of the secret number from it, and we ask for the remainder. We divide it by the ten, and we drop the result from ten. Half of the remainder is the secret number. If we wish, we can ask that he drop his secret number from something other than the ten. Following the procedure will give the required number.
231.13 The second problem. We tell someone to divide the ten into two parts secretly. Then we tell him to divide a square of one of them by their surface, and we ask for the outcome. If we knew this, it is the ratio of one of the two parts to the other. So we divide the ten according to this ratio. And similarly, we can work with whatever number we wish other than the ten, dividing it secretly. This results in the two secret parts.
232.1 The third problem. A secret number is divided into two secret numbers. How much is it? And how much are each of its parts? We tell him to multiply one of the parts by the other and to square each of them, then to drop a square of the smaller from a square of the surface, and we ask for the remainder; and to drop the surface from a square of the greater, and we ask for the remainder. We take a root of the difference between the two asked numbers, which is the difference between the parts. Then we divide the sum of the asked numbers by it to get the secret number, which is the sum of the two parts. If we add to it a root of the difference between them, it gives double the greater, and if we subtract it from their sum, it leaves double the smaller. So know it.
233.2 As the servant [of God], the named, the tempted, ʿAbd al-ʿAzīz ibn ʿAlī ibn Dāwud al-Hawārī al-Miṣrātī, may God have mercy on him, said: With the praise of God for His excellent assistance, I have achieved what I set out to accomplish to the extent of my ability, and not absolving myself of my errors and of anything leading to wrong ideas, I beg Almighty God’s protection and to preserve me from loosing His favors. He is sufficient for us, and He is the best disposer of our affairs.
This work was completed on Saturday, the eighteenth of Dhū al-Qaʿda, 704. May God’s generosity benefit the author. Full prayers upon His prophet and servant, our Master and Lord Muḥammad, and upon his family and companions and followers.
Footnotes
I.e., calculating a cube root.
Ibn al-Bannāʾ.
Copied from (Ibn al-Bannāʾ 1994, 212.9-10).
Literally, “Number has twelve simple names from which all of its names are formed”.
From here to the end of the section we write the numbers in the order they are written in Arabic, and with the stated plurals of “thousand”. Unlike thousands, hundreds are not made plural when there is more than one because the numbers “two hundred”, “three hundred”, up to “nine hundred” are single compound words in Arabic. After that, we switch back to the English order, and without the plural.
They are only units, since there is only a 9.
I.e., a number expressed with a repetition of the word “thousands”.
Literally, “tens thousands thousands thousand” and “hundreds thousands thousands thousand”.
Copied from Ibn al-Yāsamīn, (Zemouli 1993, 131.2-5).
Copied from (Ibn al-Bannāʾ 1994, 214.3-5).
Copied from (Ibn al-Bannāʾ 1994, 214.13-15).
Copied from (Ibn al-Bannāʾ 1994, 214.18-215.1).
Copied from Ibn al-Yāsamīn, (Zemouli 1993, 131.5-8).
Copied from (Ibn al-Bannāʾ 1994, 226.5-7).
Copied from Ibn al-Yāsamīn, (Zemouli 1993, 131.9-14).
Copied from Ibn al-Yāsamīn, (Zemouli 1993, 131.15-16).
I.e., the units in a particular rank are the tens for the rank before it.
Copied from Ibn al-Yāsamīn, (Zemouli 1993, 131.17).
Ibn al-Bannāʾ copied 76.7-12 from Ibn al-Yāsamīn, (Zemouli 1993, 132.1-6).
I.e., double the number of squares, like from the fourth square to the eighth square.
I.e., the sum of their indexes.
This sentence is copied from Ibn al-Yāsamīn, (Zemouli 1993, 136.6).
Copied from Ibn al-Yāsamīn, (Zemouli 1993, 136.7-9).
Copied from (Ibn al-Bannāʾ 1994, 220.8-12).
This passage belongs in the Condensed Book, but it is not in Souissi’s edition. It is copied from Ibn al-Yāsamīn, (Zemouli 1993, 136.9-12).
Copied from Ibn al-Yāsamīn, (Zemouli 1993, 136.13-14).
Copied from (Ibn al-Bannāʾ 1994, 228.13-15).
The Medina and Oxford manuscripts show
![\begin{matrix}{3074}\\[-.5mm]6543\\[-.5mm]3469\end{matrix}](../../../media/sources/14/4/EOAineq_4_10.png) .
.
Literally, “working out”.
Copied from (Ibn al-Bannāʾ 1994, 245.8-15).
Copied from (Ibn al-Bannāʾ 1994, 245.16-247.2).
I.e., the nine, called “ninety” here because it is positioned one place forward.
Copied from (Ibn al-Bannāʾ 1994, 248.11-17).
Copied from (Ibn al-Bannāʾ 1994, 248.18-249.4).
Copied from (Ibn al-Bannāʾ 1994, 249.5-11). Ibn al-Bannā gives a section on numeration in Lifting the Veil at p. 272.14. Al-Hawārī covers numeration beginning at 135.8.
Copied from (Ibn al-Bannāʾ 1994, 255.3-13).
We translate as “last digit” what is more literally “what is in the last rank”.
This is misstated. The multiplier, not the three, is shifted.
Copied from Ibn al-Yāsamīn, (Zemouli n.d., 15.2-9).
The reference is to (Ibn al-Bannāʾ 1994, 215.12).
The three is already there, so there is no need to write it.
I.e., divide it by 10.
Copied from Ibn al-Yāsamīn, (Zemouli n.d., 16.5-7).
Copied from Ibn al-Yāsamīn, (Zemouli n.d., 16.8-13).
Copied from Ibn al-Yāsamīn, (Zemouli n.d., 16.14-17.2).
Copied from Ibn al-Yāsamīn, (Zemouli n.d., 17.3-7).
Copied from Ibn al-Yāsamīn, (Zemouli n.d., 17.8-10).
Copied from Ibn al-Yāsamīn, (Zemouli n.d., 17.11-13).
Copied from Ibn al-Yāsamīn, (Zemouli n.d., 17.13-15).
Copied from Ibn al-Yāsamīn, (Zemouli 1993, 119.13-14).
Copied from (Ibn al-Bannāʾ 1994, 263.3).
Copied from Ibn al-Yāsamīn, (Zemouli 1993, 119.16).
Copied from (Ibn al-Bannāʾ 1994, 263.4).
Copied from (Ibn al-Bannāʾ 1994, 263.4-9).
Copied from (Ibn al-Bannāʾ 1994, 263.10-264.8).
Copied from (Ibn al-Bannāʾ 1994, 266.15-20).
Copied from (Ibn al-Bannāʾ 1994, 267.1-5).
Copied from (Ibn al-Bannāʾ 1994, 267.11-14).
The text mistakenly has “a square of the dividend”.
Copied from (Ibn al-Bannāʾ 1994, 272.14-273.19).
Copied from (Ibn al-Bannāʾ 1994, 275.8-9).
The coordinating conjunction is the word “and” (wa).
Copied from (Ibn al-Bannāʾ 1994, 275.14-16).
Copied from (Ibn al-Bannāʾ 1994, 276.3-5).
Copied from (Ibn al-Bannāʾ 1994, 276.16-277.2).
Copied from (Ibn al-Bannāʾ 1994, 277.4-6).
Copied from (Ibn al-Bannāʾ 1994, 279.15).
Everything from 157.2 to 158.6 is slightly condensed from (Ibn al-Bannāʾ 1994, 279.18-280.20).
Copied from (Ibn al-Bannāʾ 1994, 279.18-280.12).
Copied from (Ibn al-Bannāʾ 1994, 280.16-20). Al-Hawārī added “by the author” and changed Ibn al-Bannāʾ’s “I mentioned” to “he mentioned”.
Copied from (Ibn al-Bannāʾ 1994, 283.3-7).
Copied from (Ibn al-Bannāʾ 1994, 283.8-11).
I.e., the parity of half of the tens digit is different from that of the hundreds digit.
Copied from (Ibn al-Bannāʾ 1994, 284.14-285.1).
Copied from (Ibn al-Bannāʾ 1994, 285.2-285.6).
Copied from (Ibn al-Bannāʾ 1994, 283.11-12).
Copied from (Ibn al-Bannāʾ 1994, 284.4-9).
Copied from (Ibn al-Bannāʾ 1994, 283.13-284.3).
The coordinating conjunction is the word “and” (wa).
The particle of exclusion is most often the word “less” (illā).
I.e., they are commensurable.
Copied from (Ibn al-Bannāʾ 1994, 287.19-288.19).
Judging by the corresponding passage at 181.10, this sentence should have been attributed to Ibn al-Bannāʾ. It is not in the Condensed Book, so it should be in small caps.
I.e., commensurable.
Judging by the passage at 182.1, this passage should have been attributed to Ibn al-Bannāʾ. It is not in the Condensed Book, so it should be in small caps.
I.e., in Ibn al-Bannāʾ’s Condensed Book.
(Ibn al-Bannāʾ 1994, 293.17). By “as mentioned” he means “as mentioned in Lifting the Veil”. See our commentary at 195.2.
Copied from (Ibn al-Bannāʾ 1994, 294.3-9).
Copied from (Ibn al-Bannāʾ 1994, 297.17-18).
This is the only figure in Ibn al-Bannāʾ’s Condensed Book.
That is, the same calculation with the scales reversed.
Copied from (Saidan 1986, 557.7).
Copied from (Ibn al-Bannāʾ 1994, 298.13-19).
The word dābba means a “riding animal”, such as a horse, mule, or donkey. We translate it as “horse”.
Copied from (Ibn al-Bannāʾ 1994, 299.1-14).
Copied from (Ibn al-Bannāʾ 1994, 299.15-300.17).
Copied from (Ibn al-Bannāʾ 1994, 300.18-22).
I.e., in the two parts of a subtraction, or in the two sides of an equation.
By “names” (here alqāb) he means the terms of the equation.
Literally, “what results is a returning to the problem”.
Copied from (Ibn al-Bannāʾ 1994, 313.3).
Copied from (Ibn al-Bannāʾ 1994, 313.3-5).
Copied from (Ibn al-Bannāʾ 1994, 313.6-9).
Copied from (Ibn al-Bannāʾ 1994, 313.10-11), except that Ibn al-Bannāʾ solves “add a māl less ten things to five things”.
That is, in the minuend or the subtrahend.
He should add them only to the side with two and a thing, because the act of restoration already adds them to the māl.
Literally, “there is nothing between the powers”.
Literally, “we name the name”, with ism.
This sentence is our reconstruction of what appears to be a corrupt passage. Literally, it reads “We divide it by ten, and what results, we add to it half of its remainder to the ten”. Only the Oxford manuscript attempts to correct it, by writing “We divide it by ten, and what results, we add to the remainder from the ten”. This is mathematically correct, but we cannot add the remainder from the ten because that is not revealed to us. This MS also has “square” scratched in above “remainder”.