One of the most challenging aspects of Benedetti’s endeavor was his attempt to merge mathematical and physical speculations, as is clearly stated in the title of the Diversae speculationes mathematicae et physicae. In order to understand his way to “physico-mathematics,” we will discuss his mathematical epistemology starting from some statements scattered in his major work and then look at the premises implicit in his treatment of nature. We will briefly review the Renaissance reflections on mathematics linked to practical developments in technological fields as well as to eclectic reassessments of Pythagorean and Aristotelian debates on the certainty of mathematics and their applicability to natural philosophy. Focusing on the epistemological premises underlying Benedetti’s mechanics, we will discuss medieval and early modern approaches to natural knowledge, which, in spite of their mathematical rigor, rested on a physics and metaphysics of contingency. For many centuries, it was assumed that the mathematical regularity of the phenomena does not imply their causal necessity.
4.1 The Certainty of Mathematics
In the letter to the Venetian
I am surprised that, although you are well-versed in Aristotelianphilosophy, nonetheless you make a distinction between the philosopher and the mathematician in your writings, as if the mathematician were not as much a philosopher as the naturalist and the metaphysician. In fact, as far as the certainty of his conclusions is concerned, he deserves the title of philosopher much more than them.1
This reference to mathematical conclusiones reveals Benedetti’s methodological focus on the dignity and validity of his discipline. In his connection of mathematical and physical speculations, he seems to put the emphasis on the method rather than on ontology and to seek for the certainty of mathematics and its applications by way of its specific logic. This was the position of his correspondent, the Paduan
Actually, you are not the only one who makes this mistake, but this is more grave in consideration of the fact that, although you [Aristotelians] even label ethics as a philosophical discipline, you do not acknowledge that the divine mathematical sciences also should be adorned with the name of philosophy. In fact, if we consider this name more attentively we will clearly see that it is in itself more suited to the mathematician than to anyone else, since none of the others is more certain in his affirmations than the mathematician. And no one is more driven by the love of science in his cognition. This is evident. In fact, [the mathematician] does not rely on the senses nor accepts any presupposition that is not so true and evident to the intellect that no power whatsoever could show that it is false.4
Benedetti was acquainted with scholars quarreling over the status of mathematics, its demonstrative methods, and its legitimacy in the treatment of natural issues.
In his time such debates on the foundations and status of mathematics were intense. As an instance of epistemological reflections on the philosophy of mathematics, historians often mention the controversial theses by the Paduan
The cause of the certainty of mathematics is evident from Aristotle’sstatements. Simplicius is of the same opinion when he states (in De anima I 11) that the cause of the certainty of mathematics is due to the fact that they refer to quantity. In fact, as he argues, quantities are sensible things, they have sensible causes and they are known to us as such.6
This consideration led Piccolomini
One could argue that, just like magnitude, motion is a common sensible, too. Moreover, it has its effects and causes (see Physics V and VI). Thus, there can be a science of motion (a natural one), which is certain, similar to the science of quantity, that is, mathematics.
We can answer to this [apparent objection], that if we consider motion in general, as separated from matter and insofar as it is a continuum […], our consideration will be mathematical. This is not in contrast with our principles.7
The “ontological” and not only “epistemological” dimension of mathematical physics would concern later scholars such as Kepler
Benedetti’s interest in mathematics as a conceptual instrument accords with the interest in the demonstrative power of mathematics shown by many scholars entering the debates about mathematical certainty. The publication of Piccolomini’s
As far as the institutional side of the defence of mathematics is concerned, it opposed scholars and intellectuals benefiting from varying social status, such as mathematicians, philosophers, and theologians. Benedetti’s self-perception and, later, Galileo’s
Early polemics over the viability of the mos geometricus were not purely intellectual and academic but were also rooted in the rising recognition of the practical import of mathematics in engineering, architecture, mechanics, and warfare. A new class of intellectuals was emerging composed of “scientist-engineers,” so to speak, both expert in practical disciplines and trained in letters.10 Edgar Zilsel already remarked that the Renaissance exaltation of mathematics went far beyond purely Platonic
‘Mechanic’ is a very honored title. According to Plutarchit refers to a profession linked with warfare. It is suited to a man of high rank who is also capable of using his hands and his intelligence to realize wonderful works of rare usefulness and pleasure for human life.13
This judgment well expresses the shifting opinion on practical knowledge which also marked Benedetti’s environment. We have already stressed the centrality of practical mathematics for the Savoy
4.2 Physico-Mathematics
As a direct consequence of this mathematizing epistemology Benedetti dismissed the well-established separation between physics and mathematics in cosmology, that is, he refused to separate the investigation of “causes” and calculation.14 This anti-fictionalist perspective implied a realist commitment related to the Copernican
From this viewpoint, Benedetti’s understanding of mathematics is not too removed from that of a mathematician such as Copernicus
Benefiting from his subalpine freedom, Benedetti reflected on Pythagorean cosmology in a section entitled Pythagoreorum opinionem de sonitu corporum coelestium non fuisse ab Aristotele
As to motions, dimensions, distances, and influences there is nothing that corresponds to such proportions, but, since all of them depend upon the infinite Divine Providence of God, these velocities, those dimensions, distances, and influences must have the most perfect order and relations among them and relative to the universe.18
According to Benedetti’s outlook, the harmony of the heavens does not correspond one to one to musical harmony in the strict sense. From this viewpoint, Kepler’s
Most significantly, Benedetti and Kepler
Descartes’s
Benedetti’s place is rather at the beginning than at the end of this process. As the title of his major work hints, he was committed to a mathematical-physical investigation of nature. He did not limit his application of a mathematical method to those fields where this approach was already established, but extended it to the treatment of all realms of natural inquiry.
4.3 The Contingency of Nature and Mechanics
Benedetti’s mathematical approach to nature did not lead him to the belief that physical phenomena are ruled by necessity. Rather, he shared a medieval and early-modern ontology and epistemology of contingency enabling a particular cohabitation of mathematized physics and indeterminism (in other words, formal determination without causal necessity). In order to better understand it one has to look at Scholastic motives informing his physics, in particular his mechanics, and the scientific and philosophical work of his successors. This will require a short excursus.23
4.3.1 Scholastic Treatments of Nature as the Realm of Contingency
It would be misguided to think that a mathematical approach to nature in Renaissance science implies the assumption that natural causation is ruled by necessity. This was indeed not the case for well-established medieval and Renaissance views. Only in the course of the seventeenth century would contingency be banned from the realm of natural causation in the developments of post-Cartesian mechanism. For philosophers such as Baruch Spinoza
Historically, contingentia is the Latin variant translation of the Aristotelian
So then, the first issue has become clear: how there is contingency in things—because it comes from God—and what is in God which is the cause of this contingency—because it is his will.24
In Aristotle
This background is fundamental to understand not only theological disputes but also natural philosophical and scientific developments during the Middle Ages and the Early Modern Period. The connotation of nature as contingent—as that “which could not be”—is theological and metaphysical in its essence, since it points to the dependency of the world on God. However, from the point of view of natural conceptualizations, not only the “vertical” dimension of metaphysics is relevant but also the “horizontal” dimension of causality within nature. On the horizontal plane of the interrelation among finite beings, contingency refers to a degree of indetermination, and a certain unpredictability in the connection between causes and effects. Moreover, whereas a theological perspective focuses on the radical contingency of that which exists as created being, natural philosophy addresses the relationship between contingency and necessity within nature, that is, between divine order and phenomenal imperfection. This relationship between that which is not necessary and that which is necessary had to be conceptualized and indeed was conceptualized as the relationship between the absolutum and the conditionale or secundum quid.
In Book 1 of the Summa contra gentiles, Thomas Aquinas
The contingent differs from the necessary according to the way each of them is found in its cause. The contingent is in its cause in such a way that it can both not-be and be from it; but the necessary can only be from its cause. […] Just as from a necessary cause an effect follows with certitude, so it follows from a complete contingent cause if it be not impeded.28
A contingent cause, as one reads, will fulfill its tendency to produce a certain effect “si non impediatur,” that is, if no impediment hinders its realization.
In Book 2 of the Summa contra gentiles, Thomas
According to Scholastic terminology, there is always a “quid” producing the deviation of material phenomena from their formal rule. We will call this outlook an “ontology and epistemology of contingency.”33 The Pythagoreanism of many Renaissance scholars such as Benedetti did not depart from a view stressing the contingent character of natural phenomena in general. As we will argue, one encounters in Benedetti’s physics and mechanics a systematic use of theoretical tools implying natural contingency in the form of a distinction and interrelation between formal mathematical necessity and its material realization. In order to understand Benedetti’s mathematical treatment of contingency it is useful to consider the medieval approaches to contingency, especially the science of weights (scientia de ponderibus) he relied upon.
The idea of contingency informing physics and mechanics was related to its use in other disciplines, even ethics. Whereas there can be no obstacle impeding the realization of God’s will, which is therefore “absolute” (voluntas absoluta), human will, or voluntas secundum quid, is conditioned by circumstances. In other words, the realization of the highest aims of humankind is intrinsically contingent, as Dante
But utterance and feeling among mortals,
For reasons which are evident to you,
Have different feathers making up their wings.
I, too, as man feel this disparity […].34
Apart from ethical contingency, Scholastic authors also used secundum quid in logic. For instance, Petrus
In logic, secundum quid meant either a “diminution” of a concept through restriction of its definition (secundum quid et simpliciter), or the designation of a subject through one of its parts or characteristics (denominatio totius per partem). A secundum quid fallacy occurs if an identity is established between something considered in a particular respect and the same thing considered absolutely (or simpliciter). For instance, the existence of a depicted animal does not imply the existence of the animal simpliciter. Thus, the argument “est animal pictum, ergo est animal” is not correct. In this case, there is a quid signalizing the gap between universal necessity and particular or concrete contingency.
4.3.2 Contingent Causation in the scientia de ponderibus
The scientia de ponderibus heavily drew on the idea of the conditional limitation of natural necessity depending on circumstances (secundum situationem, also literally meant as “depending on the position”). In particular, the concept of gravitas secundum quid, or positional heaviness, had a powerful explanatory function, most notably in the Aristotelian treatment of weights by Jordanus Nemorarius
In mechanics the “limitation” or “determination” secundum quid implied that the dynamic tendency of a body was reduced or enhanced depending on intervening constraints or circumstances, in particular mechanical ones. The rotations of a lever around a pivot or of a balance around its fulcrum were conceptualized as constrained motions. In such displacements, the inherent (“necessary”) vertical tendency of a weight resulted in a circular motion due to external constraints. Similarly, the heaviness (gravitas) of the bodies suspended at the extremities of a simple machine varied in relation to their changing positions within the system. In such cases, a “necessary” straightforward motion in accordance with natural order resulted contingently in a circular one. The implicit mental model for this kind of displacement was that “circular motion is constrained rectilinear motion.” This means that, in the sublunary sphere of contingency, straightforwardness and rectilinear tendency had a higher onto-epistemological status than circularity since straightforwardness was necessarily rooted in natural order. By contrast, circularity, as the deviation from such order, had to be explained. As a consequence, circularity (in the elementary sphere) was allotted a derived and subordinated onto-epistemological status. In other words, circularity was an instance of nature departing from necessity owing to some rather elusive factor or secundum quid. From this viewpoint, it was seen as a deviant realization of given potentialities similar to moral deviation from the necessary laws of uprightness. In order to stress that the mechanical treatment of the scientia de ponderibus was embedded in the framework of contingency, we could also formulate the principle in this way: “circular motion is rectilinear motion modified by a contingency.”
Almost at the beginning of his small treatise “on the weights,” Nemorarius
[…] if equal arcs are taken on a greater circle, and on a smaller one, the chord of the arc of the greater circle is longer. From this I can then show that a weight on the arm of a balance becomes lighter, to the extent that it descends along the semicircle. For let it descend from the upper end of the semicircle, descending continuously. I then say that since the longer arc of the circle is more contrary to a straight line than is the shorter arc, the fall of the heavy body along the greater arc is more contrary to the fall which the heavy body would have along the straight line than is a fall through a shorter arc. It is therefore clear that there is more violence in the movement over the longer arc than over the shorter one; otherwise the motion would become heavier. Since something moves with more violence in the ascent [along the arc], it is apparent that there is more positional heaviness [gravitas secundum situm] and, as it is like that depending on position [secundum situationem], one can aptly call it ‘positional heaviness’ [gravitas secundum situm].37
In its circular descent along a circular path, a weight deviates from its natural tendency, or intentio, the more the arm of the balance departs from the horizontal position. Therefore, the “violence” is greater when the arc of displacement is longer, while the weight progressively loses its weight insofar as the vertical component in its motion is reduced.
According to Nemorarius
A body on one arm of the balance becomes lighter during its downward motion than an equal one located on the other extremity. Thus, as Nemorarius
Suppose now that the descent occurs on the side B and the ascent on the side C. I say that both will go back to the [horizontal] position of equality. In fact, B will not further descend, because its descent towards D is more oblique than the ascent of C towards the [horizontal position of] equality; in fact, B and C are equidistant from the place of equality.39

Fig. 4.1: Diagram accompanying preposition two in Apianus’s 1533 edition of Nemorarius’s Liber de ponderibus (1533, f. B2r). (Bayerische Staatsbibliothek)
Nemorarius’s
Fourth [proposition]: It is positionally heavier, insofar as its descent, in the same position, is less oblique.
Fifth [proposition]: But a more oblique descent partakes less of the straight [descent], for the same quantity [of the path].40
In proposition five, it is suggested that the vertical components of the potential descents of the two beams could be identified and compared. This was the source of the idea that the variation of heaviness could also be determined by comparing the straightness of the descents. A similar procedure was later taken up and explained in detail in Niccolò Tartaglia’s

Fig. 4.2: In the Quesiti et invenzioni diverse, Tartaglia argued that the relative positional heaviness of the weights A and B on a balance could be determined on the basis of the “mixed” angles of contact HAF and DBF. Since it is argued that DBF < HAF, the weight B will be heavier than A. Thus, the inclined system will strive toward the restoration of a horizontal equilibrium. (Max Planck Institute for the History of Science, Library)
In spite of his attempt to quantify the quid accounting for the alleged restorative motion of the inclined balance, Tartaglia’s
4.4 The Epistemological Import of Benedetti’s Generalization from Weights to Forces
As we have argued so far, in the medieval scientia de ponderibus circular motion is conceived of as constrained linear motion. Yet, within an Aristotelian
In the section on mechanics of the Diversae speculationes, Benedetti picked up and revised the Scholastic concept of gravitas secundum quid. Guidobaldo del Monte
Relying on the Archimedean
Benedetti shared the criticism of Nemorarius
Hence, he clearly committed himself to a mechanical theory of equilibrium based on positional heaviness. Benedetti’s technical terms are not always employed in a rigorous and consistent manner. He treats the pondus at times as the varying quantity to be taken into consideration, as is shown by expressions like “proportio ponderis in C ad idem pondus in F” and “unde fit… pondus magis aut minus grave,” in De mechanicis II (Benedetti 1585, 142). Given these semantic fluctuations, we will translate pondus as “body” or as “weight” and gravitas as “heaviness” or as “weight,” depending on the context. At the beginning of chapter 1 of his book on mechanics, Benedetti talks of a varying quantity of heaviness, or gravity (gravitas), belonging to a weight (pondus) or a body placed on a balance beam. Hence, he makes a terminological distinction between pondus, as a kind of absolute weight or heavy thing, and gravitas, as a downward tendency that can act with more or less force on the body (depending on the inclination of the beam). In this case (as in most cases in the text), pondus has the essentialist meaning of a substance (a substratum or ὑποκείμενον). It is the body or weight on the balance, whose special property of being heavy, namely the gravitas, varies depending on a quid. This quid is the position, or situm.
Benedetti seeks to quantify it by means of a method he invented. He considers the line, which he calls linea inclinationis or linea itineris, connecting a weight on an inclined balance beam to the cosmological center of gravity. Note that Benedetti calls the elementary downward tendency an iter from a merely kinematic viewpoint, but also an inclinatio from a physical and more proper one. According to him, the major or minor heaviness of the weight can be assessed through the projection of the linea inclinationis on the horizontal line passing through the fulcrum (Figure 5.1). The more distant it is from the fulcrum, the heavier the positional heaviness becomes. Thus, the weight reaches a maximum of heaviness when the balance is horizontal, and its minimum when it is vertically resting (nititur) on the fulcrum or hanging (pendet) from it. Notably, this approach anticipates the one based on the determination of the torque in classical physics, and comes to the same conclusions.45
Additionally, Benedetti equates the heaviness to a virtus, vis, or vigor, i.e., a force, which might also act in different directions (in De mechanicis, Ch. 3) and is applied to the extremity of a constrained mechanical system, like a lever or a balance. This is a significant generalization from weights to forces, but for our present discussion the most important generalization relates to rectilinear tangential tendencies in systems set in circular motion.46
The relevant treatment is the epistle to Capra
You ask me this question in your letter. Suppose a millstone rested on a virtually mathematical point and was set in circular motion, could that circular motion continue without end, assuming that the millstone is perfectly round and smooth?
I answer that this kind of motion will certainly not be perpetual and will not even last long. For apart from the fact that the wheel is constrained by the air which surrounds it and offers resistance to it, there is also resistance from the parts of the moving body itself. When these parts are in motion, they have by nature a tendency [impetus] to move along a straight path. Hence, since all the parts are joined, and any one of them is continuous with another, they suffer constraint in moving circularly and they remain joined together in such motion only under compulsion. For the more they move, the more there grows in them the natural tendency to move in a straight line, and therefore the more contrary to their nature is their circular motion. And so they come to rest naturally: for, since it is natural to them, when they are in motion, to move in straight line, it follows that, the more they rotate under compulsion, the more does one part resist the next one and, so to speak, hold back the one in front of it.47
Fig. 4.3: A diagram showing Benedetti’s considerations on the rotating millstone stressing the centrifugal tendencies of its parts. (Drawing by Irina Tupikova)
The mental model of circular motion as constrained straight motion receives in Benedetti’s treatment a higher degree of generalization. In this case, he argues that, since it contrasts with a natural inclination, it cannot be eternal. Note that this assumption (violent motion cannot be eternal) is Aristotelian
Another Aristotelian echo looms over Benedetti’s statement that the linear tendency makes a body “lighter,” since if it were freed from the constraint hindering its projection, it would not fall vertically but rather travel through a more or less rectilinear trajectory tangent to the circular motion of the constrained rotation. In the conclusion of his reflection on the natural rectilinear striving of the parts of a body set in circular motion, Benedetti stressed the originality of his treatment “without precedents” and its opposition to Aristotelian
But if you wish to see this truth more clearly, imagine that while the body, i.e., the top, is spinning around very rapidly, it is cut up or divided into many parts. You will observe not that those parts immediately fall toward the center of the universe, but that they move in a straight line, and, so to speak, horizontally. No one, so far as I know, has previously made this observation on the subject of the top.
From such motion of the top or of a body of this kind it may be clearly seen how mistaken are the Peripatetics on the subject of the forced motion of a body. They hold that the body is driven forward by the air which enters [behind it] to occupy the space left by the body. But actually the opposite effect [that is to say, resistance] is produced by the air.49
We have so far observed two instances in Benedetti’s work on mechanics in which a tension between mathematical laws of nature and their empirical realization emerges: his treatment of the rotation of a beam about its pole and that of a turning wheel. In both cases, natural straightforward tendencies are constrained and deviated into violent circular ones. The epistemological meaning of these concepts lies in the possibility of a geometrical treatment of natural contingency seen as the connection between the necessity of the rules and of the principles and their necessitation, that is, their deviation, as witnessed by the empirical reality of curvilinear motions.
4.5 From inclinatio to inertia and Beyond: Mechanistic Perspectives
René Descartes
[…] when a body is moving, even if its motion most often takes place along a curved line and, as we said above, it can never make any movement that is not in some way circular, nevertheless each of its parts individually tends always to continue moving along a straight line. And so the action of these parts, that is, the inclination they have to move, is different from their motion.51
This is the third of Descartes’s
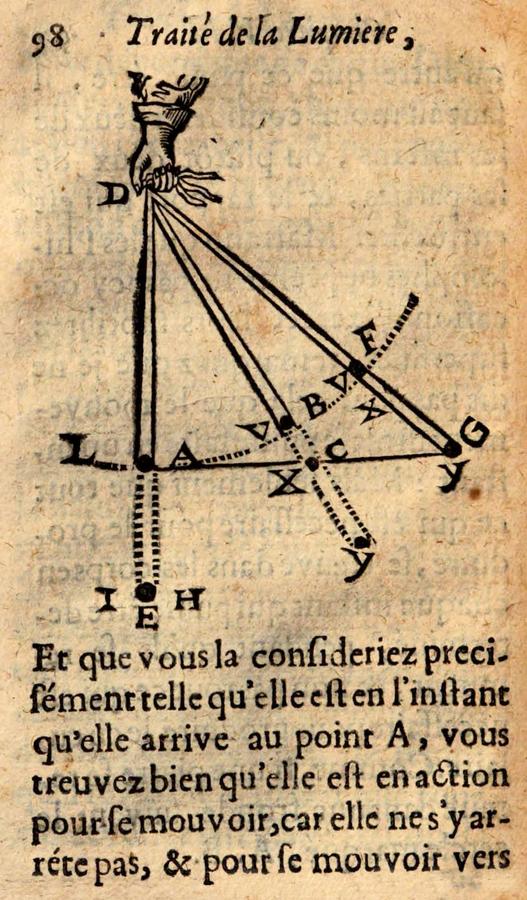
Fig. 4.4: Descartes’s visualization of the centrifugal tendency of bodies thrown by a sling, in Le Monde, Ch.7. (Bayerische Staatsbibliothek)
In the Études galiléennes, Koyré affirmed the complete independence of the law of inertia, which is only in nuce in Galileo’s
In light of our reconstruction, this statement proves quite inaccurate. As we have seen, the vertical fall of a heavy body is not the only observable straight motion: the beginning of the trajectory of a projectile thrown with great speed also looks rectilinear. Slings and catapults are in fact the instruments with which turning wheels and rotating millstones were compared, and it was from these instruments that Benedetti, Descartes
In the medieval scientia de ponderibus, two determinations were considered for the equilibrium of a balance: first, the circle resulting from the inclusion of the vertical motions of the weights in a mechanical system, and second, the situm (location) of the weights in a mechanical system determining a variation in heaviness. The reflection on gravitas secundum situm (positional heaviness) from Nemorarius
The conviction that circular motion, as a violent motion, requires an explanation is based on the mental model that “circular motion is constrained (or contingented) straight motion.” Although they were embedded in the medieval discourse on contingency, the several attempts to quantify the quid accounting for the deviation testify to the common effort to overcome the qualitative and indeterminable characterization of contingency as a form of causality. What was maintained, for instance in Descartes
The work of Benedetti and his onto-epistemology of contingency are representative of an age of transition from Scholastic and Renaissance natural philosophies to the various instantiations of the classical science of the next century. Benedetti’s Pythagorean commitment to mathematics, seen as the most powerful logical means applied to all fields of knowledge and to nature in particular, is an illustrative case of the complex and non-linear history of scientific thought. His efforts to overcome Aristotelian
Footnotes
Benedetti 1585, 298: “Miror quod cum in Aristotele sis versatus, in tuis tamen scriptis philosophum a Mathematico separes, quasi mathematicus non sit adeo philosophus, ut est naturalis, et metaphysicus, cum multo magis quam ii philosophus sit appellandus, si ad veritatem suarum conclusionum respiciamus.”
Benedetti includes a letter to Catena in Benedetti 1585, 371.
See on this De Pace 1993, 228–229.
Benedetti 1585, 298: “Verum quidem est, te in huiusmodi errore solum non versari; sed gravius est, quod cum vos videatis etiam res morales sub philosophiae appellationem cadere, non animadvertatis divinas scientias mathematicas etiam philosophiae nomine ornandas esse. Quod si eiusdem nomen penitius considerare velimus, inveniemus aperte, mathematico magis illud ipsum quam cuilibet alio convenire, cum nullus ex aliis tam certo sciat id quem affirmat quam mathematicus, neque aliquis sit, qui in cognitionis, et scientiae cupiditatem magis ducantur, ut aperte patet, cum nec etiam ipsi sensui det locum, neque aliquid praesupponat, quem non sit ita verum et intellectui notum, ut nulla quaevis potentia, illud esse falsum ostendere queat.”
Piccolomini 1565, f. 107v: “Mathematics disciplines esse certas non vi demonstrationis, sed ex subjecti ipsius ratione.”
Piccolomini 1565, 106v: “Patet igitur ex dictis Aristotelis causa certitudinis mathematicae. Hoc idem sensit Simplicius, qui primo de Anima 11. dicit causam certitudinis mathematicarum esse, quia versantur circa quantum. Quantitates enim ut dicit ipse, sunt res sensatae, et causas sensatas habent, et ideo nobis notas.”
Piccolomini 1565, 107r: “Si vero adhuc replicaretur, quod motus etiam est sensibile quoddam commune, sicut magnitudo; habet autem motus suas passionet, et suas causas, ut patet 5. et 6. Phys. ergo ita erit certa de motu scientia, naturalis scilicet, sicut scientia de quantitate, quae Mathematica est. Ad hoc respondere possumus, quod si motum consyderabimus, in communi, abstractu a materia quatenus continuum quoddam est, […] tunc consyderatio erit mathematica, et nihil contra nos.”
As Ofer Gal and Raz Chen-Morris recently stressed: “It is not epistemology that worries the two court mathematicians here, but ontology. Neither of them questions the power of mathematics to provide the knowledge they seek; it is the objects that mathematics can be true about that they both feel forced to establish.” See Gal and Chen-Morris 2013, 118–119.
The literature on the Renaissance debates on the philosophical status of mathematics is wide. Among other sources, see Giacobbe 1972, Giacobbe 1973, Carugo 1983, Jardine 1990, 693–697, De Pace 1993, Cozzoli 2007, and Axworthy 2016, chap. 2. For the Jesuit debates on mathematics, see Romano 1999. For the seventeenth century, cf. Mancosu 1996, 8–33.
See Valleriani 2010 and Valleriani 2013.
See Lefèvre 1978.
Pigafetta in Del Monte 1581: “Mechanico è vocabolo honoratissimo, dimostrante, secondo Plutarco, mestiero alla Militia pertinente, et convenevole ad huomo di alto affare, et che sappia con le sue mani et co’l senno mandare ad esecutione opre maravigliose a singulare utilità et diletto del vivere humano.”
Hypotheses on conventionalism already emerged from the debate on the conflict between Ptolemy’s geometrical models and Aristotle’s homocentric cosmology. See Di Bono 1990 and Granada and Tessicini 2005.
Most of these cosmological views are discussed in Benedetti 1585, Book 4. We deal with the details in chapter 6 as well as, partly, in chapter 7.
Bruno 2000b, doc. 13, 67: “Ho dechiarato infiniti mondi particulari simili a questo della Terra; la quale con Pittagora intendo uno astro, simile alla quale è la Luna, altri pianeti et altre stelle, le qual sono infinite.”
Benedetti 1585, 191: “Quod autem attinet ad motus, ad magnitudines, ad distantias et ad influxus, nihil est, quod hisce proportionibus conveniat, sed quia haec omnia dependent ab infinita et divina providentia Dei, necessario sit ut istae velocitates, eae magnitudines, distantiae et influxus, talem ordinem et respectum inter se ipsa et universo habeant, qualis perfectissimus sit.”
On Kepler’s discovery, see Donahue 1988, Donahue 1993 and Wilson 1968.
We have first discussed contingency and mechanics in the Renaissance in Omodeo and Renn 2015. A volume entirely devoted to ontological and epistemological contingency in the natural debates of early modernity is Omodeo and Garau 2019.
Duns Scotus 1994, 140: “Sic igitur apparet primum, quomodo est contingentia in rebus, quia a Deo, – et quid est in Deo quod est causa huius contingentiae, quia voluntas eius.”
Cf. Vogt 2011, 52. The entire first chapter is relevant for a historical overview of the reception and transformation of the Aristotelian concept of “possibility” as “contingency” in the Latin tradition.
Aquinas 1975, 221f: “Contingens a necessario differt secundum quod unumquodque in sua causa est: contingens enim sic in sua causa est ut non esse ex ea possit et esse; necessarium vero non potest ex sua causa nisi esse. […] Ex causa necessaria certitudinaliter sequitur effectus, ita ex causa contingenti completa si non impediatur.”
Thomas, Summa contra gentiles II,15. Cf. Aquinas 1975, 48: “everything that can be and not-be” and “it is indifferent to either.”
Aquinas 1975, 46: “Deus est omnibus causa essendi.”
Summa contra gentiles II 30: “In quibus [rebus] vero forma non complet totam potentiam materiae, remanet adhuc in materia potentia ad aliam formam.” Cf. Aquinas 1975, 87.
Summa contra gentiles II 23: “Omnis enim agentis per necessitatem naturae virtus determinatur ad unum effectum. Et inde est quod omnia naturalia semper eveniunt in eodem modo, nisi per impedimentum: non autem voluntaria. Divina autem virtus non ordinatur ad unum effectum tantum […]. Deus non agit per necessitate naturae, sed per voluntatem.” Cf. Aquinas 1975, 68: “For the power of every agent which acts by natural necessity is determined to one effect; that is why all natural things invariably happen in the same way, unless there be an obstacle; while voluntary things do not. God’s power, however, is not ordered to one effect only […]. Therefore, God acts, not out of natural necessity, but by His will.”
“Ma voglia e argomento ne’ mortali, per la cagion ch’a voi è manifesta, diversamente son pennuti in ali; ond’ io, che son mortal, mi sento in questa disagguaglianza […].” Also, see
Nemore 1533, f. A3v (emphasis added): “[…] si sumantur de circulo maiori et minori arcus aequales, corda arcum maioris circuli longior est. Propeterea posset ex hoc ostendi, quod pondus in libra tanto sit levius, quanto plus descendit in semicirculo. Incipiat igitur mobile descendere a summo semicirculi, et descendat continue. Dico tunc quod maior arcus circuli plus contrariatur rectae lineae quam minor, et casus gravis per arcum maiorem, plus contrariatur casui gravis, qui per rectam fieri debet, quam casus per arcum minorem. Patet ergo maior est violentiam in motus secundum arcum maiorem, quam secundum minorem. Aliter enim fieret motus magis gravis. Cum ergo plus in ascensu aliquod movetur violentiae, patet, quam maiore est gravitas secundum situm, et quia secundum situationem talium sic sit, dicatur gravitas secundum situm.”
Nemore 1533, ff. A3v–A3r: “In termino enim cuiscunque motus intenditur, intenditur et viget tota natura in actu, qui in motu sit quasi in potentia, secundum quem fiebat contrarietatis suae oppositio.”
Nemore 1533, ff. B2r–v: “Ponatur nunc, quod fiat descensus a parte B, et ascensus a parte C, dico quod redibunt ad situm aequalitatis. Non enim ulterius descendet B, eo quod descensus eius versus D magis obliquus est, quam ascensus C ad aequalitatem; B enim et C iam aequaliter distant a situ aequalitatis.”
Nemore 1533, f. A3r: “Quarta [propositio]: Secundum situm gravius esse, quanto in eodem situ minus obliquus est descensus. Quinta [propositio]: Obliquiorem autem descensum minus capere de directo, in eadem quantitate.” Translation from Renn and Damerow 2012, 63. For proposition four, see Nemore 1533, f. B3v–B4r and, for proposition five, Nemore 1533, f. B4r–C2v.
Tartaglia’s approach was controversial, already in his time. See Renn and Omodeo 2013, sec. 3.6.
Renn and Damerow 2012, 86–92. We will discuss the divergent interpretations of Benedetti and Del Monte later, in chapter 5.
Drake and Drabkin 1969, 166. Benedetti 1585, 141: “Omne pondus positum in extremitate alicuius brachii librae maiorem, aut minorem gravitatem habet.”
Renn and Damerow 2012, 138. We will deal with the details of Benedetti’s mechanics in the next section.
Cf. Büttner 2008.
Drake and Drabkin 1969, 229. Benedetti 1585, 285 (emphasis added): “Quaeris a me literis tuis, an motus circularis alicuius molae molendinariae, si super aliquod punctum, quasi mathematicum, quiesceret, posset esse perpetuus, cum aliquando esset mota, supponendo etiam eandem esse perfecte rotundam, et laevigatam. Respondeo huiusmodi motum nullo modo futurum perpetuum, nec etiam multum duraturum, quia praeterquam quem ab aere qui ei circumcirca aliquam resistentiam facit stringitur, est etiam resistentia partium illius corporis moti, quae cum motae sunt, natura, impetum habent efficiendi iter directum, unde cum simul iunctae sint, et earum una continuata cum alia. Dum circulariter moventur patiuntur violentiam, et in huiusmodi motu per vim unitae manent, quia quanto magis moventur, tanto magis in iis crescit naturalis inclinatio recta eundi, unde tanto magis contra suammet naturam volvuntur, ita ut secundum naturam quiescant, quia cum eis proprium sit, quando sunt motae, eundi recta, quanto violentius volvuntur, tanto magis una resistit alteri, et quasi retro revocat eam, quae antea reperitur habere.”
On Benedetti’s anti-Aristotelianism, see Maccagni 1983.
Drake and Drabkin 1969, 229–230. Benedetti 1585, 285: “Sed si clarius, hanc veritatem videre cupis, cogita illud corpus, trochum scilicet, dum velocissime circunducitur secari, seu dividi in multas partes, unde videbis illas omnesque, non illico versus mundi centrum descendere, sed recta orizontaliter, ut ita dicam, moveri. Id quem a nemine adhuc (quem sciam) in trocho est obseruatum. Ab huiusmodi motu trochi, aut huius generis corporis, clare perspicitur, quam errent peripatetici circa motum violentum alicuius corporis, qui existimant aerem qui subintrat ab occupandum locum a corpore relictum, ipsum corpus impellere, cum ab hoc, magis effectus contrarius nascatur.”
On the Cartesian cosmos, see Aiton 1972, 30–64 and Gaukroger 2006, 304–317.
Descartes 1998, 29. Descartes 1986, 43–44: “Lors qu’un corps se meut, encore que son mouvement se fasse plus souvent en ligne courbe, et qu’il ne s’en puisse jamais faire aucun, qui ne soit en quelque façon circulaire […], toutesfois chacune de ses parties en particulier tend toujours à continuer la sien en ligne droite. Et ainsi leur action, c’est à dire l’inclination qu’elles ont à se mouvoir, est differente de leur mouvement.”
