Chapter structure
- 5.1 An Overview of De mechanicis
- 5.2 The Beginning of Benedetti’s Mechanics
- 5.3 Del Monte’s Criticism Concerning the Non-Negligibility of the World’s Center
- 5.4 Benedetti on Weights and Forces Acting on a Balance
- 5.5 Del Monte’s Misunderstanding
- 5.6 Diverging Approaches to Tartaglia
- 5.7 The Triangulation Benedetti-Del Monte-Galileo
- Footnotes
The book on mechanics, De mechanicis, the third of the Diversae speculationes, is divided into twenty-five chapters. Mechanical issues and references to mechanics can also be found in the epistles. As to the discussion of the motion of fall through media and of hydraulic problems, these are not part of this book. De mechanicis begins with a brief preamble in which Benedetti claims that he treats topics that have never been dealt with before or have not been sufficiently explained. In this section we will discuss the positioning and controversies implicit in this strong statement in an age when mechanical studies were very lively in the Italian peninsula and abroad. We will first offer an overview of Book 3 of the Diversae speculationes. Second, we are going to look more closely at the first foundational chapters of the treatise. Third, we will consider the rivalry with Del Monte
5.1 An Overview of De mechanicis
5.1.1 The Foundations of the Theory of the Balance
Chapters 1 to 6 of De mechanicis contain a systematic account of the foundation on which Benedetti built his mechanics. Chapter 1 clarifies qualitatively how the variable weight changes depending on the obliqueness of the balance beam. While a body attached to the end of the beam has a maximum weight if the beam is in a horizontal position, it vanishes when the beam is in a vertical position. Benedetti explained this behavior as a consequence of the different extent to which the attached weight rests on the center of the balance. If the position of the beam is close to the vertical, the weight of a body attached to the end of the beam is close to zero since it rests nearly completely on the center of the balance.
Chapter 2 clarifies the positional changing of the weight quantitatively. Benedetti related the balance with an oblique position of the beam to a bent lever with one horizontal and one oblique arm, thus providing the precondition for a generalization of his result. A generalization of this kind is indeed required if the lines of inclination of the bodies at the end of a balance are conceived as being directed to the center of the earth and hence no longer as being parallel to each other. Benedetti mentioned this possibility at the end of this chapter, but considered the angle between the two directions as being too small to be measured and thus not necessary to be taken into account.
In chapter 3 Benedetti generalized from the downward inclination of a body attached to the balance beam to forces acting upon the body not vertically but making an acute or obtuse angle with the horizontal beam. Accordingly, he replaced the bodies at the end of the balance beam with two weights or two moving forces (duo pondera, aut duae virtutes moventes), as he formulated somewhat ambiguously. His derivation of their quantities was based on a reinterpretation of the horizontal distances between the center of the balance and the vertical projections of the bodies at the end of a beam in an oblique position (Figure 5.1). He interpreted these distances as perpendicular distances from the center of the balance to the lines of inclination, and was thus also able to apply the result he achieved for vertically descending weights to lines of inclination caused by forces that are not vertical.
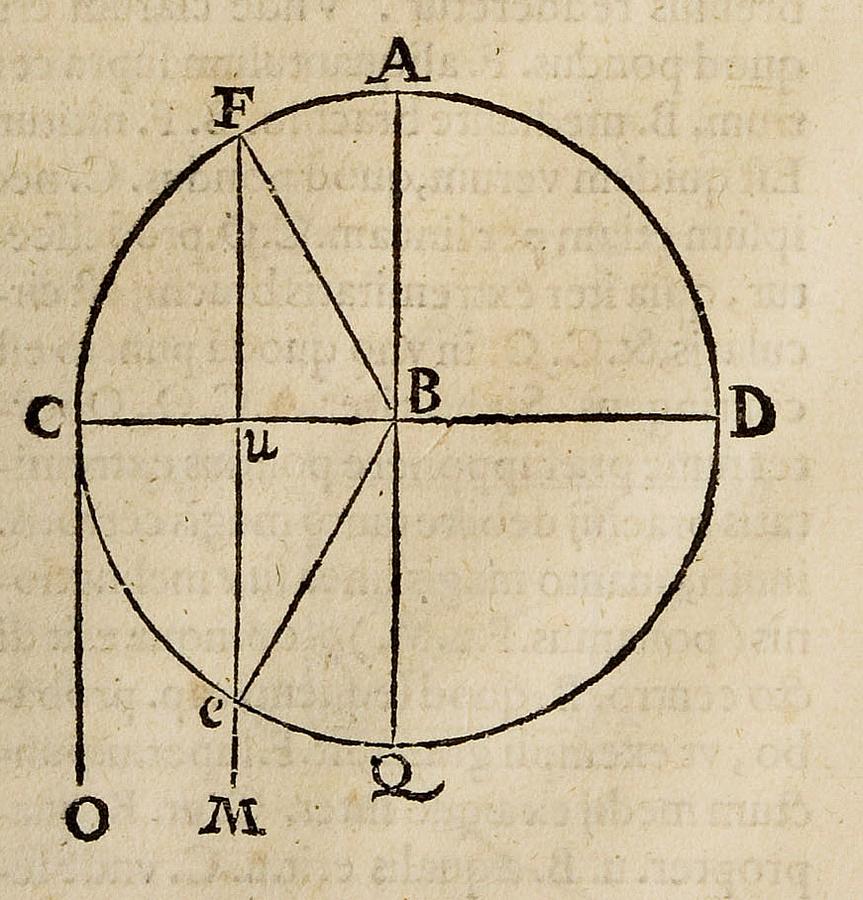
Fig. 5.1: Benedetti’s diagram showing a balance CBD or FBD. The lines CO and FUEM are the so-called lines of inclination connecting the weights C and F with the center of the elements. The length of the projection on the horizontal is proportional to the positional heaviness. (Max Planck Institute for the History of Science, Library)
Benedetti maintained that his arguments in chapters 1 to 3 clarify all the causes operating on balances and levers. To demonstrate this, he discussed in chapters 4 and 5 the validity of his results if applied to material balances and levers, taking into account that they have a beam with finite extension. This, however, does not imply that he calculated the influence of the weight of the beam itself. His discussion was rather restricted to a justification of his claim that the geometry of a rectangular beam does not require a modification of his propositions. In chapter 5 he treated the case of a lever whose fulcrum is at one of its ends.
Finally, in chapter 6, Benedetti added the description of an instrument used in bakeries for treating the dough. He explained the function of the instrument by applying his proposition from chapter 3.
The systematic approach used by Benedetti in this first part of his treatise is complemented by chapter 9, in which he explained the division of the scale of a steelyard into equal intervals.
5.1.2 Criticism of Tartaglia and Nemorarius
In chapters 7 and 8 Benedetti criticized the theorems of his former teacher Tartaglia
Chapter 7 starts with some brief critical remarks on Tartaglia’s
Benedetti’s critical remarks are somewhat eclectic. He argues that Tartaglia
Benedetti’s chapter 7 continues with a detailed discussion of the second part of Tartaglia’s
Benedetti continued in chapter 8 with critical comments on Tartaglia’s
[…] that the differences between the heaviness of these two bodies is impossible to give or find between two unequal quantities.4
Like Del Monte
Tartaglia’s
Tartaglia’s
Finally, Tartaglia’s
5.1.3 Criticism of Aristotle’s Mechanics
Benedetti’s treatise on mechanics continues mainly with critical notes on the Aristotelian
Before he embarked on this criticism, Benedetti dealt with the problem of why a steelyard carries a linear gradation in chapter 9.7 He took into account the weight of the beam and that of the scale by postulating the equilibrium of the balance when no extra weight is added. Then he added weights of one pound on both sides, arguing that, by common science (scientia communis),8 the balance stays in equilibrium if they are placed at equal distances from the fulcrum. He had thus found the mark on the beam that indicates a magnitude of one pound. He then successively placed further weights onto the scale, now arguing from the law of the lever that they must be compensated by distances proportional to their number. He thus avoided the problem of applying the law of the lever directly to a material steelyard, just as one does in practice when gauging such a balance.9
In chapters 10 and 11 Benedetti started with critical remarks on Aristotle’s
The criticism Benedetti applied to Aristotle’s
[…] whenever a body is moved in two directions in a fixed ratio it necessarily travels in a straight line.12
He concluded:
[…] if a body travels with two movements with no fixed ratio and in no fixed time, it would be impossible for it to travel in a straight line.13
For the Aristotelian author this proposition served as a means to describe circular motion as a result of two movements with no fixed ratio. Benedetti, however, did not relate his criticism to this context. He argued only that Aristotle’s
In the same vein, Benedetti’s criticism in chapter 11 then deals directly with Aristotle’s
Benedetti’s chapter 12 concerns problems 2 and 3 of the Aristotelian
If the cord supporting a balance is fixed from above, when after the beam has inclined the weight is removed, the balance returns to its original position. If, however, it is supported from below, then it does not return to its original position. Why is this?16
Aristotle
Benedetti criticized the first case by arguing that it is not only the weight of the beam that causes it to return to the horizontal position, but also the different distances of the weights in an oblique position from the vertical through the point where the beam is fixed. According to his theory of the dependency of the weight on the obliqueness of the beam, the weights must be different on both sides. Benedetti thus generalized Aristotle’s
In the second case of a beam supported from below, he argued that Aristotle
Problem 3 of the Aristotelian
In the very short chapter 13, Benedetti criticized problem 6 of the Aristotelian
Why is it that the higher the yard-arm, the faster the ship travels with the same sail and the same wind?19
The Aristotelian
[…] does not give the true explanation. For on this kind of explanation the ship would have to move more slowly rather than more swiftly. For the higher the sail that is struck by the force of the wind, the more the ship’s prow will be submerged in the water.20
Benedetti added one sentence with his own explanation, according to which the ship with a higher sail moves more swiftly because the wind blows more strongly in the higher region.
Chapter 14 provides a long discussion of problem 8 of the Aristotelian
[…] because in such a case the center will never change its position by moving upward from below, i.e., will never change its position with respect to the distance or interval which lies beween it and line AD.21
At the end of the chapter, Benedetti discussed the question of why a potter’s wheel set into motion by an external force will continue to rotate for a time but not forever. In his response he took into account the friction with the support of the wheel and with the surrounding air. But he also discussed reasons that are more deeply concerned with the nature of such motion, as we have discussed above. He claimed, in particular, that the rotational motion is not a natural motion of the wheel, evidently making reference to the Aristotelian
In chapters 15 and 16 Benedetti dealt with issues of scale as they are brought up by the Aristotelian
Why is it that we can move things raised and drawn more easily and more quickly by means of greater circles?23
In chapter 16 he discussed the tenth problem of the Aristotelian
Why is a balance moved more easily when it is without a weight than when it has one?24
In his detailed response to this problem—indeed much more detailed than the one found in the Aristotelian
In chapter 17 Benedetti addressed the twelfth problem of the Aristotelian
Why does a missile travel further from the sling than from the hand?25
Benedetti’s response is based on the concept of impetus, conceived as an intrinsic cause of motion originally acquired by the action of an external force that then gradually decreases after separation from the original mover. He argued that a greater impetus can be impressed by the sling due to the repeated revolutions which evidently lead to an accumulation of this intrinsic force. He observed that the impetus would lead, if not impeded by the sling or the hand, to a straight motion of the projectile along the tangent to the circle of its forced motion. He also noted—distancing himself from a claim made by Tartaglia
In chapter 18 Benedetti considered problem 13 of the Aristotelian
In chapter 19 he handled problem 14 of the Aristotelian
Why is a piece of wood of equal size more easily broken over the knee, if one holds it at equal distance far away from the knee to break it, than if one holds it by the knee and quite close to it?28
Again, Benedetti just referred to the earlier chapters of his treatise.
In chapter 20 Benedetti reconsidered problem 17 of the Aristotelian
Why are great weights and bodies of considerable size split by a small wedge, and why does it exert great pressure?29
In the Aristotelian text, the answer is based on interpreting the wedge as two levers opposite to each other, their fulcra being placed at the entry points of the wedge into the wood. Benedetti, however, disagreed with the identification of the two levers allowing the action of the wedge to be interpreted in terms of force, fulcrum, and resistance. He claimed that the fulcrum is actually placed just underneath the deepest point of the opening produced by the wedge entering a block of wood.
In chapter 21 Benedetti claimed to provide the true explanation of compound pulleys. He reduced a compound pulley to a chain of balances by appropriately identifying forces and fulcra, each wheel of the pulley corresponding to one balance.
In chapter 22 Benedetti discussed Aristotle’s
A difficulty arises as to how it is that a greater circle, when it revolves, traces out a path of the same length as a smaller circle, if the two are concentric.30
While the author of the Mechanical Problems referred to dynamical reasons in explaining this apparent paradox, Benedetti resorted to a kinematic argument, a pointwise reconstruction of the trajectory of the motion of a point on the circumference, arguing that it results from a superposition of two motions. In the case in which the motion is controlled by the larger circle, a point on the circumference of the smaller circle traverses a path resulting from an addition of two motions. In the case in which the motion is controlled by the smaller circle, a point on the circumference of the larger circle traverses a path resulting from a subtraction of two motions.
Chapter 23 of Benedetti’s treatise does not exist.31 In chapter 24 Benedetti discussed problem 30 of the Aristotelian
Why is it that when men stand up, they rise by making an acute angle between the lower leg and the thigh, and between the trunk and the thigh?32
In his response Benedetti suggested that the reason for this behavior is to create an equilibrium of the body with regard to the line that serves as support underfoot.
In chapter 25 Benedetti addressed the last problem, problem 35 of the Aristotelian
Why do objects which are travelling in eddying water all finish their movement in the middle?33
Benedetti’s answer simply referred to the fact that whirlpools are depressed in their middle without giving an explanation of this phenomenon. He could thus restrict himself to arguing that the motion of an object to the center of such a whirlpool is simply its natural downward motion. The final comment by Benedetti is a remarkable conclusion to his criticism of Aristotle
But in the case of all those other problems that I have omitted, Aristotle’sexplanations are correct.34
5.2 The Beginning of Benedetti’s Mechanics
After our overview of Benedetti’s book on mechanics, we concentrate on the theses he expounded in the first chapters because they have a foundational character and proved particularly controversial, at least in light of Del Monte’s
5.2.1 De mechanicis I: “On the different positions of balance beams”
In chapter 1, Benedetti notes that “a body (pondus) […] acquires a larger or smaller weight (gravitas) depending on the different ratio of the beam’s position” (pondus… maiorem, aut minorem gravitatem habet, pro diversa ratione situs ipsius brachii). According to him, a body has the greatest heaviness when the beam at whose extremity it is loaded is in the horizontal position. His idea is based on a simple common-sense intuition: if one considers an equal-arms balance suspended at its center, the weight of a loaded body is:
borne entirely by the fulcrum when resting vertically upon it,
entirely hanging on the fulcrum when suspended vertically below it,
not supported in any way by the fulcrum when the beam is in the horizontal position.
In the first case, the body completely rests or leans on the center (nititur), and the center in turn hinders (impellet) the downward tendency of the weight. In the second case, the body is suspended vertically (pendet) and the center “attracts” it (attrahet), in the sense that it hinders its natural tendency to fall down (inclinatio). Hence, the body attains its maximum weight in the third case. If the balance beam moves upward, departing from the horizontal position, the weight slowly decreases and reaches its minimum at the top when the beam is in the vertical position. If the rotatory motion around the fulcrum continues, now downward, the weight increases again until it reaches its maximum in the horizontal position. It then diminishes until it is suspended entirely below the fulcrum. Benedetti visualizes these variations of weight depending on the position (situs) in a diagram comparing the lines connecting the weight to the center of the world in different cases, more specifically if the beam is:
horizontal,
raised upward, or
moved downward with the same angle as in the second case (which is equivalent to 2).
The parallel lines, called lineae inclinationis or lineae itineris, indicate the direction in which a body would fall if it were free. The closer these lines are to the center of the beam, Benedetti says, the “less heavy” the body becomes.
In his own copy of Benedetti’s book, Del Monte
5.2.2 De mechanicis II: On the proportion of weights at the extremities of a balance beam in a position other than the horizontal
In chapter 2, Benedetti deals with the proportions of a weight placed at the extremity of a balance beam if its position is not horizontal (De proportione ponderis extremitatis brachii librae in diverso situ ab orizontalis). The thesis to be demonstrated is the following: “The proportion between [the weight of] a body (pondus) at C and [the weight of] the same body (pondus) at F corresponds to that between the whole beam BC and its part BU, which is [set on the beam BC and is] delimitated by the fulcrum and the [intersection between the beam and the] inclination line FUM that connects the weight at F to the center of the world” (Benedetti 1585, 142). For the sake of simplicity, we will represent these relations symbolically in modern terms:
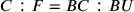
|
where C is the weight in the horizontal position and F in the inclined position; BC is the beam and BU the part of the beam BC between the center B and the perpendicular line drawn from F.
Benedetti’s demonstration is as follows. He imagines placing a weight D on the other extremity of the balance that has the same proportion to C as F, that is, the following proportion expressed in modern terms:
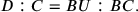
|
In accordance with Archimedes’s
The next step is to show that F : C = BF : BU (where BF is the beam, hence BF = BC). In order to demonstrate this, Benedetti resorts to the mental model (imaginemur) of a string hanging vertically from F, to which a weight equal to C is suspended. He claims that it is visually evident that the weight has the same effect at F as at U. The same is valid for the case in which the weight is suspended from U and intersects the circumference described by the rotation of the beam at a point E. In both cases, the balance would remain horizontal since the weight C at F, U, or E would balance the weight at D. Benedetti further argues that the balance under consideration can be treated like a bent lever with a horizontal and an inclined arm (FBD or EBD): “si brachium BE consolidatum fuisset […]” (If the beam BE was made solid […]).
The author concluded that his reasoning has satisfactorily demonstrated his thesis: “A body (pondus) is more or less heavy (grave) the more or less it hangs from (pendet) or rests on (nititur) the fulcrum” (Benedetti 1585, 142). And he deems this resting on or hanging from the fulcrum to be the most direct cause (haec est causa proxima, et per se) of the positional changing of a weight.
As an additional commentary, Benedetti remarks that in his diagram he supposes the inclination line CO to be perpendicular to CB and parallel to BQ, whereas CO and BQ in fact converge at the center of the sphere of the elements (centrum regionis elementaris), that is, the earth. But for the sake of his present argumentation, this angle is negligible and one may simply assume perpendicularity and parallelism. Benedetti thus developed a method to quantify positional heaviness that corresponds to the modern concept of “torque.”
5.3 Del Monte’s Criticism Concerning the Non-Negligibility of the World’s Center
As will be shown in the following section, it was only in his initial treatment of the inclined balance, in chapter 1 of De mechanicis, that Benedetti neglected to consider the convergence of the inclination lines to the center of the elements. This omission gave rise to criticism. Del Monte
In a marginal note to the Diversae speculationes (Figure 5.2), Del Monte
because that [that is, the greater or smaller extent to which a weight rests at the center] is neither the next [cause] nor the [cause] in itself. For the weight at F of the arm BF is not equally heavy as the weight U of the arm BU; nor is the weight at E of the arm BE equally heavy as the weight at U of the arm BU. Thus, this entire demonstration is false.37

Fig. 5.2: Del Monte’s marginal note to De mechanicis, II. (Max Planck Institute for the History of Science, Library)
This means that Del Monte
To find Del Monte’s
In his diagram (Figure 5.3) Del Monte

Fig. 5.3: Del Monte’s critical reworking of Benedetti’s diagram in Meditatiunculae, f. 145. (Bibliothèque Nationale de France)
Next, he considered a bent lever made of the oblique arm BS, rigidly connected to the straight arm BD, assuming that BU is half BD. If a weight is now placed at S that is double the weight at D, the bent lever will be in equilibrium, as Del Monte
He proceeded to demonstrate this in greater detail by considering the proportions into which the line connecting the two weights is cut by the perpendicular BQ for the two cases, that is, the weight placed at S and the weight placed at E. Del Monte
Del Monte
5.4 Benedetti on Weights and Forces Acting on a Balance
Chapter 3 of Benedetti’s De Mechanicis contains a generalization of the results of chapter 2 or, rather, presents a general rule concerning the action of forces (virtutes) on balance beams, including in the case that they do not act vertically downward but also with an acute or obtuse angle. Benedetti moves forward from the result of the previous chapter as follows: the length of the line perpendicularly connecting the center to the line of inclination (the line BU in the diagram) allows the quantity of the positional force (quantitas virtutis… in… situ) of a weight (F in the diagram) to be established. Thus, Benedetti calls the positional weight a force, and this is the presupposition that allows him to generalize from gravitas the action which he calls virtutes moventes, or “moving forces.” The thesis of this chapter is summarized in its title: “That the quantity of any given weight (pondus) or moving force in relation to another quantity can be determined thanks to the perpendicular projections connecting the center of the balance to the line of inclination.”
Benedetti draws two diagrams showing a balance at whose extremities two weights or forces act in different directions (Figure 5.4). At the left extremity B, a weight E has a downward tendency, while at the right extremity, a weight C acts making an acute or an obtuse angle. According to Benedetti, the length of the perpendicular projection drawn from the center to the inclination line, OT, permits the determination of the distance OI on the beam at which the same force acting vertically downward produces the same effect. Given this equation, Benedetti can determine how much the force acting in a non-perpendicular direction has to be augmented in order to balance an equal weight acting perpendicularly on the opposite beam. This measure is given according to the following proportion (expressed in modern terms):

|
where E is the weight acting vertically on the extremity B; C is the virtus movens acting on the opposite extremity A at an angle; BO is the left beam and OI the part of the right beam OA determined as explained above.
In his argumentation, Benedetti thus equates a balance (BOI) with a bent lever (BOT). Accepting this equation, he concluded that, according to commonly shared knowledge (communi quadam scientia), the weights or forces that are required to obtain a perfect balance can easily be calculated.
The chapter ends with a cosmological corollary: “The closer the center O of the balance is to the center of the elementary sphere, the less heavy (minus grave) it becomes.” In fact, the angles between the beam and the inclination lines become progressively smaller.
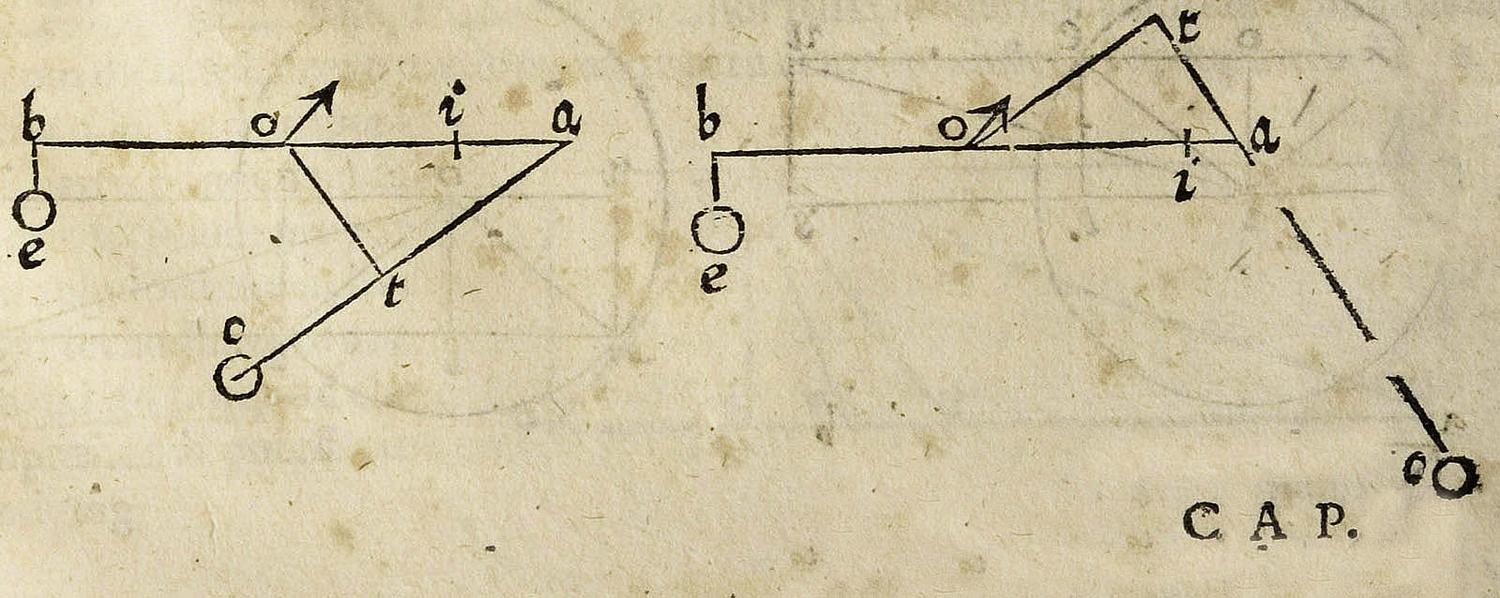
Fig. 5.4: Benedetti’s representation of forces acting on a balance in arbitrary directions. (Max Planck Institute for the History of Science, Library)
5.5 Del Monte’s Misunderstanding
In his notes on folio 146 of the Meditatiunculae, Del Monte
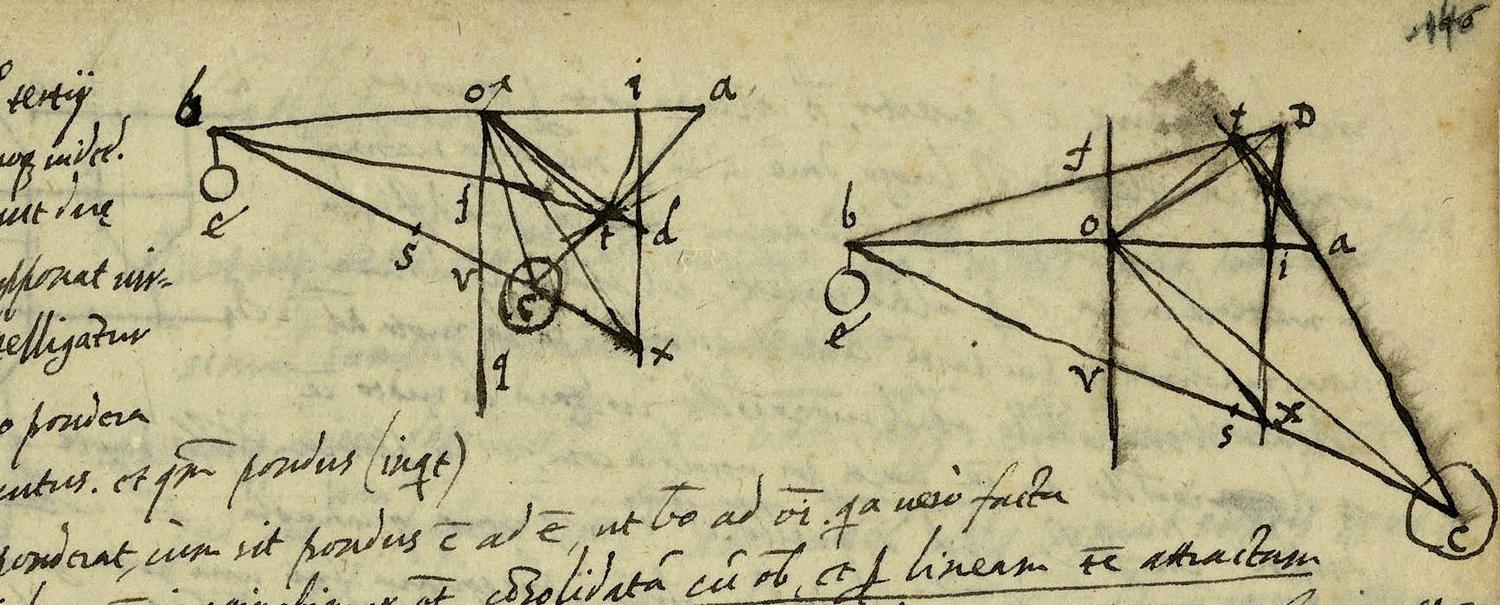
Fig. 5.5: Del Monte’s critical reworking of Benedetti’s representation of forces acting on a balance in arbitrary directions. (Bibliothèque Nationale de France)
He first recapitulated Benedetti’s procedure, assuming that a vertical line OT drawn from the fulcrum to the line AC represented the oblique arm of the bent lever. He stated that when the weight C is placed at the end of the horizontal line OI, whose length is the same as that of the perpendicular OT, according to Benedetti it will be in equilibrium with the weight E if the weight C is to the weight E as is BO to OT or OI. Del Monte
Del Monte
Del Monte
Using the same pattern, he continued by showing that the bent lever BOC cannot be in equilibrium because its center of gravity S can never fall on the perpendicular line OU through the fulcrum. Finally, he applied this argument to the broken bent lever BOTC. Del Monte
As an afterthought, Del Monte
The following considerations enable Del Monte’s
If we understand that a weight is at C, as we can assume from his own words, then CT must also be understood as being solid [and connected with] the solid lines TO […] If we hence understand that C is a weight and not moving, [the proposition] is false. If it is understood that C moves as […] of a man, it can be true, since what moves is not a weight. [But] if he himself assumes in the following that [this] can be demonstrated [also for a weight], nothing […] therefore as is evident in chapter 7. All demonstrations of the author are founded on these two chapters inasmuch as they are the first fundaments of mechanics; once their falsity is recognized, everything is rejected.38
5.6 Diverging Approaches to Tartaglia
Del Monte’s
5.6.1 The Tradition of Nemorarius, Tartaglia, and Cardano
The concept of gravitas secundum situm, or positional heaviness, was extensively employed in Jordanus Nemorarius’s
In the sixteenth century, Tartaglia
Descent: A first method of dealing with positional heaviness consisted in comparing the lengths of the projections of the equal arcs described by the motion of opposite balance beams—one ascending and one descending—on the vertical line of descent to the center of the world.
As Tartaglia’s
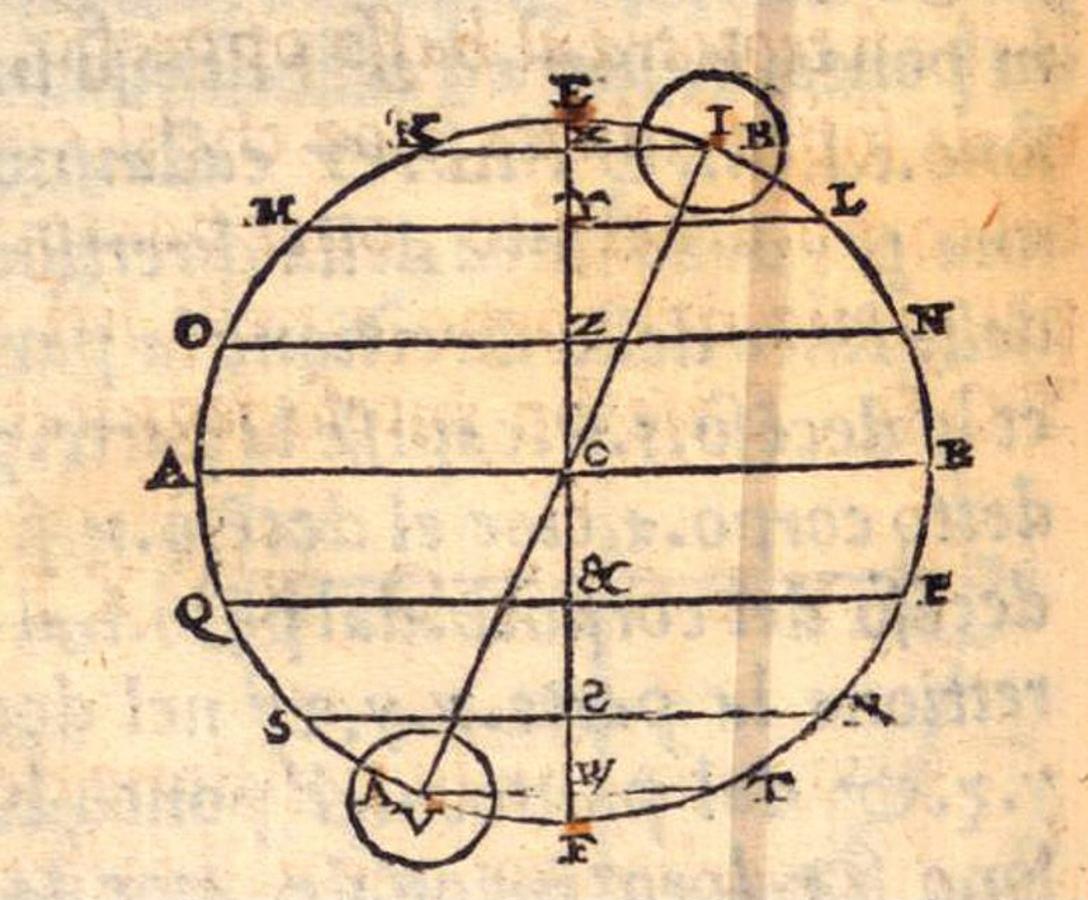
Fig. 5.6: According to Tartaglia, the body at I is positionally heavier than the body at V, since the projection of the arc IL on the vertical XY is greater than the projection of VF, WF. (Max Planck Institute for the History of Science, Library)
Angle of contact: Tartaglia’s
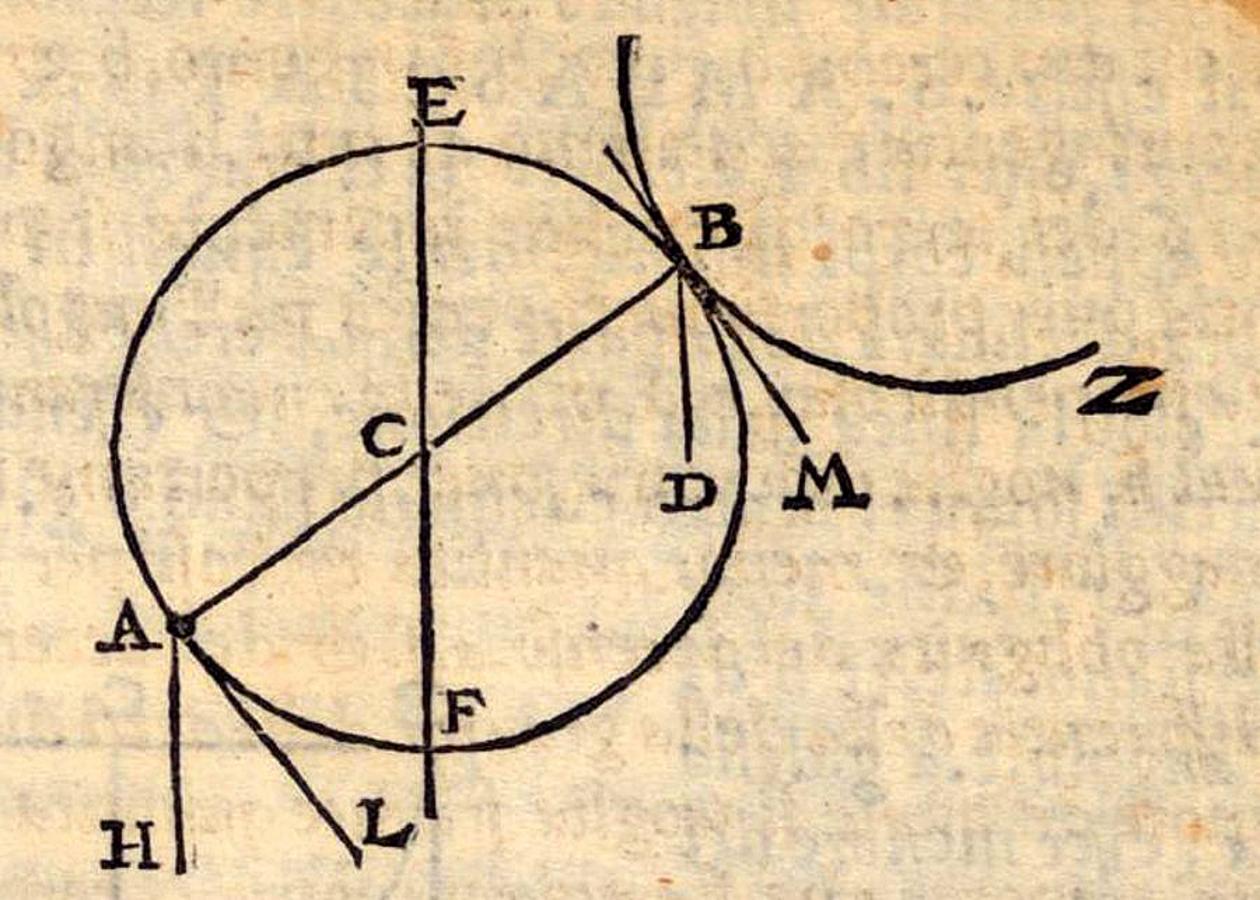
Fig. 5.7: Tartaglia’s representation of the angle of contact for the determination of positional heaviness. (Max Planck Institute for the History of Science, Library)
By comparing the angles of contact of the two weights, Tartaglia
The angle between the support and the beams: We have so far considered two ways of determining positional heaviness on the basis of Tartaglia’s
Aristotlesays that this happens when the support is above the balance, because the angle QBF of the meta is larger than the angle QBR. And similarly, when the support is QB, the meta will be AB, and thus the RBA will be larger than the angle FBA, but the larger angle will render the weight heavier. […] The general reason is hence this: the more the weights are removed from the meta or from the line of descent along a straight or an oblique line, that is, [as measured] by an angle, the heavier they are.39
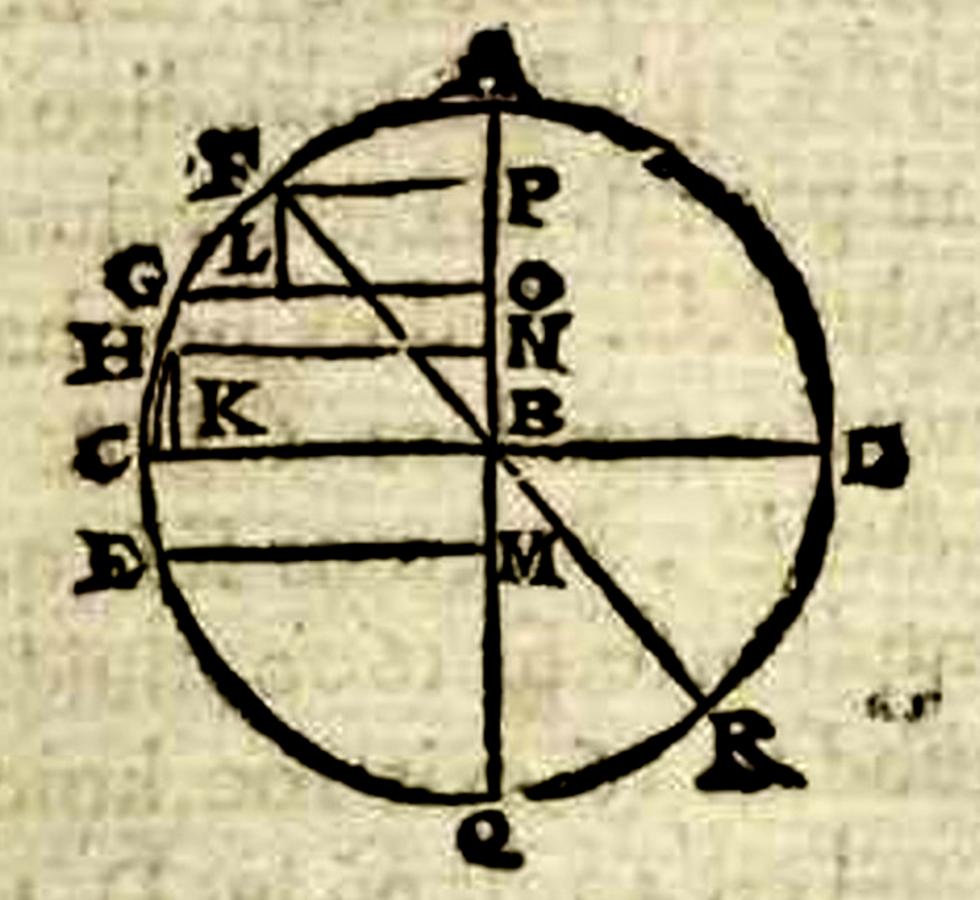
Fig. 5.8: According to Cardano, there are three ways to determine positional heaviness. The positional heaviness at point F, for instance, may be determined by the horizontal FP, by the vertical FL, or by the angle QBF. (Max Planck Institute for the History of Science, Library)
Given these premises, Cardano
5.6.2 Del Monte’s Critical Remarks on Positional Heaviness
Del Monte’s
The center of gravity is a certain point within it, from which, if it is imagined to be suspended and carried, it remains stable and maintains the position which it had at the beginning, and is not set to rotation by that motion.40
Apart from the conceptual irreconcilability between his own approach and that of the Nemorarius
Contrary to the assumptions of Nemorarius
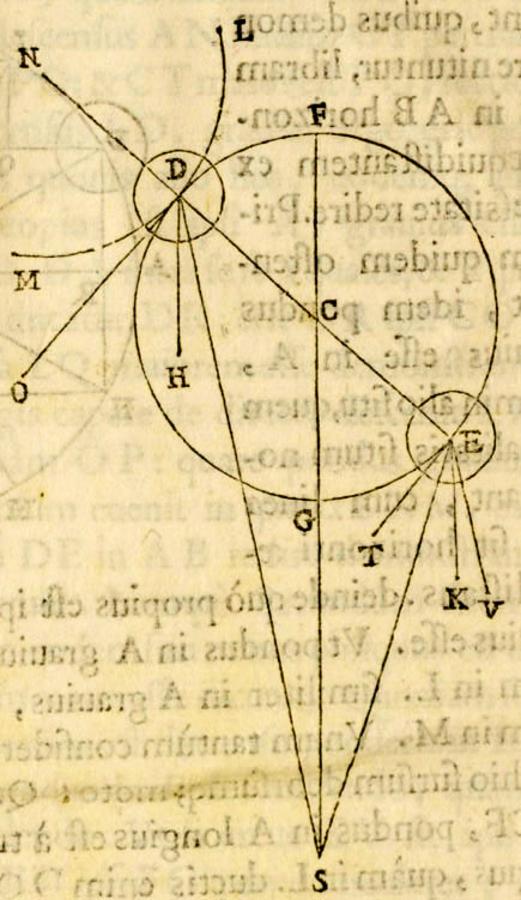
Fig. 5.9: According to Del Monte, if S represents the center of the world, then the mixed angle SEG between the circular path of the weight at E and the direction to the center of the world is less than the mixed angle SDG. Thus, contrary to what his adversaries claim, by their own suppositions the weight placed at E must be heavier than that at D. (Max Planck Institute for the History of Science, Library)
Del Monte
Del Monte’s
5.6.3 Benedetti on Tartaglia’s and Nemorarius’s Shortcomings
Benedetti addressed the ideas of Tartaglia
More specifically, Benedetti refuted several of Tartaglia’s
Nevertheless, Benedetti did not believe in an indifferent equilibrium of such a balance when considered in a cosmological context. In the continuation of his argument, he came to the conclusion that when such a balance in equilibrium is displaced from its original horizontal position, the weight that has been lowered will actually assume a greater positional heaviness than the one that has been lifted up:
Therefore the weight of A in this [lower] position will be heavier than the weight of B.41
He reached this conclusion by taking into account that the lines of inclination of the two weights are not parallel to each other but must converge at the center of the elements. The effective lever arms of the two weights must hence be determined by perpendicular lines drawn from the center of the balance to these lines of inclination. It now turned out that the perpendicular line corresponding to the weight that had been lowered is longer than the line corresponding to the weight that had been lifted. Consequently, the lower weight had become heavier positionally, so that one would expect the balance to tilt into a vertical position.
Benedetti added some more critical remarks on Tartaglia’s
Now the whole error into which Tartagliaand Jordanus fell arose from the fact that they took the lines of inclination as being parallel to each other.42
In summary, Benedetti introduced a way of determining the positional effect of a weight or a force that, in the cases he considered, essentially produces the same results as the application of the modern concept of torque. In particular, Benedetti had managed to go beyond the consideration of weights tending downward to include forces acting in an arbitrary direction. In this way, he was also able to take into account the fact that, on a spherical earth, the lines of inclination of weights on a balance are not parallel. He did not manage, however, to successfully apply his measure of positional heaviness to challenging objects such as the inclined plane.
5.7 The Triangulation Benedetti-Del Monte-Galileo
In this chapter, we have dealt with Del Monte’s
In conclusion, it may be useful to recall the problems linked to the triangulation Benedetti-Del Monte
An important clue is page 145bis of the Meditatiunculae (Figure 5.10), which is the page opposite the one containing the detailed criticism of Benedetti dealt with in this chapter. This page shows Galileo’s
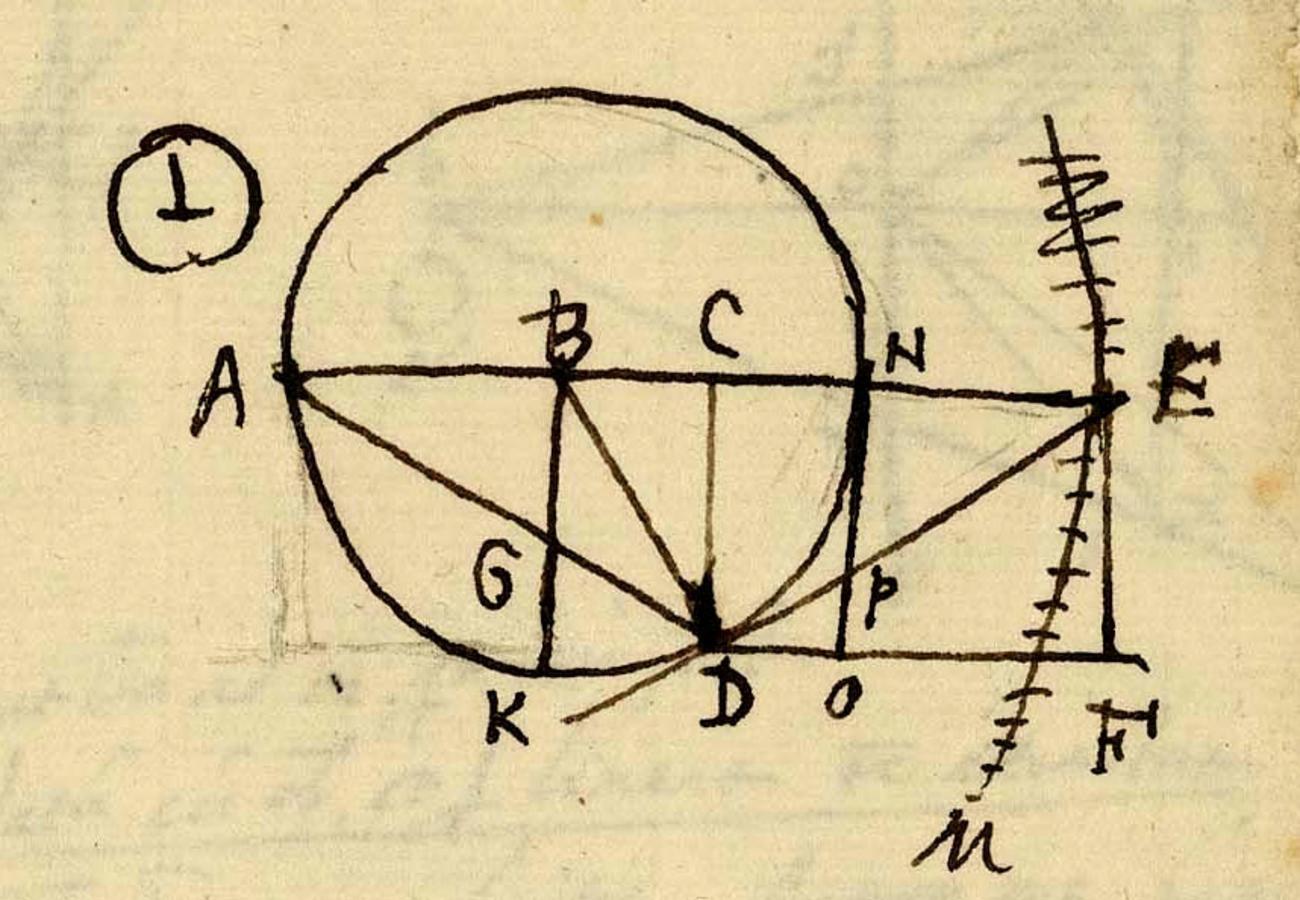
Fig. 5.10: Del Monte, Meditatiunculae, p. 145bis showing Galileo’s construction relating the bent lever to the inclined plane. (Bibliothèque Nationale de France)
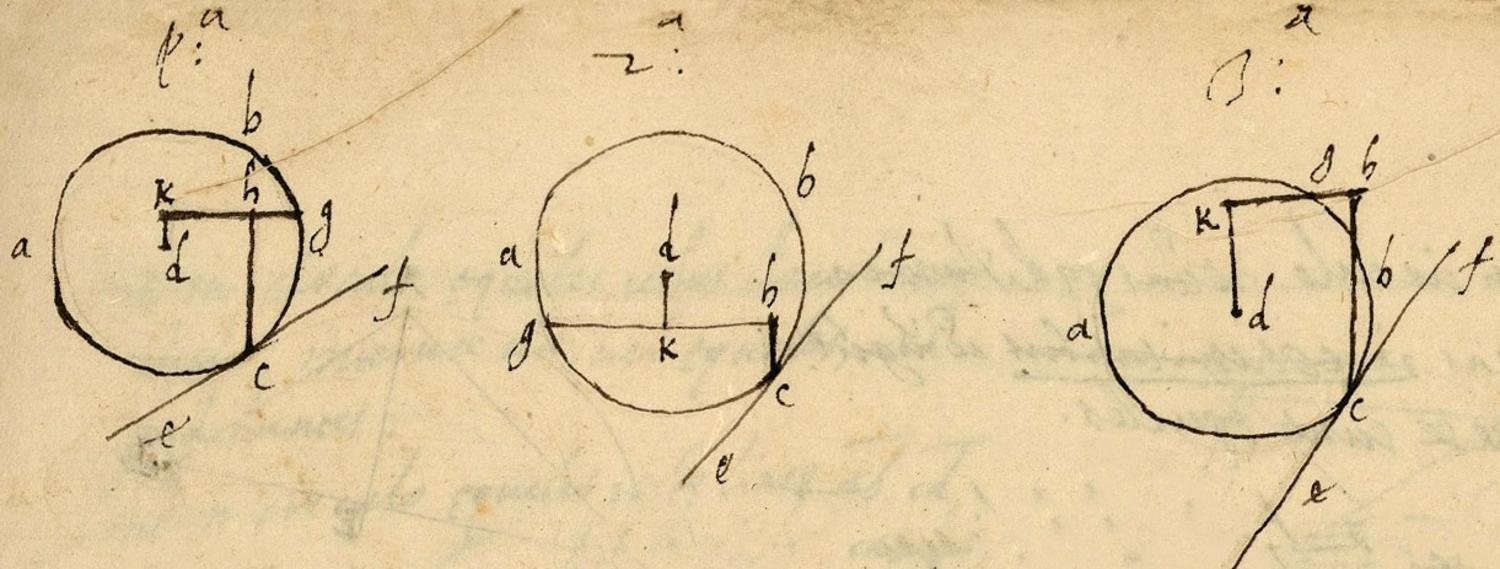
Fig. 5.11: Del Monte’s construction related to the inclined plane on p. 64 of his notebook. The construction was adapted from Pappus’s erroneous solution. (Bibliothèque Nationale de France)
This fact is all the more noteworthy since Del Monte’s
Recent research into Del Monte’s
In particular, Galileo’s
Center of gravity is defined as that point in every heavy body around which parts of equal moments are arranged.53
The evidence for this claim concerning Benedetti’s legacy in Galileo’s
According to Benedetti and Galileo
There is one thing that must be considered before proceeding further, and this concerns the distances at which heavy bodies come to be weighed; for it is very important to know the sense in which equal and unequal distances are to be understood, and in what manner they must be measured.55
In his analysis of the inclined plane using the bent lever, Galileo
In conclusion, the very existence of Del Monte’s
Footnotes
Section 5.1 is derived from Renn and Damerow 2012, chap. 6.1–6.3 and section 5.2 from Renn and Omodeo 2013.
Tartaglia 1546, 91r: “[…] che la differenzia ch’è fra le gravità de questi dui corpi egli è impossibile a poterla dar, over trovar’ fra due quantità inequali.” Translation in Drake and Drabkin 1969, 130.
We will discuss Benedetti’s criticism in more detail later.
Aristotle 1980. See Rose and Drake 1971 and also the introduction to Nenci 2011.
In the sixteenth century the term scientia communis was used to designate knowledge common to all mathematical sciences, its core being the Euclidean theory of proportions. See Sepper 1996, 153–154.
See the discussion in Damerow et al. 2002.
Aristotle 1585, 507: “Quandoquidem igitur in proportione fertur aliqua id, quod fertur, super rectam ferri necesse.” Translation in Aristotle 1980, 1, 848 b 11–848 b 13 (337).
Aristotle 1585, 508: “Si autem in nulla fertur proportione secundum duas lationes nullo in tempore, rectam esse lationem est impossibile.” Translation in Aristotle 1980, 339.
Aristotle 1585, 511: “Cur siquidem sursum fuerit spartum, quando deorsum lato pondere, quispiam id admovet, rursum ascendit libra: si autem deorsum constitutum fuerit, non ascendit, sed manet?” Translation in Aristotle 1980, 347–349.
Aristotle 1585, 515: “Cur quando antenna sublimior fuerit, iisdem velis, et vento eodem celerius feruntur navigia?” Translation in Aristotle 1980, 361.
Benedetti 1585, 155: “[…] verum non est. Huiusmodi enim ratione navis tardius potius, quam velocius ferri deberet, quia quanto altius est velum, vi venti impulsum, tanto magis proram ipsius navis in aquam demergit.” Translation in Drake and Drabkin 1969, 183.
Benedetti 1585, 155: “[…] quia huiusmodi centrum ab inferiori parte ad superiorem, nunquam mutabit situm respectu distantiae seu intervalli, quae inter ipsum lineamque AD intercedit.” Translation in Drake and Drabkin 1969, 184.
For the historical context, see Büttner 2008.
Aristotle 1585, 517: “Cur ea, quae per maiores circulos tolluntur et trahuntur, facilius et citius moveri contingit […]?” Translation in Aristotle 1980, 365.
Aristotle 1585, 517: “Cur facilius quando sine pondere est, movetur libra, quam cum pondus habet?” Translation in Aristotle 1980, 365.
Aristotle 1585, 518: “Cur longius feruntur missilia funda, quam manu missa […]?” Translation in Aristotle 1980, 367.
See the discussion in Renn, Damerow, and Rieger 2001.
Aristotle 1585, 518: “Cur eiusdem magnitudinis lignum facilius genus frangitur, si quispiam aequi diductis manibus extrema comprehendens fregerit, quam si iuxta genu?” Translation in Aristotle 1980, 369.
Aristotle 1585, 520: “Cur a parvo existente cuneo magna scinduntur pondera, et corporum moles, validaque sit impressio?” Translation in Aristotle 1980, 371.
Aristotle 1585, 525: “Dubitatur quam ob causam maior circulus aequalem minori circulo convolvitur lineam, quando circa idem centrum fuerint positi.” Translation in Aristotle 1980, 387.
In Drake and Drabkin 1969, 193; chapter 22 is erroneously numbered as chapter 23.
Aristotle 1585, 532: “Cur surgentes omnes, femori crus ad acutum constituentes angulum, et thoraci similiter femur, surgunt?” Translation in Aristotle 1980, 403–405.
Aristotle 1585, 533: “Cur ea quae in vorticosis feruntur aquis, ad medium tandem aguntur omnia?” Translation in Aristotle 1980, 409.
Benedetti 1585, 167: “[…] a quo aliarum omnium quaestionum, quas ego omisi rationes sunt bene propositae.” Translation in Drake and Drabkin 1969, 196.
“Hoc primum caput to[tum] desumptum est a n[ostro] Mechanicorum libri tractatu de lib[ra].”
“[…] unde fit ut hoc modo pondus magis aut minus a centro pendet aut eidem nititur: atque haec est cause proxima, et per se […].”
See Renn and Damerow 2012, 207: “non est neque proxima neque per se; nam [pond]us in F brachii [BF] non est equegrave ut pondus in U brachii BU; [nec] pondus in E brachii BE est equegrave ut pondus [in] U brachii BU. Unde tota haec demonstratio falsa est.”
See Renn and Damerow 2012, 213: “si intelligamus p[ondus] in C, ut supponi p[otest] ex verbis ipsius, intelligendum est C[T] quoque consolidatam consolidatis TO […]. Unde si intelligamus C pondus et non movens, falsa est i[ta]que si intelligatur C movens ut homi[…] vera esse pote[st] quod [deleted: non] moveat non esse pondus s[i…] ipse [vero] in sequenti accipiat [hoc atque ponderi?] posse demonstratum quare nihil […] ut patet in 7 cap. In his duobus cap. fundantur omnes authoris demonstrationes ita ut sunt praecipua mechanicorum fundamenta quorum cognita falsitate omnia rem[oventur].”
Cardano 1550, 17–18: “Aristoteles dicit hoc contingere, quum trutina est supra libram, quia angulus QBF metae, maior est angulo QBR. Et similiter quum trutina fuerit QB, erit meta AB, et tunc angulus RBA, maior erit angulo FBA, sed maior angulus reddit gravius pondus. […] Generalis igitur ratio haec sit: pondera quo plus distant a meta seu linea descensus per rectam aut obliquum, id est, per angulum, eo sunt graviora.”
Del Monte 1577, 1r: “Centrum gravitatis uniuscuiusque corporis est punctum quoddam intra positum, a quo si grave appensum mente concipiatur, dum fertur, quiescit; et servat eam, quam in principio habebat positionem: neque in ipsa latione circumvertitur.” Translation in Drake and Drabkin 1969, 259, revised in Damerow and Renn 2010, 57.
Benedetti 1585, 148: “Pondus igitur ipsius A in huiusmodi situ, pondere ipsius B gravius erit.” Translation in Drake and Drabkin 1969, 176.
Benedetti 1585, 150: “Omnis autem error in quem Tartalea, Iordanusque lapsi fuerunt ab eo, quod lineas inclinationum pro parallelis vicissim sumpserunt, emanuit.” Translation in Drake and Drabkin 1969, 177.
See the discussion by Ventrice in Bordiga 1985, 732–736. He mentions Drake, Drabkin, Fredette, and Galluzzi among those who are skeptical about a concrete influence of Benedetti on Galileo. Notable exceptions are the commentaries by Carugo and Geymonat in their edition of Galileo’s Discorsi, see Carugo and Geymonat 1958. Bertoloni Meli even considers the possibility of Del Monte and Galileo discussing Benedetti, but nevertheless rejects any substantial influence by the latter on Galileo’s thinking because that influence supposedly would have arrived too late, see Bertoloni Meli 2006, 61–65.
Cozzi and Sosio 1996. For an overview of such potential connections, see the discussion in Bordiga 1985, 732–736 who also mentions Mersenne, Clavius, and Cardinal Michelangelo Ricci as possible intermediaries.
For an overview, see Bordiga 1985.
See, for instance, Drake and Drabkin 1969, 36. Yet, the question of Benedetti’s direct impact on Galileo remains unclear, in particular as Benedetti’s work was never mentioned by Galileo.
There are several possible connections between Benedetti and Galileo that have been considered in the past. For instance, Benedetti is referred to by Galileo’s Pisan colleague Jacopo Mazzoni in In universam Platonis et Aristotelis philosophiam praeludia from 1597. See Mazzoni 1597. He is often mentioned in the Galileo Studies as the addressee of a famous letter by Galileo arguing for the Copernican system (May 30, 1597) . See Galilei 1968, vol. 2, 194–202 . In his book Mazzoni referred to Benedetti’s discussion of the possibility that motion along a straight line can be continuous. See Benedetti 1585, 183–184. For a historical discussion of the context of this argument in contemporary technology, see Freudenthal 2005, a theme that was later taken up by Galileo in chapter 20 of De Motu, which also refers explicitly to Copernicus. See Mazzoni 1597, 193 and Galilei 1960, 326. It is conceivable that such issues had been discussed, inspired by Benedetti’s work, between Galileo, Mazzoni, and Del Monte during Del Monte’s stay in Tuscany in 1589. We would like to thank Pier Daniele Napolitani for drawing our attention to this possibility and to the above-mentioned passages.
Galilei 1960. For a thorough discussion of the chronology of these writings, see Giusti 1998.
See the extensive discussion in Galluzzi 1979.
Galilei 1968, vol. 2, 159: “Centro della gravità si diffinisce essere in ogni corpo grave quel punto, intorno al quale consistono parti di eguali momenti.” Translation in Galilei 1960, 151. See also Galilei 2002.
Galilei 1968, vol. 2, 164: “Un’altra cosa, prima che più oltre si proceda, bisogna che sia considerata; e questa è intorno alle distanze, nelle quali i gravi vengono appesi: per ciò che molto importa il sapere come s’intendano distanze eguali e diseguali, ed in somma in qual maniera devono misurarsi.” Translation in Galilei 1960, 156–157.
See Galilei 1968, vol. 2, 181. Translation in Galilei 1960, 173.
The knowledge that he had read it, however, is not entirely new. See Renn, Damerow, and Rieger 2001, 74.
