3.1 Benedetti Introduces His Physico-Mathematical Speculations
The Diversarum speculationum… liber is composed of six books, indicated as follows in the table of contents:
(1)“Arithmetic Theorems” (Theoremata arithmetica);
(2)“Explanation of the Operations of Perspective” (De rationibus operationum perspectivae);
(3)“Mechanics” (De mechanicis);
(4)“Disputations on Some Opinions Held by Aristotle
(5)“On Euclid’s
(6)“Epistolary Answers on Physics and Mathematics” (Physica et mathematica responsa per epistolas).
It should be noted that this partition of themes does not mirror the relative relevance of the issues according to the author. In fact, the length and the importance of the books does not exactly correspond to the subdivision indicated in the table of contents. Two sections are quite short: Book 2 on perspective and Book 5 on Euclid
The dedicatory epistle of the Diversae speculationes begins with an acknowledgment of the generosity of Emanule Filiberto
Following his example [that of the Duke] […] many asked my advice either in person or by mail on those mathematical problems. As I never avoid work in support of friends, it happened that, after so many years, looking at my paper boxes [scrinia] I found so many solved problems that they could be gathered in a fairly big volume.4
Benedetti expressed his admiration for the stimulating intellectual environment made possible by the magnificence of Carlo Emanuele I
Therefore, the glory [of your Highness] will equal that of the ancient Persian kings, and we can expect great happiness in this century if Plato’sprophecy is correct: the future State in which princes philosophize will be blissfully happy.5
Benedetti’s preface to the reader,6 following the dedicatory epistle, provides some more information related to his mathematical-physical work. The author repeats that the Diversae speculationes are a miscellanea of thoughts on various subjects brought about by his own curiosity or by that of patrons and friends. He declares himself confident that, in spite of their disordered format, his speculations will be considered useful, and makes a further claim for the absolute originality of his ideas: “non dubitans quin illis [meis scriptis] in illis scientiis aliquid commodi atque utilitatis allatura sint, praesertim cum in eiusmodi quaestionibus investigandis atque perpendendis, nemo (quod sciam) hactenus elaboraverit” (as I have no doubt that these [writings of mine] will bring something pleasant and useful, especially because (to my knowledge) nobody has so far sufficiently investigated and pondered such issues).7 The enthusiasm for novelty that was to motivate the supporters of modernity in the querelle des anciens et des moderns can be sensed in these words. Moreover, Benedetti does not exclude the possibility that different people, at different times and in different places, could have made the same discoveries by treating similar problems:
In fact, I included [traditum est] nothing in these books that, as far as I remember, I read or heard from others. If I picked up on the suggestions of others, either I offered a somehow different demonstration or I wrote on the same subject more clearly. In the case that somebody else wrote the same ideas [eadem tradidit], either I was not informed about this person’s speculations or the memory of these readings has vanished. Aristotlehimself remarked that it can easily happen that many come to the same ideas. It can even happen that, writing so much, I repeat a certain issue having forgotten that I already wrote on it. Indeed, this has happened to me a few times.8
Benedetti adds that very few people ever wrote books which are entirely and solely the fruit of their own mind, except perhaps for Archimedes
Benedetti envisages possible criticism of his work and seeks to anticipate objections with a remark inspired by a humanistic sense of relativism: “Quot capita, tot sententiae (As many heads, so many opinions).”9 Since a book will never receive universal approbation, he writes, it must suffice to provide fruitful insights which will encourage others to undertake further investigations. He mentions only three ancient models: Ptolemy
The letter to the reader ends up with a reflection on and a rebuttal of the principle of authority. Benedetti claims that mathematical and natural investigation should only be inspired by the love for truth. All considerations which do not derive from an open-minded philosophical attitude ought to be dismissed as unfounded:
In order to establish the truth, I occasionally had to oppose the opinions of others in many places, but I do not want you to ascribe it to some vice of mine nor to call me a malevolent and a sycophant as I display the errors of others. They should rather be thankful to me, since I aim to erase wrong opinions while I am dealing with the same issues—according to Antisthenes, it is indeed necessary “to begin by unlearning errors.” I show the truth, which all philosophers, beginning with Aristotle , should hold in higher esteem than any human authority or favor. As you will encounter something of this sort in my volume, I beg you to abandon all passions in your judgement, keeping in mind Sallust’s admonishment: “Those who assess controversial issues should avoid all hate, friendship, rage, and compassion.” Thus, always favor truth, which is worthy of the greatest efforts, instead of some person, as too many do. Hopefully you will benefit from my work and, in case you will pick some fruit, in the first place you should be thankful to Him from Whom all sciences descend.11
3.2 Mathematical Sections
Benedetti proved his capacity as a mathematician in his early writings, especially in the Resolutio omnium Euclidis
3.2.1 Geometrical Demonstrations for the Solutions of Arithmetic Problems
Two books of the Diversae speculationes are devoted to mathematics in the strict sense, Book 1 to arithmetics and Book 5 to proportions. Additionally, several letters in Book 6 are dedicated to mathematical problems and some metaphysical and physical issues are also treated as geometrical problems. In Book 4 Benedetti discusses examples such as the perfection of the circle, i. e., whether the circle, owing to its properties, has to be seen as the “first” or the “last” of the geometrical figures, and the possibility of a never-ending motion on a finite line or the possibility of an infinite motion on a finite line.
Book 1 of the Diversae speculationes has the form of a collection of mathematical exercises. Although Benedetti did not give them a systematic order, he claimed that his readers might find many useful explanations and remarks.13 He chose to call his propositions “theorems” instead of “problems” to stress their originality, as Benedetti believed they deserved higher recognition than mere problem-solving. He also apologized for the brevity of his treatment by saying that he had confidence in the intelligence and expertise of his readers (the same remark can be generalized for many other sections of the work). In Book 1 he approached arithmetic problems geometrically following Euclid’s
Moreover, Benedetti informs his reader about the process through which knowledge is acquired. In other words, his treatment is not restricted to theory but intentionally expands on heurstics. He complains that ancient mathematical knowledge was often transmitted in a very concise manner. It often lacked demonstration and definitions, or a clarification of the fundamental concepts. For this reason modern readers are often forced to investigate the hidden reasons of “the numbers” and “their effects,” with huge effort:
As we know, ancient mathematician-philosophers discovered many properties of the numbers but transmitted them to posterity either without reasons or with too few ones. Hence, several mathematical problems emerged, which have been addressed by the duke of Savoy. I consider some of the ensuing reflections on the ancients’ propositions to be worth transmitting to posterity. In this manner, my speculations will not fall in oblivion. Rather, I will offer to many an occasion to investigate abstruse themes which are entailed in problems and theorems and could hardly find an explanation so far.14
In order to examine Benedetti’s geometrical approach to arithmetic problems, let us consider theorem 120. Here is the problem:
The ancients already addressed this problem: three associates have an amount of money. The sum of the [money of] the first and the second is known, as well as the sum of the first and the third and the sum of the second and the third. From such three aggregates [the ancients] derived the particular [amount of money] of each one of them.15
Following a method of resolution, which Benedetti ascribes to Gemma Frisus
Gemma Frisussolves this problem applying the regula falsi [rule of the false]. I will follow the same path. Suppose that the addition of the first with the second is 50, that of the second with the third 70 and that of the first with the third 60. From those sums take any two, for instance 50 and 70, whose addition is 120. Subtract from this sum the other one, that is, 60. The result is 60. Its half is 30. This is the amount of money of the second associate. It you subtract this number from 70 (which is the addition of the second with the third) you will get 40. This is the amount of the third associate. Finally, from this number taken away from 60 you will be able to derive the amount of the first associate.16
If we express the problem in modern form, this is the set of equations Benedetti is dealing with:
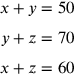
|
The algebraic solution devised by Benedetti is the following:
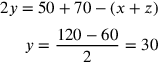
|
Thus,
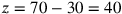
|
and
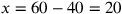
|
After this solution, Benedetti offers a geometrical demonstration of the validity of this procedure, referred to as “Gemma Frisus’s
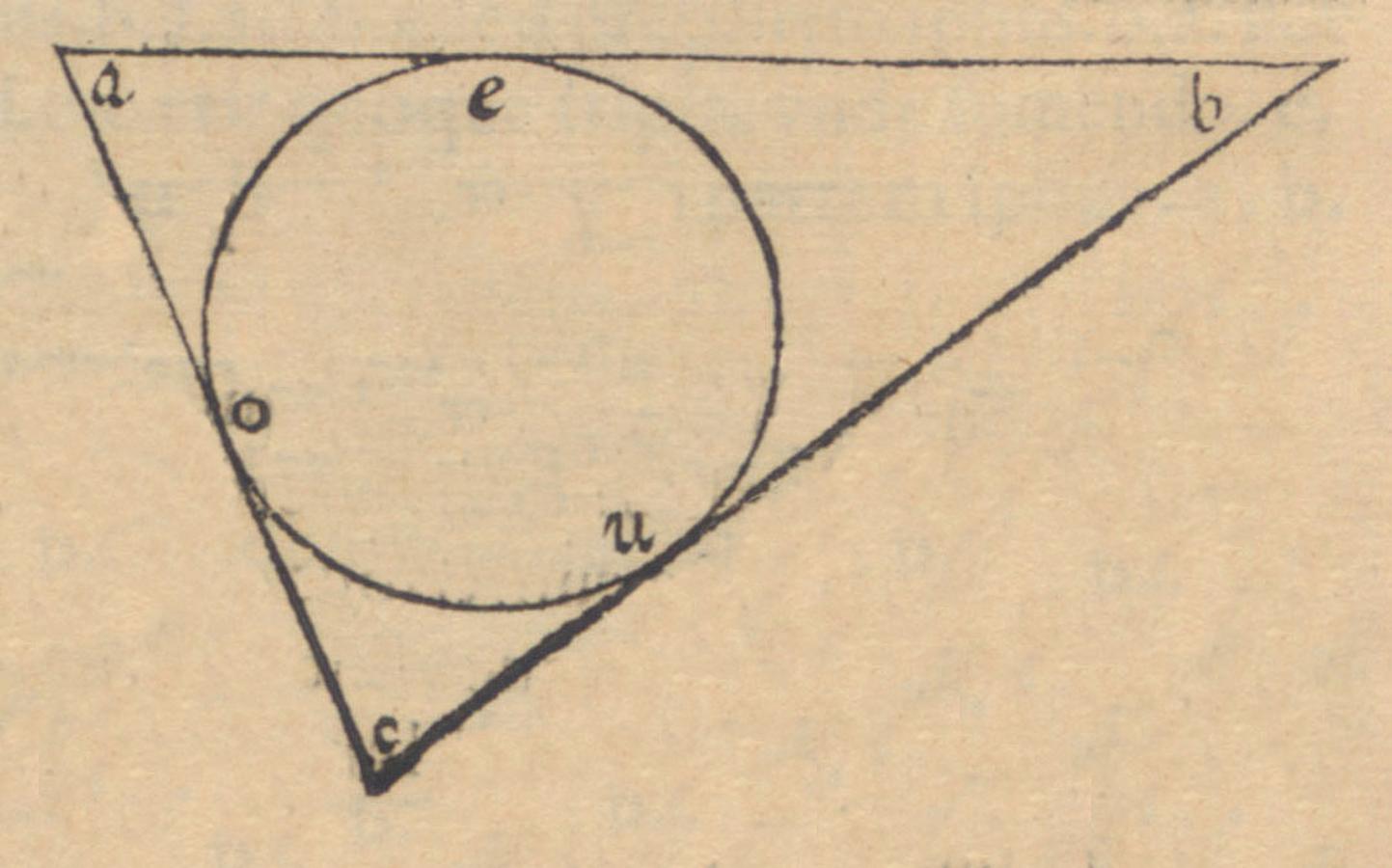
Fig. 3.1: Geometrical demonstration for the solution of a particular set of equations. Benedetti, Diversae speculationes, Book 1, Theorem 120, p. 82. (Max Planck Institute for the History of Science, Library)
Benedetti’s demonstration here follows:
In order to grasp this problem, let us consider the triangle here indicated as ABC each side of which corresponds to the addition of [the money of] two associates—for instance, assume that the side AB corresponds to the addition of the first with the second whereas the side BC to the addition of the second with the third and the side AC to the addition of the first with the third. Thereby AE, or AO, should be the number [i.e., the amount of money] of the first associate; EB, or BU, should be the second associate; and CU, or CO, should be the third. Furthermore, since AE is equal to AO, BE to BU and CU to CO, according to premises, if we derive the sum or side AC resulting from the addition of the side AB with BC corresponding to the other sums, we will know the addition of BE with BU. Hence, we will also know the half, which is BE or BU. Once we subtract it from the sum BA the resultant will give us the number [corresponding to] AE. By subtracting the number of AE, that is AO, from the sum (or side) AC, and [by subtracting] BU from BC we will know as a result OV and CU.17
We can (anachronistically) formalize Benedetti’s reasoning in the following manner.

|
The geometrical visualization of Frisus’s

|
This corresponds to the following addition:
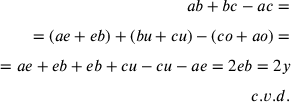
|
3.2.2 Theory of Proportions
Book 5 of the Diversae speculationes deals with the fifth book of Euclid’s
Hence, Benedetti proposed to introduce new postulates which he considered to be clearer (intellectui commodiora) in order to render the theorems that rely upon them more easily understandable (quandoquidem iis nostri postulatis admissis, sequentia Theoremata perfacillima reddentur). Actually, what he undertook was a revision of Euclid’s
Benedetti rephrases Euclid’s
[First:] All additions [composita] of an equal number of equal parts are equal. Similarly, all proportions are equal that result from the addition of an equal number of other proportions, which are equal among themselves. Euclidtries to demonstrate this in [Elements] V 22 and 23.
Second: If one subtracts equal parts from equal wholes, the remaining parts are equal among them. Conversely, if one adds equal parts to equal wholes, the additions will be equal among them. One should consider these considerations as referred to proportions.21
The postulates that follow (3–9) are Euclid’s
Bordiga underscored the didactic character of Benedetti’s treatment of Book 5 of the Elements by remarking that his concern about clarity and simplicity might have emerged from the teaching of mathematics to his princely pupils in Turin
The universal meaning of geometry as the foundation of rationality itself had been emphasized in the generation before Benedetti in an emphatic Encomium geometriae (Eulogy of Geometry) delivered by Girolamo Cardano
Benedetti agreed on the fundamental relevance of geometry as the cornerstone of natural inquiry. The fact that his treatment of proportions, although it was very short and condensed, was printed as a book in its own right in the Diversae speculationes bears witness to the relevance he attached to this part of mathematics. In fact, it was crucial for his treatment of weights and thus a close examination of Book 5 of the Elements was an indispensable premise of his mechanics. As Giusti emphasized, Benedetti’s treatment of composite propositions (relating to Euclid’s
3.3 The Geometrical Theory Underlying Linear Perspective
Book 2 of the Diversae speculationes, entitled De rationibus operationum perspectivae (Reasons of Perspective Operations), is a short treatise on linear perspective, that is, the optical discipline dealing with the construction of perspective to give the illusion of depth. Its main task was to recreate the “cone of vision.” Historically, it originated from the practical problems of three-dimensional representation in the fine arts but also had relevance for architecture (e.g., in surveying or in theoretical treatises), the military art (e.g., the derivation of the structure of the enemy’s fortification from a scout’s sketches), and found special application in theatrical stage scenery.
Benedetti’s book on perspective begins with a claim of originality: “To my knowledge nobody has so far taught the true and inner causes of the operations in perspective in an accomplished manner. Thus, I deemed it to be worth undertaking some reflection [disputationem] in this field.”28 The fact that “nobody” (nullus) has adequately treated perspective before is attested to by the great number of misunderstandings and widespread errors in this discipline: “In fact, many of those who prescribe the rules of such operations ignore the implications of the true causes, therefore they make various mistakes, as for instance in the following plane figure A [etc.].”29 Benedetti’s treatment was indeed different from the tradition of practical treatises (from Piero della Francesa’s
Like most parts of the Diversae speculationes, this book on perspective originated from extemporary sources of inspiration. In fact, it begins ex abrupto with the examination of an error in linear perspective which leads Benedetti to more general considerations. Moreover, the dedication of its seventh chapter to the architect Giacomo Soldati
The error discussed in the incipit of the De rationibus operationum perspectivae is represented in a two-dimensional figure (Figure 3.2).
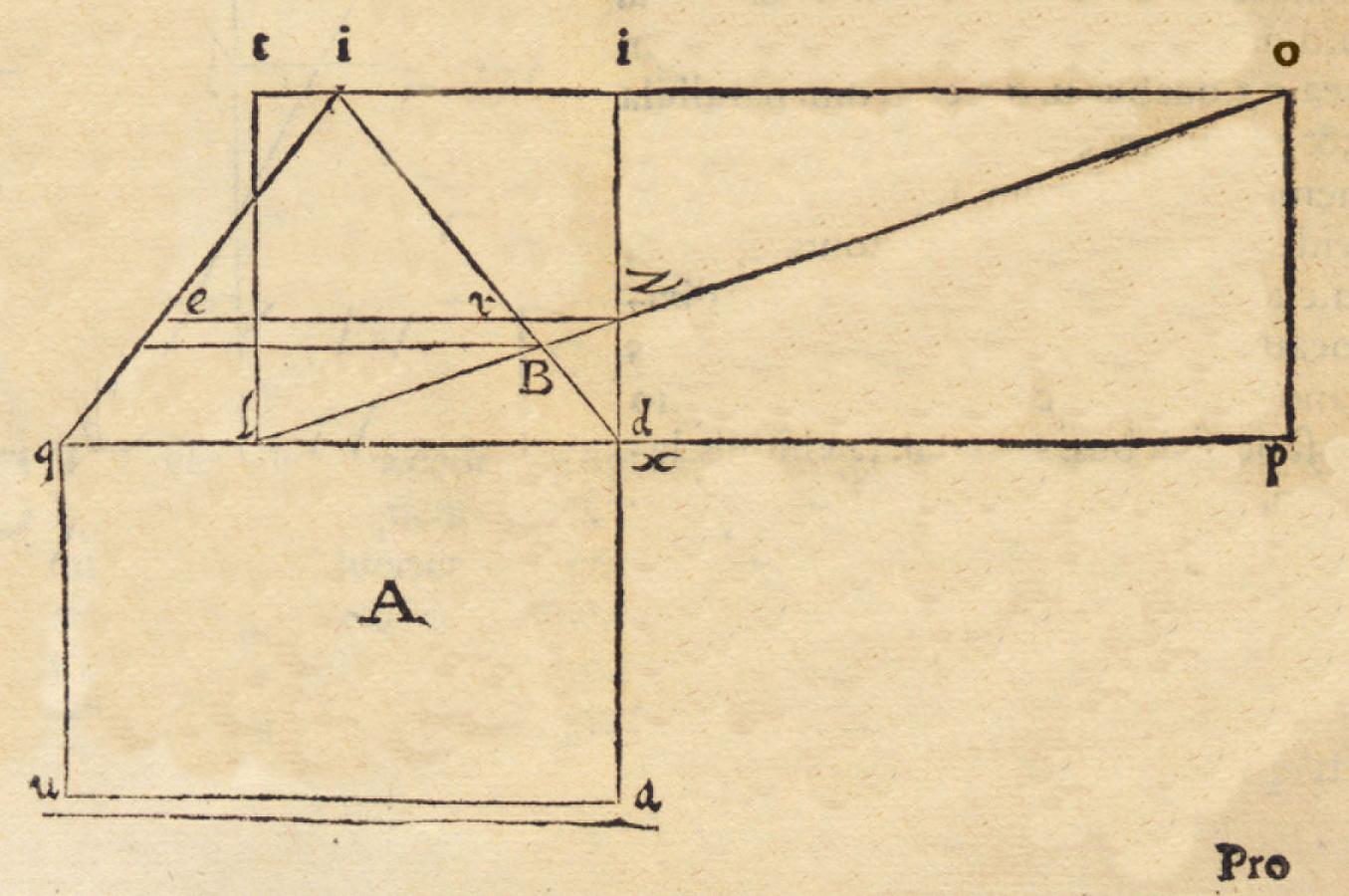
Fig. 3.2: Figura superficialis, or plane diagram, pointing out an error of linear perspective. From Benedetti, Diversae speculationes II, p. 119. (Max Planck Institute for the History of Science, Library)
Benedetti explains how to correctly construct the linear perspective “inscribed” in the given triangle IDQ:
[…] in the plane figure A (here included), in order to ’degradate’ (as one says) [i.e., to put it in perspective] the rectangle QA [QXAU] in the triangle IDQ, they [the practitioners] draw a line parallel to QD from point B (at the intersection of line OL with the side ID of the triangle) or, indifferently, they draw it from point Z (the intersection of the same OL with the perpendicular XI). They are not aware that the latter method is the only correct one, not the former. Conversely, if the former were correct, the latter could not be true. They might excuse themselves by arguing that one draws the aforesaid parallel line from B supposing that the plane IDQ is inclined horizontally relative to the rectangle QA according to the angle IDQ. But this excuse cannot be accepted because, according to their supposition, if one assumes that IDQ is inclined, the inferior angles of the rectangle put in perspective should not be as acute as IDQ and IQD. This can be easily understood considering their construction [ratio], which I show in the plane figure A here included. However, if one wants to see the rectangle in perspective, one should locate this plane relative to the eye in the same manner as the line ID relative to O. But this is too difficult [to represent].
To summarize, the correct manner [to put a rectangle in perspective] is to draw a line ER parallel to QD from point Z, which is common to OI and XI (perpendicular to LP).31
In order to visualize the construction, Benedetti produces an additional diagram (Figure 3.3) offering the tridimensional correspondent of the plane diagram he has just examined. Note that point O is the point of departure of the cone of sight. The observer is thus lying with his feet in point P.
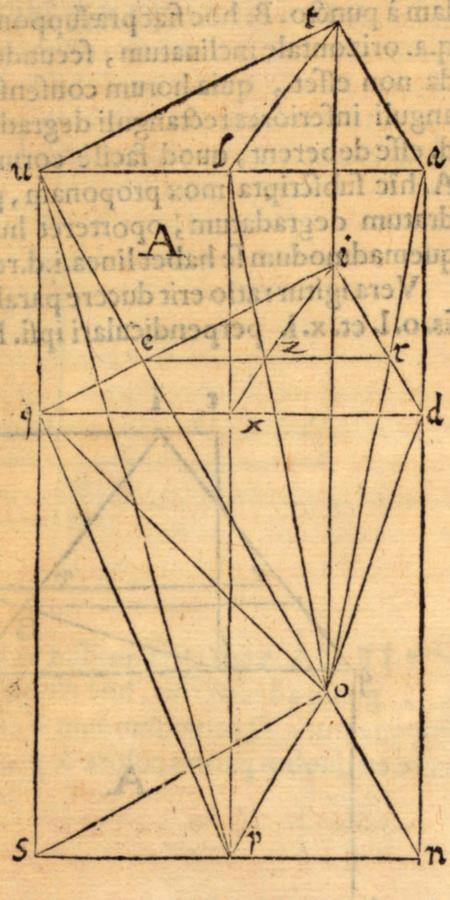
Fig. 3.3: Figura corporea, or tridimensional diagram, visualizing the same problem of linear perspective as in Figure 3.2. From Benedetti, Diversae speculationes II, p. 120. (Max Planck Institute for the History of Science, Library)
Departing from these considerations, Benedetti treats various cases (including the one in which the projection plane is not perpendicular to the observer’s line of sight) using the same approach. That is to say, he first draws bi-dimensional diagrams showing the construction and then offers tridimensional geometrical explanations providing an insight into the physical reality underlying the construction. He even offers a sort of virtual instrument to guide constructions in linear perspective.32 As Judith V. Field has argued, Benedetti “shows the applied mathematician’s concern with particular problems, rather than the pure mathematician’s interest in theoretical developments. The significance of his work lies not only in its mathematical insight but also in the fact that it shows us innovative work in the purest of sciences, namely pure mathematics, being carried out within an applied tradition.”33 As has been argued, it is plausible that Benedetti’s constructions were included in later works on perspective, in particular by Simon Stevin and Guidobaldo del Monte, although none of them explicitly referred to Benedetti. Apart from Del Monte’s enmity towards him, it was typical of Renaissance mathematicians who wrote on optics to leave their sources unmentioned.34
3.4 Sections on Physics: Mechanics and Natural Philosophy
Book 3 of the Diversae speculationes deals with mechanics. Benedetti remarks that many learned people have already written extensively on this issue, but that their achievements are not sufficient because nature and practice (usus) awaken many doubts concerning the validity and the completeness of previously acquired knowledge. New problems have emerged. His intention is to present many novelties and to propose theses that either have never been treated or have never been adequately demonstrated (nusquam ante hac tentata, aut satis exacte explicata). In the final words of his introduction to Book 3, we can see that he attaches great importance to his speculations on mechanics; he even states that he will be especially remembered after his death for his contribution to the advancement of this discipline:
Many man have written a great deal about mechanics, and they have written most ably. But nature and experience are always wont to bring to light something new or previously unknown. And it is therefore incumbent upon a high-minded and grateful individual, if he happens to discover something previously shrouded in darkness, not to begrudge it to posterity. For he himself gained a great deal from the work of others. Now it is my desire to publish a few items that will, I believe, prove not unwelcome to those who concern themselves with mechanics, items which have never before been dealt with or have not been sufficiently well explained. I may thus either show my desire to be helpful or at least give some evidence of possessing a bit of talent and industry. And perhaps in this way alone may I leave behind me proof that I ever lived at all.35
Book 4 essentially deals with Aristotle’s
We will treat books 3 and 4 of the Diversae speculationes separately and with particular attention (in chapters 5 and 6), owing to their historical and theoretical relevance.
3.5 The Epistles: Miscellanea Mirroring a Scientific Network
The last book of the Diversae speculationes is a large collection of letters, “Physica et mathematica responsa” (Epistolary Answers on Physics and Mathematics). The autonomy of this section is underscored by the insertion, at its beginning, of a second preface.
To the reader.
Nothing is more suited to virtue than being active and present through constant motion. Just like a shining star shimmering for the eyes of the spectators. It occurred to me that this or that person invited me with words or stimulated me with letters to dispute on those issues in which I am versed. In fact, I was devoted to mathematics and to highly philosophical speculations while I sojourned in the most splendid princely courts and illustrious cities, where many intelligent people displayed admirable curiosity, desire for knowledge and conversation. I collected part of those disputes and answers, because I judged them to be worth communicating. I planned to reread and revise them, if I had some spare time, [having in mind two goals]: on the one hand, that science itself circulates as much as possible and grows; on the other hand, that the names of those excellent men, who stimulated me with their questions, are made immortal, as far as it is in my power to do so, and that I can lead others to follow their example, abandon the idle sloth (which is able to corrupt even the most talented) and start investigating, exchanging, and discussing serious subjects that could prove useful at some point and worth disseminating. For the time being, please, approach our efforts with a benevolent and judicious attitude. Regards.36
Significant elements emerge from this passage: the courtly environment influencing Benedetti’s activity, the interest in applied knowledge, the recognition of the importance of dissemination, as well as the celebratory intention of the work (to render the dedicatees immortal). For us, this epistolary is the most tangible evidence of a network of social relations and its scope.
The epistles are not organized chronologically (actually the dates are almost always omitted) but rather according to the importance of the addressees, some of whom were already dead at the time of publication. The first letter was directed to the duke Emanuele Filiberto
Although it is not possible to identify all of Benedetti’s correspondents, one can say with certainty that most of the epistles are tied to the northern Italian environment, specifically to Turin
Among his correspondents, the list of Savoy
Benedetti had intense exchanges not only with patricians but also with artists, engineers, and practitioners. Four letters are addressed to the architect Gabriele Busca
Some epistles tackle the philosophical and epistemological issues underlying mathematics and their cognition. For instance, those to his Venetian
The identity, biographies, and work of many of Benedetti’s correspondents are still obscure. This is especially true for foreign scholars, presumably Germans, whose names were latinized as follows: Theodosius Raisestaim,
Footnotes
Benedetti 1585, f. A2r. Note that the pagination A1–A4 is doubled: the first installment A1–A4 contains frontispiece, table of contents, dedicatory epistle, and preface to the reader, whilst the second installment includes the first eight pages of the Theoremata arithmetica. Since the latter has also a pagination number (1–8) we will quote from the first fascicle indicating the folio and from the second giving the page.
Benedetti 1585, 1: “Interrogavit me Serenissimus Dux Sabaudiae, qua ratione cognosci posset scientifice et speculative (ut dicitur) productum ex duobus fractis numeris, quolibet producentium minus esse.”
Benedetti 1585, f. A2r: “Illiusque imitatione […] non pauci aut praesentes, aut per litteras me de his, atque illis mathematicis quaestionibus consuluerunt. Cumque ego nunquam laborem amicorum causa defugerim, evenit ut post tot annorum curricula, mea scrinia scrutatus, invenerim tot absolutas quaestiones, ut ex eis corpus mediocre effici posse videretur.”
Benedetti 1585, f. A2v: “Quare, et veterum Persarum Regum gloriam [tua celsitudo] aequavit, et nos veluti in spem certam faelicitatis huius saeculi induxit, si verum est Platonis vaticinium, beatam eam futuram Rempublicam in qua Principes philosophentur.”
The comparison between the Duke of Savoy and the ancient Persian kings is in line with an established Renaissance topos derived from classical sources, in particular Xenophon’s Life of Cyrus, as discussed by Vester 2007, 228-229.
Benedetti 1585, f. A3r: “Nihil enim his libris a me traditum est, quod aut legisse, aut ab aliis audivisse meminerim, nam si aliena attigi, ea, aut cum aliqua differentia demonstrationis, aut dilucidius scripsi, quod si forte alius eadem tradidit, aut eius lucubrationes ad me non pervenerunt, aut earum perlectionis memoria excidit. Ut etiam Aristoteles ipse sensit facile fieri potest, ut pluribus eaedem opiniones in mentem veniant. Immo multa scribendi evenire potest, ut cum iamdiu aliquid scripserit, iam oblitus, idem repetat, quod mihi etiam nonnunquam accidit.”
Benedetti 1585, ff. A3v–A4r: “Quoniam vero multis in locis accidit, ut veritatis iudicandae causa necesse mihi fuerit quorundam sententiis adversari nolim te hoc mihi vitio tribuere, meque hoc nomine carptorem maledicumque habere quod alienos errores aperiam, cum potius habenda sit mihi gratia, quod in iis interdum laborans (quae Antisthenes in disciplinis magis necessaria esse dixit, ut mala scilicet prius dediscantur) falsas opiniones evellere studeam, veritatemque ostendere, quam omnis philosophus, Aristotelis exemplo, pluris quam cuiusvis hominis authoritatem, aut gratiam facere debet. Cumque in hoc volumine aliquid eiusmodi legeris te oratum volo, ut in iudicando, affectum omnes exuas, Sallustianum illud prae oculis habens. Omnes qui de rebus dubiis consultant, ab odio, amicitia, ira, atque misericordia vacuos esse decet. Hinc fiet, ut non personae (ut multi solent) sed veritati, quae summo studio dignissima est, semper potius faveas. Vale nostrisque laboribus utere, si quem inde fructum, sicuti spero tuleris, illi precipue habes gratiam a quo omnes fluunt scientiae.”
Benedetti 1585, 1: “Praeclare multa veteres mathematici philosophi de numeris eorum effectibus excogitata posteris tradiderunt, quorum cum vix ullam rationem reddiderint, aut certe per exiguam, occasione diversorum problematum mihi Serenissimo Sabaudiae Duce propositorum praebita, de iis quae ab antiquis proposita fuerunt contemplanda nonnulla occurrerunt, quae posteritate commendare non inutile arbitratus sum, ne heae meae cogitationes interciderent, et occasionem praeberem quamplurimis abstrusa haec indagandi, quae problematibus et theorematibus involuta, vix aliquem qui evolveret nacta sunt.”
Benedetti 1585, 81: “Supponunt etiam antiqui tres socios nummos habere, quorum summa primi et secundi cognita sit, item summa primi et tertii cognita et summa secundi et tertii item cognita, atque ex huiusmodi tribus aggregatis veniunt in cognitionem particularem uniuscuiusque illorum.”
Benedetti 1585, 81: “Gema Frisus solvit hoc problema ex regula falsi. At ego tali ordine progredior. Sit verbi gratia, summa primi cum secundo 50 et secundi cum tertio 70 et primi cum tertio 60; harum trium summarum accipiantur duae quaevis, ut puta 50 et 70, quae coniunctae simul dabunt 120 a qua summa detrahatur reliqua, idest 60. Et restabit nobis 60, cuius medietas ergo 30, hoc est numerus nummorum secundi socii; quo numero detracto a 70 (hoc est a summa secundi cum tertio) remanebit 40, hoc est numerus tertii socii; et adhic numerus desumptus a 60 residuus ergo numerus primi socii.”
Benedetti 1585, 82: “Pro cuius ratione consideremus triangulum adhic subnotatum abc cuius unumquodque latus significet summam duorum sociorum, ut puta latus ab significet summam primi cum secundo, latus vero bc summam secundi cum tertio, latus autem ac summam primi cum tertio, et ae seu ao sit numerus primi socii, et eb vel bu sit secundi socii, et cu seu co sit tertii, cum autem ae aequalis sit ao et be aequalis bu et cu aequalis co ex supposito si de<su>mpta fuerit summa seu latus ac datum ex aggregato laterum ab cum bc reliquarum summarum, relinquet nobis cognitum aggregatum ex be cum bu. Quare et eius medietas be sive bu nobis cognita erit, qua detracta ex summa ba relinquetur nobis cognitus numerus ae, detracto vero numero ae hoc est ao ex ac summa, seu latus, aut bu ex bc remanebit oc seu cu cognitus.”
In Commandino’s Italian translation (Euclid 1575, ff. 63r–v), these definitions go as follows:
“V. Le grandezze si dicono essere nella medesima proporzione, la prima alla seconda, et la terza alla quarta, quando le ugualmente molteplici della prima, et della terza, o vero insieme avanzano le ugualmente molteplici della seconda, et della quarta secondo qual si voglia moltiplicatione, o vero insieme le pareggiano e vero insieme sono avanzate da loro.”
“VII. Quando delle ugualmente moltiplici, la moltiplice della prima vanterà la moltiplice della seconda, et la moltiplice della terza non avanzerà la moltiplice della quarta, allhora la prima alla seconda si dirà haver maggior proportione che la terza alla quarta.”
In Commandino’s Italian translation, these definitions go as follows. See Euclid 1575, f. 7r:
“II. Se alle cose uguali, si aggiungono cose uguali, tutte sono uguali fra loro.
III. Se dalle cose uguali si traggono cose uguali, etiamdio le rimanenti sono uguali tra loro.”
Benedetti 1585, 198: “[Primum.] Quod tota composita ex aequali numero partium aequalium, sunt invicem aequalia. Ut si quis diceret omnes proportiones quae compositae sunt ex aequali numero aliarum proportionum invicem aequalium, sunt etiam invicem aequales, quod Euclides conatur demonstrare in 22. et 23. quinti libri.
Secundum. Quod si a totis aequalibus detractae fuerint aequales partes, quae remanent eruntque partes invicem aequales. Et e converso si aequalibus aequalia addas composita erunt invicem aequalia. Quod in ipsis proportionibus hoc loco semper intelligendum est.”
Cf. Giusti 1993, 27 quoting from Antonio Nardi: “Il Benedetti, Geometra insigne non si accorse, che volendo riformare il 5° libro di Euclide, trascurò la definitione della uguale, e disuguale ragion, quale principio e fondamento dell’opera. Stupiscomi certo di tale inavertenza.”
Giusti 1993, 33: “D’altronde, l’interesse della teoria di Benedetti non sta nel risultato globale, ma soprattutto nel ruolo chiave della proporzione composta, e in particolare nella creazione di un algoritmo di calcolo agile ed elegante.” See Benedetti 1585, 202.
Benedetti 1585, 119: “Cum nullus adhuc (quod sciam) veras internasque causas operationis perspectivae perfecte docuerit, operaeprecium existimavi aliqua de iis disputationem suscipere.”
Benedetti 1585, 119: “Multi enim eorum, qui huiusmodi operationis regulas praescribunt, cum eius effectuum veras causas ignorent, varios diversosque errores committunt, ut exempli gratia in subscripta figura superficiali A [etc.].” See Figure 3.2.
Benedetti 1585, 133: “Superioribus diebus non diu postquam de perspectivis inter nos sermonem habuimus, dum animus totus adhuc in his esset. Illud in mentem venit quod eximius ille vir, et profundissimae doctrinae, nec unquam satis laudatis Daniel Barbarus se accepisse profitetur a Ioanne Zamberto patritio Veneto, qui ad verbum omnia desumpserat a Ioanne Cusino Parisiense. Nec parum mirabar peritissimus illum Cusinum, quod in capite quarto secundae partis perspectivae, ut quod piam planum quadrilatam composuisse. […].” See Mamino 1989.
Benedetti 1585, 119: “[…] in subscripta figura superficiali A volentes degradare (ut dicunt) rectangulum qa in triangulo idq ducunt parallelam ipsi qd a puncto B intersecationis lineae ol cum latere id trianguli, et (idem) indifferenter, eandem quoque a punctoque Z intersecationis ipsius ol cum perpendiculari xi ducunt, nescientes hunc solum esse verum modum, non item alium, quia si alius, talis esset, hic, verus non existeret, nam si vellent sese excusare, quod ducendo dictam parallelam a punctoque B hoc fiat praesupponendo planum ipsius idq versus rectangulum qa orizontale inclinatum, secundum angulus idq, haec excusatio accipienda non esset, quia horum consensu, praesupponendo planum idq inclinatum, anguli inferiores rectanguli degradati, non tam acuti, quae sunt duo idq et iqd esse deberent, quem facile eorum ratione innotescet, quae de figura corporea A hic subscripta mox proponam, praeter id, quod volentes deinde aspicere quadratum degradatum, oporteret huiusmodi planum respectu oculi ita collocare, quemadmodum se habet linea id respectu o quem factu nimis arduum esset.
Vera igitur ratio ergo ducere parallelam er ad qd a puncto Z communi ipsis ol et xi perpendiculari ipsi lp.”
Translation from Drake and Drabkin 1969, 166. Cf. Benedetti 1585, 141: “Scripserunt multi multa, et quidem scitissime, de mechanicis, at cum natura ususque, aliquid semper vel novum, vel latens in apertum emittere soleant, nec ingenui aut grati sit animi, posteri invidere, si quid ei contigerit comperuisse priis tenebris involutum: cum tam multa ipse ex aliorum diligentia sit consequutus. Paucula quaedam futura, ut reor, non ingrata his qui in hisce mechanicis versantur, nusquam ante hac tentata, aut satis exacte explicata in medium proferre voluit: quo vel iuvandi desiderium, vel saltem non ociosi ingenioli argumentum aliquod exhiberem: atque vel hoc uno modo me inter humanos vixisse testatum reinquerem.”
Benedetti 1585, 204: “Ad lectorem. Ut nil magis virtutis est proprium, quam agitari, et incessabili motu prodesse. Ac veluti fulgidum sydus ante oculus spectantium commicare. Ita mihi mathematicis iisque maxime philosophicis speculationibus dedito, saepissime, ut in principium summorum aulis, et amplissimis civitatibus degenti, ubi multa semper Nobilium mira curiositate, sciendi desiderio, et conferendi cupiditate referta, versantur, ingenia, contigit, modo ab his, modo ab illis, aut verbis tentari, aut literis provocari ad disserendum, de his, in quorum studiis versamur. Quarum concertationum et responsionum, quoniam non omnino indigna existimavi, quae memoria comendarentur, partem aliquam apud me conseruivi. Ubi vero per ocium licuit, relegi, ac tandem de manu mittere decrevi. Tum ut scientia ipsa quo magis diffundetur, crescat; et quicquid valeo, sine invidia in communem utilitatem conferam. Tum ut virorum praestantissimorum, qui me suis interrogationibus excitaverunt, quantum in me erit, gratitudine ergo, nomina reddam immortalia, et eorum exemplo alios, ocio sordidiore abiecto, quod solet iurialium praecipue excelsa ingenia corrumpere, ad sciscitandum conferendum, et disserendum, de rebus seriis, et quae usui aliquando esse possint, et quandoque evulgari mereantur, alliciam. Tu interim nostris laboribus fruere, et nostram diligentiam boni, et aequi consule, et Vale.”
“Mathematics” has to be here understood in the wide and interdisciplinary Renaissance meaning. It comprised arithmetic and geometry, as well as practical mechanics, architecture and engineering, astronomy and meteorology, optics, physics, and even metaphysical and epistemological issues.
Cecchini and Roero 2004, 32: “Dal quadro variegato dei temi discussi e dalle professioni dei protagonisti dei dibattiti emerge la figura di Giambattista Benedetti come uomo di cultura e di pratica, disposto ad instaurare un dialogo proficuo sia con esponenti del mondo scientifico in senso lato, come matematici, medici, giuristi e filosofi, sia con politici, diplomatici e ambasciatori, come pure con uomini d’arme e di religione, non disdegnando neppure architetti e artigiani, costruttori di strumenti e di fortificazioni, agrimensori e astrologi.” In the following we will often rely on Cecchini and Roero for an overview of Benedetti’s correspondents.
Benedetti 1585, 298 and 298–299. For the identification of this person, see Cecchini and Roero 2004, 58–59.
