Chapter structure
- 7.1 Sections of the Physical Disputations
- 7.2 An Archimedean Theory of Motion
- 7.3 On the Void: Atomistic Prospects
- 7.4 On Place: Space as intervallum corporeum
- 7.5 In Defense of Infinity
- 7.6 On Time: Toward an Absolute Frame for Physics
- 7.7 Natural and Violent Motions Revisited
- 7.8 The Cosmological Perspective of the Physical Disputations
- 7.9 An Evaluation: Benedetti’s Path to Natural Philosophy
- Footnotes
In this chapter we analyze Book 4 of the Diversae speculationes, entitled Disputationes de quibusdam placitis Aristotelis
7.1 Sections of the Physical Disputations
The Physical Disputations are a discussion of and an objection to Aristotle’s
One can conveniently subdivide the Physical Disputations into five sections (see table 7.1 below). The first twelve chapters are a lengthy discussion of Aristotle’s
Another subdivision (chapters 23–26, entirely translated in Drake and Drabkin 1969) deals with local motion and the shortcomings of the Aristotelian
We will concentrate on sections 1 (on motion), 3 (on the foundations of physics), and 5, part 2 (on cosmology). As one sees from our overview (table 7.1), the Physical Disputations are no less complex and heterogeneous than the volume of which they are part, the Diverse speculationes. Therefore, we will review Benedetti’s arguments in enough depth to enlighten the thematic interdependency and his approach in general, deliberately leaving aside an excessive analysis of details that would not help to understand his intellectual endeavor as a whole.
| Sections and their subjects | Chapters | Details | Presence in Drake and Drabkin 1969 |
|---|---|---|---|
| 1. Phys. IV 8 | §1–12 | Discussion on the void and down- and upward motion in different media | ✓ |
| 2. Phys. VII 5 | §13–18 | On the proportions of velocities, volumes, and surfaces | ✓ |
| 3. Foundations of physics revised | §19–22 | On the void (XIX ≈ Phys. IV 8), place (XX ≈ Phys. IV 4), the infinite (XXI ≈ Phys. III 5, De Caelo I,9 etc.,), and time (XXII) | Only §19 |
| 4. Violent and natural motion | §23–26 | Rejection of the Aristotelian |
✓ |
| 5. The sphere (geometrical and cosmological) | §27–34 | On the sphere (§29), on starry light (§30), on infinite motion (§31), on the Sun, its warmth and seasonal changes (§30–31 and §34), celestial music, and harmony (§32–33) | Only §28 and §29 |
| §35–39 | On the composition of circular and rectilinear motion and Copernicus’s |
✓ (only §38 missing) |
Tab. 7.1: An overview of the Physical Disputations and of their English translation in Drake and Drabkin 1969.
Tab. 7.1: An overview of the Physical Disputations and of their English translation in Drake and Drabkin 1969.
7.2 An Archimedean Theory of Motion
The Renaissance rediscovery of Archimedes’s
7.2.1 Aristotle’s Physics IV 8
Benedetti’s considerations on motion are presented as a criticism of Aristotle’s
But in vacancy […] nothing could go on moving unless it were carried. Nor (if it did move) could a reason be assigned why the projectile should ever stop—for why here more than there? It must therefore either not move at all, or continue its movement without limit, unless some stronger force impedes it.5
As far as motion is concerned, Aristotle
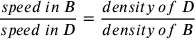
|
Furthermore:
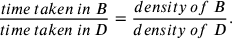
|
On this basis, Aristotle
According to Aristotle
What reason can be assigned for this greater velocity [of a heavier falling body]? If the passage is through a medium, there must be such a difference [in the velocity of fall between heavier and lighter bodies]; for when there is anything there to cleave, the body superior in force of its thrust will necessarily cleave the medium faster, since either its more suitable shape or the natural thrust it exercises, whether following its natural movement or being thrown, makes it cleave the better. Where there is nothing to cleave, therefore, all bodies will move at the same velocity; which is impossible.7
Aristotle
His must surely be a careless mind who does not wonder how it is that a small particle of the earth, if raised to a height and then set free, should refuse to remain where it was but begin to travel, and travel the quicker the bigger it is, whereas if one held the whole Earth in the air and let it go, it would not move. But in fact, for all its weight, it is at rest.8
This argument was repeated by Ptolemy
In summary, Physics IV 8 provides Benedetti with a series of entangled problems involving the void, infinity, and motion. He begins his reform of physics by dealing with the last issue and then moving to a treatment of the other ones. In relation to motion through a medium, he enlists some commonly accepted assumptions (primo verissima et obiecta intellectus per se cognita) in chapter 2:
Therefore, whenever two bodies are subjected to or receive one and the same resistance to [the motion of] their surfaces, [the speed of] their motions will turn out to be to each other in precisely the same proportion as their motive forces. And, conversely, whenever two bodies have one and the same heaviness or lightness, but are subject to different resistances, [the speed of] their motions will have the same ratio to each other as the inverse ratio of the resistances.10
The cases that have to be considered are basically two: first, different bodies in the same medium, and second, equal bodies in different media. A decisive difference between two bodies is their gravitas (gravity, weight) or levitas (lightness). For Benedetti, gravitas and levitas act as moving forces. He calls them virtutes moventes or facultates moventes. For the sake of brevity, we will refer to them as virtus/virtutes.
If we use V like velocitas for speed, P like pondus for virtus, and R like resistentia for resistance, we can formalize the previously mentioned general assumptions in the following way:11
I. Case in which R is constant:
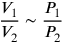
|
II. Case in which P is constant
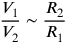
|
7.2.2 Speed in Different Media
Benedetti regards the Aristotelian
In the second disputatio, Benedetti declares that the virtus (weight or lightness)13 of a body varies depending on the densitas (density) of the medium. Here he has in mind the three different cases considered by Archimedes
Solids heavier than the fluid, when thrown into the fluid, will be driven down as far as they can sink, and they will be lighter in the fluid by the weight of a portion of the fluid having the same volume as the solid.14
The actual virtus (either weight or lightness) of a body results by subtracting from the total virtue (virtus totalis) a quantity which Benedetti calls resistentia extrinseca (resistance, for instance in disp. 9) and depends on the densitas (density, for instance in disp. 3), which we could regard as an expression indicating the specific weight:15
virtus in medio = virtus totalis – resistentia
Accordingly, he holds the position against Aristotle

|
Given this equation, Benedetti shows (chapters 3–4) that the thesis of Physics IV 8, namely that the ratio of the speeds is reciprocally proportional to that of the densities of the media, is only true in a special case, which can be constructed ad hoc: if the ratio of an object’s weight (or the corresponding speed) in one medium (for instance air) to its weight in another medium (for instance water) is equal to the ratio of the first medium (air) to the second (water). However, it is incorrect to claim that the ratio of the speeds of all bodies moving through different media remains the same. In chapter 6, Benedetti demonstrates moreover that the ratios of the weights (or speeds) of a body through different media are not maintained as constant in different media (Quod proportione ponderum eiusdem corporis in diversis mediis proportiones eorum mediorum densitatum non servant. Unde necessario inaequales proportiones velocitatum producuntur).16
We should now add some considerations on Benedetti’s argumentative strategy. He begins chapter 2 with a reference to principles generally taken for granted: primo verissima et obiecta intellectus per se cognita. The adverb “primo” can have two meanings in this context: it could indicate either that the author is proposing the “first” principles of the motion theory or, quite on the contrary, that he is presenting theses that are universally true “only at a first glance.” These “very true assumptions,” these primo verissima, are in fact the Aristotelian
7.2.3 Motion in pleno and in vacuo
After these considerations on motion in different media, Benedetti deals with the motion of bodies with different dimensions (but of the same material) through a medium as well as through the void. Chapter 7 considers the case in which two bodies A and O, made of the same matter and having the same figure, traverse the same medium. According to Aristotle
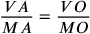
|
(according to Aristotle
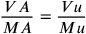
|
(case of two bodies with equal dimensions and different weights).
Since by assumption MO = Mu, it follows that Vu = VO, but this is not consistent with the assertion that two bodies of equal weights and different dimensions will move with different speeds in a medium because a bigger body needs more “force” to penetrate the medium than a smaller one:
The body which, when compared to the other, is of equal weight or lightness, but is subject to smaller resistance, moves [in natural motion] more swiftly than the other in the same proportion as its surface is subject to a smaller resistance than that of the other body, by reason of its being able more readily to divide the continuity of the air or water.18
Therefore, the ratio of the velocities of two bodies having equal material composition and figure but different dimensions is untenable, pace Aristotle
Chapter 9 introduces the issue of motion through the void, asserting, against Aristotle
In a plenum the ratio of the external resistances in the case of these bodies is subtracted from the ratio of the weights, so that the ratio of the speeds remains. And this last ratio would be annuled if the ratio of these resistances were equal to the ratio of the weights.19
The argumentation is not immediately intelligible to the modern reader. Contrary to appearance, in fact, this passage does not describe the following subtraction:
 (V is the speed, P the weight, and R the resistance).
(V is the speed, P the weight, and R the resistance).
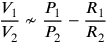
|
According to the theory of proportions, the addition and subtraction of a ratio to or from another ratio can be conveniently represented in a modern fashion as follows:20
I. Meaning of ratios addition:
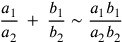
|
II. Ratios subtraction:
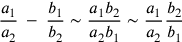
|
Given this, the relation indicated by Benedetti in the above-mentioned passage can be rendered through the following symbolic expression:
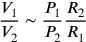
|
This relation expresses in a concise form the Aristotelian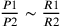 ). In fact, in this case (and only in this case) the speeds of bodies with different weights would be the same. As a consequence, there would be “no proportion” between different quantities but rather an equality of speeds. Benedetti indicates that this special case of motion in pleno, in which bodies with different weights have equal speeds, is the rule for motion in vacuo.
). In fact, in this case (and only in this case) the speeds of bodies with different weights would be the same. As a consequence, there would be “no proportion” between different quantities but rather an equality of speeds. Benedetti indicates that this special case of motion in pleno, in which bodies with different weights have equal speeds, is the rule for motion in vacuo.
Chapter 10 expands on motion in vacuo. It presents the famous thesis that bodies of the same material move with the same speed in vacuo, although they might have different dimensions. Benedetti remarks that a body O can be divided into halves A and E, each of the same weight (or virtus). If an ideally weightless bar connects them, the weight at the center of the connection should be the sum of the partial weights and thus equal O. Therefore, bodies composed of the same material will fall with the same speed, independently of their weight. In chapter 11, one reads that motion in pleno is different as a consequence of the friction of the medium, except for the special case in which the parts travel through media whose resistances have “the inverse proportion of the weighs” (si duo corpora… suas resistentias ad invicem proportionatas haberent, ut sunt eorum pondera).21
7.2.4 A Note on the Historical Relevance of Benedetti’s Reflections on Motion
Our analysis of the first part of the Physical Disputations should be sufficient to understand Benedetti’s approach to motion and the scope of his investigation. Subdivision two tackles Aristotle’s
Before we tackle these foundational aspects, we would like to recount the influence that Benedetti’s theory of motion exerted on the young Galileo
Moreoever, it should be remarked that the Copernican
7.3 On the Void: Atomistic Prospects
Benedetti’s considerations on motion are followed by a treatment of the void which, from the perspective of Aristotle’s
Hence, Benedetti reintroduces the concept of the void into physics, which was excluded by Aristotle
Among Benedetti’s contemporaries the most committed natural philosopher supporting atomism was Bruno
Epicure similarly nameth the whole and the universe a mixture of bodies and of the void; and in this universe and in the capacity thereof to contain the void and the empty, and furthermore in the multitude of the bodies contained therein he maintaineth that the nature of the world, which is infinite, doth exist.30
However, the concept of the void assumes in Bruno
First, the void refers to all which is not bodily and thus does not have the property of resisting penetration. In this sense, there is a “boundless ethereal region” (eterea regione inmensa), in which the worlds are plunged. The countless worlds populating the universe are themselves composed of matter and the void.32
Second, the void has the meaning of infinite space (spacio infinito). In it everything is included. It is the container that cannot be included in anything else.
Third, space can be assumed to be nothingness, in accordance with Aristotle
Bruno’s
Other Renaissance scholars supported combinations of atomism and heliocentric astronomy as well. A case in point is the circle of scientists gathered around Henry Percy
Atomism was to be embraced by celebrated exponents of sixteenth-century science and philosophy such as Galileo
Benedetti shared many ideas with contemporary and later scholars in his criticism of Aristotle’s
7.4 On Place: Space as intervallum corporeum
Chapter 20 of Benedetti’s Physical Disputations deals with the concept of place. Aristotle
That infinite places must exist, if place is [conceived of as] intervallum, is not inconvenient. In fact, just as any body can be [divided into] infinite bodies (which he [Aristotle] would call “in potentia”), so can any intervallum be [divided into] infinite intervalla as well.45
Benedetti is always brief in his treatment of philosophical issues and leaves much implicit. Therefore, the reader is challenged to reconstruct the complete vision implied in his short statements and critical points. Reference to Renaissance philosophical sources discussing the same theses from an Aristotelian
Other philosophers (and not unimportant but very reputed ones) asserted that there is void space among natural beings and that it is not only distinguished in essence [per sua natura] from the bodies it accommodates, but also it is so separated from them that it can remain completely naked and really deprived of them. Furthermore, many supposed that such a space (which is completely void, without any bodies) is mixed and situated between the beings of this world and their parts. Additionally, they believed that it infinitely extends outside the heavens. Thus, these philosophers considered the void to be that being which not only can be deprived of all bodies and substances […] but also is apt and capable of receiving the bodies, giving them a place (something which does not occur to lines, points, and other accidents). One of the main reasons for holding such doctrines was, as they said, that, if there is no space in nature (or a void place without bodies), the motion from place to place would be impossible, although the motion of alteration would be possible. In fact, all beings, in order to move to some other place, need some in-between space through which they can move. If this space were not void, it would be necessary that, as it is filled with other bodies, different bodies would penetrate each other while crossing that full space. And this is impossible.46
Thus Piccolomini
To sum up, Benedetti defines the locus, against Aristotle
7.5 In Defense of Infinity
Chapter 21 is devoted to infinity: Utrum bene Aristoteles
Additionally, Aristotle
The weakest argument brought forward by Aristotle
Aristotle’sarguments in the same part of Physics III 5 are even worse. He denies that infinity can be regarded as a quantity by saying that only one defined quantity is intelligible, such as a cubit, a three-cubit, etc. Thereby, he does not consider that in the same manner the quantity of infinite cubits is intelligible as well. Moreover, the definition of quantity does not imply limitation by necessity. For instance, the definition of number does not imply the necessity of any determined number, since an infinite multitude is not less intelligible than a finite.52
The last false Aristotelian
Like Bruno
In summary, in chapter 21 of the Physical Disputations, Benedetti defends the mathematical and physical possibility of the infinite. The question of the title “Whether Aristotle
7.6 On Time: Toward an Absolute Frame for Physics
Benedetti’s definition of tempus (time) is closely connected with that of locus (place). He deals with it in Physical Disputations, chapter 22, Exagitatur ab Aristotele
It should be noted as a preliminary remark that the understanding and definition of time was regarded as a natural as well as a psychological issue. This should not be surprising, since the doctrine of the soul, or psychologia, was an integral part of natural philosophy, or physica, in standard university curricula. A standard reference on time was the Timaeus, where Plato
Neither qualitative modification nor growth nor genesis has the kind of uniformity that rotation has; and so time is regarded as the rotation of the sphere, inasmuch as all other orders of motion are measured by it, and time itself is standardized by reference to it.56
For both philosophers, Plato
According to Benedetti’s criticism of Aristotle
It could seem to somebody that, to indicate [significare] a certain quantity of motion, one has to assume as much time as if one says, for instance, that a certain operation has been carried out in the space of two hours, or two days, or two years. Still, it should be remarked that this is not literally [simpliciter] true, since the imagination conceives the interval of two hours, days, or years as the motion of celestial bodies without which neither years, not days, not hours would exist, even though time is placed, so to speak, in time, just as a body in a place. Thus, motion is measured by motion and time by time, and not the one by the other.60
Benedetti claims that time, unlike motion, is eternal: “Necessarily, from a philosophical point of view, time is eternal and motion not.”61 Whereas a motion can be extinguished and a body can be at rest after a displacement, time goes on inexorably. It is always present to our senses and always escapes them because it is the never-ending passing of a single instant. Benedetti makes clear that he intends the instans to mean “one in species” (unum in specie), i.e., the essence underlying the vanishing flux of time that cannot be experienced in itself as a given and measurable succession (non in numero).62 This Augustinian
Just as a dense body occupies a lesser interval of place than a less dense [rarus] body, similarly a quick motion is accomplished [peragetur] in a shorter space of time than a slower motion.63
From this passage it is clear that Benedetti’s idea of place as intervallum corporeum goes in the direction of an empty homogeneous space which can be occupied by bodies of greater or lesser density. Time has the same absolute character as place. It can contain more or less rapid motions without being affected by them. Space and time or, more precisely, intervallum corporeum and tempus are objective and independent coordinates of natural phenomena.
In order to understand Benedetti’s considerations on time, it is useful to delve into the views of his immediate forerunners, in particular Cardano
7.6.1 Cardano’s Subtleties on Time
In the letter to the reader of the Diversae speculationes, Benedetti indicated Cardano
He introduces the problem of time in connection with his treatment of the dream (somnium), beginning with the question: “Why does time appear much longer while dreaming than in reality?”66 He reports that once he dreamed that he visited an unknown city far away from his home in Milan
It should be added that there is a passage of the Physics where Aristotle
Time cannot be disconnected from change; for when we experience no changes of consciousness, or, if we do, and are not aware of them, no time seems to have passed, any more than it did to the men in the fable who ‘slept with the heroes’ in Sardinia, when they awoke; for under such circumstances we fit the former ‘now’ to the later, making them one and the same and eliminating the interval between them, because we did not perceive it. So, just as there would be no time if there were no distinction between this ‘now’ and that ‘now,’ there appears to be no time between two ‘nows’ when we fail to distinguish between them. Since, then, we are not aware of time when we do not distinguish any change (the mind appearing to abide in a single indivisible and undifferentiated state), whereas if we perceive and distinguish changes, then we say that time has elapsed, it is clear that time cannot be disconnected from motion and change.68
These considerations are not aimed at isolating a subjective meaning of time by eliminating any objective references. Still, it is plausible that Cardano
This Augustinian
But what is time? Although nothing of it is ever [given], nonetheless everything is in it and it accompanies [assistit] everything always. It itself generates and destroys everything; it is the source [auctor] of life and death. Its expectation is always very long, while its memory is always very short. Although it is always with us, we never grasp it. Even though there is such an abundance of it, nonetheless no restoration [reparatio] of it is ever conceded, thence the waste of no other thing is greater or worse.69
In this passage, Cardano
Hence, for Cardano
Thus, we do not comprehend time but rather that which occurs, or occurred, and endures in it. But time itself per se is out of reach [ignotum] to the senses. In fact all that we know [about it] is constituted through imagination.71
Like Benedetti, Cardano
7.6.2 Scaliger’s Aristotelian Restoration
Scaliger
Scaliger
Scaliger
Since the quantity of time corresponds to that of a motion between a ‘here’ [ubi] and a ‘there’ [ubi], the ‘where’ [ubi] that we use for time is deduced [transumptum est], without inconvenience, from that ‘where’ [ubi] which, in fact, pertains to [a determination of] place [locus]. Actually, time is a transient now, whereas place is an enduring where [ubi].78
Scaliger’s
7.6.3 Benedetti and the Renaissance Concepts of Time
Our excursus on Renaissance concepts of time is far from exhaustive, but it helps us to grasp the scientific context out of which Benedetti’s own position emerged. It also permits us to point out some major problems in the conceptualization of time, in particular its subjective and objective dimensions. The interrelation between tempus and locus was at the center of the reflections, the debates, and even the polemics of scholars investigating nature from various angles. The debate on time and on its relation to motion has meanings that are, at the same time, physical (Benedetti), psychological-physiological (Cardano
Hence, time, which is the measure of all movements, mainly has to measure a motion that is the most regular and enables the measurement of all other [motions] that do not have the same regularity in their components. As this motion is that of the first heaven, one has to conclude that time (which is like [a property] of a substance [in proprio soggetto],) is first of all measured by it through that motion of the first mobile. Through it all other motions are ruled. Hence, although time can be called the rule and measure of any motion, it will be reasonable not to pluralize it alongside the plurality of motions. Rather, it will remain one and the same for the whole world, just as the first motion, which is its proper and true subject [soggetto], is singular.82
In the generation before Benedetti, Cardano
For Benedetti, as a mathematician advancing a new Archimedean
7.7 Natural and Violent Motions Revisited
After his revision of the physical concepts of the void, infinity, space, and time, Benedetti moves on to discard the Aristotelian
Chapter 24 is a refutation of a series of Aristotelian
Copernicus
7.8 The Cosmological Perspective of the Physical Disputations
The cosmological dimension of Benedetti’s anti-Aristotelian
7.8.1 Physico-Mathematical Astronomical Issues
The astronomical-cosmological section begins (chap. 28) with a reflection on the sphere that goes against the opinion of Aristotle
In the following chapters, Benedetti reviews a series of astronomical and meteorological issues on which he accused Aristotle
7.8.2 The Copernican Conclusion of the Physical Disputations
Chapter 35, Motum rectum curvo posse comparari (Straight and curvilinear motions are comparable), is a crucial chapter for our analysis, since it is here that Benedetti, almost at the end of his Physical Disputations, introduces the Copernican
The subject matter is the comparability of rectilinear and circular motion: “[Aristotle
Benedetti first appeals to Archimedes’s
These considerations offer Benedetti the occasion to expand on the velocity of celestial motions. According to the commonly held opinion (secundum opinionem cummunem), the heavens would have to cover an immense distance within the 24 hours of the daily rotation. Close to the equator, the sun would cover 1,000 Italian miles per minute and Saturn 260,000 miles per minute, not to speak of the rapidity of the fixed stars. The assumption of this inconvenient velocity would of course be avoided if one assumed “the most beautiful theory” (pulcherrima opinio) of Aristarchus
And as for the speed of the fixed stars situated near the equator, one may make one’s estimate, and, in fact, this will seem very difficult to some. But this difficulty does not occur in the most beautiful system of Aristarchusof Samos that has been so divinely expounded by Nicolaus Copernicus .95
From a Copernican
In the subsequent chapter (chap. 36), Benedetti reworks the doctrine of the doctissimus Aristarchus
Apart from that, as we have already seen, Benedetti proposes a bizarre transformation of the Copernican
If the system of the learned Aristarchusis correct, it will be perfectly logical for that which takes place in the case of the Moon to take place also in the case of any of the five other planets. Thus, just as the Moon with the help of its epicycles revolves around the Earth as if on the circumference of a certain other epicycle of which the Earth is like a natural center (i.e., in the middle), carried around the Sun by the sphere of annual motion, so too may Saturn, Jupiter, Mars, Venus and Mercury revolve about some body situated in the center of their major epicycle. And this body, also having some motion about its axis, may be opaque, possessing conditions like those of the Earth, with conditions on the epicycle in question similar to those on the lunar epicycles described.97
This conception could provide an explanation for the existence of planetary epicycles, whose physical tenability has been already stressed in the disputatio 23. We could also regard these views of Benedetti as a cosmological reading of Copernicus
With this rejection of the distinction betwee a sublunary and a heavenly realm, Benedetti’s criticism of Aristotelian
7.9 An Evaluation: Benedetti’s Path to Natural Philosophy
The Disputationes de quibusdam placitis Aristotelis
Let us summarize the Copernican considerations that could have influenced Benedetti and consider the extent to which he went beyond them. First of all, Copernicus
Many of these Copernican
Our analysis has shown that the heliocentric system is not the main issue at stake in the Physical Disputations, although that theory becomes part of a general program of reform for natural philosophy. Far from being a mere “Copernican
Footnotes
Paolo D’Alessantro and Pier Daniele Napolitani have emphasized the impact of its sixteenth-century reedition in their studies on the Latin reception of Archimedes: “Nel 1544 usciva a Basilea l’editio princeps greco-latina di gran parte dei testi di Archimede oggi noti. Senza tema di esagerare, si può sostenere che questo avvenimento – al pari della pubblicazione del De revolutionibus orbium coelestium di Niccolò Copernico, apparso l’anno precedente a Norimberga – abbia fornito impulso alla nascita della scienza moderna.” D’Alessandro and Napolitani 2012, 9.
See Omodeo 2015.
As has been argued in Exploring the Limits of Preclassical Mechanics, the wider conceptual framework of Archimedean theories of motion was in fact deeply rooted in Aristotelianism. See Damerow et al. 2004.
Drake and Drabkin 1969, 198. Cf. Benedetti 1585, 169: “Quotiescunque igitur duo corpora unam eandemque resistentiam ipsorum superficiebus, aut habebunt aut recipient, eorum motus inter seipsos eodem plane modo proportionati consurgent, quo erunt ipsorum virtutes moventes: et e converso, quotiescunque duo corpora unam eandemque gravitatem, aut levitatem, et diversas resistentias habebunt, eorum motus inter seipsos eandem proportionem sortientur, quam habebunt eorum resistentiae converso modo […].”
It should be remarked that this algebraic rendering of Benedetti’s thoughts does little justice to contemporary efforts to represent functional dependencies among different magnitudes with the help of the available mathematical techniques, such as compound proportions, as will become clear from the following discussion; see also Damerow et al. 2004.
In this passage, Benedetti employs the word pondus, but in the discussion he also talks of “lightness”; therefore, we prefer to use the term virtus movens or, more briefly, virtus, which is the term used by Benedetti.
See Benedetti 1585, 174: “dictis corporibus subtrahitur proportio resistentiarum extrinsecarum.” For a discussion of Benedetti’s employment of the termini ‘pondus,’ ‘densitas,’ and ‘resistentia,’ see Helbing 1987, 155–168.
The details, the text, and the notes in the English edition by Drake and Drabkin are clear enough, so we will not expand on these aspects here.
It corresponds to the above-mentioned equation:
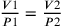 .
.
Drake and Drabkin 1969, 198. See Benedetti 1585, 169: “Corpus illud quod alteri comparatum, aequalis erit ponderis, aut levitatis, sed minoris resistentiae, existet velocius altero, in eadem proportione, cuius superficies resistentiam suscipit minorem ea quae alterius est corporis, ratione facilioris divisionis continuitatis aeris, aut aquae […].”
Drake and Drabkin 1969, 205. See Benedetti 1585, 174 (emphasis is ours): “In pleno dictis corporibus subtrahitur proportio resistentiarum extrinsecarum a proportione ponderum, ut velocitatum proportio remaneat, quae nulla esset, si dictarum resistentiarum proportio, ponderum proportioni aequalis esset, et hanc ob causam diversarum velocitatum proportionem in vacuo haberent ab ea, quae est in pleno.”
The same concept of addition and subtraction of ratios can be found in the manuscripts of Thomas Harriot, who called them “compositio” and “subductio” (or “compositio contraria”). See for instance Schemmel 2008, 635, reference letters g and o.
See Drake and Drabkin 1969, 206, n. 119: “Benedetti asserts that the speeds are equal only in the void, on the ground that in a plenum there would be an additional frictional resistance that would disturb this equality (unless this resistance itself were proportional to the weights of the bodies: Ch. 11).”
See Helbing 1987, 162.
Apart from Koyré 1986, see also Drabkin, “Introduction” to Galilei 1960, 9–10.
The ongoing debate between Galileo and Del Monte on the possibility of developing a mathematical dynamics is seen in Galileo’s letter of November 29, 1602: “V.S. Ill.ma scusi la mia importunità, se persisto in voler persuaderle vera la proposizione dei moti fatti in tempi uguali nella medesima quarta del cerchio; perché essendomi parsa sempre mirabile, hora viepiù mi pare, che da V.S. Ill.ma vien reputata come impossibile: onde io stimerei grand’errore e mancamento il mio, s’io permettessi che essa venisse repudiate dalla di lei speculazione, come quella che fusse falsa.” See Galilei 1968, 97.
See Benedetti 1585, 179.
On the medieval debates on the void and on the historical place of Galileo, and Benedetti before him, see Grant 1981, 60–66.
See Del Prete 1999, 61 and Michel 1962.
Bruno 2000a, 348: “[…] perché questo spirito, questo aria, questo etere non solamente è circa questi corpi, ma ancora penetra dentro tutti, e viene insito in ogni cosa.”
On his intellectual stature and achievement, see Schemmel 2008, who stressed that Harriot’s unpublished manuscripts reveal that his research activity was similar to that of Galileo in the same years. Moreover, Harriot’s reflections on infinity and the minimum bear witness to his familiarity with the work and ideas of Bruno. See Fox 2000 and Henry 1982.
For an overview of English science in that period, see Hill 1997, 15–76 and 118–200.
On medieval and early-modern corpuscular matter theories, see Lüthy, Murdoch, and Newman 2001. On Galileo, see Galluzzi 2011.
See Redondi 1983, chap. 7, 203–226. Also see Ariew 2013.
Galilei 1960, 47. See Galilei 1968, vol. I, 282: “[…] et ita non est necessarium, motum in vacuo fieri in instanti, sed in tempore minori quam sit motus in quovis pleno.”
Thus, Galluzzi’s remarks on the scientific production of the young Galileo could be conveniently extended to Benedetti (Galluzzi 2011, 19): “Il laboratorio del De motu antiquiora servì a Galieo per prendere definitivamente coscienza che la cosmologia e la fisica aristoteliche non potevano essere riformate con interventi limitati ad ambiti di indagine circoscritti. In particolare, lo scritto pisano evidenziava la raggiunta consapevolezza dell’importanza strategica di una radicale riforma della concezione aristotelica del movimento. Era questo, tra l’altro, l’ostacolo più serio da superare perché potesse essere accolta la visione copernicana, intesa non come semplice ipotesi matematica, ma come dottrina fisica. […] Né si può escludere che abbia tratto anche da esse [da tali problematiche] l’impulso per dedicarsi, con l’impegno proprietario esibito dai documenti dell’attività giovanile, all’impresa ambiziosa di una radicale riforma della concezione tradizionale del movimento e della struttura della materia.”
Benedetti 1585, 180: “Sed intervalla corporea aequalis a quavis figura terminata, continebunt semper corpora aequalia.”
Benedetti 1585, 181: “Et hoc modo nullum est corpus, quod in mundo aut extra mundum (dicat autem Aristoteles quicquid voluerit) locum suum non habeat.”
Drake and Drabkin 1969, 198. Cf. Benedetti 1585, 180: “Quod si locus intervallum esset, infinita loca existerent […] inconveniens [non] existit, quia eodem plane modo quo aliquod corpus potest esse infinita corpora (quod ipse diceret in potentia), sic etiam intervallum aliquod posset esse infinita intervalla.”
Piccolomini 1585, I 3, chap. 5, f. 44r: “Altri filosofi sono stati poi, et non già minimi, ma di gran fama, che han voluto che tra le cose della natura, si trovi spatio voto, non solamente distinto per sua natura dai corpi ch’egli riceve; ma intanto separato da quelli, che ignudo in tutto, et attualmente spogliato ne può restare. Né son mancati molti, che cotale spatio, voto in tutto d’ogni corpo, han posto, non solo meschiato, et interposto tra le cose che sono al mondo, e tra le parti loro; ma ancora fuor dei Cieli, infinitamente han creduto che si distenda. Questi filosofi adunque per il voto intendevano quella cosa, che non solo fusse privata d’ogni corpo et d’ogni sostanza […] ma fosse ancora atta, et capace, a ricevere i corpi, et dar lor luogo, il che delle linee, et de punti, et altri accidenti, non avviene. Tra le ragioni principali, che gli spingeva a credere una tal cosa, l’una era questa nella qual dicevano, che se non si potesse trovare tra le cose della natura spatio alcuno, o luogo voto d’ogni corpo; allora, se bene il movimento dell’alteratione potrebbe forse restare al mondo, tuttavia il movimento di luogo a luogo, non potrebbe senza ’l voto restar giammai. Conciosia c’havendo bisogno quella cosa, che ha da muoversi ad alcuno altro luogo, di alcuno spazio di mezo, per il quale si muova; se cotale spatio non fosse voto, saria forza che essendo pieno di altro corpo, nel passar per quello spatio pieno, venissero a penetrarsi più corpi insieme; adunque è cosa al tutto impossibile.”
Benedetti 1585, 180: “maximum inconveniens sequeretur, scilicet aequales locos capere inaequalia corpora, aut corpora aequalia, locos inaequales occupare.”
Benedetti 1585, 181: “Sed peius etiam sensit Aristotles eodem loco capitis quinti lib. 3 Physicorum, negando infinitum posse connumerari inter quantitates, dicens unam aliquam quantitatem intelligi ut cubitum, tricubitum, et cetera; ubi non considerat eadem etiam ratione intelligi posse aliquam quantitatem infinitorum cubitorum, et in quantitatis definitione nullam esse necessitatem terminorum, ut exempli gratia in definitione numeri, non est necessitas alicuius determinati numeri, quia multitudo, non minus infinita, quam finita, intelligi possit.”
Benedetti 1585, 181: “Ubi postea cap. 8 lib. 4 Physicorum ait nullam esse differentiam inter infinitum, et vacuum, revera nihil absurdius hoc dicere fingereve poterat.”
Plato Timaeus 37C–39E
Augustine 1988, XI 14, 265: “aliud sit motus corporis, aliud quo metimur quamdiu sit.”
Benedetti 1585, 183: “Tempus non erit mensura motus, sed motus quidem potest mensurare motum, videlicet velocior minus velocem, et brevior longiorem; et numerus mensuratur numero, et tempus tempore in quantum longum est, aut breve, non in quantum velox, aut tardum.”
Benedetti 1585, 182: “Si alicui videtur, quod ad significandam aliquam quantitatem motus, dicere huiusmodi operationem duarum horarum, aut duorum dierum, aut duorum annorum spatio completam esse, sit ponere tantum tempus, animadvertere debet hoc simpliciter non esse verum, quia horarum, dierum, et annorum intervalla, imaginatione concipiuntur ut motus corporum caelestium, sine quibus neque anni, neque dies, neque horae existerent, etiam si omnis motus sit (ut ita dicam) locatus in tempore, ut corpore in loco, unde motus motu, et tempus tempore, non autem aliud ab alio mensuratur.”
Benedetti 1585, 182: “Tempus ex necessitate, philosophice tamen loquendo, res est aeterna, motus non item.”
Benedetti 1585, 182: “Tempus igitur potius locus motus erit dicendum, quam numerus aut mensura eius, et tale est, ut consumatum videatur a continuo quodam fluxu unius instantis […] et cum dico ab uno instanti, unum in specie, et non in numero intelligo, quod a sensibus nostris percipi non potest, neque etiam notari, quia novum semper instans nobis occurrit.”
Benedetti 1585, 183: “Quemadmodum corpus densum occupat minus intervallum loci, contra quam fiat in corpore raro; sic etiam motus velox breviori temporis spatio peragetur, quam tardus.”
Cardano 1966, vol. 3, 651: “Cur somnium tempus longius multo ostendat quam sit.”
Cardano 1966, vol. 3, 651: “Contraria ratione tempus in somnio contrahitur, cum vel non somniamus […]: motus enim tempus est mensura.”
Cardano 1966, vol. 3, 651: “Sed quid tempus est? Cuius cum nihil unquam sit, omnia tamen in illo sint et semper omnibus assistit. Illud idem omnia generat et occidit, auctor vitae ac mortis. Utque illius expectatio longissima, ita semper memoria brevissima. Cumque nos semper comitetur, nunquam ipsum tamen agnoscimus. Nec cum eius tanta sit copia, reparatio tamen ulla conceditur: unde fit, ut nullius alterius rei iactura sit maior et vilior.”
Augustine 1988, XI 14, 238: “Quid est ergo tempus? Si nemo ex me querat, scio; si querenti explicare velim, nescio.”
Cardano 1966, vol. 3, 651: “Ergo nos non tempus, sed quod in eo fit, factumque est, atque manet, comprehendimus. Tempus vero ipsum per se est sensui ignotum: nam imaginatione constat quod a nobis cognoscitur.”
Scaliger 1557, f. 458v: “Hoc quidem ab omnibus iactatur: pauci introspectant.”
Scaliger 1557, f. 458v: “Nostri sane motus mensura sit: primi motus mensura non erit.”
Scaliger 1557, f. 458v: “At tempus est posterius motu primo. Est nimirum affectus eius, ab illo pendens.”
Scaliger 1557, f. 458v: “Tempus, inquit, aut est idem, quod motus, aut affectus eius.”
Scaliger 1557, f. 458v: “Tempus esse mensuram motus, et vicissim motum mensuram temporis.”
Scaliger 1557, f. 458v: “[…] dicimus tot partes aequinoctialis tanto moveri tempore.”
Scaliger 1557, f. 458v (punctuation and emphases have been standardized and modernized): “Quia tempus tantum est, quantus est motus inter ‘ubi’ et ‘ubi’ in loco. Iccirco ‘ubi’ quod pro tempore usurpamus, transumptum est, haud iniuria, ab eo ‘ubi’ quod est vere loci. Erit ergo tempus nunc fluens; et locus erit ubi continuatum.”
Scaliger 1557, f. 458v: “Cum enim tempus sit quantitas, nihil agit.”
Scaliger 1557, f. 458v: “[…] vita nostra est actus animae: in quem nihil habet tempus aut iuris, aut imperii.”
Scaliger 1557, f. 459r, Exercitatio 353, “De tua visione.”
Piccolomini 1585, I 3, chap. 7, ff. 52v–53r: “Di qui è, che’l tempo, c’ha da esser la misura di tutti i movimenti, bisogna che principalmente si applichi a misurare alcun movimento regolato sopra tutti gli altri, mediante il quale possa poi far da misura de gli altri tutti, che tal regola […] non hanno nelle parti loro. E tal movimento […] essendo […] quello del primo Cielo: si deve concludere, che’l tempo sia come in proprio soggetto da lui primamente misurato, nel detto movimento del mobil primo: mediante il quale, regolandosi tutti gli altri movimenti: ragionevol cosa sarà, che’l tempo, se ben si può chiamar regola, et misura d’ogni movimento, come di sopra habbiam lungamente detto, tuttavia egli non si multiplichi con la multiplicatione delli movimenti, ma resi uno stesso per tutto il mondo, sì come uno solo è quel movimento primo, che è il proprio, et vero soggetto suo.”
Benedetti 1585, 183: “[…] ut accidit lineae directionis, & retrogradationis planetarum, unde circulus uan erit ut epiciclus et b ut terrae centrum.”
Pierre Duhem pointed out the tension between physical and mathematical astronomy, albeit in a very inadequate way. See Duhem 1908. For a better understanding of the matter, see Di Bono 1990.
Piccolomini argues as follows: “Non è a punto manco sconvenevole il concedere cotale infinità in qual si voglia corpo semplice, che o salendo, o scendendo si muova per retta linea; che si sia veduto disopra esser di quello che in circolo si rivolge. Percioche essendo il partirsi salendo dal mezo dell’universo, e’ l venir discendendo a quello, che movimenti di luogo a luogo tra di lor contrarii: e ricercando li contrarii movimenti, luoghi contrarii parimenti; confessaremo esser opposti tra di loro il luogo disopra e questo qua giù da basso. E perché sempre tra due contrarii, se l’uno e per natura sua finito, e determinato, non sopporta il giustissimo governo della natura, che l’altro sia infinito e senza termine, secondo che discorrendo per tutte le contrarietà si può vedere.” See Piccolomini 1585, II 2, chap. 3, f. 24v.
One can compare the text of Benedetti, Diversae speculationes, disp. XXV, with that of Copernicus, De revolutionibus, I 8. The latter wrote: “Igitur quod aiunt, simplicis corporis esse motum simplicem (de circulari in primis verificatur) quamdiu corpus simplex in loco suo naturali, ac unitate sua permanserit. In loco, siquidem non alius, quam circularis est motus, quo manet in se totus quiescenti similis. Rectus autem supervenit iis, quae a loco suo naturali peregrinantur, vel extruduntur, vel quomodolibet extra ipsum sunt. Nihil autem ordinationi totius et formae mundi, tantum repugnat, quantum extra locum suum esse. Rectus ergo motus non accidit, nisi rebus non recte se habentibus, neque perfectis secundum naturam, dum separantur a suo toto, et eius deserunt unitatem.”
Benedetti 1585, 185: “Quod autem perfectum est, licet natura sit primum, est tamen ultimum generatione.”
Benedetti 1585, 185–186: “Circulus sphaeraque non ex uno solo angulo recto constat, ut idem Aristoteles putat […] sed sunt figurae infinitorum angulorum rectorum, et hanc ob causam a me dicuntur ultimae et perfectae, quia infinito nihil addi potest.” The authors would like to thank here Irina Tupikova for suggesting this interpretation of Benedetti’s argument.
The Pythagorean harmony was ridiculed by Alessandro Piccolomini among others. See Piccolomini 1585, II 4, chap. 12, “Del suono, et armonia, che i pitagorici pensavano, che nascesse per li movimenti de’ corpi celesti,” f. 105v: “[…] Quando i corpi celesti movendosi facesser suono avvenir dovrebbe a noi poscia che da si alto, et soverchio strepito, et sproportionato all’odito nostro quasi assordati, né quello né altro suono che qua giù si faccia, odire in modo alcuno dovremmo giamai. Per la qual cosa essendo manifesto che tante diversità di strepiti, che tra questi corpi inferiori si fanno, ancora che piccolissimi sieno, son da noi odite distintamente, è forza dire, per la ragione ultimamente fatta che né suono, né armonia, non può causarsi per li movimenti de gli Orbi, o delle stelle che volgendosi faccin la su in cielo.”
Benedetti 1585, 194: “[Aristoteles] recte dicere non potest motum rectum ad curvum comparabilem non esse 4. cap. lib. 7 Physicorum ubi errat quoque dicens reperiri non posse lineam aliquam rectam alicuius circuli circunferentiae aequalem.”
Drake and Drabkin 1969, 220. Cf. Benedetti 1585, 194: “Si igitur dicta quadratura dari potest, potest etiam dari una recta linea aequalis circunferentiae eiusdem circuli.”
Drake and Drabkin 1969, 221. Cf. Benedetti 1585, 195: “Et amplius de stellis autem fixis circa aequatorem posits quivis cogitet; quod revera difficillimum quibusdam videbitur, quod quidem non occurrit secundum pulcherrimam Aristarchi Samii opinionem, divinitus a Nicolao Copernico expressam, contra quam nil plane valent rationes ab Aristotele, neque etiam a Ptolomeo propositae.”
Drake and Drabkin 1969, 222. Cf. Benedetti 1585, 195–196: “Si doctissimi Aristarchi opinio est vera, rationi quoque consentaneum erit maxime, ut quod Lunae contingit, cuilibet etiam ex aliis quinque planetis eveniat, idest, ut quemadmodum Luna suorum epicyclorum ope circum terram volvitur, quasi per circunferentiam alterius cuiusdam epicycli, in quo terra sit instar centri naturalis (idest sit in medio) delati ab orbe annuo circa Solem; sic etiam Saturnus, Iupiter, Mars, Venus, atque Mercurius, circum aliquod corpus in medio sui epicicli maioris, situm habens, volvantur; quod quidem corpus, et aliquem quoque habeat motum circa suum axem, sit opacum, iis conditionibus, quae terrae sunt similes, praeditum existat, et in dicto epyciclo sint res similes istis lunaribus.”
