sit quadratum ipsius .D.B. Nunc supponendo .A.B. simile .a.b. clarum erit ex diffini-
tione similium figurarum, quod eadem proportio erit .A.D. ad .D.B. quae .a.d. ad .d.
b. hoc est .A.D. ad .D.C. ut .a.d. ad .d.c. hoc est .A.B. ad .B.c. ut .a.b. ad .b.c. ex prima
sexti, vel .18. seu .19. septimi, tunc cum dixerimus si .a.b. ita respondet ad .b.c. ergo .A.
B. correspondet etiam ita ad .B.C. quare ex regula de tribus recte fit multiplicando .
A.B. per .b.c. productum vero dividendo per .a.b. ex .15. sexti vel .20. septimi, cuius
proventus radix quadrata erit quod quaerebatur.
Sed aliter idem posse fieri speculatus sum, hoc est multiplicando numerum .49.
ordinis .1000. hominum cum radice quadrata numeri .3500. propositi, productum ve-
ro dividere per radicem quadratam ipsius .1000. unde proventus .91. erit numerus
unius ordinis .3500. numeri propositi.
Cuius operationis speculatio est ista.
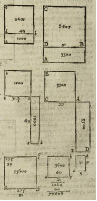
[Figure 314]
radix et .a.d. rectangulum proposi-
tum ipsius .1000. et .a.e. unus ordo.
Sit etiam .A.B. quadratum .3500. &
A.C. eius radix et .A.D. rectangulum
ipsius numeri .3500. propositi, simile
tamen rectangulo .a.d. et .A.E. eius
unus ordo. cum enim .a.b. aequale sit
a.d. et .A.B: A.D. tunc .a.c. erit media
proportionalis inter .a.e. et .e.d. & sic
A.C. erit etiam media proportiona
lis inter .A.E. et .E.D. per .16. sexti,
seu .20. septimi, & quia proporrio. A
E. ad .E.D. aequalis est proportioni .
a.e. ad .e.d. cum .A.D. supponatur si-
mile .a.d. ergo proportio .A.E. ad .A
C. aequalis erit proportioni .a.e. ad .a.
c. quae medietates sunt totorum aequa-
lium, recte igitur fiet si procedamus
ex regula de tribus, dicendo si .a.c.
correspondet .a.e. tùc .A.C. correspon
det .A.E. ex supradictis .15. sexti. vel
20. septimi.
Ratio vero quarti quaesiti per se
patet, quod est inuenire pavimentum
seu aream quadratam, in qua possint
locari quot homines volueris, ita in
ter se siti, ut unusquisque occupet .
7. pedes ipsius areae in longitudinem
et .3. per latitudinem a lateribus.
Seu ex proposito hominum nume
ro inuenire numerum ipsorum loca-
bilem in aliqua area quadrata, ita,
ut unusquisque occupet .21. pedes
quadratos ipsius areae.

