De inuentione axis proposite portionis datae sphaerae.
AD EUNDEM.
UTaxem propositae alicuius datae sphaerae inuenire possis ita tibi operandum est
ut gratia exempli. Proposita nobis est sphaera .c.i.e.t. diametri cognitae. pro
posita etiam est nobis eius portio .n.e.u. axis .e.a. cognitae minoris semidiametro, da-
ta etiam nobis est proportio alterius portionis minoris hemisphaerio .i.e.t. ad por-
tionem .n.e.u. quaeritur nunc quantus sit axis .e.x. secundae portionis hoc est desidera-
mus cognoscere proportionem .e.x. ad .e.a. vel ad diametrum ipsius spherae.
Cuius gratia reperiatur primo proportio circunferentiae maioris circuli ipsius sphae-
rae adeius diametrum, quae fere est ut .22. ad .7. ex Archimede.
Quo facto, inueniatur quantitas superficialis huiusmodi maioris circuli, quae sem-
per aequalis est producto quod fit ex semidiametro in dimidium circunferentiae ip-
fius circuli, ex eodem Archimede. Et sic cognoscemus quartam partem superficiei
sphaericae sphaerae proposite ex .31. primi lib. de sphaera, & cyllindro Archimedis.
Deinde sumatur tertia pars producti, quod fit ex semidiametro in superficiem
maioris circuli, & habebimus conum, cuius basis erit circulus maior, altitudo vero
semidiameter propositae sphaerae ex .9. duodecimi Eucli.
Quadruplum postea huiusmodi coni, erit quantitas soliditatis, seu corporeitas to
tius sphaerae ex .32. dicti lib. Archimedis.
Imaginemur postea in sphaerica portione .n.e.u. lineam .e.u. a summitate ad extremitatem
basis, cuius .e.u. quantitatem cognoscemus, hoc modo scilicet, fumendo radicem qua-
dratam producti .c.e. in .e.a. eo quod
quadratum .e.u. aequale est quadrato
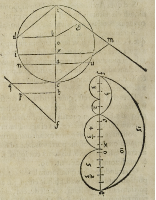
[Figure 308]
primi Eucli. hoc est producto quod
fit ex .c.a. in .a.e. ex .34. tertii eiusdem,
& quadrato .a.e. hoc est producto,
quod fit ex .c.e. in .e.a. ex .3. secundi
eiusdem.
Inuenta postea .e.u. ponamus eam
unius circuli semidiametrum esse, cu
ius superficialis quantitas etiam inue
niatur, ut supra dictum est, quae qui
dem aequalis erit superficiei portionis
n.e.u. ex .40. primi li. Archimedis de
sphaera, & cyllindro.
Haec autem quantitas ultimo inuem
ta multiplicetur cum tertia parte se-
midiametri datae sphaerae, & habebi-
mus soliditatem unius coni aequalis
aggregato soliditatis portionis .n.e.
u. simul sumptae, cum soliditate unius co
ni, cuius axis sit .a.o. residuum semidia-
metri nostrae sphaerae dempta .a.e. ba

