Figuram superficialem ellipsi similem, ex datis axibus cir-
cino mediante delineari posse.
AD EUNDEM.
FIguram superficialem ellipsi similem, ex datis axibus, circino mediante delinea
re cum volueris, ita facito.
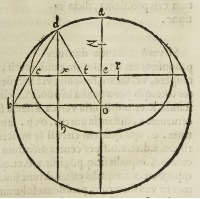
Sit .e.c. semiaxis maior .a.e. vero minor, ad angulum rectum inuicem coniuncti,
tunc .a.e. producatur usque ad .o. Itaq; .a.o. maior sit quam distantia inter .o. et .c. quae
quidem .a.o. posset etiam dari, describatur postea circulus .a.d.b. circa centrum .o. a
quo puncto protrahatur semidiameter .o.b. quae cum .a.o. angulum rectum consti-
tuat, quae .o.b. erit aequidistans .e.c. ex .28. primi, ducatur postea .b.c.d. et .o.t.d. unde
angulus .t.c.d. aequalis erit angulo .o.b.d. ex .29. eiusdem. ex quinta autem anguli .b.
et .d. sunt inuicem aequales, quare etiam
& anguli .d. et .c. inuicem aequales erunt,
[Figure 306]
tur postea .d.x.h. perpendicularis lineae .c.
e. ita distans sub ipsa .c.e. ut arcus circula-
ris circa .t. delineatus ex semidiametro .t.
d. aptus sit eam secare, sumpto postea .r.
tam distante ab .e. ut .t. reperitur ab ipso
e. et .z. ab .e. ut .o. ab eodem, ducendo po-
stea duos alios arcus magnitudinis priorum
circa centra .r. et .z. habebimus proposi-
tum.
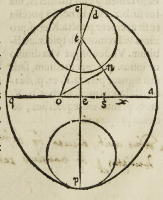
Sed cum quis voluerit prius arcus mi-
norum circulorum delineare circa maio-
rem axem, fiant cuiusuis magnitudinis, ut
in secunda figura videre est, posito tamen quod eorum diameter, minor sit minore
axe ipsius figurae, quorum circulorum unus sit .c.d. circa .t. eius centrum, deinde in axe
minori sumatur .a.x. aequalis .c.t. & protrahatur .t.x. quae per aequalia dividatur in pun-
cto .n. a quo postea ducatur .n.o. ad angulos rectos
[Figure 307]
cto .o. minori axi producta cum oportuerit, quod
quidem punctum .o. centrum erit arcus .d.a. maio-
ris, eo quod .o.t. aequalis esset .o.x. ex .4. primi Eu-
cli. unde .o.d. aequalis esset .o.a. & circuli etiam in-
uicem contingentes in puncto .d. ex .11. tertii tam
in prima, quam in secunda figura, sumpto deniq;
puncto .s. tam remoto ab .e. quam .o. reperitur ab
eodem, ipsum, centrum erit alterius arcus opposi-
ti, possemus etiam absq; divisione ipsius, t.x. consti
tuere angulum .x.t.o. aequalem angulo .t.x.o. unde ex
6. primi haberemus .o.t. aequalem .o.x.

