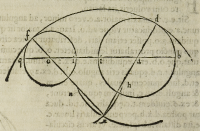
Sed si circuli propositi seiuncti fuerint, sumatur .b.i. diameter maioris, qui fiat se-
midiameter unius circuli circa centrum .o. & hic circulus vocetur .h.x. coniunga-
tur deinde semidiameter .o.i. minoris circuli cum semidiametro .a.i. circuli maio-
ris, & ex huiusmodi composita linea, fiat unus semidiameter .a.x. circuli .x.n. concen
trici cum maiori, & a puncto .x. intersectionis horum circulorum (posito quod se in-
uicem intersecent) ducantur per eorum centra .x.a. et .x.o. usque ad ipsorum circun-
ferentias in punctis .d. et .f. duae
lineae, unde habebimus .x.d.
aequalem .x.f. eo quod tam in
[Figure 304]
diametri, & semidiametri am-
borum circulorum, facto deni
que centro .x. unius circuli, cu
ius semidiameter aequalis sit
uni earum .x.d. vel .x.f. folu-
tum erit problema, dicta ra-
tione.
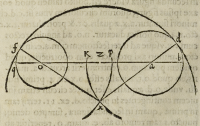
Si vero distantia duorum
propositorum circulorum tanta fuerit, quod secundi circuli nequeant se inuicem
tangere, vel secare, tunc alia via incedendum erit, quae talis est & generalis. Divida-
tur tota .q.b. per aequalia in puncto .z. circa quod signentur duo puncta ab ipso aequidi
stantia .K. et .p. distantia vero .a.K. facta sit semidiameter esse unius circuli .K.x. circa
centrum .a. distantia autem .o.p. semidiameter alterius circuli .p.x. circa cen-
trum .o. qui quidem circuli se inuicem secent in puncto .x. a quo cum ductae fue-
rinc .x.a.d. et .x.o.f. per centra dictorum circulorum, ipse erunt inuicem aequales, eo quod
cum .b.K. aequalis sit .q.p. igitur .x.d. et .q.p. erunt inuicem aequales, sed .f.x. aequalis est
q.p. quare .x.f. aequalis erit .x.d. tunc si .x. centrum fuerit unius circuli, cuius semidia-
mer sit una dictarum, problema solutum erit.
Talis etiam soiutio commo-
da erit ad inueniendum dictum
[Figure 305]
dato tamen quod eius diameter, ma
ior sit .b.z. cum in nostra potesta
te sit accipere puncta .K. et .p. pro
xima vel remota ab ipso .z. ad li-
bitum. Unde absque ulla divisio
neipsius .q.b. per medium, satis
erit signare puncta .K. et .p. dua-
bus distantiis mediantibus .b.K.
et .q.p. inuicem aequalibus, &
etiam propositis.
[Handwritten]

