Qualiter circulus designari possit alios duos circulos
propositos includens.
CLARISS. PETRO PIZZAMANO.
SUperioribus diebus per tuas literas a me quaesivisti, ut modum tibi scribere vel-
lem, quo circulus designari possit circunscribens alios duos propositos circulos.
Qua in re ut tibi satisfaciam quod maxime cupio ita rem accipe.
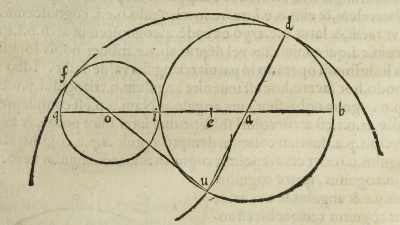
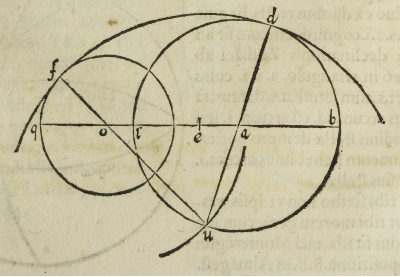
Propositi circuli sint, aut inter se contigui, aut intersecantes vel separati. Esto pri-
mũ contiguos esse, qui sint .d.b. et .f.q. quorum .d.b. maior sit et .f.q. minor, eorum vero
centra sint .a et .o. punctum autem contingentiae sit .i. nunc protrahatur. b.a.o.q. per centra eo
rum ab una circunferentia ad aliam, quae quidem linea transibit per punctum .i. ex
11, tertii Eucli. deinde a diametro maiori abscindatur .i.e. ad aequalitatem minoris
semidiametri, quo facto sumatur distantia inter .e. et .b. circino mediante factoque cen
tro .o. scindatur, alio circini pede, circunferentia maioris circuli in puncto .u. a quo si
mente concipiemus duas lineas .u.a.d. et .u.o.f. transeuntes per eorum centra .a. et .o.
usque ad circunferentias in punctis .d. et .f. ipsae erunt inuicem aequales, eo quod .e.i. sũ-
pta fuit aequalis .o.f. et .o.u. aequalis .e.b. quare .u.f. aequalis erit .b.i. sed u.d. etiam aequa
lis .b.i. ergo .u.d. aequalis erit u.f. & circulus, cuius u.d. vel .u.f. erit semidiameter, con-
tiguus erit ipsis propositis circulis ex conuerso .11. iam dictae. Idem dico pro circu-
lis se inuicem secantibus.
[Figure 302]
[Figure 303]

