Facsimile of Benedetti's Chapter on Mechanics
Image Transcription
Transcription
Decognitione latitudinum stellarum.
AD EUNDEM.
AD cognoscendam latitudinem stellae, eiusque declinationem, Monteregius in
10. propositione .8. li. Almagesti methodum satis docuit, sed si alia aliqua metho
do hoc idem cognoscere voluerimus, oportebit nos prius altitudinem poli cogno-
scere, deinde altitudinem meridianam ipsius stellae, nec non horam, quando ipsa stel
la in meridiano supra terram reperitur, qua hora mediante, illico cognoscemus pun
ctum ecclipticaea meridiano intersecto, eo tempore, quo stella coelum mediat su-
pra terram. Et quia ex cognita altitudine poli, illico cognoscitur altitudo aequa-
toris, cuius altitudinis differentia ab altitudine stellae est declinatio ipsius stellae, ha-
bebimus ideo eius declinationem cognitam; qua mediante ad cognoscendum etiam
latitudinem ita faciemus.
10. propositione .8. li. Almagesti methodum satis docuit, sed si alia aliqua metho
do hoc idem cognoscere voluerimus, oportebit nos prius altitudinem poli cogno-
scere, deinde altitudinem meridianam ipsius stellae, nec non horam, quando ipsa stel
la in meridiano supra terram reperitur, qua hora mediante, illico cognoscemus pun
ctum ecclipticaea meridiano intersecto, eo tempore, quo stella coelum mediat su-
pra terram. Et quia ex cognita altitudine poli, illico cognoscitur altitudo aequa-
toris, cuius altitudinis differentia ab altitudine stellae est declinatio ipsius stellae, ha-
bebimus ideo eius declinationem cognitam; qua mediante ad cognoscendum etiam
latitudinem ita faciemus.
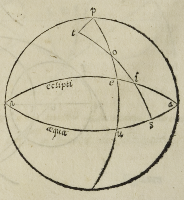
Sit exempli gratia .p.o.u. meridianus .u.a. vero aequator .e.a. autem eccliptica, &
o. centrum astri .u.o. vero eius declinatio ab aequatore, et .e.a. arcus aecclipticae inter
aequatorem, & meridianum, hoc est minor quarta, et .a.u. ascensio recta ipsius arcus,
et .u.e. sit declinatio puncti .e. aecclipticae ab aequatore, residuum vero declinationis stel-
lae sit .o.e. quae omnia nobis cognita erunt, sitque; .t. polus aecclipticus, a quo per .o. usque ad
aecclipticam transeat quarta .t.i. in qua quaerendus erit arcus .o.i. hoc modo.
o. centrum astri .u.o. vero eius declinatio ab aequatore, et .e.a. arcus aecclipticae inter
aequatorem, & meridianum, hoc est minor quarta, et .a.u. ascensio recta ipsius arcus,
et .u.e. sit declinatio puncti .e. aecclipticae ab aequatore, residuum vero declinationis stel-
lae sit .o.e. quae omnia nobis cognita erunt, sitque; .t. polus aecclipticus, a quo per .o. usque ad
aecclipticam transeat quarta .t.i. in qua quaerendus erit arcus .o.i. hoc modo.
Primum arcus .o.u: e.u: e.o: a.e: et .a.u. nobis cogniti sunt, cum angulo .a. declinatio
nis aeclipticae, & cum angulo .u. recto, unde ex .4. primi Copernici, cognoscemus angu
lum .a.e.u. collateralem, & eius .o.e.i. quare in triangulo .o.e.i. cognoscemus angulum
e. et deinde .i. ut rectum, & latus .o.e. ergo ex eadem .4. cognoscemus arcum .o.i. quaesitum,
& similiter arcum .e.i. qui coniunctus vel demptus ab .a.e. tribuet nobis longitudinem
stellae, sed quia huiusmodi operatio in paruis triangulis valde fallit. Ideo tibi sua-
deo alia methodo, hoc facere, hoc est inuenire angulum .o. trianguli .t.p.o. cuius duo
latera .t.p. et .p.o. cognita nobis sunt, cum angulo .p. Nam .o.p. est complementum de
clinationis stellae, et .p.t. est arcus coluri solstitiorum inter duos polos, & angulus .p.
residuum ex recto .t.p.a. duorum colurum dempto angulo. a, p.u. cognito ascensionis
recte, unde angulus .u.o.s. ut contrapositus cognitus remanet. angulus vero .u. rectus
est, & arcus .o.u. cognitus, quare cognitus
nobis erit arcus .u.s. & angulus .u.s.o. unde
arcus .a.s. nobis cognitus remanebit cum an-
gulo .a.s.i. residuo ex duobus rectis. Et quia
etiam angulus .s.a.i. cognitus est, cum sit an
gulus maximae declinationis Zodiaci ab
aequatore. Ideo in triangulo .a.s.i. cuius
duo anguli .a. et .s. cum latere .a.s. dantur, fa
cile inueniemus arcum .s.i. cum arcu .a.i. sed
a.i. erit longitudinis stellae dempto postea .
s.i. ex .s.o. iam inuento habebimus arcum .i.
o. latitudinis ipsius stellae.
nis aeclipticae, & cum angulo .u. recto, unde ex .4. primi Copernici, cognoscemus angu
lum .a.e.u. collateralem, & eius .o.e.i. quare in triangulo .o.e.i. cognoscemus angulum
e. et deinde .i. ut rectum, & latus .o.e. ergo ex eadem .4. cognoscemus arcum .o.i. quaesitum,
& similiter arcum .e.i. qui coniunctus vel demptus ab .a.e. tribuet nobis longitudinem
stellae, sed quia huiusmodi operatio in paruis triangulis valde fallit. Ideo tibi sua-
deo alia methodo, hoc facere, hoc est inuenire angulum .o. trianguli .t.p.o. cuius duo
latera .t.p. et .p.o. cognita nobis sunt, cum angulo .p. Nam .o.p. est complementum de
clinationis stellae, et .p.t. est arcus coluri solstitiorum inter duos polos, & angulus .p.
residuum ex recto .t.p.a. duorum colurum dempto angulo. a, p.u. cognito ascensionis
recte, unde angulus .u.o.s. ut contrapositus cognitus remanet. angulus vero .u. rectus
est, & arcus .o.u. cognitus, quare cognitus
nobis erit arcus .u.s. & angulus .u.s.o. unde
arcus .a.s. nobis cognitus remanebit cum an-
gulo .a.s.i. residuo ex duobus rectis. Et quia
etiam angulus .s.a.i. cognitus est, cum sit an
gulus maximae declinationis Zodiaci ab
aequatore. Ideo in triangulo .a.s.i. cuius
duo anguli .a. et .s. cum latere .a.s. dantur, fa
cile inueniemus arcum .s.i. cum arcu .a.i. sed
a.i. erit longitudinis stellae dempto postea .
s.i. ex .s.o. iam inuento habebimus arcum .i.
o. latitudinis ipsius stellae.
Haec autem tibi scribo non ut ipsis uta-
ris, sed potius ut tibi morem geram, cum bre
vissima methodus sit illa, quam Monteregius
scripsit in .10. propositione .8. li. in Almagest.
ris, sed potius ut tibi morem geram, cum bre
vissima methodus sit illa, quam Monteregius
scripsit in .10. propositione .8. li. in Almagest.