Facsimile of Benedetti's Chapter on Mechanics
Image Transcription
Transcription
terius differentiae quam supra inuenerimus.
Superius enim dixinon esse ponendum polum in .B. eo quod .B.C. sit gra .89. mi .
30. unde nobis prodiisset triangulus .f.C.D. trium valde paruorum laterum, quorum
latus .C.D. esset gra .o. mi .30. & latus .f.l. gra .o. mi .55. & latus .F.D. gra .o. mi .47. un-
de angulus .f. gra .32. min .40. falsus esset, qui quidem postea nobis daret .D.E. gra .45
minu .16. falsum similiter.
30. unde nobis prodiisset triangulus .f.C.D. trium valde paruorum laterum, quorum
latus .C.D. esset gra .o. mi .30. & latus .f.l. gra .o. mi .55. & latus .F.D. gra .o. mi .47. un-
de angulus .f. gra .32. min .40. falsus esset, qui quidem postea nobis daret .D.E. gra .45
minu .16. falsum similiter.
De passione circuli bactenus incognita.
AD EUNDEM.
DUbitandum quidem non est quin passiones circuli innumerabiles pene sint, quae
quidem omnes fere casu inueniuntur, ut mihi nunc accidit, quam tibi mitto,
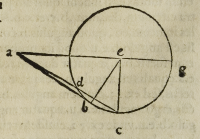
haec autem est, quod quadratum lineae .a.g. in figura hic subscripta semper aequale
est ei producto, quod fit ex .a.e. in diametro circuli .g.c.b. simul sumpto cum quadra
to inscriptibili in dicto circulo, & simul cum quadrato lineae .a.b. contingentis ipsum
circulum, supponendo .a.g. per centrum ipsius circuli transire.
quidem omnes fere casu inueniuntur, ut mihi nunc accidit, quam tibi mitto,
haec autem est, quod quadratum lineae .a.g. in figura hic subscripta semper aequale
est ei producto, quod fit ex .a.e. in diametro circuli .g.c.b. simul sumpto cum quadra
to inscriptibili in dicto circulo, & simul cum quadrato lineae .a.b. contingentis ipsum
circulum, supponendo .a.g. per centrum ipsius circuli transire.
Pro cuius demonstratione a centro .e. duco semidiametrum .e.c. perpendicularem
ipsi .g.a. & a puncto .c. ad .a. duco .c.a. quae secabit circunferentiam ipsius circuli in pum
cto .d. eo, quod angulus .c. acutus est. Nunc ex .35. tertii, productum .c.a. in .a.d. aequa
le est quadrato .a.b. productum autem .a.c. in .d.c. aequale est quadrato inscriptibili in
circulo .g.c.b. ex .130. primi Vitellionis, in qua propositione ipse Vitellio supplet pro
eo, quod in quinta propositione libri de lineis spirabilibus Archimedis desideratur,
sed quadratum .a.c. aequale est iis duobus productis. per .2. secundi Eucli. ergo qua-
dratum .a.c. aequale erit quadrato inscriptibili in circulo .d.c.g. & quadrato .a.b. sed
quadratum lineae .a.c. aequale est duobus quadratis, hoc est lineae .a.e. & lineae .e.c. ex
pitagorica, quare ex communi conceptu duo quadrata lineae .a.e. & lineae .e.c. hoc est
lineae .e.g. quod idem est, aequalia erunt duobus iam dictis, hoc est inscriptibili,
& ei, quod fit ex .a.b. sed quadratum lineae .a.g. aequale est quadrato lineae .a.e. & qua
drato quod fit ex .e.g. & duplo illius quod fit ex .a.e. in .e.g. hoc est producto .a.e. in
diametrum. Quare quadratum lineae .a.g. aequale est quadrato circunscriptibili, &
quadrato lineae .a.b. & producto lineae .a.e. in diametrum circuli .d.c.g.
ipsi .g.a. & a puncto .c. ad .a. duco .c.a. quae secabit circunferentiam ipsius circuli in pum
cto .d. eo, quod angulus .c. acutus est. Nunc ex .35. tertii, productum .c.a. in .a.d. aequa
le est quadrato .a.b. productum autem .a.c. in .d.c. aequale est quadrato inscriptibili in
circulo .g.c.b. ex .130. primi Vitellionis, in qua propositione ipse Vitellio supplet pro
eo, quod in quinta propositione libri de lineis spirabilibus Archimedis desideratur,
sed quadratum .a.c. aequale est iis duobus productis. per .2. secundi Eucli. ergo qua-
dratum .a.c. aequale erit quadrato inscriptibili in circulo .d.c.g. & quadrato .a.b. sed
quadratum lineae .a.c. aequale est duobus quadratis, hoc est lineae .a.e. & lineae .e.c. ex
pitagorica, quare ex communi conceptu duo quadrata lineae .a.e. & lineae .e.c. hoc est
lineae .e.g. quod idem est, aequalia erunt duobus iam dictis, hoc est inscriptibili,
& ei, quod fit ex .a.b. sed quadratum lineae .a.g. aequale est quadrato lineae .a.e. & qua
drato quod fit ex .e.g. & duplo illius quod fit ex .a.e. in .e.g. hoc est producto .a.e. in
diametrum. Quare quadratum lineae .a.g. aequale est quadrato circunscriptibili, &
quadrato lineae .a.b. & producto lineae .a.e. in diametrum circuli .d.c.g.
Breviori etiam methodo demonstrare possu
mus quadrata lineae .a.e. et .e.g. aequalia es-
se quadrato circunscriptibili, & quadrato lineae .
a.b. ducendo lineam .e.b. quae aequalis est lineae .
e.g. tali methodo, hoc est, considerando, quod
quadratum inscriptibile semper duplum est qua
drato semidiametri, vel medietati circumscri-
ptibili, quod quidem nihil aliud est, nisi aequale
esse iis duobus quadratis, hoc est lineae .e.b. & li-
neae .e.g. sed quadratum lineae .a.e. aequale est iis
duobus quadratis, hoc est lineae .a.b. & lineae .b.e. unde quadrat um lineae .a.e. cum
quadrato lineae .e.g. aequale est quadrato circunscriptibili, simul collecto cum qua-
drato lineae .a.b.
mus quadrata lineae .a.e. et .e.g. aequalia es-
se quadrato circunscriptibili, & quadrato lineae .
a.b. ducendo lineam .e.b. quae aequalis est lineae .
e.g. tali methodo, hoc est, considerando, quod
quadratum inscriptibile semper duplum est qua
drato semidiametri, vel medietati circumscri-
ptibili, quod quidem nihil aliud est, nisi aequale
esse iis duobus quadratis, hoc est lineae .e.b. & li-
neae .e.g. sed quadratum lineae .a.e. aequale est iis
duobus quadratis, hoc est lineae .a.b. & lineae .b.e. unde quadrat um lineae .a.e. cum
quadrato lineae .e.g. aequale est quadrato circunscriptibili, simul collecto cum qua-
drato lineae .a.b.