Facsimile of Benedetti's Chapter on Mechanics
Image Transcription
Transcription
praecise idest intervallum inter centrum mundi, & centrum epicycli Martis in huius-
modi situ.
modi situ.
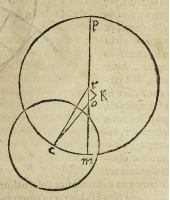
Fingemus igitur eccenticum Martis significatum per .p.c.m. cuius centrum sit .r.
& lineam augis .p.r.o.m. in qua centrum mundi sit .o. centrum autem verum epicycli,
comprehendatur ab angulo .p.o.c. qui sit graduum .151. min .30. secundum supposi-
tum. Quare in puncto .c. erit centrum epicycli. Imaginemur ergo .c.o. productam a
parte .o. quousque ab .r. centro deferentis veniat linea .r.k. perpendiculariter, faciens
angulum rectum in puncto. k & quoniam angulus .r.o.c. datur nobis graduum .151.
min .30. ideo cognoscemus angulum .r.o.k. tanquam reliquum ex duobus rectis, qui
erit gra .28. min .30. & similiter angu-
lum .o.r.k. tanquam residuum unius
recti, qui erit gra .61. min .30. cuius si-
nus idest .o.k. erit partium .8788 1. et .k.
r. ut sinus anguli .r.o.k. partium .47715
talium qualium .o.r. esset 100000. sed
ut .o.r. est .6. latus .o.k. erit .5. & min .16
et .r.k. partium .2. min .52. & quia .r.c.
cst partium 60. eiusmodi, si ab eius qua-
drato subtractum fuerit quadratum ip
sius .r.k. reliquum erit nobis quadratum
ipsius .k.c. cuius radix, idest .k. erit par-
tium .59. min .56. a qua .c.k. subtrahen-
do postea .k.o. partium .5. minu .16. re-
manebit .o.c. partium .54. min .40. pro
distantia quaesita.
& lineam augis .p.r.o.m. in qua centrum mundi sit .o. centrum autem verum epicycli,
comprehendatur ab angulo .p.o.c. qui sit graduum .151. min .30. secundum supposi-
tum. Quare in puncto .c. erit centrum epicycli. Imaginemur ergo .c.o. productam a
parte .o. quousque ab .r. centro deferentis veniat linea .r.k. perpendiculariter, faciens
angulum rectum in puncto. k & quoniam angulus .r.o.c. datur nobis graduum .151.
min .30. ideo cognoscemus angulum .r.o.k. tanquam reliquum ex duobus rectis, qui
erit gra .28. min .30. & similiter angu-
lum .o.r.k. tanquam residuum unius
recti, qui erit gra .61. min .30. cuius si-
nus idest .o.k. erit partium .8788 1. et .k.
r. ut sinus anguli .r.o.k. partium .47715
talium qualium .o.r. esset 100000. sed
ut .o.r. est .6. latus .o.k. erit .5. & min .16
et .r.k. partium .2. min .52. & quia .r.c.
cst partium 60. eiusmodi, si ab eius qua-
drato subtractum fuerit quadratum ip
sius .r.k. reliquum erit nobis quadratum
ipsius .k.c. cuius radix, idest .k. erit par-
tium .59. min .56. a qua .c.k. subtrahen-
do postea .k.o. partium .5. minu .16. re-
manebit .o.c. partium .54. min .40. pro
distantia quaesita.
Fingamus postea epicyclum .f.n.g.
in quo argumentum verum graduum .
149. minu .39. sit arcus .f.n. ubi Mars inueniatur in .n. per quem punctum transeat li-
nea .o.n. veri motus Martis. Deinde inueniamus angulum .c.o.n. aequationis argumem
ti, modo iam dicto, idest ducendo sinum .n.h. arcus .n.g. qui arcus tanquam reliquus
argumenti veri, iam praesuppositi, ex dimidio circulo, erit graduum 30. minu .21. &
n.h. eius sinus partium .50528. sinus similiter anguli .n.c.h. et .c.h. tanquam sinus an-
guli .c.n.h. restantis ex uno recto grad .59. minu .39. erit partium .86295. talium qua-
lium .c.n. sinus totus esset partium .100000. sed ut partium .39. & min .30. sinus .c.h.
erit partium .34. min .5. et .n.h. partium .19. mi .57. reliquum postea .h.o. ex .o.c. par-
tium .20. min .35. quia iam supra inuenimus .o.c. esse partium eiusmodi .54. minu .40.
unde .o.n. ut radix quadrata summae duorum .n.h. et .h.o. erit partium .28. minu .41.
talium qualium .n.h. inuenta fuit partium .19. min .57. quae .n.h. erit postea partium,
69552. talium qualium .n.o. partium .100000. & sumpta dicta .n.h. ut sinus dictarum
partium, dabit nobis angulum .n.o.h. quaesitum gra .44. min .4. qui per tabulas Alfon
si inuentus est gra .44. min .2. par huic, ut dici potest. Quiangulus gra .44. minu .4.
collectus cum angulo veri centri iam supposito graduum .151. minu .20. & cum an-
gulo augis eccentrici Martis, similiter suppositae grad .135. min .5. dabit nobis sum-
mam verae distantiae Martis a principio Arietis grad .330. min .29. quod aliud non
significat, nisi quod Mars inuenietur in minu .29. primi gradus Piscium. Et Stofle-
rus in suis ephemeridibus ponit eum in .22. minuto dicti primi gradus, cuius diffe-
in quo argumentum verum graduum .
149. minu .39. sit arcus .f.n. ubi Mars inueniatur in .n. per quem punctum transeat li-
nea .o.n. veri motus Martis. Deinde inueniamus angulum .c.o.n. aequationis argumem
ti, modo iam dicto, idest ducendo sinum .n.h. arcus .n.g. qui arcus tanquam reliquus
argumenti veri, iam praesuppositi, ex dimidio circulo, erit graduum 30. minu .21. &
n.h. eius sinus partium .50528. sinus similiter anguli .n.c.h. et .c.h. tanquam sinus an-
guli .c.n.h. restantis ex uno recto grad .59. minu .39. erit partium .86295. talium qua-
lium .c.n. sinus totus esset partium .100000. sed ut partium .39. & min .30. sinus .c.h.
erit partium .34. min .5. et .n.h. partium .19. mi .57. reliquum postea .h.o. ex .o.c. par-
tium .20. min .35. quia iam supra inuenimus .o.c. esse partium eiusmodi .54. minu .40.
unde .o.n. ut radix quadrata summae duorum .n.h. et .h.o. erit partium .28. minu .41.
talium qualium .n.h. inuenta fuit partium .19. min .57. quae .n.h. erit postea partium,
69552. talium qualium .n.o. partium .100000. & sumpta dicta .n.h. ut sinus dictarum
partium, dabit nobis angulum .n.o.h. quaesitum gra .44. min .4. qui per tabulas Alfon
si inuentus est gra .44. min .2. par huic, ut dici potest. Quiangulus gra .44. minu .4.
collectus cum angulo veri centri iam supposito graduum .151. minu .20. & cum an-
gulo augis eccentrici Martis, similiter suppositae grad .135. min .5. dabit nobis sum-
mam verae distantiae Martis a principio Arietis grad .330. min .29. quod aliud non
significat, nisi quod Mars inuenietur in minu .29. primi gradus Piscium. Et Stofle-
rus in suis ephemeridibus ponit eum in .22. minuto dicti primi gradus, cuius diffe-