In the years 1925 to 1927, the old quantum theory was replaced by the newly developed theory of quantum mechanics, which grew out of the matrix mechanics of Heisenberg, Born, and Jordan and the wave mechanics of Schrödinger. Both of these theories were initially formulated entirely non-relativistically. But it was clear from the outset that contact would have to be made with the special theory of relativity for two important reasons: On the one hand, the mechanics would have to be complemented with a quantum electrodynamics (QED), in order to describe the emission and absorption of radiation, as well as the particulate properties of light itself, which by this time (in the wake of the discovery and interpretation of the Compton effect) was a generally accepted fact. On the other hand, the mechanics itself would have to be made relativistic, as it was known, already since the mid 1910s, that relativistic corrections to the kinematics of the electron would have a measurable effect in the fine structure of atomic spectra.
It was Schrödinger’s wave mechanics, rather than matrix mechanics, that provided the ideal starting point for a relativistic kinematics of matter: One needed to find a new, relativistic matter wave equation, but at first glance there were no immediate other conceptual difficulties, such as the problem of a non-commuting time variable in matrix mechanics. Schrödinger himself had initially attempted to find a relativistic wave equation, following de Broglie’s program of matter waves, which had been formulated in a relativistic manner. But de Broglie had stopped short of addressing the dynamical equations. Schrödinger in fact arrived at the Klein Gordon equation, but he dismissed it, due to its empirical inadequacy (later understood as the absence of spin in the Klein Gordon equation). Others were not as scrupulous, and the Klein Gordon equation was rediscovered (and published) multiple times in the immediate aftermath of Schrödinger’s first papers on wave mechanics.1
Which role did general relativity play in this context? In full analogy with the case of special relativity, two distinct problems can be distinguished. On the one hand, there is the question of a quantum theory of the gravitational field. This will be discussed in the next part. On the other hand, there is the question of how quantum matter interacts with a gravitational field. We will be discussing this aspect first, because it is primary both logically and historically: Many of those who attempted a relativistic generalization of Schrödinger’s program didn’t see a reason to stop at special relativity—after all, the final quantum wave equation should also be compatible with general relativity and be able to describe the interaction of microscopic matter with a gravitational field. In two cases, the re-discovery of the Klein Gordon equation thus actually occurred in the context of curved space-time, in the work of Théophile de Donder and Oskar Klein.
It should be noted that at the time, quantum mechanics was far from being well enough established for these works to be viewed as merely an application of the new quantum theory to general relativity. Rather, by incorporating wave mechanics within the better-established framework of general relativity, they sought to put the former on a surer foundation. From a modern viewpoint, De Donder’s papers are notable for delivering the first construction of a Klein Gordon equation in curved spacetime (Chapter 7). But for de Donder this was not the central point. Rather, the generalization of Schrödingers “quantization” procedure for arriving at the Schrödinger equation to the generally relativistic case was in some sense meant to motivate the quantization procedure itself, even if de Donder’s reasoning on this point is rather sketchy (Chapter 6).
In a similar vein, Klein’s attempt to bring together wave mechanics with the five-dimensional extension of GR, proposed by Kaluza (1921) in order to unify gravity and electromagnetism, might simply be read as the construction of a Klein Gordon wave equation in curved spacetime with an electromagnetic potential. But Klein’s main ambition was to see whether the interpretation of Schrödinger’s waves as waves in actual spacetime, which the likes of Bohr and Heisenberg doubted from the very start, might in fact be saved in a five-dimensional spacetime (Chapter 8). These hopes, cautiously voiced by Klein in the conclusion to his paper, were soon to be dashed, when Klein realized that such a theory would never be able to explain Planck’s law of black body radiation, the problem that had led to quantum theory in the first place. In 1927, Klein converted to the probabilistic camp, now placing his hopes for a spatio-temporal description in the newly emerging quantum field theory.
This did not immediately change Klein’s research program: He continued to elaborate his classical five-dimensional field theory, but now viewed it merely as a starting point for quantization. While work on a full theory of quantum electrodynamics was well underway at this time, the quantization of gravity was not viewed as an immediate concern. Klein’s second paper (Chapter 9) thus begins with some remarks on why general relativity would need to be modified according to the postulates of quantum theory. This is the first published argument for the necessity of quantizing the gravitational field. He further argued that gravity and electrodynamics should be quantized simultaneously, that is, that one should quantize a unified field theory rather than simple Maxwellian electrodynamics (interacting with a Klein Gordon matter field), as this would, in particular, allow for a unification of the conservation laws of energy-momentum and of charge.
Indeed, if Klein’s later recollections are to be believed, his five-dimensional field theory initially formed the classical basis for Heisenberg’s and Pauli’s attempts at formulating QED.2 That is, until the Dirac equation came along in 1928 and ousted the Klein Gordon equation as the best description of relativistic quantum matter. Initially, Dirac saw one main advantage in his new equation over the old Klein Gordon one, namely that it could be interpreted as a one-particle, quantum mechanical Schrödinger equation (Dirac 1928). But even those who believed that any theory of matter waves would necessarily have to be second-quantized immediately realized the superiority of the Dirac equation, incorporating as it did the spin of the electron (and the proton).
In the wake of the Dirac equation, work immediately began on its integration into general relativity, the most immediate goal being the formulation of the Dirac equation in a curved (but non-dynamical) space-time. The first step in this direction was taken by Hugo Tetrode, already in 1928 (Chapter 10). The general idea was the following: In Dirac’s derivation, the flat Minkowski space-time metric
 shows up in the algebra of the Dirac
shows up in the algebra of the Dirac
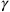 matrices:
matrices:
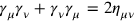
|
5.1 |
Tetrode’s starting point was now to replace the Minkowski metric in this relation with a generalized non-flat metric
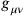 , turning the (elements of the)
, turning the (elements of the)
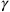 matrices from constants into space-time dependent quantities, determined by the value of the metric at a given space-time point. But this determination was not unique, in fact it did not even offer a clear prescription for constructing the
matrices from constants into space-time dependent quantities, determined by the value of the metric at a given space-time point. But this determination was not unique, in fact it did not even offer a clear prescription for constructing the
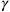 matrices when the metric was given. Tetrode only presented some tentative attempts at finding such a prescription, but, soon after, Eugene Wigner proposed that one could answer this question by making use of a formalism that Einstein had developed in that same year (1928), but in an entirely different context (Wigner 1929).
matrices when the metric was given. Tetrode only presented some tentative attempts at finding such a prescription, but, soon after, Eugene Wigner proposed that one could answer this question by making use of a formalism that Einstein had developed in that same year (1928), but in an entirely different context (Wigner 1929).
Einstein’s idea was to replace the metric
 as the fundamental quantity of his general theory of relativity with so-called “vierbeine” (tetrads), that is, for each point in spacetime a local coordinate system spanned by four orthonormal basis vectors
as the fundamental quantity of his general theory of relativity with so-called “vierbeine” (tetrads), that is, for each point in spacetime a local coordinate system spanned by four orthonormal basis vectors
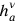 , with
, with
 running from one to four (Einstein 1928). The metric at a given point was determined by the tetrad to be
running from one to four (Einstein 1928). The metric at a given point was determined by the tetrad to be

|
5.2 |
but the metric by itself did not determine the tetrads. Indeed, the metric is unchanged by an arbitrary local Lorentz transformation of the tetrads
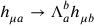
|
5.3 |
Einstein now proposed that the relative orientation of the tetrads was not redundant information, but actually carried physical meaning. In other words, once one has defined an
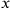 axis at some point in spacetime, it makes a difference what I call
axis at some point in spacetime, it makes a difference what I call
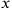 axis in some other point—the only allowed transformations are then global Lorentz transformations, which conserve the relative orientation of the tetrads. This allowed one to speak of vectors at different spacetime points as parallel if they had the same components with regard to their local tetrad; hence Einstein’s theory went by the name of teleparallelism. Through the notion of teleparallelism, the tetrads thus defined a second connection (beside the usual Levi-Civita connection one could obtain from the metric tensor alone) which could be used to construct new tensors and invariants, which could in turn be used to write down more general field equations. Einstein believed that he could thereby construct combined field equations for the gravitational and electromagnetic fields.
axis in some other point—the only allowed transformations are then global Lorentz transformations, which conserve the relative orientation of the tetrads. This allowed one to speak of vectors at different spacetime points as parallel if they had the same components with regard to their local tetrad; hence Einstein’s theory went by the name of teleparallelism. Through the notion of teleparallelism, the tetrads thus defined a second connection (beside the usual Levi-Civita connection one could obtain from the metric tensor alone) which could be used to construct new tensors and invariants, which could in turn be used to write down more general field equations. Einstein believed that he could thereby construct combined field equations for the gravitational and electromagnetic fields.
Wigner realized that, independent of these unified field theory considerations,3 given local tetrads one could give a unique prescription for the construction of the
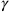 matrices in curved spacetime as
matrices in curved spacetime as
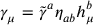
|
5.4 |
where the
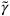 are the usual (constant) Dirac matrices; the Dirac matrices on curved spacetime
are the usual (constant) Dirac matrices; the Dirac matrices on curved spacetime
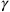 can then easily be shown to obey the correct anti-commutation relations. The open question was then: Given the Dirac matrices in curved spacetime, how were they to be incorporated into the Dirac equation? Both Tetrode and Wigner had tried this, but they had mainly concerned themselves with the question of how space-time dependent
can then easily be shown to obey the correct anti-commutation relations. The open question was then: Given the Dirac matrices in curved spacetime, how were they to be incorporated into the Dirac equation? Both Tetrode and Wigner had tried this, but they had mainly concerned themselves with the question of how space-time dependent
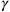 matrices were to be integrated into the Dirac equation, which of course contained derivatives with respect to space and time. The general covariance of the wave equations they ended up with was, however, very questionable. This question was soon taken up by Vladimir Fock, initially in collaboration with Dimitri Ivanenko.
matrices were to be integrated into the Dirac equation, which of course contained derivatives with respect to space and time. The general covariance of the wave equations they ended up with was, however, very questionable. This question was soon taken up by Vladimir Fock, initially in collaboration with Dimitri Ivanenko.
Fock’s main innovation was introducing the notion of the covariant derivative of a spinor, which allowed for a manifestly covariant Dirac equation in curved spacetime (Chapter 11). The connection appearing in the covariant spinor derivative was determined by the Dirac matrices in curved spacetime, which in turn were determined by the tetrads. But Fock could show that his Dirac equation was indeed covariant under local Lorentz transformations, that is, that the choice of tetrads (beyond what was determined by the metric) played no physical role. The tetrads were thus demoted to mere mathematical tools, in contrast with the physical role they had played in Einstein’s teleparallelism.
A very similar approach was developed independently by Hermann Weyl (Chapter 12).4 But Weyl’s approach differed fundamentally from Fock’s in its perceived goal. Fock came from quantum theory and viewed his work as an extension of Dirac’s theory to the case of curved spacetime. Weyl, on the other hand, is a representative of the viewpoint, which we already encountered in the work of de Donder and the early Klein, that general relativity might help in solving foundational issues in quantum mechanics. For while the original problems of motivating the quantization procedure or interpreting the wave function had largely been set aside by 1929 (the year of Weyl’s and Fock’s work), the Dirac equation brought with it new fundamental difficulties, most notably the problem of the negative energy states.
Weyl attempted to solve this difficulty by replacing the four-spinors of Dirac with the two-spinors that now carry Weyl’s name. This removed the negative energy solutions, but at the same time also prevented the inclusion of the usual explicit mass term in the wave equation. Weyl expressed the rather vague hope that the mass might arise through the coupling to a gravitational field and, to this end, constructed an essentially classical field theory of coupled spinor, gravitational and electromagnetic fields, which, just like Klein’s five-dimensional field theory two years earlier, was eventually supposed to be quantized. In order to couple the spinors to the gravitational field, he introduced the same tetrad-based covariant spinor derivative that Fock had constructed. For the coupling of the spinors to the electromagnetic field, he discovered, almost in passing, the local gauge invariance of the Dirac equation, which he not only related to, but in fact tried to deduce from local Lorentz invariance.
The work of Weyl and Fock was received in two distinct ways: Some, coming to the problem from general relativity, attempted to further pursue the solution of the negative energy problem along these lines, most notably Jan Schouten, who attempted to show how a mass term for Weyl spinors might arise in five- instead of four-dimensional curved spacetime (Schouten 1931). In the quantum community, on the other hand, the work of Weyl and Fock was viewed as the classical basis for a relativistic quantum field theory of gravitation, electromagnetism and charged Dirac particles, and an attempt to quantize it was undertaken almost immediately by Léon Rosenfeld (see the following part of this book). It was important for this undertaking that Weyl and Fock had not only shown how to couple spinor waves to a gravitational field, but had also identified the degrees of freedom in general relativity that were supposed to be subjected to quantization in such a coupled theory, the tetrads.
In 1932, Schrödinger showed that this was not the unique way of integrating spinors into general relativity. He took the spacetime dependent Dirac matrices as fundamental degrees of freedom, instead of the tetrads (Chapter 13). This brought the question of which basis to choose for the Dirac matrices back onto the table: In the tetrad prescription, equation 5.4, one simply had to initially pick some basis for the constant Dirac matrices; everything else then followed from the tetrads and their transformation properties. But if the
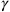 matrices themselves were supposed to be the dynamical variables, no direct reference could be made to the constant matrices. Schrödinger thus imposed further hermiticity conditions, which defined the space-time dependent Dirac matrices, given a metric, up to a unitary transformation in spin space. These unitary transformations were not only, as Schrödinger put it, “benign and irrelevant,” they also corresponded exactly to the local Lorentz transformations in the Weyl-Fock tetrad formalism. What had thus, using tetrads, looked like the rotation of local coordinate axes, in Schrödinger’s formalism was interpreted as a (local) transformation in spin space. This latter point, in particular, was soon after further worked out by Bargmann (1932) and Pauli (1933).
matrices themselves were supposed to be the dynamical variables, no direct reference could be made to the constant matrices. Schrödinger thus imposed further hermiticity conditions, which defined the space-time dependent Dirac matrices, given a metric, up to a unitary transformation in spin space. These unitary transformations were not only, as Schrödinger put it, “benign and irrelevant,” they also corresponded exactly to the local Lorentz transformations in the Weyl-Fock tetrad formalism. What had thus, using tetrads, looked like the rotation of local coordinate axes, in Schrödinger’s formalism was interpreted as a (local) transformation in spin space. This latter point, in particular, was soon after further worked out by Bargmann (1932) and Pauli (1933).
A further alternative was worked out by Bartel van der Waerden and Leopold Infeld (Chapter 14), based on a generalization of van der Waerden’s special relativistic spinor calculus (Waerden 1929).5 They defined, instead of the local coordinate basis of the tetrad formalism, local spinor spaces. The separation between local spin space transformations and coordinate transformations was thus now taken as the starting point, rather than as a result of the analysis. As in special relativistic spinor calculus, where vectors are constructed from spinors through the Pauli matrices, the connection between spinor space and spacetime was established through a set of local, spacetime dependent generalized Pauli matrices. These matrices replaced the metric as fundamental degrees of freedom. They were thus the two-spinor analog of Schrödinger’s spacetime dependent Dirac matrices. In a sense, Infeld/van der Waerden was to Schrödinger as Weyl was to Fock: The same general idea, but with two-spinors instead of four-spinors. Van der Waerden viewed his formalism as a considerable simplification of Schrödinger’s four-dimensional framework, since one no longer needed to employ hermiticity conditions in order to fix the dynamical matrix degrees of freedom.6
Both the Schrödinger and the Infeld-van der Waerden formalism had to wait quite a while until they were put to use. Even though Pauli immediately suggested to Rosenfeld that he should repeat his analysis of 1930, this time quantizing the Dirac matrices instead of tetrads,7 Schrödinger’s reformulation was, to the best of my knowledge, not used as the basis for a quantization of gravity until Bryce de Witt’s thesis work in the late 1940s. And, still in 1951,8 Schrödinger remarked to Fredrik Belinfante: “I do not set any store in my paper of 1932 on Dirac’s theory in a general metric. It was at the time a smart exercise, but it came to nothing.” Van der Waerden was equally dismissive of his work. His formalism had to wait even longer, until the late 1950s, before it was widely received, mainly, however, in the context of mathematical relativity, rather than as a basis for quantization.9
In any case, by the early 1930s it appeared that the classical field theory of relativistic quantum matter interacting with the gravitational field had been worked out, in several closely related mathematical formulations. The core difficulties were seen to lie in the quantization procedure, which, already for the simpler case of electrodynamic interactions, led to uninterpretable infinities in the higher orders of perturbation theory.
In 1938, however, a study by Einstein, Infeld, and Banesh Hoffmann (EIH) appeared, which appeared to indicate that there were serious advantages to starting with a classical theory of matter as point particles, in contradiction, ironically, with Einstein’s program of a unified field theory (Chapter 15). EIH could show that if one treated matter particles as singularities in the gravitational field , one could (in stepwise approximations) derive the equations of motion for these singularities from the field equations alone, without having to additionally postulate the geodesic equations for particle motion. The prospect of carrying this feature of general relativity over to the quantum theory made a classical theory of point particles (rather than a classical theory of matter waves to be second-quantized) an attractive starting point for a quantum theory of gravitation. This approach was taken by Peter Bergmann, as will be discussed in the final part of this book.
Several different possible starting points for a quantization of gravity, that is, a modification of general relativity according to the principles of quantum theory, had thus been set. But the inverse program, the modification of quantum theory following considerations from general relativity, was not dead. As we have seen, this program by the late 1920s mainly centered around the idea that the inclusion of general relativity might somehow determine the mass of the elementary particles, which were after all purely empirical parameters in the wave equations of quantum mechanics and field theory.
A variant of this idea, which brought in ideas from relativistic cosmology, had been formulated early on by Arthur Eddington (1923). He hypothesized that the radius of the electron (proportional to the inverse mass) should be related (in fact proportional) to the curvature radius
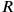 of the universe as a whole, still viewed at the time as static and spherical (an Einstein universe). Eddington further elaborated on this idea 13 years later in the context of his notorious and oft-ridiculed relativistic theory of protons and electrons (Eddington 1936),10 obtaining the necessarily huge proportionality constant through the square root of the number
of the universe as a whole, still viewed at the time as static and spherical (an Einstein universe). Eddington further elaborated on this idea 13 years later in the context of his notorious and oft-ridiculed relativistic theory of protons and electrons (Eddington 1936),10 obtaining the necessarily huge proportionality constant through the square root of the number
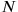 of electrons (or protons) in the entire universe.
of electrons (or protons) in the entire universe.
While this work was almost universally regarded as obscure and incomprehensible, some of the general ideas concerning the relation between cosmology and elementary particles were taken up by Erwin Schrödinger.11 Schrödinger saw some promise in Eddington’s new work, inasmuch as it was a specification of the original idea of connecting the electron mass with cosmology, now also incorporating the tools of wave mechanics. In particular, Eddington had derived the rest mass energy of an elementary particle as the energy of the first excited state for the system of all the identical fermions in the universe. The curvature radius of the universe entered through the boundary conditions for the wave equation, the total number of particles in the universe through the fact that one was looking at energies near the Fermi surface. In a stripped-down version, which Schrödinger presented at the Galvani Bicentennial in 1937 (Schrödinger 1938b) and which made no more reference to the more eccentric aspects of Eddington’s theory (such as the attempt to prove that the fine structure constant was necessarily the reciprocal of an integer),12 the central relation read:
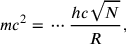
|
5.5 |
where the dots refer to undetermined constants. In order to obtain such a relation from the accepted wave mechanics, rather than from Eddington’s novel theory, Schrödinger devoted considerable energy to the explicit construction of the solutions of the Maxwell and Dirac equations in a spherical universe (Schrödinger 1938a), also studying the non-static, expanding case, which was by that time heavily favored (Schrödinger 1940). But after three years of working on this subject, he had to conclude in a small note that one would, starting from very general assumptions, always obtain the cubic root of
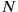 in Eddington’s relation, instead of the square root, and thus obtain much too small masses for the elementary particles (Chapter 16).
in Eddington’s relation, instead of the square root, and thus obtain much too small masses for the elementary particles (Chapter 16).
The idea that general relativity, in particular relativistic cosmology, might directly determine the microscopic quantum wave equations thus remained nothing more than a tantalizing possibility. In contrast, the program of quantizing the gravitational field, while technically challenging, seemed a fairly straightforward task. In this section, we have discussed the necessary groundwork for this task, that is, the establishment of classical theories of matter interacting with the gravitational field that went beyond the very unspecific energy-momentum tensor of matter appearing in the Einstein equations. In the next section, we will discuss the first attempts at an actual quantization of such theories.
References
Bargmann, Valentine (1932). “Bemerkungen Zur Allgemein-Relativistischen Fassung Der Quantentheorie.” Sitzungsberichte Der Preussischen Akademie Der Wissenschaften, 346–54.
Dirac, Paul A. M. (1928). “Zur Quantentheorie Des Elektrons.” In Quantentheorie Und Chemie, edited by Hans Falkenhagen, 85–94. Leipzig: S. Hirzel.
Eddington, Arthur S. (1923). The Mathematical Theory of Relativity. Cambridge: Cambridge University Press.
——— (1936). Relativity Theory of Protons and Electrons. London: Cambridge University Press.
Einstein, Albert (1928). “Riemann-Geometrie Mit Aufrechterhaltung Des Begriffes Des Fernparallelismus.” Sitzungsberichte Der Preussischen Akademie Der Wissenschaften, 217–21.
Goenner, Hubert F. M. (2004). “On the History of Unified Field Theories.” Living Reviews in Relativity 7 (2): 1–153.
Kaluza, Theodor (1921). “Zum Unitätsproblem Der Physik.” Sitzungsberichte Der Preussischen Akademie Der Wissenschaften, 966–72.
Kilmister, Clive W. (1994). Eddington’s Search for a Fundamental Theory: A Key to the Universe. Cambridge: Cambridge University Press.
Kragh, Helge (1984). “Equation with the Many Fathers: The Klein-Gordon Equation in 1926.” American Journal of Physics 52 (11): 1024–33.
——— (2015). “On Arthur Eddington’s Theory of Everything.” arXiv:1510.04046.
Meyenn, Karl von, ed. (1993). Wolfgang Pauli: Wissenschaftlicher Briefwechsel Mit Bohr, Einstein, Heisenberg U.a. Vols. Vol. 3: 1940–1949. Berlin: Springer.
Pauli, Wolfgang (1933). “Über Die Formulierung Der Naturgesetze Mit Fünf Homogenen Koordinaten. II. Die Diracschen Gleichungen Für Die Materiewellen.” Annalen Der Physik 5 (18): 337–72.
Penrose, Roger (1960). “A Spinor Approach to General Relativity.” Annals of Physics 10 (2): 171–201.
Schneider, Martina R. (2010). “Die Physikalischen Arbeiten Des Jungen B. L. van Der Waerden.” PhD thesis, Bergische Universität Wuppertal.
Scholz, Erhard (2005). “Local Spinor Structures in V. Fock’s and H. Weyl’s Work on the Dirac Equation (1929).” In Géométrie Au Vigntième Siècle, 1930–2000, edited by D. Flament, J. Kouneiher, P. Nabonnand, and J.-J. Szsceciniarz, 284–301. Paris: Hermann.
Schouten, Jan A. (1931). “Dirac Equations in General Relativity.” Journal of Mathematics and Physics 10: 239–83.
Schrödinger, Erwin (1938a). “Eigenschwingungen Des Sphärischen Raumes.” Commentationes Pontificiae Academiae Scientiarum 2: 321–64.
——— (1938b). “Sur La Théorie Du Monde d’Eddington.” Il Nuovo Cimento 15: 246–54.
——— (1940). “Maxwell’s and Dirac’s Equations in the Expanding Universe.” Proceedings of the Royal Irish Academy 46A: 25–47.
Urbantke, Helmuth (1992). “Schrödinger and Cosmology.” In Studies in the History of General Relativity, Einstein Studies Vol. 3, edited by Jean Eisenstaedt and A. J. Kox, 453–59. Boston: Birkhäuser.
Waerden, Bartel van der (1929). “Spinoranalyse.” Nachrichten von Der Gesellschaft Der Wissenschaften Zu Göttingen, Math.-Phys. Klasse, 100–109.
Wigner, Eugene P. (1929). “Eine Bemerkung Zu Einsteins Neuer Formulierung Des Allgemeinen Relativitätsprinzips.” Zeitschrift Für Physik 53 (7): 592–96.
Footnotes
Oral history interview conducted by J. L. Heilbron and L. Rosenfeld on 25 February 1963, Niels Bohr Library and Archives, American Institute of Physics, College Park, MD, USA, http://www.aip.org/history/ohilist/4709_3.html.
As we shall see, this is just one instance of the close connection between developments in unified field theory and the Dirac equation in curved space-time. For a detailed discussion from the viewpoint of the history of unified theory, see Goenner (2004).
For a detailed study of van der Waerden’s work in physics, including this paper, see Schneider (2010).
See the letter from van der Waerden to Schrödinger, 14 June 1932, Schrödinger papers, Vienna University Library.
Letter from Schrödinger to Belinfante, 16 March 1951, Archive for the History of Quantum Physics.
For more on this work in the context of Schrödinger’s work on cosmology more generally, see Urbantke (1992).
Still, reactions were mixed. On 18 February 1938, Sommerfeld wrote to Schrödinger: “It is wonderful that you are now seriously working on Eddingt.[on].” (Es ist wundervoll, dass Sie mit Eddingt.[on] Ernst machen) but also talked about Bohr’s “arrogant dismissal” (bonzenhafte Ablehnung), Schrödinger papers, Vienna University Library.
