In the years 1926–1928, immediately following the creation of matrix and wave mechanics, the protagonists of this development elaborated and expanded the techniques of the new quantum mechanics, so as to apply them to field theories.1 This work culminated in the theory of interacting quantum electrodynamics (QED),2 published in 1929 by Werner Heisenberg and Wolfgang Pauli (Heisenberg and Pauli 1929a). This paper, which deals mainly with the canonical quantization of both the electromagnetic and the matter-wave fields, famously contains a brief nod to gravitational theory, which is nowadays often quoted jokingly due to its seemingly naive optimism:
We further note that a quantization of the gravitational field, which appears to be necessary for physical reasons, should be also possible using a formalism entirely equivalent to the one used here without new difficulties. (Heisenberg and Pauli 1929a, 3)
Now this quote doesn’t sound half as optimistic if the emphasis is put on new. For the theory of quantum electrodynamics which Heisenberg and Pauli had just constructed was replete with difficulties. Three of these difficulties will play an essential role in our story:
1The theory led to divergent expressions for the energies of stationary states. Even worse, J. Robert Oppenheimer, who was working with Pauli in Zurich at the time, could also show that the differences between these energies (i.e., the actually observed frequencies of spectral lines) came out infinite (Oppenheimer 1930).
2In order to write down a Lorentz-invariant Lagrangian for the interacting electromagnetic and matter-wave fields, it was necessary to work with the electromagnetic potentials
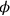 and not just with the fields. But the Lagrangian does not contain then a time derivative of the electric potential
and not just with the fields. But the Lagrangian does not contain then a time derivative of the electric potential
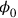 , so that there is no corresponding canonical momentum variable, preventing the straightforward implementation of canonical commutation relations.
, so that there is no corresponding canonical momentum variable, preventing the straightforward implementation of canonical commutation relations.
3The theory was not manifestly covariant due to the use of equal-time commutation relations. These allowed for a close analogy with the canonical commutation relations of non-relativistic quantum mechanics, but, by singling out time, destroyed manifest covariance. The Lorentz invariance of the theory thus had to be (and was) proven in a rather roundabout manner.
All three difficulties also played an important role in early work on the quantization of the gravitational field. I will be referring to these three difficulties as the divergence, the momentum, and the quantization difficulty, respectively. I will begin by discussing the momentum difficulty.
This difficulty was initially solved by Heisenberg and Pauli by adding to the Lagrangian additional terms, which contained a time derivative of
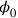 and were proportional to a parameter
and were proportional to a parameter
 , which was supposed to be set to zero in the final expressions for physical quantities. This procedure was viewed as rather artificial from the start. Heisenberg, who had cooked up the method,3 described it as a “very crude trick.”4 Heisenberg consequently devised a new method for Heisenberg and Pauli’s second paper on QED (Heisenberg and Pauli 1929b).5 This method relied on the notion of the gauge invariance of the theory of coupled electromagnetic potentials and Dirac matter waves
, which was supposed to be set to zero in the final expressions for physical quantities. This procedure was viewed as rather artificial from the start. Heisenberg, who had cooked up the method,3 described it as a “very crude trick.”4 Heisenberg consequently devised a new method for Heisenberg and Pauli’s second paper on QED (Heisenberg and Pauli 1929b).5 This method relied on the notion of the gauge invariance of the theory of coupled electromagnetic potentials and Dirac matter waves
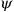 , which Weyl had only recently introduced (see the preceding part), that is, the invariance under a substitution
, which Weyl had only recently introduced (see the preceding part), that is, the invariance under a substitution

|
17.1 |

|
17.2 |
where
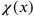 is an arbitrary space-time function. Heisenberg’s idea was the following: The field
is an arbitrary space-time function. Heisenberg’s idea was the following: The field
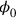 was simply not quantized, thereby eliminating the need for a canonically conjugate momentum variable in order to construct the canonical commutation relation.
was simply not quantized, thereby eliminating the need for a canonically conjugate momentum variable in order to construct the canonical commutation relation.
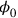 was then simply a (c-number) function of space-time and could be set to zero, due to the well-known underdetermination of the electromagnetic potential. This brought with it a new difficulty, however: With
was then simply a (c-number) function of space-time and could be set to zero, due to the well-known underdetermination of the electromagnetic potential. This brought with it a new difficulty, however: With
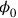 set to zero, the equation of motion for
set to zero, the equation of motion for
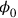 (which is simply the first Maxwell equation, or Coulomb’s law,
(which is simply the first Maxwell equation, or Coulomb’s law,
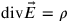 ) no longer resulted from the variation of the Lagrangian and the dynamical problem was underdetermined. The equation of motion could also not simply be added as an operator identity, because it would imply non-vanishing commutation relations between matter and electromagnetic field operators, in contradiction with the canonical commutation relations.
) no longer resulted from the variation of the Lagrangian and the dynamical problem was underdetermined. The equation of motion could also not simply be added as an operator identity, because it would imply non-vanishing commutation relations between matter and electromagnetic field operators, in contradiction with the canonical commutation relations.
Heisenberg now realized that one had not exploited the full gauge invariance by setting
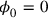 . There was still a residual gauge symmetry, since if the function
. There was still a residual gauge symmetry, since if the function
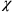 doesn’t depend on time
doesn’t depend on time
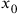 , the transformation 17.2 leaves
, the transformation 17.2 leaves
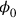 unaltered. To this residual symmetry now corresponded an operator that commutes with the Hamiltonian, that is, a conserved physical quantity. The conserved quantity corresponding to the residual gauge symmetry turned out to be
unaltered. To this residual symmetry now corresponded an operator that commutes with the Hamiltonian, that is, a conserved physical quantity. The conserved quantity corresponding to the residual gauge symmetry turned out to be
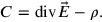
|
17.3 |
One could thus first solve the dynamical problem without the first Maxwell equation and then pick those solutions for which
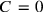 , that is, for which the first Maxwell equation was fulfilled at some initial time. There was thus a Nebenbedingung (subsidiary condition) on the initial quantum state
, that is, for which the first Maxwell equation was fulfilled at some initial time. There was thus a Nebenbedingung (subsidiary condition) on the initial quantum state
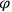 , which had to fulfill the equation
, which had to fulfill the equation
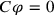 . Since
. Since
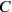 commutes with the Hamiltonian, this condition on the initial state would propagate, and the first Maxwell equation would always be fulfilled, without actually being an operator identity.
commutes with the Hamiltonian, this condition on the initial state would propagate, and the first Maxwell equation would always be fulfilled, without actually being an operator identity.
The central difficulty with this new method was the apparent lack of Lorentz invariance: There was now no commutation relation for the zero component of the electromagnetic potential four-vector, and hence the commutation relations were no longer covariant — this was in addition to the difficulty of the equal-time commutators, that is, the quantization difficulty. Heisenberg and Pauli convinced themselves that “all statements about gauge invariant quantities [...] fulfill the demand of relativistic invariance,” but the proof they presented was highly problematic.6
This was the state of affairs for the momentum difficulty, when Pauli finally turned to the quantization of gravity. The immediate stimulus appears to have been the reading of Weyl’s paper on the interacting theory of Dirac matter waves, electromagnetic potentials and the gravitational field (Chapter 12).7 He dismissed Weyl’s attempt to solve the problem of the negative energy states by using massless Weyl two-spinors instead of Dirac spinors, especially because he did not share Weyl’s hope that gravitational effects might be able to generate the mass term:
The hope of finding a replacement for the mass term in gravitational theory appears illusory to me; the gravitational effects will always be much too small numerically. (Hermann, Meyenn, and Weisskopf 1979, 519)
But Pauli realized that Weyl’s general scheme of coupling spinors to a curved space-time metric, by expressing the latter in terms of tetrads, would also work for regular, massive Dirac four-spinors.8 Reformulated in this manner, Weyl’s field theory provided a natural extension of the field theory of interacting matter and electromagnetic waves that Heisenberg and Pauli had quantized for their QED. It thereby provided the obvious starting point for extending and completing their work by also including the gravitational field. Pauli concluded his remarks on Weyl’s paper by stating:
What now interests me most, is the question of how to quantize the[the tetrads] themselves in your gravitational theory. (Hermann, Meyenn, and Weisskopf 1979, 520)
This was the question which he set his assistant Léon Rosenfeld. Rosenfeld soon discovered that one encountered problems akin to the momentum difficulty of QED.9 For example, the canonical momenta for the time-components of the four tetrad basis vectors identically vanished. In further pursuing this question, Rosenfeld obtained several interesting results, which he published in a lengthy paper in 1930 (Chapter 18).10 First of all, he was able to demonstrate in general that the momentum-type difficulties were the result of the invariance of the Lagrangian with regard to certain groups, the gauge group for the case of electrodynamics, the group of general coordinate transformations for general relativity, and the local Lorentz symmetry of the tetrad formulation. He then went on to devise a general method for dealing with such difficulties, a method which also managed to bypass the difficulties of Lorentz covariance encountered in the (second) Heisenberg-Pauli scheme.
In order to sketch Rosenfeld’s method, I will focus on the simple case of QED, which is the only example he really worked out to the end. The general idea was to also introduce canonical commutation relations for, and thereby to quantize, the electric potential
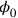 : Rosenfeld simply assumed that there existed a momentum operator
: Rosenfeld simply assumed that there existed a momentum operator
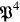 that did in fact obey the canonical commutation relation with the electric potential. In order to do this two points needed to be addressed.
that did in fact obey the canonical commutation relation with the electric potential. In order to do this two points needed to be addressed.
First, this meant that the Hamiltonian 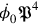 . In order to have the Hamiltonian expressed solely in terms of the canonical variables, one would have to express
. In order to have the Hamiltonian expressed solely in terms of the canonical variables, one would have to express
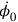 in terms of the canonical momenta (and the canonical coordinates, that is, the components of the potential). But the original Lagrangian did not depend on
in terms of the canonical momenta (and the canonical coordinates, that is, the components of the potential). But the original Lagrangian did not depend on
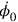 , and consequently
, and consequently
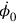 did not show up in the expressions relating the time derivatives of the field and the canonical momenta. This implied that
did not show up in the expressions relating the time derivatives of the field and the canonical momenta. This implied that
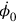 could be an arbitrary function of space and time without contradicting the defining equations for the canonical momenta. Rosenfeld thus set
could be an arbitrary function of space and time without contradicting the defining equations for the canonical momenta. Rosenfeld thus set
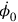 in the Hamiltonian equal to an arbitrary function
in the Hamiltonian equal to an arbitrary function
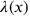 , which then consequently showed up in the equations of motion for the four-potential. In particular the equation of motion for the electric potential was simply of the form
, which then consequently showed up in the equations of motion for the four-potential. In particular the equation of motion for the electric potential was simply of the form
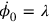 , ensuring the self-consistency of the approach. A specification of
, ensuring the self-consistency of the approach. A specification of
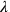 then corresponded to choosing a gauge.
then corresponded to choosing a gauge.
The second point was that one still needed to take account of the fact that the momentum conjugate to the electric potential was actually zero. Rosenfeld introduced a Heisenberg-Pauli type Nebenbedingung on the state, demanding that
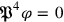 . And in order to have this condition propagate in time, an additional condition needed to be imposed
. And in order to have this condition propagate in time, an additional condition needed to be imposed
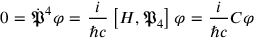
|
17.4 |
One thus obtained the same Nebenbedingung that Heisenberg and Pauli had imposed, ensuring the validity of Coulomb’s law. No further conditions were necessary, since
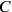 was a constant, as Heisenberg and Pauli had already shown.
was a constant, as Heisenberg and Pauli had already shown.
Since Rosenfeld’s scheme was essentially equivalent to the Heisenberg-Pauli method for the specific choice
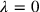 (although it should be noted that it was not actually necessary to specify
(although it should be noted that it was not actually necessary to specify
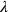 at all), Rosenfeld’s work in the context of QED could simply be viewed as a proof of the covariance of that method, and this is how he later presented it,11 resorting to the simpler Heisenberg-Pauli method for actual calculations (Rosenfeld 1932).
at all), Rosenfeld’s work in the context of QED could simply be viewed as a proof of the covariance of that method, and this is how he later presented it,11 resorting to the simpler Heisenberg-Pauli method for actual calculations (Rosenfeld 1932).
In any case, it was a whole different approach that came to be the standard method in the QED of the 1930s and 1940s, due to Enrico Fermi, which was based on taking the (Lorenz) gauge condition (as opposed to Coulomb’s law) and its time derivative as conditions on the wave function (Fermi 1932).12 It involved the use of a modified Lagrangian that was not gauge invariant and only returned the Maxwell equations if the Lorenz gauge was imposed. Rosenfeld argued against the Fermi approach in his paper, on account of its lacking gauge covariance, demonstrating that his own method was in fact gauge covariant. But this was not a very strong argument at the time, and also Rosenfeld could field no arguments as to why one should attach much weight to gauge covariance in the first place.
How then did Rosenfeld’s method fare in the context of gravitation? It did indeed prove applicable, in particular because it was generalizable to the case where the constraints on the canonical momenta were more complicated than the mere vanishing of some of the components, as was the case for the constraints arising from the local Lorentz covariance of the tetrad formalism. But he stopped short of actually constructing a canonical Hamiltonian for the Weyl-Fock field theory. For this, he would have had to solve the equations defining the canonical momenta for the time derivatives of the fields (i.e., of the tetrads), in order to end up with a Hamiltonian that only contained canonical coordinates and momenta, as well as the arbitrary functions of the type
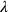 .
.
Why did Rosenfeld not do this? This question remains unanswered. Years later, Pauli remarked that Rosenfeld’s work was “not satisfactory in all aspects, because he had to introduce certain additional conditions, which no one could really understand.”13 It is entirely unclear, however, what Pauli was referring to. Rosenfeld’s work remained for the next two decades an anomaly, until the late 1940s, when the systematic study of constrained Hamiltonian dynamics picked up steam, and several of Rosenfeld’s results were re-discovered, as will be discussed in the final part of this book. One additional, simple result of Rosenfeld’s, unrelated to the momentum difficulty, has stood the test of time: The necessity of quantizing the gravitational field with commutators, that is, the realization that gravitons must be bosons. Ten years before Pauli’s formulation of the spin-statistics theorem, this was a non-trivial result.
One thing is certain: Solving the momentum relations for the time derivatives of the fields is a complicated business. This would not be the last instance of physicists convincing themselves that methods from QED also worked for gravity in principle, without filling in the details. In any case, it turned out to be unnecessary for Rosenfeld’s second work on the quantum theory of gravity, which he completed in the same year (Chapter 19). This second paper, much more than the first, which certainly started out as an attempt to quantize gravity, is an attempt to better understand the difficulties of QED by studying whether similar difficulties appeared in other quantum field theories. The difficulty in question here was the first difficulty mentioned above, the divergence difficulty, to which we will now turn.
It was initially unclear whether the divergence of the self-energy of the electron in QED was simply an inheritance from the classical theory, where it was well-known that the notion of a point electron was highly problematic, due to the infinite electromagnetic mass associated with such an object. Supposedly Heisenberg had suggested14 that one should study the case of the gravitational self-energy of the photon, since there were no singularities in the corresponding classical theory of an electromagnetic wave interacting with the gravitational field. In any case, Pauli egged Rosenfeld on to pursue this problem.15
The electromagnetic self-energy of the electron had been calculated perturbatively, expanding in terms of the coupling constant, the electron charge
 . The divergent expression then arose at second order in perturbation theory. Consequently, Rosenfeld performed his calculation of the gravitational self-energy of the photon in the approximation of a weak gravitational field. Such an approximation had, of course, been worked out by Einstein immediately after the formulation of general relativity (see the first part of this book). Einstein had started from the assumptions that the deviations
. The divergent expression then arose at second order in perturbation theory. Consequently, Rosenfeld performed his calculation of the gravitational self-energy of the photon in the approximation of a weak gravitational field. Such an approximation had, of course, been worked out by Einstein immediately after the formulation of general relativity (see the first part of this book). Einstein had started from the assumptions that the deviations
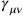 from the flat space-time metric were numerically small (compared to the elements of the flat space-time metric itself, which are of order 1). Rosenfeld now factored out a co-efficient
from the flat space-time metric were numerically small (compared to the elements of the flat space-time metric itself, which are of order 1). Rosenfeld now factored out a co-efficient
 , the square root of Einstein’s gravitational constant, the deviations from the flat space-time metric thus now being of the form
, the square root of Einstein’s gravitational constant, the deviations from the flat space-time metric thus now being of the form
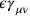 , Rosenfeld’s
, Rosenfeld’s
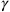 now being a dimensionful quantity. This explicitly made Einstein’s approximation equivalent to an expansion in terms of the gravitational coupling constant.
now being a dimensionful quantity. This explicitly made Einstein’s approximation equivalent to an expansion in terms of the gravitational coupling constant.
As Einstein had further remarked, solving the field equations of general relativity in this approximation was basically equivalent to calculating retarded potentials in electrodynamics. This also meant that all the techniques developed for QED could be taken over to the quantization of (linearized) gravity in a very straightforward manner. In particular, there was no need for Rosenfeld’s new method of dealing with the momentum difficulty.16 The Fermi method could be taken over from QED and applied directly to gravity, the Lorenz gauge condition being replaced by the analogous coordinate condition imposed by Einstein
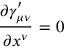
|
17.5 |
where
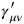 is the trace-reverse of
is the trace-reverse of
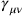 . Following Fermi, Rosenfeld constructed a Lagrangian which was not simply the linearized Einstein-Hilbert Lagrangian, and hence not even approximately invariant under general coordinate transformations. The most straightforward way to arrive at the Rosenfeld Lagrangian is to linearize the first-order Einstein-Hilbert Lagrangian, impose the above coordinate condition and then drop a total divergence. Rosenfeld presented no derivation of his Lagrangian, the only important point being that it returned the correct linearized field equations.
. Following Fermi, Rosenfeld constructed a Lagrangian which was not simply the linearized Einstein-Hilbert Lagrangian, and hence not even approximately invariant under general coordinate transformations. The most straightforward way to arrive at the Rosenfeld Lagrangian is to linearize the first-order Einstein-Hilbert Lagrangian, impose the above coordinate condition and then drop a total divergence. Rosenfeld presented no derivation of his Lagrangian, the only important point being that it returned the correct linearized field equations.
In this framework, Rosenfeld then calculated (to second order in
 ) the gravitational field energy in the absence of free gravitons, where the operator
) the gravitational field energy in the absence of free gravitons, where the operator
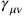 can be expressed solely in terms of the electromagnetic field operators. He obtained two divergent terms, one constant and one proportional to the number of photons. The second term was interpreted as the gravitational field energy of a photon, and its divergent nature was subsequently cited as proof for the quantum nature of the self-energy divergence, independent of the presence of singularities in the corresponding classical theory.
can be expressed solely in terms of the electromagnetic field operators. He obtained two divergent terms, one constant and one proportional to the number of photons. The second term was interpreted as the gravitational field energy of a photon, and its divergent nature was subsequently cited as proof for the quantum nature of the self-energy divergence, independent of the presence of singularities in the corresponding classical theory.
There remained the suspicion that this divergent energy was merely the coupling of the gravitational field to the infinite zero-point energy of the electromagnetic field. This question was investigated soon after by Jacques Solomon, who redid Rosenfeld’s calculation after first eliminating the zero-point energy in the Hamiltonian of the electromagnetic field by imposing normal ordering on the annihilation and creation operators (Solomon 1931). Solomon showed that while the constant divergent term was eliminated in this manner, the photon self-energy remained divergent. But he had only imposed normal ordering on the level of the electromagnetic Hamiltonian and this normal ordering did not survive when calculating the energy of the gravitational field. I therefore think that it can still be argued that Rosenfeld’s divergence was merely the result of the coupling to the zero-point energy.
In any case, when Rosenfeld’s calculation was redone again by Bryce deWitt (né Seligman) in his unpublished PhD thesis (DeWitt 1949), now using modern covariant techniques, he obtained a vanishing photon self-energy, as should be expected from considerations of gauge invariance alone. DeWitt gave no real argument as to where Rosenfeld had gone wrong, which is quite understandable considering that almost all the calculations from the 1930s were considered obsolete when renormalized quantum field theory was developed in the late 1940s.
The question of the photon self-energy aside, Rosenfeld was still interested in the general question of the quantization of gravity and supplemented his paper with a section on the quantization of the linearized gravitational field also for the case of free gravitons. His treatment was, however, quite sketchy. Bypassing the canonical commutation relations, Rosenfeld went straight to an explicit expression for the operator
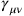 in terms of graviton annihilation and creation operators, by expanding in terms of transverse gravitational wave solutions of the free field equation. These transverse waves had been identified by Einstein as the only physical gravitational waves, carrying energy and propagating with the speed of light. Rosenfeld concluded with a brief look at graviton-photon scattering in this linear quantum theory of gravity.
in terms of graviton annihilation and creation operators, by expanding in terms of transverse gravitational wave solutions of the free field equation. These transverse waves had been identified by Einstein as the only physical gravitational waves, carrying energy and propagating with the speed of light. Rosenfeld concluded with a brief look at graviton-photon scattering in this linear quantum theory of gravity.
The quantization of linearized GR wasn’t worked out in detail until 6 years later, in the PhD work of Soviet physicist Matvei Bronstein (Chapter 20).17 It is unclear whether he was aware of Rosenfeld’s work,18 but he did not really need to build on it. Bronstein had an independent program of formulating linearized GR as close to electrodynamics as possible, with
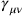 treated as a regular field in flat Minkowski space-time (as opposed to as a deviation from the flat space-time metric). He could then straightforwardly apply the canonical, equal-time field quantization procedure developed by Heisenberg and Pauli for QED (along with the Fermi method for dealing with the coordinate condition, which Bronstein now explicitly identified as a gauge condition) to all components of the linearized gravitational field, not only to those that corresponded to freely propagating waves.
treated as a regular field in flat Minkowski space-time (as opposed to as a deviation from the flat space-time metric). He could then straightforwardly apply the canonical, equal-time field quantization procedure developed by Heisenberg and Pauli for QED (along with the Fermi method for dealing with the coordinate condition, which Bronstein now explicitly identified as a gauge condition) to all components of the linearized gravitational field, not only to those that corresponded to freely propagating waves.
These additional components became important when treating the interaction with matter. Here, Bronstein built on Fock’s work, expressing Fock’s generally relativistic Dirac equation, and in particular the tetrads, in terms of the
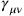 . Bronstein could thereby not only calculate the emission and absorption coefficients for transverse gravitons, but also show how the non-transverse gravitons led to a Newtonian gravitational interaction between electrons, in the same way that the longitudinal (and time-like) photons of QED led to the Coulomb interaction.
. Bronstein could thereby not only calculate the emission and absorption coefficients for transverse gravitons, but also show how the non-transverse gravitons led to a Newtonian gravitational interaction between electrons, in the same way that the longitudinal (and time-like) photons of QED led to the Coulomb interaction.
But Bronstein’s work is less known for his detailed treatment of the quantum theory of linearized gravity, and more for his musings on the full quantum theory of gravity. Bronstein transferred Bohr and Rosenfeld’s analysis of the measurability of field quantities in QED (Bohr and Rosenfeld 1933) to quantum gravity. Bohr and Rosenfeld had concluded that there were no further restrictions on the measurability of the electromagnetic field beside those arising from the canonical uncertainty relations, just as in quantum mechanics. This conclusion had centrally rested on the assumption that the test body used to measure the field was macroscopic (i.e., its atomistic nature could be disregarded) and could be given an arbitrarily high charge density. Bronstein argued that, although the close relation between QED and the quantum theory of gravity allowed adapting almost the entire Bohr-Rosenfeld analysis, the final conclusion would be different, because general relativity did not allow for arbitrarily dense bodies. Rather, there was a fundamental limit from the fact that a body could not become smaller than its gravitational (Schwarzschild) radius. There were thus absolute limits on the measurability of the gravitational field and a quantum theory of gravity would require major conceptual changes.
Now Bronstein’s reasoning clearly shows great physical intuition. He was the first to realize the essential difficulties inherent in constructing a quantum theory of gravity and that such a theory was not to be had without fundamental conceptual innovations. His argument is fielded to this day as an elementary demonstration of the problem that is quantum gravity. Why then was Bronstein’s argument hardly received by his contemporaries? To understand why it didn’t make much of a splash at the time, one needs to look at its weaknesses in somewhat more detail.
One objection was already raised at Bronstein’s thesis defense by Wladimir Fock:19 The absence of a fundamental restriction on the charge density was hardly a desirable feature of quantum electrodynamics. Rather, it allowed for a theory such as QED with point charges that had an apparently infinite charge density, resulting in the divergence difficulties discussed above. Physicists at the time were thus much more inclined to believe that revisions in the concepts of space and time would come from a reformed (quantum) electrodynamics, where a quantity of the order of the classical electron radius would play an essential role. The radical changes that Bronstein was envisioning were thus expected to come in at much larger length scales. It was only when the difficulties of QED (and then also of nuclear physics) had been solved — without radical changes in the underlying space-time theory—that Bronstein’s arguments could be viewed as convincing.20
But there is a more intrinsic difficulty in Bronstein’s argument as well. The aim of the Bohr-Rosenfeld analysis had been to take the established mathematical framework of QED and prove that it was internally consistent, that is, that there were no fundamental limitations on the observability of the electromagnetic field components, which would have been in contradiction with the initial choice of these components as the dynamical (quantum) variables. The Bohr-Rosenfeld analysis was thus a procedure to be applied to an already formulated quantum theory, in order to see whether it contained inherent contradictions. Consequently, in the original Russian article based on his thesis (Bronstein 1936), Bronstein applied this analysis to his linearized quantum gravity (which was a fully formulated quantum field theory), and not to an as yet hypothetical full quantum theory of gravity. He then voiced the hope that his argument would also carry over to the full theory, even though his analysis could not be applied to it, since it had not yet been formulated.
Somewhere between writing up his thesis and publishing the German-language article reprinted here, Bronstein must have realized that this argument was fundamentally flawed. There was nothing in the classical, linearized theory that prevented a body from being smaller than its gravitational radius. And so the linearized quantum theory was just as consistent as QED. In the German article, he thus presented the Bohr-Rosenfeld argument as an argument against the coherence of a quantum field theory based on the full non-linear theory of gravity, disregarding the obvious logical difficulty of showing the inconsistency of a theory that didn’t even exist yet.
This criticism of Bronstein’s argument was raised by Jacques Solomon (Chapter 21), but not without bringing forth a further argument against the possibility of constructing a quantum field theory based on the full non-linear theory.21 Solomon’s argument was based on a recent proof by Nathan Rosen on the non-existence of non-singular plane wave solutions in full GR (Rosen 1937).22 Now, all quantum field theories of the time were based on an expansion of the field quantities in plane waves. Even if Heisenberg and Pauli’s starting point had been commutation relations for the field quantities themselves, as soon as they went to the level of representing these field quantities as operators on a Hilbert space, they had, as they grudgingly admitted, no choice but to expand them in plane wave solutions of the free field equations and treat the expansion coefficients as annihilation and creation operators on occupation number space. From the absence of plane wave solutions, Solomon concluded that the present formalism of field quantization was not compatible with the non-linear theory of gravitation, a weaker claim than Bronstein’s, but one that found at least one interested listener in Pauli, as we shall see later.
But of course both Bronstein’s and Solomon’s thoughts on the difficulties of the non-linear quantum theory of gravity could be regarded as nitpicking, as long as the difficulties of QED (and thereby also of the quantum theory of linearized gravity) remained unsolved. The attempts to solve these difficulties, in as far as they were difficulties of quantum field theory in general, of course also impacted the pursuit of quantum gravity. It is well-known that the most fundamental difficulty of QED, the divergence difficulty, was not solved until the late 1940s. But progress was being made already in the 1930s on lesser difficulties, in particular on the lack of manifest covariance due to the use of equal time commutators, what I have called the quantization difficulty. In the last part of this essay, I will focus on this third and final difficulty.
While certainly not the most pressing difficulty at the time, there were enough physicists who believed that formulating quantum theory in a more overtly relativistic manner was a worthwhile endeavor. Two important relativistic quantization procedures were devised in order to replace equal-time commutators in the first half of the twentieth century.23 In both cases, Paul Dirac played an essential role. The union of relativity and quantum theory was a leitmotif in his work from the very start, when he attempted to make Heisenberg’s matrix mechanics relativistic by turning time into a non-commuting matrix (Dirac 1926). This was followed by the Dirac equation in 1928 (Dirac 1928) and then by several hugely influential papers in 1932/33, in which he laid the foundations for several new, relativistically invariant quantization techniques. We begin by discussing his 1933 paper on “The Lagrangian in Quantum Mechanics” (Dirac 1933).
Dirac’s general idea was to formulate quantum mechanics not in terms of states (wave functions) propagating in time, but in terms of transition amplitudes from the state at one time to the state at a later time. Dirac called these transition amplitudes “transformation functions,” since he conceptualized them as generating canonical transformations from the canonical coordinates at one time to those at a later time. In the final section, he also hinted at how to generalize this idea to quantum field theory, where the initial and final times would be replaced by an arbitrary (not necessarily space-like) three-dimensional hypersurface of space-time, which formed the integration boundary of the classical action. He dubbed the field theoretic amplitudes relating the canonical (field) coordinate values on different points on this hypersurface24“generalized transformation functions.” Dirac’s ideas, however, remained very vague and were not worked out in any detail by him.
Dirac’s idea was taken up by Paul Weiss,25 who realized that the procedure of replacing initial and final times by general three-dimensional boundary hypersurfaces might also be applicable to the canonical quantization procedure (Weiss 1936). At first sight, the canonical quantization procedure seemed to rest essentially on the singling out of time, since the momentum canonically conjugate to a field variable
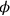 appearing in the Lagrangian
appearing in the Lagrangian
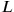 was defined as
was defined as
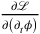 . This was one of the reasons why Dirac had based his sketch on the Lagrangian formalism, where the canonical momenta do not enter. Weiss now noted that the canonical momentum could also be defined in another way. If one reads the definition of the canonical momentum as the time component of the four-vector
. This was one of the reasons why Dirac had based his sketch on the Lagrangian formalism, where the canonical momenta do not enter. Weiss now noted that the canonical momentum could also be defined in another way. If one reads the definition of the canonical momentum as the time component of the four-vector
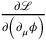 , then this can be generalized by taking the canonical momentum as the component of the four-vector orthogonal to the hypersurface forming the integration boundary of the action, on which the values of the field variables are fixed.
, then this can be generalized by taking the canonical momentum as the component of the four-vector orthogonal to the hypersurface forming the integration boundary of the action, on which the values of the field variables are fixed.
Weiss initially, like Dirac, took the boundary hypersurface to be closed. So, while one could locally determine the direction
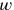 perpendicular to the surface and describe points on the surface by three parameters
perpendicular to the surface and describe points on the surface by three parameters
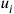 , this coordinate system (dubbed “natural” by Weiss) could not be regular throughout space-time. Still, one could write down commutators for the field operators, which were exactly of the form of the Heisenberg-Pauli equal-time commutators, except that the arguments of the field operators were now not the three spatial coordinates, but rather the three surface parameters
, this coordinate system (dubbed “natural” by Weiss) could not be regular throughout space-time. Still, one could write down commutators for the field operators, which were exactly of the form of the Heisenberg-Pauli equal-time commutators, except that the arguments of the field operators were now not the three spatial coordinates, but rather the three surface parameters
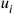 . Further, a Hamiltonian could be constructed in the usual fashion, using the generalized canonical momenta, and be shown to generate the “time evolution” (i.e., the evolution for increasing
. Further, a Hamiltonian could be constructed in the usual fashion, using the generalized canonical momenta, and be shown to generate the “time evolution” (i.e., the evolution for increasing
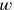 ) of the field operators.
) of the field operators.
In his second, and most influential paper (Chapter 22) , Weiss could show that the generalization of the commutation relations need not necessarily occur only at the quantum level, where it smacked of an ad-hoc modification of the well-established canonical quantization procedure. Instead, he could demonstrate that his generalized commutation relations corresponded already at the classical level to generalized Poisson brackets, and that his method was thus a straightforward generalization of the usual canonical quantization method.
This reconceptualization brought with it a slight modification of the original method. If the generalized Poisson brackets are supposed to be invariant under canonical transformations, in particular under time evolution, as are their point-mechanical counterparts, they can only sensibly be defined on some initial space-like hypersurface (on which then the values of both the field variables and the canonical momenta are given). Weiss thus dropped his original approach of having the commutation relations defined on an entire closed hypersurface, and replaced it with commutation relations on some (initial) space-like hypersurface, which corresponded to the classical, generalized Poisson bracket. This quantization procedure provided a covariant generalization of the equal-time commutators that, however, still stuck closely to the canonical scheme. We will discuss its further use in the last part of this book, which discusses the beginnings of what would come to be known as the canonical quantization approach to quantum gravity.
The other quantization procedure that went beyond the Heisenberg-Pauli equal-time commutators was not a direct generalization of the canonical quantization procedure, as Weiss’s method was. At its core were not the commutation relations between canonically conjugate field variables, but rather the commutation relations between two field variables at arbitrary different points in space-time. Such covariant commutators had first been used in 1928 by Jordan and Pauli for their quantization of the free electromagnetic field (Jordan and Pauli 1928). They were constructed by expanding the electromagnetic field variables in terms not of time-independent spatial modes, but in terms of time-dependent, propagating plane waves, which were solutions of the (free) equations of motion. Imposing the usual annihilation-creation operator commutation relations on the expansion coefficients, and then re-summing, the covariant commutation relations were obtained.
Since the construction was based on an expansion in terms of solutions of the wave equation, the commutation relations were automatically compatible with the equations of motion, a necessary requirement for any equation relating the field at two time-like (or, for the case of electrodynamics more importantly, light-like) separated points. Indeed, the commutators themselves actually had to be (singular) solutions of the equations of motion. This immediately became intractable once one was dealing with interacting fields and non-linear equations of motion, which is why one year later, Pauli reverted to the use of equal-time commutators.
Covariant commutation relations were brought back into the game by Dirac in 1932. In an attempt to relaunch QED, he had effectively reconstructed Heisenberg-Pauli quantum field theory, only now in the interaction representation (Dirac 1932). Dirac was much ridiculed by Pauli for having merely produced an equivalent theory, despite his grandiloquent claims to the contrary. In a letter to Dirac of 11 September 1932,26 Pauli wrote:
Your remarks on quantum electrodynamics [...] were—to put it mildly—certainly no masterpiece. After a confused introduction, consisting of sentences that were only halfway understandable because they were only halfway understood, you finally arrive at results for a simplified, one-dimensional example that are identical with those obtained by applying the formalism of Heisenberg and myself to this example. (The identity is immediately recognizable and was then calculated in too complicated a manner by Rosenfeld.) This conclusion of your work stands in contradiction to the more or less clearly voiced claims in the introduction that you would somehow be able to make a better quantum electrodynamics than Heisenberg and myself. (Hermann, Meyenn, and Weisskopf 1985, 115)
But when Dirac, together with Vladimir Fock and Boris Podolsky, actually applied his interaction representation formulation of quantum field theory to the full electrodynamics (Dirac, Fock, and Podolsky 1932), and not just to the toy example of the first paper, Pauli realized that it had a huge advantage: All the non-trivial dynamics due to the interaction between charged matter and electromagnetic field were relegated to the time evolution of the state vector. In other words: Also the second inhomogeneous Maxwell equation, the Ampère-Maxwell law, was satisfied only through the action of the field operators on the wave function and not as an operator identity. This implied that the electromagnetic field operators still obeyed the free field equations and consequently the covariant commutation relations of Jordan and Pauli. On 2 June 1933, Pauli wrote to Heisenberg:
As time goes by, I find myself liking the work of Dirac, Fock and Podolsky more and more. It is funny that there the commutation relations of vacuum electrodynamics do not change when particles are present, even for. (Hermann, Meyenn, and Weisskopf 1985, 167)
But the method of quantizing by imposing covariant commutation relations was still an isolated technique, applied only to the Maxwell field, far-removed from the generality of the canonical quantization approach, which could be applied to any classical field theory given in Lagrangian or Hamiltonian form. It was extended in 1938 by Stueckelberg to encompass massive scalar fields, again by explicitly expanding the field operators in terms of solutions of the wave equation (in this case the Klein Gordon equation) (Stückelberg 1938a), and then also to massive vector (Proca) fields (Stückelberg 1938b). In 1939, finally, Markus Fierz gave a general expression for the covariant commutation relations for fields with arbitrary spin (Fierz 1939).27 The covariant quantization method thereby became a full-fledged quantization method in its own right, applicable to any Lorentz-covariant field theory.
What did this mean for the quantization of gravity? General Relativity was, of course, not a Lorentz-invariant field theory, but as we have seen, the linearized theory could be thought of in this manner. And indeed, Fierz together with Pauli could show that the linearized gravitational field fit into Fierz’s scheme, namely as a massless spin 2 field (Chapter 23).
This was a major conceptual change: Bronstein (and Rosenfeld) had started from the full theory of general relativity and obtained a Lorentz-covariant field theory as an approximation. Pauli and Fierz now showed that one could construct the field theory of linearized gravity equally well without any reference to general relativity: it was the unique Lorentz-covariant field theory of a massless spin 2 field. Also the transformation properties of the metric perturbations
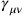 arose, without any reference to general coordinate transformations, as the gauge transformation properties of a massless field, a straightforward generalization of electrodynamics.
arose, without any reference to general coordinate transformations, as the gauge transformation properties of a massless field, a straightforward generalization of electrodynamics.
Initially, of course, this change was hardly consequential: The quantum field theory of linearized gravity had already been worked out, and neither the use of covariant quantization methods, nor the reconceptualization in terms of a spin 2 field made any difference to, say, Bronstein’s formulation. But it would eventually lead to a new way of thinking about the quantum theory of non-linear gravity. Pauli, when recapitulating his work with Fierz in his manuscript for the 1939 Solvay conference (which never took place due to the outbreak of World War II, but is reprinted in Meyenn (1993)), was still quite pessimistic concerning the prospects for the non-linear theory. In particular he cited Solomon’s argument, but with an interesting twist:
It is certainly a limitation of the quantum theoretical side of these considerations that one here contents oneself with the approximation in which the generally relativistic field equations are linear. This limitation is intimately connected with the well-known divergence difficulties of field theory. (Meyenn 1993, 901)
No further explanation of this connection is given, but I would suggest the following reading: In quantum electrodynamics it is the non-linear terms, that is, the terms coupling the electromagnetic field to the charged current of the electrons, that lead to the divergence difficulties. Pauli’s connection of the non-linearities of GR with the divergence difficulties of QED thus offered an entirely new way to look at these non-linearities: For Solomon, these were terms arising in a higher approximation to the full theory, spoiling the usual quantum field theoretical approach by eliminating the possibility of plane wave solutions. In contrast, the non-linear terms could now be considered as interaction terms, added on to the Lagrangian for the free spin 2 field, just like the interaction terms of QED were added on to the free field Lagrangians, with the sole difference that one was now talking about self-interactions of a single field.
As long as the divergence difficulties of QED remained unresolved, this hardly made a difference. But when covariant renormalization was developed in the late 1940s, it seemed plausible that the same techniques might also be used for the non-linear theory. By using the interaction representation, one could quantize the gravitational field in the same manner as the electromagnetic field, by separating the free spin 2 quantum (which had plane wave solutions, thereby circumventing Solomon’s objection) from its self-interaction. The self-interaction (as well as the interactions with the matter fields) could then be treated in the same manner as the interactions of QED, possible divergences being absorbed into the properties of the free field. Thus the program of covariant quantization was born, which, however, took off only somewhat after the period covered in this book. We thus see how the two major programs for the quantization of gravity, canonical and covariant quantization,28 had their origins in the 1930s, in two attempts to get over the quantization difficulty of QED with, at this early stage, only weak and incidental connections to the specific problem of quantum gravity.
References
Blum, Alexander (2014). “From the Necessary to the Possible: The Genesis of the Spin-Statistics Theorem.” European Physical Journal H 39 (5): 543–74.
Bohr, Niels, and Leon Rosenfeld (1933). “Zur Frage Der Messbarkeit Der Elektromagnetischen Feldgrößen.” Det Kgl. Danske Videnskabernes Selskab Mathematisk-Fysiske Meddelelser 12: 3–65.
Bondi, Hermann, Felix A. E. Pirani, and Ivor Robinson (1959). “Gravitational Waves in General Relativity. III. Exact Plane Waves.” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 251 (1267): 519–33.
Bronstein, Matwei Petrowitsch (1936). “Kvantovanie Gravitatsionn’ikh Woli.” Zhurnal Eksperimental’noj I Teoreticeskoj Fiziki 6 (3): 195–236.
Cassidy, David (1992). Uncertainty: The Life and Science of Werner Heisenberg. New York: W. H. Freeman.
Cini, Marcello (1982). “Cultural Traditions and Enviromental Factors in the Development of Quantum Electrodynamics (1925–1933).” Fundamenta Scientiae 3: 229–53.
Darrigol, Olivier (1982). “Les débuts de la théorie quantique des champs. 1925–1948.” PhD thesis, Université de Paris I.
——— (1986). “The Origin of Quantized Matter Waves.” Historical Studies in the Physical and Biological Sciences 16: 197–253.
DeWitt, Bryce (1949). “I: The Theory of Gravitational Interactions. II: The Interaction of Gravitation with Light.” PhD thesis, Harvard.
Dirac, Paul A. M. (1926). “Relativity Quantum Mechanics with an Application to Compton Scattering.” Proceedings of the Royal Society, Series A 111 (758): 405–23.
——— (1927). “The Quantum Theory of Emission and Absorption of Radiation.” Proceedings of the Royal Society of London A114: 243–65.
——— (1928). “The Quantum Theory of the Electron.” Proceedings of the Royal Society of London: Series A, Containing Papers of a Mathematical and Physical Character. JSTOR, 610–24.
——— (1932). “Relativistic Quantum Mechanics.” Proceedings of the Royal Society, Series A 136 (829): 453–64.
——— (1933). “The Lagrangian in Quantum Mechanics.” Physikalische Zeitschrift Der Sowjetunion 3 (1): 64–72.
Dirac, Paul A. M., Vladimir A. Fock, and Boris Podolsky (1932). “On Quantum Electrodynamics.” Physikalische Zeitschrift Der Sowjetunion 2 (6): 468–79.
Fermi, Enrico (1929). “Sopra L’elettrodinamica Quantistica.” Rendiconti Lincei 9: 881–87.
——— (1932). “Quantum Theory of Radiation.” Review of Modern Physics 4: 87–132.
Fierz, Markus (1939). “Über Die Relativistische Theorie Kräftefreier Teilchen Mit Beliebigem Spin.” Helvetica Physica Acta 12: 3–37.
Gorelik, Gennady E., and Victor Ya. Frenkel (1994). Matvei Petrovich Bronstein and Soviet Theoretical Physics in the Thirties. Basel: Birkhäuser.
Heisenberg, Werner, and Wolfgang Pauli (1929a). “Zur Quantendynamik Der Wellenfelder.” Zeitschrift Für Physik 56: 1–61.
——— (1929b). “Zur Quantentheorie Der Wellenfelder. Band Ii.” Zeitschrift Für Physik 59 (3–4): 168–90.
Hermann, Armin, Karl von Meyenn, and Victor F. Weisskopf, eds. (1979). Wolfgang Pauli: Wissenschaftlicher Briefwechsel Mit Bohr, Einstein, Heisenberg U.a. Vols. Vol. 1: 1919–1929. New York: Springer.
———, eds. (1985). Wolfgang Pauli: Wissenschaftlicher Briefwechsel Mit Bohr, Einstein, Heisenberg U.a. Vols. Vol. 2: 1930–1939. New York: Springer.
Jordan, Pascual, and Wolfgang Pauli (1928). “Zur Quantenelektrodynamik Ladungsfreier Felder.” Zeitschrift Für Physik 47: 151–73.
Kobzarev, Igorʹ Ju., ed. (1985). Einsteinovski Sbornik, 1980–1981. Moscow: Nauka.
Meyenn, Karl von, ed. (1993). Wolfgang Pauli: Wissenschaftlicher Briefwechsel Mit Bohr, Einstein, Heisenberg U.a. Vols. Vol. 3: 1940–1949. Berlin: Springer.
———, ed. (2001). Wolfgang Pauli: Wissenschaftlicher Briefwechsel Mit Bohr, Einstein, Heisenberg U.a. Vols. Vol. 4, Part 3: 1955–1956. Berlin: Springer.
Misner, Charles W. (1957). “Feynman Quantization of General Relativity.” Reviews of Modern Physics 29 (3): 497–509.
Oppenheimer, J. Robert (1930). “Note on the Theory of the Interaction of Field and Matter.” Physical Review 35 (5): 461–77.
Rickles, Dean, and Alexander Blum (2015). “Paul Weiss and the Genesis of Canonical Quantization.” European Physical Journal H 40 (4–5): 469–87.
Rosen, Nathan (1937). “Plane Polarised Waves in the General Theory of Relativity.” Physikalische Zeitschrift Der Sowjetunion 12: 366–72.
Rosenfeld, Leon (1932). “La Théorie Quantique Des Champs.” Annales de L’Institut Henri Poincaré 2 (1): 25–91.
Rovelli, Carlo (2004). Quantum Gravity. Cambridge: Cambridge University Press.
Rueger, Alexander (1992). “Attitudes Towards Infinities: Responses to Anomalies in Quantum Electrodynamics, 1927–1947.” Historical Studies in the Physical and Biological Sciences 22: 309–37.
Salisbury, Donald (2009). “Léon Rosenfeld and the Challenge of the Vanishing Momentum in Quantum Electrodynamics.” Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 40 (4): 363–73.
Schweber, Silvan S. (1994). QED and the Men Who Made It: Dyson, Feynman, Schwinger, and Tomonaga. Princeton: Princeton University Press.
Solomon, Jacques (1931). “Nullpunktsenergie Der Strahlung Und Quantentheorie Der Gravitation.” Zeitschrift Für Physik 71 (3–4): 162–70.
Stachel, John (1999). “The Early History of Quantum Gravity (1916–1940).” In Black Holes, Gravitational Radiation and the Universe, 525–34. Springer.
Stückelberg, Ernst C. G. (1938a). “Die Wechselwirkungskräfte in Der Elektrodynamik Und in Der Feldtheorie Der Kernkräfte: Teil 1.” Helvetica Physica Acta 11 (225–244).
——— (1938b). “Die Wechselwirkungskräfte in Der Elektrodynamik Und in Der Feldtheorie Der Kernkräfte: Teil 1fte in Der Elektrodynamik Und in Der Feldtheorie Der Kernkräfte: Teil 2 Und 3.” Helvetica Physica Acta 11: 299–328.
Weiss, Paul (1936). “On the Quantization of a Theory Arising from a Variational Principle for Multiple Integrals with Application to Born’s Electrodynamics.” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 156 (887): 192–220.
Footnotes
For the early history of quantum field theory, see, e.g., Cini (1982); Darrigol (1982; 1986) and the first two chapters of Schweber (1994). The difficulties of early quantum field theory are discussed in Rueger (1992). An overview that places the development of quantum field theory in the larger context of the development of quantum mechanics can be found in a chapter by Christoph Lehner and the author in a forthcoming volume on the genesis of quantum mechanics.
As opposed to free quantum electrodynamics on the one hand (Jordan and Pauli 1928), and quantum radiation theory, i.e., a theory of transverse photons, on the other (Dirac 1927).
See a letter from Pauli to Niels Bohr, 16 January 1929. All the Pauli letters from the 1920s are reprinted in Hermann, Meyenn, and Weisskopf (1979). All translations are by me.
Heisenberg to Jordan, 22 January 1929, Archive for the History of Quantum Physics, MF 18, Section 002–024.
See also a letter from Heisenberg to Pauli, 20 July 1929.
Dirac in a letter to Rosenfeld from 6 May 1932 (Niels Bohr Archive, Copenhagen) (under)stated that he found it “difficult to understand,” and Rosenfeld concurred on 10 May (Dirac Papers, Churchill College, Cambridge) that Dirac was “right in not understanding” the “highly doubtful sentence” with which Heisenberg and Pauli concluded their proof.
Letter from Pauli to Weyl, 26 August 1929.
This is of course what Fock had already done. But Pauli was not aware of Fock’s work until somewhat later. See a letter to Ehrenfest from 29 September 1929.
Letter from Pauli to Jordan, 30 November 1929.
For a detailed discussion of this work, in particular with regard to its relation with later work on constrained Hamiltonian dynamics, see Salisbury (2009).
Letter to Dirac, 21 May 1932, Dirac Papers, Churchill College, Cambridge.
It should be noted that Fermi himself actually gave no indications as to how exactly the gauge condition should be interpreted in his original work (Fermi 1929). It was only Heisenberg and Pauli who interpreted it as a condition on the state, akin to their own Nebenbedingung, an interpretation which Fermi then adopted.
... nicht in jeder Hinsicht befriedigend war, da er gewisse zusätzliche Bedingungen einführen musste, die niemand richtig verstehen konnte. Letter to Oskar Klein, 25 January 1955, reprinted in Meyenn (2001).
When and where is uncertain. Pauli in a letter to Rosenfeld (19 September 1930, but reprinted in Meyenn (1993)) speculates that it might have been during discussions in Copenhagen, but Heisenberg did not actually attend the 1929 spring conference in Copenhagen (8–15 April, see the timeline in Hermann, Meyenn, and Weisskopf (1979)), since he was on his world tour (from which he only returned in November, see the timeline in Cassidy (1992)).
Interview of Léon Rosenfeld by Thomas Kuhn and John Heilbron, Niels Bohr Library and Archives, American Institute of Physics, College Park, MD, USA, https://www.aip.org/history-programs/niels-bohr-library/oral-histories/4847-2 (accessed 21 July 2017).
It of course also needs to be noted that there was no need to introduce the tetrads in this case, since no spinorial matter was involved.
He was certainly aware of Rosenfeld’s first paper: During Bronstein’s thesis defense (the protocol is reprinted in Kobzarev (1985, 317–320)), Igor Tamm recommended that he make reference to it, which he did in the published Russian paper. Rosenfeld’s second paper on linearized gravity is, however, never mentioned.
Gorelik and Frenkel are somewhat dismissive of Fock’s objection, because they focus too narrowly on a specific attempt at introducing the electron radius into electrodynamics, the Born-Infeld theory, as did Bronstein in his reply to Fock. However, Fock explicitly stated that “the generalzation [of electrodynamics] to a non-linear theory is only beginning” (Kobzarev 1985, 318). He was thus referring to the general program and not merely to its specific, and problematic, implementation by Born and Infeld.
In the secondary literature, e.g. in Stachel (1999), Solomon’s and Bronstein’s arguments have in general been lumped together.
Rosen’s conditions were later seen as too strict, since he was also ruling out mere coordinate singularities (Bondi, Pirani, and Robinson 1959).
Not counting Feynman’s path integral, which was not applied to the case of gravitation until the mid-1950s, see in particular Misner (1957).
They should not be called transition amplitudes, since this would imply a notion of initial and final state. Maybe “correlation amplitudes” would be a good name.
The context of these works is the discovery of the putative Yukawa meson in 1937, see Blum (2014).
