Chapter structure
- 3.1 The General Principle: The Figure of the Circle
- 3.2 The Balance: Questions 1–2, 9–10 and 20
- 3.3 The Lever: Questions 3, 21–22, 28
- 3.4 Problems Concerning Sailing: Questions 4–7
- 3.5 The Easy Movement of Bodies with Round Shapes: Question 8
- 3.6 The Simple Machines. The Axle in the Wheel, the Pulley and the Wedge: Questions 11, 13, 17–18
- 3.7 The Sling: Question 12
- 3.8 The Breaking and Deformation of Materials. Pieces of Wood and Pebbles: Questions 14–16
- 3.9 The Force of Percussion: Question 19
- 3.10 The Composition of Motions: Questions 23–24
- 3.11 The Construction of Beds: Question 25
- 3.12 The Placement of Weights Carried on the Shoulders: Questions 26–27, 29
- 3.13 Rising from a Sitting Position: Question 30
- 3.14 Problems Concerning Motion: Questions 31–34
- 3.15 The Motion of Bodies in Eddying Water: Question 35
- 3.16 Appendix: The Problem of the Two Mean Proportionals
- Footnotes
Bernardino Baldi most probably began his study of ancient texts on mechanics when he was young. With Guidobaldo del Monte he continued the mathematical studies he had started under the guidance of Commandino and soon turned to study Archimedes' and Pappus' works. He produced a new Latin translation of Pappus' Book Eight of Mathematical Collections, and then moved on to work on the Mechanical Problems.1 Biographers of Baldi, such as Affò and Crescimbeni, mention the titles of at least three works on the Aristotelian text: Discorsi sopra le Meccaniche d'Aristotile, Dissertationes in mechanica problemata Aristotelis,2 and Exercitationes, but unfortunately none of the manuscripts containing these works have survived and the only available text is that of the 1621 edition of Exercitationes.3
It is likely that this work had already been written around 1582, but it was taken up again in 16144 and eventually entrusted in 1615 to Adriaan van Roomen so that he could have it printed in Germany.5 Van Roomen's death on May 4 of the same year delayed the publication of Baldi's work, which was published only in 1621, four years after the death of its author who had been unable to recover it. The text was full of misprints and incorrect figures, so as to require the addition of eight pages of errata corrige, which are extant in only a few of the surviving copies.6
To give a clear idea of the contents of this important work of Renaissance mechanics, the various questions contained in it have been arranged in groups according to similar topics. Some of these groupings appeared as such in the original text; others have been formed in order to give a clearer structure to the whole treatise. Since Baldi's work has the form of a commentary, it has been necessary to quote the questions as originally stated in the ancient text.
1The general principle: the figure of the circle.
2The balance (Questions 1–2, 9–10, 20).
3The lever (Questions 3, 21–22, 28).
4The problems concerning sailing (Questions 4–7).
5The easy movement of bodies with round shapes (Question 8).
6The simple machines: the axle in a wheel, the pulley and the wedge (Questions 11, 13, 17–18).
7The sling (Question 12).
8The breaking and deformation of materials: pieces of wood and pebbles (Questions 14–16).
9The force of percussion (Question 19).
10The composition of motions (Questions 23–24).
11The construction of beds (Question 25).
12The placement of weights carried on the shoulders (Questions 26–27, 29).
13The rising from a sitting position (Question 30).
14Problems concerning motion (Questions 31–34).
15The motion of bodies in eddying water (Question 35).
3.1 The General Principle: The Figure of the Circle
Baldi criticizes some of the main principles of Aristotelian mechanics, that is, those concerning the `marvellous' peculiarities of the circle, and shows that they are not based on the combination of opposites with each other. Following Archimedes he considers the entire mechanical science as based on the theory of the center of gravity, of which he gives a definition different from those given by Pappus and Commandino.7 In his definition he specifies that the center of gravity of a body “is a point placed inside or outside its magnitude.”8 He shows that in the case of arches, which are discussed in Question 16, the center of gravity is indeed placed in the outside space enclosed by the object and not inside the shape of the object. Within the discussion of the principles of the circle, Baldi was the first to determine the exact ratio in the composition of motions resulting in a circular motion. When Baldi discusses the reason why, according to Aristotle, the weight of the lever added to the weight to be moved makes the action of the moving power easier, he points out that this is true only in the case of the type of lever considered in the text, that is, a lever in which the fulcrum is placed between the weight and the moving power.
3.2 The Balance: Questions 1–2, 9–10 and 20
The first question, which asks why larger balances are more accurate than smaller ones, was presented by the author of Mechanical Problems in order to give an example of the fourth peculiarity of the circle, that is, that the points on the diameter describing the circle move more quickly the more distant they are from the center. This peculiarity of the circle is only stated, but not demonstrated in the Aristotelian text. Baldi gives a rigorous geometrical demonstration of this using the example of the astrolabe, which is more precise the greater its radius.9
In the second question it is asked why, if the support of a balance is fixed from above, does the balance revert back to its original position of equilibrium after the beam has inclined and the weight is removed; on the other hand, if the support is placed below the beam after it has been inclined, why does it not return to its original position. Baldi points out that the possible cases are not two, but three, according to the support being placed above the beam, below it or at its center of gravity.10 He then explains, on the basis of the theory of the center of gravity, the different ways in which the three types of balance behave and adds some interesting theorems concerning their different sensitivities. He discusses the situation of equilibrium of different bodies, such as the sarissa or long lance and the spinning top, as well as the wonderful case of the equilibrium of a little cardboard figure representing a tightrope-walker holding as a balancing pole a wire with two little lead spheres fixed at either end. Finally he gives an explanation for the great power of the battering ram.
The ninth question can be connected with a question discussed at the beginning of this work. It asks: “why can weights be raised more easily by means of larger pulleys than by smaller ones?” The explanation given is that pulleys with greater diameters work like balances with longer arms: in both cases things are moved and raised more easily and more quickly by means of greater diameters, which at the same time describe greater circles. Baldi agrees with the idea to relate the pulleys to the balance, but disagrees with the other aspects of the explanation. Referring to a proposition in Guidobaldo's Mechanicorum liber,11 he points out that ease of motion is contrary to the speed (with which it is done), that is, in modern terms, in machines the product of the force and the distance is constant. However, Baldi agrees with Aristotle that in practice pulleys with larger diameters work better. This is due to the ratio between the diameter of the pulley and the diameter of the axis: the greater this ratio, the easier the motion. The friction between the axis and the wheel of the pulley is also to be considered: such friction is more easily overcome by pulleys with larger wheels.
In the second part of his commentary to this question, Baldi discusses a topic so far ignored, that is, the case of wheels turned by a crank operated by hand or by foot. As with the lever, here as well the greater the ratio between the crank arm and the radius of the wheel axe, the easier the movement. There are two types of crank: those moved by hand with a straight arm, and those moved by foot with a bent arm. Referring to the example of the knife-grinder and his grindstone, Baldi asks why the grindstone moved by foot is fitted with a bent arm: he points out that, in modern terms, the bending of the arm helps to overcome the upper dead point. Finally, he examines two wheels of equal dimensions but of different weights turning on equal axes: he asks why the lighter wheel is moved more easily, but stops earlier. The reason given is that the heavier wheel at the beginning has greater resistance to the impressed force, but afterwards retains it for a longer time.
Question 10 asks: “why is a balance moved more easily when it is without a weight than when it has one?” Here the author of Mechanical Problems introduces an idea that later in the seventeenth century would be treated with the help of the concept of inertia. He asks why a balance with a lighter arm is more easily moved than one with a heavier arm. The reason given is that a heavier weight is more difficult to move, not only in the opposite direction, but also when it is at an angle. The Aristotelian explanation is considered insufficient by Baldi, who points out that the argument is in contrast to the experience of adding a given weight to two balances which are in equilibrium with different weights. In the Aristotelian work, the question was raised not only in connection with balances, but also in relation to wheels and other similar bodies. The Latin text presented by Baldi ought to be corrected by checking Tomeo's translation.12
Textual problems also occur in Question 20 concerning the steelyard, where a whole line of the original text is missing.13 The steelyard is a balance with unequal arms: the body to be weighed is suspended from the shorter arm and a counterpoise can be moved along the longer arm until equilibrium is reached. The author asks why a steelyard can weigh heavy pieces of meat with a small weight. The answer given by the author is that the steelyard can be considered as both balance and lever at the same time, and be reduced to the figure of the circle. Baldi has no objections to the reduction of the steelyard to the lever and simply points out that in theory this instrument can be used in two different ways: either by keeping the fulcrum fixed and making the counterpoise slide to a different position, or by keeping the counterpoise fixed and changing the position of the fulcrum. But he warns that in practice the steelyard is used in the first way.
3.3 The Lever: Questions 3, 21–22, 28
Recalling what has been said at the beginning of the work, Question 3 asks why small forces can move heavy weights by means of a lever. The Aristotelian solution consists in making the lever equivalent to the beam of a balance with its support placed below and stating that the greater the distance of the power from the fulcrum, the more easily the weight can be moved because, under the impulse of the same weight, the greater the radius is from the center, the more rapidly it moves. Baldi, however, rejects the idea that speed can be considered as the cause for the working of the lever because it was inconceivable for him to explain the equilibrium of the balance by referring to motion. The Aristotelian distinction between `actually' (actu) and `potentially' (potentie) did not allow something at rest to be considered as `potentially' in motion. The true explanation, according to Baldi, had been given by Archimedes in Proposition 6 of Book One of his work On the Equilibrium of Planes, though it would be necessary to indicate the cause of the inverse proportion stated in that proposition. For Baldi, the ultimate justification for the Archimedean law of the lever is the `equality of status' resulting from placing equal powers at the ends of a straight line in a given position.
As to the working of the dental forceps and nutcrackers analyzed in Questions 21 and 22, both instruments were regarded by the ancient author as formed by two levers working in opposite directions, having the point of junction as the fulcrum. Baldi follows here the explanation of Piccolomini.14
In Question 28 the author analyzes the working of the swing-beam (shaduf) used to draw water from a well, but without relating the structure of this machine to the lever.15 He points out that the operation normally occurs in two stages and that the empty bucket can easily be let down whereas it is difficult to draw it up when it is full. The disadvantage of letting it down more slowly with the help of this machine is balanced by the advantage of reducing its weight when drawing it up: this result is produced by a stone attached to the end of the swing-beam. Piccolomini and other authors after him felt the need to give a true mechanical explanation of the working of this machine, showing that it is based on the principle of the lever.16 To this explanation, Baldi added the remark that one also has to take into account the weight of the body of the man who lets down the empty bucket by lifting the loaded end of the beam.
3.4 Problems Concerning Sailing: Questions 4–7
In Question 4, the author asks why the rowers placed mid-ship are those who mostly move it. This is explained by considering the oar as acting like a lever where the thole pin is the fulcrum, because it is fixed, the sea is the weight, and the sailor is the force that moves the lever. The explanation is again based on the principle of the lever: in proportion to the increasing distance of the moving force from the fulcrum, the weight will move more. Baldi points out, however, that the fulcrum is not actually the thole pin, but the sea, whereas the ship is the weight placed at the thole pin, that is, between the power and the fulcrum. This is the kind of lever discussed by Guidobaldo in Proposition 2 of his treatise De vecte contained in Mechanicorum liber:17 here the weight is placed between the fulcrum and the power, and the ratio of the power to the weight is the same as that of the distance of the weight from the fulcrum to the distance of the power from the fulcrum. However, Baldi points out that Aristotle's argument would be conclusive if the ship were kept still by some hindrance: in this case the oar would move in the way described in the text, that is, the fulcrum would be placed at the thole pin and the weight would be the sea. Baldi argues moreover that it would be more correct to say that the rowers move the ship `more easily' rather than `mostly.'18
The following Question 5 asks why the rudder, which is small and at the end of the vessel, has such great power that the large mass of the ship can be moved by a small tiller and by the strength of one single man exerting just a small effort. The answer given is that the rudder is a lever, the sea the weight and the helmsman the moving power. The rudder works differently from the oar because it does not strike the sea at right angles to its length, and it does not drive the ship forward, but turns it while it moves, receiving the sea at an angle. It is placed at the end and not in the middle of the ship because a moved body can move most easily when the moving power acts from the end. Baldi criticizes the relation between the movement of the oar and that of the rudder as established by the author of Mechanical Problems, who applies to the rudder the same argument used for the oar, putting the rowlock at the middle of the oar and considering the rowlock as moving along the oar. Baldi prefers to consider the sea as the fulcrum, and the rowlock or the hinge on which the rudder pivots as the weight. This explains why, when the ship is motionless, the rudder has no effect on the ship's movements to the left or to the right, whereas its effect is great when the ship is moving, because the movement of the ship at an angle is caused by the very movement of the sea which presses against the blade. The rudder works effectively only if it is positioned at an angle and the ship is moving.
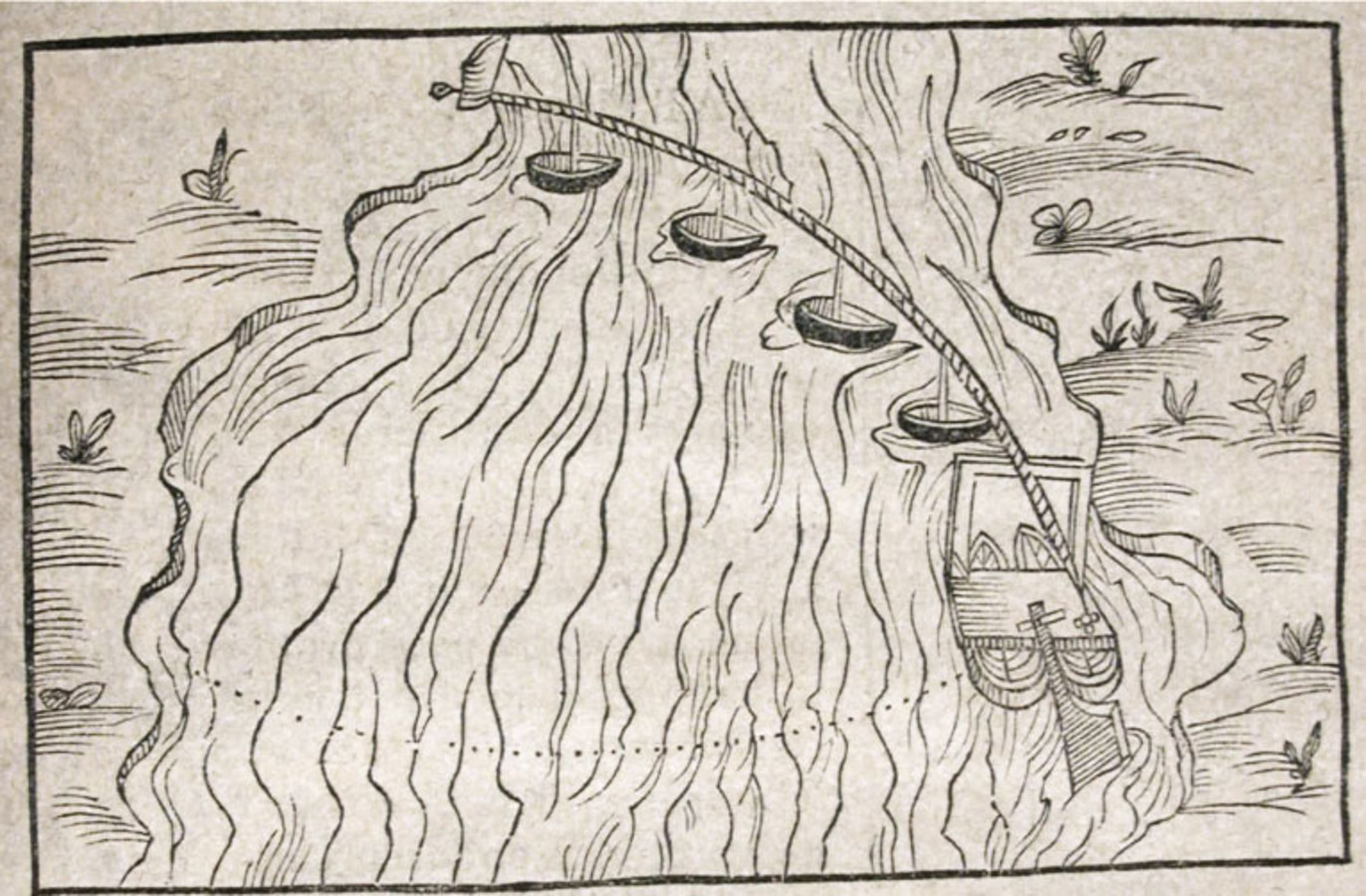
To make his point clear Baldi resorts to his personal observation of the way in which boatmen transport goods and people from one bank of a large river to the other. He describes the case of two pontoons joined by means of a plank, with the rudder placed between the two sterns, and the pontoons tied to a rope fixed to one of the banks. If the rudder is turned at an angle, its blade is pushed by the flowing water and drags the boat to the other bank. It is clear that the cause of this movement is not just the percussion of the water against the blade of the rudder, as Aristotle thought, but the pressure exerted by the flowing water upon the blade. The same explanation can be given for the sails of windmills which, by receiving wind at an angle, move the grindstones, and for the tails of birds and fish, which also function like rudders.
Question 6 asks why it is that the higher its yard-arm, the faster a ship moves, even though the sails and the wind are the same. The author of Mechanical Problems answers that this is because the mast acts as a lever and the fulcrum is where the mast is fixed, whereas the ship is the weight and the wind in the sails is the moving power. Baldi points out that, though it is true that the higher its yard-arm, the faster a ship moves, this causes at the same time a rising of the stern and a sinking of the prow. In fact, the kind of lever to be considered here is the bent lever, similar to that which operates in a pair of tongs for extracting nails, where the fulcrum is the joint. The mast of a ship, when bent by the wind, shifts and raises the weight of the ship. Since it is a bent lever, the power of the wind acting on the yard-arm is to the distance from the fulcrum as the distance from the fulcrum is to the weight of the ship. The center of gravity of the ship is placed toward the prow because of the arrangement of the cargo. As a consequence, the smaller the ratio between the two sides of the lever and the larger the weight, the less the power will prevail in raising the weight.
Question 7 asks why it is that when the sailors wish to sail before the wind, even if the wind is not blowing from the stern, they reef the sail in the direction of the helmsman and slacken the part of the sail toward the bows. The explanation given is that this happens because the rudder cannot act against the wind when it is strong, but it can when the wind is so light that they can catch it. Thus, the wind carries the ship forward, but the rudder forces it to blow from the stern, acting against the sea as a lever.
Baldi explains this short and obscure text by resorting to Piccolomini's commentary, where this case is reduced to that of a lever in which the wind is the weight, the rudder is the power, and the fulcrum is placed not at the middle of the ship, but toward the prow.19 Baldi however points out that this explanation raises the objection that the fulcrum should be steady, whereas here it is moving.
3.5 The Easy Movement of Bodies with Round Shapes: Question 8
In connection with the principle stated at the beginning of the work, Question 8 asks why round figures are the easiest to move. This problem gives Baldi the opportunity to make the first large digression. Aristotle distinguishes between three different types of circular motion: the motion of a circle on a plane, the motion of a circle around a fixed horizontal pivot, and the motion of a circle around a fixed vertical pivot. Baldi examines the following cases: the motion of a circle and an ellipse on a horizontal plane, the motion of a circle on an inclined plane, the impact of a wheel against an obstacle, and the motion on the bend of two wheels having the same axle. Then he discusses the problem of the motion of a cylinder and of a cone on a horizontal plane. The digression ends with an analysis of Aristotle's third type of rotating motion, that is, the motion of a circle around a vertical pivot. Baldi includes the case in which the axis of rotation is at an angle with the vertical line.
These cases are discussed in detail as follows: a circle or a sphere is at rest on a horizontal plane for the same reason that explains the equilibrium of a balance with equal arms loaded with equal weights. In a circle or sphere, the equal weights are the two equal parts of the figure on the right and on the left of the point of the plane on which they are standing and which acts as a fulcrum. Baldi makes the important observation that the motion on the horizontal plane is easiest because the center of gravity is neither raised in relation to the plane, nor with respect to the center of the earth. In the case of figures which are not circular, such as the ellipse, the center of gravity is raised and lowered during the motion on the horizontal plane. Furthermore, the effort made to push an ellipse forward is not constant, but changes constantly because the center of gravity goes up and down in varying ways. This happens also in the case of figures with sides such as polygons. In the case of the motion of a circle or sphere on an inclined plane, Baldi points out that the vertical line passing through the center of gravity of the figure does not go through the point of the plane on which the figure is placed, but further down, so that the figure is no longer supported by the plane, but rolls down the plane. In this case the two sides of the figure on the right and on the left of the point at which it touches the plane are not symmetrical. Baldi then shows that the equilibrium of a circle or sphere on an inclined plane is determined by the type of lever on which the weight of the figure, which is concentrated in the center of gravity, is placed between the fulcrum and the power that keeps the circle or sphere in equilibrium. He also shows that the smaller the angle of inclination of the plane, the less power is needed to keep the equilibrium. Baldi also mentions Pappus' Proposition 9 of Book Eight, which deals with the problem of determining the power needed to pull a weight up an inclined plane, but he does not discuss it since it was based on different hypotheses and arguments.20
Baldi questions why wheels with a larger diameter overcome an obstacle more easily than wheels with a shorter diameter. He presents two solutions to the problem, one based on the displacement of the center of gravity, the other on the law of the lever. The first solution shows that in overcoming the obstacle, the center of gravity of the two wheels are both raised to the same height, which is that of the obstacle; but the center of gravity of the larger wheel moves through a greater distance to reach the same height, so that the centers of gravity of the two wheels actually move on two different inclined planes, which have the same height but a different inclination. The second solution to the same problem shows that the two wheels can be considered as two levers of the second type, in which the weight is placed between the fulcrum and the power: the lever corresponding to the larger wheel needs less power than the lever corresponding to the smaller wheel.
Baldi then discusses the problem concerning the motion of two wheels with the same axle: when they turn, both wheels describe two concentric circular paths and the external wheel describes the circumference with a greater diameter, whereas the internal wheel could even remain at rest when it is at the center of the rotation. Baldi goes on to analyze the motion of a cylinder which rolls on a horizontal plane: if the bases of the cylinder are perpendicular to the axis, the cylinder moves in a straight line and describes two parallel lines; if the bases of the cylinder are not perpendicular to the axis and therefore elliptical, the lines described by the cylinder are still parallel, but curved rather than straight. Considering then the motion of a cone placed on a horizontal plane, Baldi shows that when the vertex remains in the same place, the lines traced by the points touching the plane are concentric circles. When the base of the cone is not perpendicular to the axis, Baldi wrongly believes that the line traced by the motion of the cone is an ellipsis.
Lastly, Baldi considers the case of a rotating motion around a vertical axis, such as the motion of a potter's lathe or the motion of a top. In this kind of motion the center of gravity remains still so that a small force is needed to start the motion and to keep it going, whereas the motion continues for a long time after the force has ceased to act. Baldi also points out that in this kind of motion the axis of rotation keeps its position unless an external cause interferes. Even when the axis of rotation is at an angle with the vertical line, it retains this position because the center of gravity moves neither up nor down. When the center of gravity is not on the axis of symmetry of a circular figure, during rotation it would not be at rest but would also be rotating and would move up and down: since the movement of the center of gravity upward is a violent motion, it would quickly stop.
3.6 The Simple Machines. The Axle in the Wheel, the Pulley and the Wedge: Questions 11, 13, 17–18
Though in the text of Mechanical Problems there is no mention of the axle in the wheel, Baldi discusses the properties of this machine in Question 13. By the end of his commentary on Question 11, he already briefly mentions an important aspect of the working of this machine. There the question was why heavy bodies are more easily carried on rollers than on chariots, though the latter have larger wheels than the former. Baldi agrees with Aristotle that the cause was the lack of friction in the case of rollers, whereas in the case of chariots there is the axle against which the wheels rub. He then adds that enormous weights are most effectively moved by means of rollers if levers are fixed to them, though in this case the resulting motion will be very slow. The slowness is compensated, however, by the ease in moving heavy loads. He gives a geometrical demonstration of this, but without relating it to the theory of the axle in the wheel. But in Question 13, he refers directly to this theory. In this question it is asked:
why are the longer bars (collopes) more easy to move round a spindle (iugum) than smaller ones; and likewise why are less bulky windlasses (suculae) more easily moved than thicker ones by the same force?21
Aristotle teaches that this is possible because both the spindle and the windlass are at the center, whereas the length of the bars sticking out from them represents the distance from the center, which is the radius. Now the radii of greater circles move more quickly and a greater distance is traversed by effect of the same force than the radii of smaller circles. In the case of less bulky windlasses, given an equal length of the bars, the part outside the wood is greater. After giving a geometrical demonstration of Aristotle's argument, Baldi explains the etymology of the Latin word sucula, meaning windlass, and adds that this was called axle in the wheel (axis in peritrochio) by the ancient writers on mechanics.22 Among the modern authors, Baldi mentions Guidobaldo del Monte who discusses this mechanical power in his Mechanicorum liber, where the functioning of this machine is explained on the basis of the principle of the lever.23
Question 17 asks: “why are great weights split by a small wedge, and why is great pressure exerted by it?” Aristotle and more recently Guidobaldo tried to reduce the wedge to the lever.24 Baldi declares that in order to find the true solution, he will not follow their opinion. But first he illustrates Aristotle's solution, showing that it is false and unworthy of such a great philosopher. He then mentions Guidobaldo's solution, which is certainly very clever but, in his opinion, presents a difficulty: he wrongly compares the wedge to an inclined plane. Baldi points out that when an inclined plane is reduced to the lever, the fulcrum is fixed, whereas in the case of the wedge reduced to the lever, the fulcrum continuously changes position.
Considering these difficult aspects of the problem, Baldi tries to explain the strength exerted by the wedge from a different point of view. He distinguishes two types of wedges: those that can be reduced to the nature of the line, and those that can be reduced to the nature of the surface. The former are shaped like lines ending in a point, such as needles, nails or daggers; the latter are made of two surfaces ending in a cutting line, such as knives, swords or axes. Baldi adds that wedges operate in two ways: either they are driven by a hammer, like axes, or they penetrate under the action of a push and under pressure, such as swords, daggers, chisels and awls, etc.
At the end of this chapter, Baldi analyzes the action of the lever in the act of splitting a thing with a wedge by considering the thing that is being split rather than the wedge itself. He shows that the fulcrum is continuously changing position so that the splitting becomes easier and easier. As a last case he analyzes the action of splitting a thing by means of a chisel used as a lever shaped like a wedge: the larger the ratio between the part of the chisel outside the split and the part inside it, the easier it is to split the thing.
The topics discussed in Question 18 are systems of pulleys and the ratio between power used and weight lifted. Baldi begins by quoting Aristotle's opinion according to which the greater the number of pulleys, the easier it is to lift weights. He corrects the way in which Aristotle had reduced the pulley to the lever and points out that the pulley is a lever with equal arms, which can be further reduced to a balance. On this basis, he rejects the Aristotelian statement that by augmenting the number of pulleys it would be easier to lift weights and shows that in a system of five pulleys the power applied is equal to the weight lifted. This is a system where the rope tied to the weight passes over fixed pulleys.25 In this system the force of the weight is not reduced, but power and weight are equal. Then Baldi argues that in a fixed pulley, power and weight are equal, whereas in a mobile pulley the power needed is half the weight. He shows how this principle works in a system of four pulleys by reducing it to four levers with equal arms, and calculates that a weight of 1000 librae is reduced 16 times so that the power needed to hold it would be a weight of 62.5 librae.26
3.7 The Sling: Question 12
The general problem of the motion of projectiles is discussed in Questions 32–34, whereas in Question 12 it is asked: “why are missiles thrown by a sling at a greater distance than those thrown by a hand?” Aristotle solves the question by saying:
perhaps this happens because the thrower hurls the missile which is already moved by the sling, since he throws it after swinging the sling round in a circle; but when projected from the hand it starts from rest. For everything is moved more easily when it is already set in motion than when it is at rest.
He adds moreover:
can it perhaps also be because in the case of the sling the hand becomes the center, and the sling the radius of the circular motion? Thus, the greater the radius, the faster the movement. But the circular movement made by throwing by hand is smaller than that made by the sling.27
Baldi approves Aristotle's solution, but adds more precisely that when the missile is thrown by the sling, the center of the circular motion is not the hand, but rather that part of the arm that is joined to the shoulder. He is also surprised that Aristotle did not notice that the thrower, in the very act of hurling, slowly rotates the sling around his head. He also adds that the speed of the missile is not acquired by just the rotation of the sling, but by the impetus generated in the very act of throwing the missile.
3.8 The Breaking and Deformation of Materials. Pieces of Wood and Pebbles: Questions 14–16
In Question 14 it is asked why the same piece of wood held at equal distances from the knee is more easily broken if one holds it far away from the knee than if one holds it quite close to it. The problem of the resistance to the breaking of a piece of wood is first discussed according to the law of the straight lever: the breaking depends on the greater or shorter distance of the point of application of the power from the fulcrum. To this obvious explanation Baldi adds another one, based on the law of the bent lever: one arm of the lever corresponds to the length of the piece of wood, the other arm to its thickness. This explains the importance of the ratio between the length and the thickness of a piece of wood in order to assess its resistance to breaking.28
Question 15 is the only one which is similar to a problem discussed in another work ascribed to Aristotle. Earlier, in Problemata (XXII, 36), it was asked why stones on the seashore become rounded. There, the answer does not refer to the circular figure. The explanation given by the author is based on the concept that the further an object is from the center, the more rapidly it moves. As a consequence, the parts further from the middle must be worn down and become rounded. Baldi points out that if it were a question of distance, the larger stones should be rounder than the smaller ones. But this is not the case. The problem is to be related to the natural brittleness of sharp edges and protuberances, which break easily so that the stones become smooth and rounded. As examples of the fragility of small projecting parts, he mentions the protruding parts of a statue (ears, nose, fingers, hands, feet), which can easily be broken, and the round shape of towers as well.29
Question 16 contains an important digression concerning the resistance of timbers and stone arches: Baldi's treatment of this subject is beyond comparison to previous studies of the matter. The Aristotelian text asks why pieces of timber are weaker and bend more easily the longer they are. After quoting the explanation of the author (based on a reasoning already described in the comment to Question 14), Baldi engages in a detailed analysis of the resistance of a rod (resistance of different materials such as glass, wood, steel) and of the different ways in which the breaking power operates (along the axis, as in the case of a column; or in a slanting or perpendicular direction). His analysis of the resistance to breaking is based on the law of the lever (which is already used in the comment to Question 14) and on the idea that in the case of the bending of a rod a rarefaction or condensation of matters occurs. Baldi is aware of the importance of this analysis for the art of building and devotes the rest of his commentary to a discussion of the way in which the principles of mechanics can be applied to the practical knowledge of architecture: he analyzes the resistance of floors, trusses, flat arches and vaults. By relating the resistance of a timber to static problems of more complex structures, Baldi aims to “make architects more prudent.”30
3.9 The Force of Percussion: Question 19
In Question 19 the author asks:
why, if one places a large axe on a block of wood and adds a large weight on top of it, does the axe not cut the wood to any extent; whereas if one strikes the wood after raising the axe, he splits it, even if the axe weighs much less than the weight that is placed on it and presses down on it?
He solves the question by saying:
it is because everything is produced by motion, and a heavy object acquires more motion due to its weight when it is moving than when it is at rest. When the weight lies on the wood, it does not move by effect of the motion, which is inherent to it by nature; but when it is already in motion, it is moved by effect of both this inherent motion and the motion of the striker.31
According to Baldi, what Aristotle has said up to here is brilliant; but what the philosopher adds concerning the operation of the axe acting like a wedge is refuted by him in Question 17. For Baldi the discussion of the effect of a blow with an axe must refer to the nature of falling bodies and of projectiles. He considers the example of a balance which is in equilibrium because it has equal heavy bodies lying on its scales: if other equal heavy bodies are added on both sides, the balance remains in equilibrium; but if one of these additional heavy bodies is dropped on one scale, this will cause it to go down. In the heavy body that is dropped there are two weights: one is its natural weight; the other is the weight that it acquires owing to this motion. If the additional heavy body were not just dropped, but thrown down, to its natural weight and to the weight acquired owing to its natural motion a third weight would be added, that is, the weight produced by the violence with which it is thrown.
Baldi then analyzes the circular motion of the axe during the act of striking, and the different weights that are produced in the different subsequent stages of that motion. Afterwards he points out the difference between splitting a piece of wood by striking it with an axe and splitting it by means of a wedge struck by a hammer. Finally, he discusses a “most beautiful question” (pulcherrima quaestio), that is, whether a blow from a sword is more effective near the tip or in the middle or near the hilt.
3.10 The Composition of Motions: Questions 23–24
At the beginning of Mechanical Problems Aristotle discusses the question of how two motions can produce a circular motion, and points out that this mixed motion can only be the result of two motions not having a constant ratio. He had previously shown that the composition of two motions having a constant ratio results in a diagonal of the figure generated by them. These arguments must have stimulated the author to reflect on the apparent paradoxes of mixed motions, which were later discussed in Questions 23 and 24. Before discussing Question 23, Baldi points out that this offers a splendid consideration concerning mixed motions, which were well known to the ancient authors on mechanics, as were curves such as spirals, helixes, cissoids, conchoids, etc., which they used to find the two mean proportionals (the duplication of the cube) and the squaring of the circle. The long text of the question reads:
why is it that in a rhombus, if the two extreme points move in two movements, they do not each pass through an equal straight line, but one passes through a much longer line than the other? In other words, why does the point that moves along the side pass through a distance less than the side? For one point goes through the diagonal, the other through the side which is longer, though the latter moves with one motion, and the other with two.32
How can the paradox be solved in which two points, which move with simple motions at equal speed, move through different distances? Aristotle concludes that one of the points moves with two motions, both of which are downward, whereas the other point moves with two motions, of which one is upward and the other downward; therefore the motion of the first point is faster and moves through a longer distance.
This solution seems not only to be true, but also marvellous and worthy of Aristotle. Baldi, however, shows that this is wrong and suggests another way of solving the paradox. In any parallelogram, including the rhombus, mixed motions, if they have the same proportion, are made along the diagonal. But the proportion between diagonals and sides is always changing, and therefore the proportions between the simple motions along the sides and the mixed motions along the diagonals will also always be changing. For instance, in the rhombus the mixed motions along the diagonals are not equal: the one along the greater diagonal is faster, and the one along the smaller diagonal is slower. Likewise, the simple motions of points along the sides are not equal to the motions along the diagonal.
Question 24 is one of the best known of the Mechanical Problems. Here it is asked: “why is it that a greater circle revolves along a line of the same length as a smaller circle when they are fixed around the same center?” When they revolve separately, then the lengths of the lines along which each of them revolves in turn are in the same ratio as their respective sizes. Since the geometrical figure used by Aristotle is somewhat obscure, Baldi proposes to demonstrate the same conclusion by using a clearer figure. Aristotle then explains the cause of such an amazing effect, after rejecting the opinion of those who think that the larger circle, when it is carried forward by the smaller circle, moves more slowly because it stops intermittently, whereas when the smaller circle is carried by the larger, it skips some space, so that the distances covered by the larger and by the smaller are the same. Before starting his demonstration, Aristotle assumes the following principles:
the same and equal force moves one mass more slowly and another more rapidly; if a body, which has a natural movement of its own, moves together with a body which has no natural movement of its own, it will move more slowly than if it moved by itself; but it will move more quickly if it moves without the other.33
Suppose that there are two bodies, one light, which has a natural movement upward, and the other one heavy, which has a natural movement downward. If the light body were linked together with the heavy one, it would be more difficult for it to move upward and it would move more slowly than if it moved detached from the heavy body.
Moreover, that which is moved not by its own movement, but by the movement of another body, must be moved just as far as the mover moves it. Therefore if the smaller circle is moved not by its own movement, but by the movement of the larger circle, it will cover a greater distance than if it moved by its own movement. Likewise, if the smaller circle revolves carrying the large one with it, the larger circle with its rotation will not cover a greater distance than that covered by the smaller circle.34
Aristotle says that those who think that each circle moves by itself when rotating around the same center are deceived. For when the smaller circle is carried by the larger one, the motion is made around the center of the larger circle; whereas if the larger circle is carried by the smaller, the motion is made around the center of the smaller. Aristotle's solution is considered by Baldi as absolutely certain and based on true causes.
3.11 The Construction of Beds: Question 25
In this question it is asked why beds are made with a length that is double the ends, and why the supporting ropes are not fixed diagonally? According to Aristotle, beds are probably made to those dimensions so that they may accommodate ordinary bodies: for the length is twice the width, the length being 4 cubits and the width 2 cubits. Baldi, however, remarks that in his time the proportion was 2 to 3, the length of the beds being 6 feet and the width 4 feet, so that a bed could accommodate two people. He also points out that the original text is rather obscure, both because its different readings in extant manuscripts are erroneous, and because Aristotle's argument is rather involute. Alessandro Piccolomini overcame this difficulty by using a text contained in a very ancient manuscript kept at the Marciana Library in Venice.35 The ancient author gives three explanations for the reason why the supporting ropes are not fixed diagonally: 1) because in this way the timbers to which they are fixed would be less strained; 2) because the ropes would be less strained if the weight is put on the ropes stretched crosswise rather than diagonally; 3) because fewer ropes would be needed. Concerning the first reason, Baldi shows the different ways in which the timbers are strained according to whether the ropes are fixed perpendicularly or diagonally. As to the second reason, he points out that the ropes fixed diagonally are longer and therefore less resistant than those fixed perpendicularly. As the third reason Baldi calculates the length of the ropes needed when they are fixed diagonally: for a bed 6 feet long and 3 feet wide, the rope needed is about 40 feet and 2/3; this result is slightly different from that given by Piccolomini, which is 40 and 1/2.36 Baldi is astonished that the ancients did not use the more simple perpendicular arrangement of ropes, which is more resistant and requires less rope, that is 32 feet, according to his own calculation.
3.12 The Placement of Weights Carried on the Shoulders: Questions 26–27, 29
In Questions 26 and 27, the problem of carrying weights on the shoulders of a single person is discussed, and in Question 29, the problem of a weight carried by two people. Why is it more difficult to carry a long timber on the shoulders at its ends than in the middle, though the weight is the same in both cases? In Question 26 Aristotle solves the problem by considering the vibration at the end of the timber and the lifting of the weight. Baldi points out that in the text it is not explained why the vibration interferes with the carrying, and he gives his own explanation by referring to the concept of center of gravity and to the idea of rarefaction and condensation of the timber carried on the shoulders, recalling what he had said concerning the breaking and the bending of materials in Question 16.
As to the role played by weight, the ancient author had remarked that a timber is more easily carried on the shoulders in the middle because in this case each of the two ends assists in lifting the other and raises the other in an upward direction. Baldi is not satisfied with this explanation and resorts to the Archimedean law of lever as defined by Guidobaldo in Proposition 3 of the treatise of the lever in his Mechanicorum liber.37 At the end of the Question, Baldi mentions similar problems, such as the difficulty of raising a rod by holding it at one end.
In Question 27 it is asked why it is that if the weight is extremely long, it is harder to raise it up onto the shoulders, even if it is carried in the middle, than if it were shorter. Baldi says that this question is similar to the previous one and can be criticized and explained in the same way.
The discussion of the way in which a weight is carried by two people in Question 29 is more interesting. It is asked why it is that when two people carry a weight between them by means of a timber placed at its ends on their shoulders, they feel a different pressure according to their distance from the weight; the closer the carrier is to the weight, the heavier it appears to be. For the author, the timber acts like a lever: the weight is the fulcrum, the carrier nearer to the weight is the thing that is moved, and the carrier more distant from the weight is the thing that moves. Therefore the more distant the moving carrier is from the weight, that is from the fulcrum, the greater the pressure is that is felt by the one moved at the shorter end of the timber. Baldi does not agree with this and referring to Piccolomini's Paraphrasis shows that there are two levers to be considered in one single timber.38 He argues that when the weight is placed at the middle of the lever, the carriers feel the same pressure, since the ratio of the length of the lever to each of its two parts is the same. At the end, Baldi discusses various cases: when the two carriers are of different height, when the weight does not hang freely from the lever, but is fixed to it so that its center of gravity changes position; and when the two carriers are of the same height but move on an inclined plane. The last case, Baldi points out, is similar to that of the wheelbarrow, which could be regarded as a lever with the weight placed between the fulcrum and the moving power.
3.13 Rising from a Sitting Position: Question 30
Question 30 asks:
why when men stand up, do they rise by making an acute angle between the shin-bone and the thigh-bone, and similarly between the trunk and the thigh-bone?
Aristotle answers that this is because equilibrium is a cause of rest and the right angle is an angle of rest and produces stability. When a man stands up his position is at right angles to the ground. When he is seated, his head and feet are not in a straight line, because the trunk is perpendicular to the thigh, as is the thigh to the lower leg. In this position he cannot rise. In order to rise he must bend the trunk and the lower leg so as to make an acute angle between them, and to bring his head immediately above his feet. Baldi rejects this solution to the problem, arguing that a man is unable to stand up from sitting, not because his position at right angles is a cause of stability, but because the center of gravity is outside the support of his feet and he is unable to lean against a stable point in the act of standing up. In order to stand up, it would be necessary to move the center of gravity so as to place it in one straight line, and this is exactly what happens by bending the trunk forward and the legs backward. In order to stand up, it is obvious that it is necessary to make acute angles, but this is not the cause of standing up, as Aristotle seems to think.
From his solution to the problem Baldi derives the solution to new questions: why the feet of men and of some animals who can walk in an upright position are not short and round, but rather long and extended in the lower part? Similarly, why are feet more extended toward the toes than toward the heel? Why those who walk on stilts keep upright by moving continually? All these questions Baldi answers by showing how, in order to keep in equilibrium, the center of gravity of both men and animals must fall inside that part of the body which makes it possible to stand up. The position of the center of gravity inside the supporting surface is a condition also for the equilibrium of objects made by man, such as vases, three-legged stools, etc. And this is the reason why the leaning towers in Pisa and in Bologna do not fall in spite of not being perpendicular to the ground.
3.14 Problems Concerning Motion: Questions 31–34
In Question 31 it is asked why it is easier to move that which is already moving than that which is stationary. Strictly speaking, this question is not mechanical since no machine is involved. Baldi gives the example of a sphere rolling on a plane by being pushed and points out that it is a physical problem. Baldi elaborates the solution given in Mechanical Problems: when a weight is moving in the opposite direction to the pusher, some of the power of the mover is lost; the same thing happens when the mover pushes a weight at rest. But when a body is already moving in the same direction as the pusher, it increases the force of the mover. This explanation, according to Baldi, offers a solution to the physical problem of why the speed of the natural motion of falling bodies increases continuously, and this constant push causes the acceleration of its motion.
Question 32 concerns the motion of projectiles and asks why thrown objects stop moving after a while. This, as well, is a physical problem. In Mechanical Problems various explanations are suggested, but Baldi accepts the solution given by Piccolomini in his Paraphrasis, which is based on the fact that the impressed force, by which the projectiles are moved, is not natural but accidental and violent, and as such does not last.39
Question 33 deals as well with the motion of projectiles and investigates why projectiles continue to move even after the thrower no longer has direct contact with the projectile. This is a central problem within the Aristotelian theory of violent motion. Once again Baldi's solution is in line with the explanation given by Piccolomini in his Paraphrasis of Mechanical Problems according to which the nature of the impressed motion is accidental and violent and eventually peters out. The last question concerning the motion of projectiles deals with a different aspect of the problem, that is, the proportion between the thrown body and the throwing force. Question 34 asks why neither small nor large bodies move very far when thrown, but must always bear a relation to the thrower. Baldi quotes the two explanations given in the Aristotelian work: it is either because an object thrown or pushed must always offer resistance to that which throws or pushes it; or because a moving body can only move as far as it can penetrate the depths of the air. Finally, Baldi deals briefly with three questions not strictly related to the main question: why does a body turn around when thrown so that its heavier part moves to the front? Why do pebbles skimmed across the surface of water rebound several times? Why does a ball thrown against an horizontal plane rebound at equal angles?
3.15 The Motion of Bodies in Eddying Water: Question 35
The last question of Mechanical Problems, like the four preceding questions, concerns the motion of bodies, but in contrast connects the problem with the properties of the circle. This question asks why objects which are moving in eddying water all end their movement in the middle. Aristotle explains that the moving object is moving in two circles, one lesser and one greater, and that the greater circle, because it is moving more quickly, is turning the object around and driving it sideways into the smaller circle. Driven then from the second circle into the next inner circle and so on, the moving object ultimately reaches the middle and remains there at rest. In addition, the weight of the object overcomes the speed of the revolving circle so that it is left behind in each lesser circle in succession until it arrives at the center.
Baldi, however, does not accept Aristotle's explanation, as brilliant as it may be, and points out that whirlpools are not circles turning around the same center, but rather rotating movements along a spiral. In addition, the weight of the moving object could only cause its motion to slow down, but the movement toward the center must have a different cause.
3.16 Appendix: The Problem of the Two Mean Proportionals
At the end of Baldi's commentary to the Mechanical Problems there is an Appendix which does not seem related to the questions discussed in the Aristotelian text. It is a classical problem from ancient mathematics: finding two mean proportionals between two given straight lines. Baldi, after mentioning the solutions given by ancient mathematicians, suggests a mechanical procedure for finding a solution, claiming its originality. The demonstration of the validity of Baldi's solution is based on the ancient demonstration produced by Pappus for a procedure suggested by Nicomede.40
Footnotes
This part of the introduction benefits from the Italian translation and commentaries of Baldi's Exercitationes undertaken in Milan from 2006–2008 by a research team comprising Sergio Aprosio, Antonio Becchi, Adriano Carugo, Ferruccio Franco Repellini, Enrico Gamba, Romano Gatto, Gianni Micheli and Elio Nenci. See Baldi 2010.
The manuscripts of Dissertationes and Exercitationes were previously kept at the library of the Accademia Toscana di Scienze e Lettere La Colombaria, but were destroyed during World War II. Some interesting notes on mechanics related to the topics discussed in Exercitationes are extant (ms XIII.F.25, 129r–136r) in the National Library in Naples. They are now being studied by Antonio Becchi.
In a letter addressed to Pier Matteo Giordani on November 17, 1614, Baldi wrote: “I shall bring with me the original text of my work on mechanics so that we can look at it together” (Oliveriana Library in Pesaro, Cod, 430, 59).
On September 3, 1615 Baldi wrote to Johann Faber asking for his help in recovering the work that had been sent to Germany. See Serrai 2002, 111–112, 142.
See the figure in Baldi 1621, 3.
The assumption that larger balances are more accurate than smaller ones had already been criticized by Tartaglia in Book Seven of his Quesiti et inventioni diverse, 1546.
This fact had already been remarked by Tartaglia, who in Book Eight of his Quesiti et inventioni diverse explains the equilibrium of a balance with its support at the center of gravity on the basis of the principles of the medieval science of weights.
This machine is made of a long beam pivoting on top of another beam vertically driven into the ground: the bucket hangs from one end of the pivoting beam, whereas a load or stone is attached to the other.
For a discussion of Questions 14 and 16, see Becchi 2004 and Valleriani 2009.
See Becchi 2004.