The late 1940s saw the solution of the divergence difficulties of quantum field theory, or at least quantum electrodynamics.1 The renormalization program was successful not only in removing the infinities, but also in giving precise values to the finite remainders. These were in excellent agreement with newly discovered precision effects, such as the Lamb shift and the anomalous magnetic moment of the electron. The renormalization techniques were, at least initially, based on the covariant quantization procedure discussed in Chapter 17 and their application to the quantization of gravity was taken up in the 1950s.
In parallel, and sometimes in direct opposition, to the development of renormalized quantum field theory (QFT), a second route to quantum gravity was developed in the late 1940s, initially by Peter Bergmann. Bergmann had been an assistant of Einstein from 1936 to 1941 and had worked with Einstein on the attempts to construct a five-dimensional unified field theory (UFT).2 But unlike Einstein, Bergmann was not in radical opposition to modern quantum theory, having learned it as a student of Philipp Frank in Prague in the mid-1930s. After obtaining a permanent position at Syracuse University, Bergmann thus abandoned the pursuit of a unified field theory and set himself to reconcile general relativity (GR) and quantum theory through the construction of a quantum theory of gravity.
Bergmann was little concerned with the contemporary rapid development of renormalized quantum field theory. And indeed, the covariant QED of the day did not seem to harmonize well with his vision of quantum gravity. The QED of Schwinger was construed as the quantization of free, linear field theories, both for matter and the electromagnetic field, which were then perturbed by the introduction of interactions between the fields, leading to the non-trivial time evolution of the quantum state in the interaction picture.
But for Bergmann the essential element of GR was its non-linearity, because it made possible the derivation of the equations of motion of point particles directly from the field equations, as outlined by Einstein, Infeld and Hoffmann (EIH) during Bergmann’s time with Einstein. Bergmann’s hope was that this feature would carry over from the classical to the quantum theory, so that a quantum theory of gravity would directly lead to the quantum equations of motion of point particles as well. He was thus envisioning not merely an appropriation of the field theory of general relativity through quantum theory by the methods of field quantization, but rather a true marriage between general relativity and quantum theory, where the introduction of general relativity would help to solve the divergence difficulties of quantum field theory, which he, like many others, saw as originating from the difficulties of having point-like particles.
Of course this approach was not entirely up to date with the current state of quantum field theory, which had in a sense dispensed with the quantum mechanical notion of in principle localizable, point-like entities. Photons were certainly not perfectly localizable, nor were charged particles in electron-positron theory. And Bergmann had to admit that already classically the EIH procedure was only feasible if one disregarded splitting world lines, as in the emission of a photon or electron-positron pair creation. But these difficulties were put aside for the moment. Bergmann was after a quantum theory of point particles and the gravitational field.
The predilection for the EIH procedure was not the only inheritance from Bergmann’s time with Einstein. From his work on UFT, he also had a clear understanding that GR was not to be considered the final field theory of gravitation. In his program, he thus did not engage directly with GR and the quantization of the space-time metric, but preferred to discuss the quantization of a more general field theory that kept what he considered to be the essential elements of GR: general covariance and non-linearity, which together ensured the feasibility of the EIH-type determination of particle trajectories.
The study of the quantization of a field theory mainly characterized by its invariance properties unwittingly brought him very close to Rosenfeld’s first 1930 paper on what we have called the momentum difficulty. And indeed, in his first paper on the subject (Chapter 32), Bergmann showed not only that a general non-linear, generally covariant field theory would have all the attractive features of GR (EIH determination of the equations of motion, as well as energy conservation, at least in the same sense as in GR), but would also lead to identities involving the canonical momenta, of the type that Rosenfeld had first discovered. There are slight differences in the treatment, of course: Bergmann did not consider spinorial matter and thus did not introduce tetrads or local Lorentz symmetry.3 Without tetrads, even for the case of regular general relativity, Bergmann could not have constructed a Lagrangian that both contained only first-order derivatives of the field (metric) quantities and was at the same time a scalar. He thus treated a more general case than Rosenfeld’s, allowing for the Lagrangian to change by a total divergence under a general coordinate transformation.4 Bergmann’s derivation of the constraints was thus somewhat different from Rosenfeld’s and went via the (generalized) contracted Bianchi identities. This actually lent a certain degree of coherence to Bergmann’s overall approach, as the Bianchi identities also played an essential role in the generalized derivation of the EIH result.
Bergmann identified the identities (and the non-unique time development they implied) as the central challenge for the quantization of a generally covariant field theory. He was well aware that this problem could be remedied by the imposition of gauge, or rather, in this case, coordinate conditions, but general covariance was such a central concept to him that he instead aimed for constructing a Hamiltonian in which the arbitrariness of coordinate choice showed up explicitly, in the form of four arbitrary functions. He was thus aiming for a quantization procedure very alike that of Rosenfeld, yet without, it should be pointed out, being aware of Rosenfeld’s work.
The second paper he published in that same year, together with his colleague Johanna Brunings, represented a further step towards quantization (Chapter 33). The central point Bergmann wanted to address here was how to carry over the EIH method into quantum theory. The difficulty he had to address was the following: If there are singular worldlines in space-time, where the field equations are not satisfied, then one should not integrate over these singular regions in the action integral, whose minimization gives the field equations. However, without first solving the field equations, one cannot know the exact singular particle trajectories. Bergmann’s solution was the “parameter formalism.” The idea was that since the spacetime trajectories of the singularities could not be known in advance, a four-dimensional multiply connected parameter space
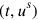 could be utilized in which parameter tubes could be excised without making a commitment as to the corresponding spacetime particle paths. The original spacetime coordinates
could be utilized in which parameter tubes could be excised without making a commitment as to the corresponding spacetime particle paths. The original spacetime coordinates
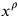 were taken to be functions of these parameters, thus becoming field variables on par with the gravitational field, dynamical equations of motion and all. The introduction of parameters was, as acknowledged by Bergmann, closely related to Weiss’s approach discussed in Chapter 17: For Weiss, too, the field variables were no longer functions of the space-time coordinates, but rather of the parameters defining a point on the hypersurface, as well as of a further parameter (
were taken to be functions of these parameters, thus becoming field variables on par with the gravitational field, dynamical equations of motion and all. The introduction of parameters was, as acknowledged by Bergmann, closely related to Weiss’s approach discussed in Chapter 17: For Weiss, too, the field variables were no longer functions of the space-time coordinates, but rather of the parameters defining a point on the hypersurface, as well as of a further parameter (
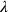 in Weiss’s notation,
in Weiss’s notation,
 in Bergmann’s), labelling a member of a sequence of hypersurfaces. And for Weiss the original space-time coordinates were also functions of the parameters. However, in Weiss’s case this was merely to be understood as the definition of a specific foliation of space-time. As Bergmann pointed out, the emergence of the original coordinates as dynamical variables on the same footing as the field variables
in Bergmann’s), labelling a member of a sequence of hypersurfaces. And for Weiss the original space-time coordinates were also functions of the parameters. However, in Weiss’s case this was merely to be understood as the definition of a specific foliation of space-time. As Bergmann pointed out, the emergence of the original coordinates as dynamical variables on the same footing as the field variables
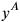 , which was the essential point for Bergmann, was not discussed by Weiss, who consequently also did not investigate the momenta canonically conjugate to the original coordinates.
, which was the essential point for Bergmann, was not discussed by Weiss, who consequently also did not investigate the momenta canonically conjugate to the original coordinates.
Bergmann’s parameter formalism was now covariant not just under coordinate transformations but also under arbitrary reparameterizations. This covariance brought with it four new identities. Three of these (corresponding to the three spatial parameters
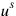 ) could be straightforwardly deduced from the definition of the new canonical momenta conjugate to the now-dynamical spacetime coordinates. Repeating this procedure for the fourth (time) parameter
) could be straightforwardly deduced from the definition of the new canonical momenta conjugate to the now-dynamical spacetime coordinates. Repeating this procedure for the fourth (time) parameter
 , did not directly deliver another constraint. Instead, Bergmann could show in this manner that the Lagrangian in the parameter formalism was homogeneous of degree one, in both the field velocities
, did not directly deliver another constraint. Instead, Bergmann could show in this manner that the Lagrangian in the parameter formalism was homogeneous of degree one, in both the field velocities
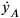 and the coordinate velocities
and the coordinate velocities
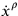 , where the dot refers to differentiation with respect to parameter time
, where the dot refers to differentiation with respect to parameter time 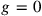 could be deduced.
could be deduced.
This function
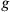 had the properties of the Hamiltonian density, that is, it generated the canonical field equations of motion through functional differentiation. Consequently, using Poisson brackets (in the parameter version, first introduced by Weiss in the 1930s, but now, in Bergmann and Brunings’ approach, also including the space-time coordinates as dynamical variables) the spatial integral of
had the properties of the Hamiltonian density, that is, it generated the canonical field equations of motion through functional differentiation. Consequently, using Poisson brackets (in the parameter version, first introduced by Weiss in the 1930s, but now, in Bergmann and Brunings’ approach, also including the space-time coordinates as dynamical variables) the spatial integral of
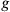 (the Hamiltonian) could be used to determine the time derivative of some functional of the canonical variables.5 They then claimed to show, by calculating the Poisson bracket of the Hamiltonian with an arbitrary linear combination of the constraints, that all eight constraints had vanishing time derivatives, and that consequently no further constraints had to be considered. As Bergmann himself would soon realize, this proof was fallacious.6 They also outlined how to proceed to a quantum theory, in the same manner proposed by Rosenfeld, that is, by turning the Poisson brackets into commutators and the constraints into auxiliary conditions on the wave function.
(the Hamiltonian) could be used to determine the time derivative of some functional of the canonical variables.5 They then claimed to show, by calculating the Poisson bracket of the Hamiltonian with an arbitrary linear combination of the constraints, that all eight constraints had vanishing time derivatives, and that consequently no further constraints had to be considered. As Bergmann himself would soon realize, this proof was fallacious.6 They also outlined how to proceed to a quantum theory, in the same manner proposed by Rosenfeld, that is, by turning the Poisson brackets into commutators and the constraints into auxiliary conditions on the wave function.
But although several important properties of the constraint
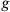 were known, Bergmann and Brunings did not provide a method for explicitly constructing it. They could show that it was not unique: For example, if one added to
were known, Bergmann and Brunings did not provide a method for explicitly constructing it. They could show that it was not unique: For example, if one added to
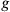 some linear combination of the remaining seven constraints, the resulting function would of course still be a constraint and could also still be taken as a Hamiltonian density, the new canonical field equations of motion being related to the ones of the original
some linear combination of the remaining seven constraints, the resulting function would of course still be a constraint and could also still be taken as a Hamiltonian density, the new canonical field equations of motion being related to the ones of the original
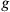 by a suitable canonical transformation of the dynamical variables along with a transformation of the space-time parameters. This implied that some specific choice of Hamiltonian density corresponded to choosing a coordinate condition and thus losing general covariance. But Bergmann and Brunings neither showed how to construct a specific Hamiltonian, corresponding to a particular coordinate condition, nor a general Hamiltonian involving arbitrary functions. They thus had reached, in 1949, about the same point that Rosenfeld had reached in 1930. The next step was clearly the explicit construction of a Hamiltonian, only that now, in Bergmann’s parameterized approach, this Hamiltonian would not just generate the field equations of motion and time evolution of physical variables, but would also itself be one of the constraints.7
by a suitable canonical transformation of the dynamical variables along with a transformation of the space-time parameters. This implied that some specific choice of Hamiltonian density corresponded to choosing a coordinate condition and thus losing general covariance. But Bergmann and Brunings neither showed how to construct a specific Hamiltonian, corresponding to a particular coordinate condition, nor a general Hamiltonian involving arbitrary functions. They thus had reached, in 1949, about the same point that Rosenfeld had reached in 1930. The next step was clearly the explicit construction of a Hamiltonian, only that now, in Bergmann’s parameterized approach, this Hamiltonian would not just generate the field equations of motion and time evolution of physical variables, but would also itself be one of the constraints.7
In reaching this next step, Bergmann’s group was beaten by Felix Pirani and Alfred Schild. Their work built on an approach to constrained Hamiltonian dynamics quite different from that of Rosenfeld or Bergmann, presented by Paul Dirac in August/September 1949 at the Summer Seminar of the Canadian Mathematical Congress (Chapter 34), a newly established graduate-level summer school, which in that year (its second installment) had a special focus on mathematical physics, other lecturers including Homi J. Bhabha (on quantum field theory) and Laurent Schwartz (on distribution theory; Proceedings of the Second Canadian Mathematical Congress 1951). Dirac came to constrained Hamiltonian dynamics from a direction quite different from that of Rosenfeld or Bergmann. He was not interested in the effect of symmetries when passing from a Lagrangian to a Hamiltonian formulation of a field theory, be they general local symmetries (Rosenfeld) or general covariance in particular (Bergmann). Dirac’s focus was rather a subject that had been on his mind for quite some time: The relation between Hamiltonian dynamics and special relativity. Dirac viewed this as the central problem in constructing a (special) relativistic quantum (field) theory, a problem he still considered to be wide open, as he was not particularly inclined towards the renormalization methods being developed at the time.8 He had already remarked in 1933:
Quantum mechanics was built up on a foundation of analogy with the Hamiltonian theory of classical mechanics. This is because the classical notion of canonical coordinates and momenta was found to be one with a very simple quantum analogue, as a result of which the whole of the classical Hamiltonian theory, which is just a structure built up on this notion, could be taken over in all its details into quantum mechanics. [...] [T]he Hamiltonian method is essentially non-relativistic in form, since it marks out a particular time variable as the canonical conjugate of the Hamiltonian function. (Dirac 1933b, 64.)
At the time, Dirac had believed that the way to proceed towards a relativistic quantum theory was consequently to find a new quantization procedure based on the classical Lagrangian, instead of the classical Hamiltonian, formalism. This was based on the realization that the action function appearing in the Lagrangian formalism, that is, the time integral of the Lagrangian itself, is a relativistic invariant. 16 years later, however, Dirac was considerably more optimistic about the reconcilability of Hamiltonian dynamics and relativity. The main reason for this appears to have been Dirac’s adoption of Weiss’s parameter formalism, which had been devised by Weiss precisely in order to obtain a covariant generalization of classical Hamiltonian dynamics, including canonical variables and Poisson brackets, as a starting point for the quantization of relativistic field theories.
In his Canadian lectures, Dirac went significantly beyond Weiss. Dirac emphasized that the parameter approach would turn the original space-time coordinates into dynamical variables in their own right. This came from a long tradition in Dirac’s thinking: Already in the mid-1920s (Dirac 1926), and then again in 1933 (Dirac 1933a), Dirac had explored the possibility of turning time from an evolutionary parameter into a dynamical variable in relativistic particle mechanics, an approach which is the particle-mechanical analog of the field-theoretical parameter formalism. As opposed to Bergmann, however, Dirac did not place any physical expectations in the newly dynamical nature of the coordinates: To him, this was merely a mathematical observation, one that ensured the (Lorentz) covariance of the scheme. In his 1949 lectures, Dirac further recognized that the use of the parameter formalism would imply the existence of constraints, including the Hamiltonian constraint, another insight going back to his early particle-mechanical exploration of the subject. This helped explain how the dilemma in the above quote was solved: The parameter formalism allowed a separation between (a) the Hamiltonian function giving the total energy or energy density (which now appeared as one canonical momentum among others, conjugate to the dynamical time coordinate) and (b) the generator of the equations of motion and the time evolution of physical quantities (which was now the task of the constraints, or, as Dirac had called them in 1933, the Hamiltonian equations).
It was on this basis that Dirac built up his approach to constrained dynamics. The structure he obtained was general enough to also accommodate constraints that did not arise from the use of parameters (and also to deal with a non-parameterized theory, involving only other constraints). Dirac mentioned this fact, even though he did not refer to any examples (back in 1933, however, he had mentioned the analogy with the constraints arising in electrodynamics), but Pirani and Schild, who were attending the conference, quickly picked up on the applicability of Dirac’s approach to General Relativity. Still, it should be emphasized that to Dirac the constraints arising from the parameters were the essential ones; additional constraints could simply be added on, as further identically fulfilled relations between canonical coordinates and momenta. Where these additional constraints might come from was of no concern to Dirac at the time and he did not discuss symmetry properties at all.9 This of course made Dirac’s constrained dynamics look quite different from that of Bergmann, and one might spend a whole paper discussing the differences and similarities between the two. In the following, we will just briefly focus on the specific difference that was important for the work of Pirani and Schild, namely, that Dirac’s formalism provided an explicit construction principle for the Hamiltonian.
In working out the properties of their constraint
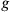 , Bergmann and Brunings had, quite naturally, considered it to be a function of canonical coordinates and momenta only, allowing for derivatives of the canonical coordinates with respect to the spatial parameters
, Bergmann and Brunings had, quite naturally, considered it to be a function of canonical coordinates and momenta only, allowing for derivatives of the canonical coordinates with respect to the spatial parameters
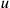 , but not allowing for velocities, that is, derivatives of the canonical coordinates with respect to the time parameter
, but not allowing for velocities, that is, derivatives of the canonical coordinates with respect to the time parameter
 . However, the Hamiltonian density
. However, the Hamiltonian density
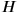 is quite easily written down as a function of canonical coordinates, momenta, and velocities as
is quite easily written down as a function of canonical coordinates, momenta, and velocities as
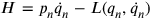
|
31.1 |
using Dirac’s notation, where the
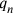 are all the canonical coordinates (including the original space-time coordinates), the
are all the canonical coordinates (including the original space-time coordinates), the
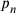 are the conjugate momenta and the dot denotes differentiation with respect to the time parameter
are the conjugate momenta and the dot denotes differentiation with respect to the time parameter
 . Now normally this is just an intermediate step in constructing the canonical Hamiltonian, the next step being the elimination of the velocities with the help of the defining equations for the momentum. This is, however, as we have already remarked in context of Rosenfeld’s work in Chapter 17, a non-trivial task. It was now Dirac’s innovation to consider Equation 31.1 not as an intermediate step—basically just a construction prescription—but rather as an actual expression for the Hamiltonian defined not on the usual phase space, but rather on a larger, 3
. Now normally this is just an intermediate step in constructing the canonical Hamiltonian, the next step being the elimination of the velocities with the help of the defining equations for the momentum. This is, however, as we have already remarked in context of Rosenfeld’s work in Chapter 17, a non-trivial task. It was now Dirac’s innovation to consider Equation 31.1 not as an intermediate step—basically just a construction prescription—but rather as an actual expression for the Hamiltonian defined not on the usual phase space, but rather on a larger, 3
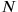 -dimensional (with
-dimensional (with
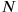 the number of configuration variables) space, which also included the
the number of configuration variables) space, which also included the
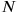 velocities as independent variables. The usual Hamiltonian was then obtained by going to a 2
velocities as independent variables. The usual Hamiltonian was then obtained by going to a 2
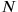 -dimensional subspace, where all the defining equations for the momenta (including primary constraints) were fulfilled (this subspace of course corresponds to usual phase space if there are no constraints).
-dimensional subspace, where all the defining equations for the momenta (including primary constraints) were fulfilled (this subspace of course corresponds to usual phase space if there are no constraints).
Dirac was now able to find another expression for the Hamiltonian density as a function of coordinates, momenta, and velocities:
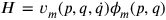
|
31.2 |
where the
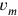 are some suitable functions, the important thing being that out of each summand one of the constraints
are some suitable functions, the important thing being that out of each summand one of the constraints
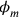 (the summation over
(the summation over
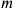 is over all constraints, those arising from parameterization and those intrinsic to the theory) can be factored out, the constraint being a function of coordinates and momenta alone.
is over all constraints, those arising from parameterization and those intrinsic to the theory) can be factored out, the constraint being a function of coordinates and momenta alone.
Pirani and Schild, both in Toronto at the time, Schild working with Leopold Infeld and Pirani just having acquired his Master’s degree, attended Dirac’s Vancouver lectures in 1949. According to Pirani’s recollections,10 Schild immediately realized the applicability of Dirac’s method to the quantization of general relativity.11 Indeed, the paper of Bergmann and Brunings had appeared just a month before Dirac’s lecture, and it is quite probable that Schild had seen it and then in Vancouver realized how Dirac’s method might supply the Hamiltonian and the eighth constraint. He discussed the matter with Pirani, who promptly agreed to go with him to Pittsburgh (where Schild had just accepted a job at the Carnegie Institute of Technology) and become Schild’s first PhD student, the subject of his thesis being the quantization of general relativity. Pirani’s thesis (Pirani 1951) (which dealt, among other things, also with the inclusion of fermionic spinors) was not completed until 1951, but Pirani and Schild had already presented first results at the APS Meeting in New York (February 2–4, 1950, Schild and Pirani 1950) and submitted the paper reprinted here in Chapter 35 on February 14. By comparing the two forms of the Hamiltonian provided by Dirac, they were quite easily able to construct the first Hamiltonian for parameterized GR and thereby to also explicitly identify the eight primary constraints. Bergmann and his group were not far behind and published their Hamiltonian within the same year, constructed using a different procedure based on finding the “quasi-inverse” of the singular Legendre matrix (Bergmann et al. 1950).12
The success of Pirani and Schild and the Bergmann group in constructing a Hamiltonian for GR was initially seen as invalidating an approach based on the notion of a free graviton field, perturbed by its self-interaction and its interactions with other fields. Such an attempt at quantizing gravity had been worked out in the 1949 PhD thesis of Bryce DeWitt (né Seligman), a student of Schwinger’s, using the newly developed covariant techniques of his supervisor (DeWitt 1949). DeWitt wrote up a paper based on his thesis13 in 1950 in which he duly acknowledged “the rigorous Pirani-Schild-Dirac scheme,” having been able to read a manuscript of the Pirani-Schild paper before publication. Still, DeWitt’s paper, which he submitted to the Physical Review, was essentially rejected by the referee, H. P. Robertson. In his referee report,14 he stated
In view of the Pirani-Schild paper, which Seligman has seen—and remarks on p. 3, footnote, that this should eventually be carried out in terms of their more rigorous theory—it would seem to me better to suggest he carry out his work in terms of their theory.
DeWitt’s thesis work was never published, and he indeed turned to working on the Pirani-Schild formulation soon after (DeWitt 1952;DeWitt and DeWitt-Morette 1952).
However, as it turned out, the gravitational Hamiltonians of 1950 were not the last word on quantum gravity, with only details left to be filled out. The most immediate foundational reform was the abandonment of the parameter formalism by both groups within the same year. For Bergmann the parameter formalism had carried the hope of a quantum version of EIH, in which the space-time coordinates, which were dynamical variables in the parameter formalism, could be interpreted as the coordinates of a quantum mechanical point particle. That this will not work is rather obvious from a modern perspective: The parameterization introduces four additional constraints which reduce the number of dynamical degrees of freedom by exactly the number of dynamical variables one had formally gained by introducing the parameters in first place. But recall that Bergmann and Brunings had originally convinced themselves that there were no secondary constraints in their formalism; they were simply ignoring four of the constraints actually present in the formalism. And indeed, Bergmann’s abandonment of the parameter formalism appears to coincide with his realization that there were in fact additional secondary constraints.
In an interview, Joshua Goldberg placed the abandonment of the parameter formalism in the summer of 1950 or 1951,15 with the published evidence clearly favoring the former (the first parameter-free paper by the Bergmann group was already submitted in May 1951, see Anderson and P. G. Bergmann (1951)). And in a short note to Schild, dated 16 November 1950,16 Bergmann announced that his group had discovered additional constraints (i.e., had discovered the secondary constraints) and was working on a proof that there were as many additional constraints as there were primary ones. Such a proof was supplied a year later in the non-parameterized formalism (Anderson and Bergmann 1951), and really only makes sense therein, as there are more primary than secondary constraints in the parameter formalism. So there is strong circumstantial evidence that Bergmann’s abandonment of the parameter formalism was closely linked with the discovery of the secondary constraints, even though Bergmann never made that point explicitly in writing. In fact, he never even retracted his “no secondaries” argument in his published work. In the first detailed, published presentation of the parameter-free formalism (Penfield 1951), the new approach was merely presented as equivalent to the parameter formalism (for singularity-free gravitational fields), the manifest covariance of the latter thus ensuring the covariance of the former. And only another two years later, after the question of which were to be the actual physical observables in a constrained theory moved to the center of Bergmann’s attention, did he go on record stating that the parameterization did not, as he had hoped, introduce new observables (i.e., particle trajectories) into the theory (Bergmann and Schiller 1953).
The idea of introducing particle trajectories as new quantum operators via parameterization had never played a prominent role for Pirani and Schild. Parameterization had rather been a means (inherited from Dirac) for making the general covariance of the setup manifest, as it allowed for a definition of (parameter) time that did not presuppose any metric structure for space-time (which of course was to be a result of the field equations), but could be defined solely through the introduction of a family of three-dimensional hypersurfaces in the metric-free (Pirani used the term “amorphous” in his thesis) parameter space. When Schild received the above-mentioned note by Bergmann in November 1950, he had not yet considered abandoning parameters.17 He and Pirani had (probably following Bergmann and Brunings) been convinced that there were no secondary constraints, without providing any argument for this statement. After receiving Bergmann’s note, Pirani attempted to calculate the secondary constraints in the parameterized formalism. This proved to be a formidable task, too formidable indeed: Pirani, in his thesis, merely presented some preliminary calculations in this direction, stating (p. 42) that “[t]he long and complicated expressions which make their appearances [...] led to a search for some way of simplifying the theory.” Pirani and Schild thus followed the lead of the Bergmann group, dropping the parameters, merely viewing them as a proof of the general covariance of the Hamiltonian formulation (Pirani 1951).18
Later work on the canonical quantization of gravity thus looked quite different from that done in these early works of 1949/50. In particular, as pointed out by Pirani to Schild in a letter from 4 December 1952,19 the problem of integrating over singular regions in the action integral, which Bergmann had avoided by introducing parameters, remained. Indeed the parameter-free formalism strongly implied entirely doing away with the idea of particles as singularities (and thus the whole quantum EIH approach), and instead adopting more modern, (quantum) field-theoretical descriptions of matter. Still, this early work provided a basis for all later attempts at canonical quantization, introducing most of the concepts and terminology regarding the appearance of constraints.
References
Anderson, James L., and Peter G. Bergmann (1951). “Constraints in Covariant Field Theories.” Physical Review 83: 1018–25.
Bergmann, Peter G., Robert Penfield, Ralph Schiller, and Henry Zatzkis (1950). “The Hamiltonian of the General Theory of Relativity with Electromagnetic Field.” Physical Review 80: 81–88.
Bergmann, Peter G., and Ralph Schiller (1953). “Classical and Quantum Field Theories in the Lagrangian Formalism.” Physical Review 89: 4–16.
DeWitt, Bryce (1949). “I: The Theory of Gravitational Interactions. II: The Interaction of Gravitation with Light.” PhD thesis, Harvard.
——— (1952). “Point Transformations in Quantum Mechanics.” Physical Review 85: 653–61.
DeWitt, Bryce, and Cécile DeWitt-Morette (1952). “The Quantum Theory of Interacting Gravitational and Spinor Fields.” Physical Review 87: 116–22.
Dirac, Paul A. M. (1926). “Relativity Quantum Mechanics with an Application to Compton Scattering.” Proceedings of the Royal Society, Series A 111 (758): 405–23.
——— (1933a). “Homogeneous Variables in Classical Dynamics.” Mathematical Proceedings of the Cambridge Philosophical Society 29: 389–400.
——— (1933b). “The Lagrangian in Quantum Mechanics.” Physikalische Zeitschrift Der Sowjetunion 3 (1): 64–72.
Einstein, Albert (1916). “Die Grundlage Der Allgemeinen Relativitätstheorie.” Annalen Der Physik 49: 769–822.
Goldberg, Joshua (2005). “Syracuse: 1949–1952.” In Einstein Studies Volume 11: The Universe of General Relativity, edited by A. J. Kox and Jean Eisenstaedt, 357–71. Basel: Birkhäuser.
Halpern, Paul (2005). “Peter Bergmann: The Education of a Physicist.” Physics in Perspective 7: 390–403.
Kragh, Helge (1990). Dirac: A Scientific Biography. Cambridge: Cambridge University Press.
Penfield, Robert (1951). “Hamiltonians Without Parameterization.” Physical Review 84: 737–43.
Pirani, Felix A. E. (1951). “On the Quantization of the Gravitational Field of General Relativity.” PhD thesis, Carnegie Institute of Technology.
Pitts, J. Brian (2014). “Change in Hamiltonian General Relativity from the Lack of a Time-Like Killing Vector Field.” Studies in History and Philosophy of Modern Physics 47: 68–89.
Proceedings of the Second Canadian Mathematical Congress (1951). Toronto: University of Toronto Press.
Rao, C. Radhakrishna, and Sujit Kumar Mitra (1971). Generalized Inverse of Matrices and Its Applications. New York: Wiley.
Salisbury, Donald (2006). “Peter Bergmann and the Invention of Constrained Hamiltonian Dynamics.” arXiv:Physics/0608067v1.
Salisbury, Donald, and Kurt Sundermeyer (2017). “Translation into English of Léon Rosenfeld’s "Zur Quantelung Der Wellenfelder" with Commentary.” European Physical Journal H 42 (1): 23–61.
Schild, Alfred, and Felix A. E. Pirani (1950). “On the Quantization of Einstein’s Gravitational Field Equations.” Physical Review 78: 329.
Schweber, Silvan S. (1994). QED and the Men Who Made It: Dyson, Feynman, Schwinger, and Tomonaga. Princeton: Princeton University Press.
Williamson, Ralph E. (1951). “Fred Hoyle’s Universe.” The Journal of the Royal Astronomical Society of Canada 45: 185–89.
Footnotes
Indeed, Bergmann’s paper contains the cryptic remark that general relativity had “so far not successfully absorbed the existence of quantities possessing half-odd spin.” It is an open historical problem what this statement refers to.
A Lagrangian for General Relativity that contained only first-order derivatives of the metric had first been introduced by Einstein (1916), the so-called
 -Lagrangian, given by Einstein originally only for a specific choice of coordinates. Rosenfeld had actually also considered Lagrangians that change by a total divergence, but only for “internal” symmetries that do not act on the space-time coordinates. It was thus not directly applicable to Lagrangians that changed by a total divergence under general coordinate transformations, but it did apply to Rosenfeld’s tetrad Lagrangian, that changed by a total divergence only under local Lorentz transformations. Rosenfeld’s tetrad Lagrangian was a scalar density under general coordinate transformations. His method can be straightforwardly extended to the case of coordinate transformations, as shown in Salisbury and Sundermeyer (2017).
-Lagrangian, given by Einstein originally only for a specific choice of coordinates. Rosenfeld had actually also considered Lagrangians that change by a total divergence, but only for “internal” symmetries that do not act on the space-time coordinates. It was thus not directly applicable to Lagrangians that changed by a total divergence under general coordinate transformations, but it did apply to Rosenfeld’s tetrad Lagrangian, that changed by a total divergence only under local Lorentz transformations. Rosenfeld’s tetrad Lagrangian was a scalar density under general coordinate transformations. His method can be straightforwardly extended to the case of coordinate transformations, as shown in Salisbury and Sundermeyer (2017).
Concerning these functionals, which were to represent physical quantities, Bergmann and Brunings made the crucial observation in this paper that not all functions of the original field variables and their first derivatives (velocities) possessed a counterpart in phase space. They identified the necessary and sufficient condition for converting a function in configuration-velocity-space into a phase-space function (such functions need to be, in modern parlance, constant along all of the null directions of the singular Legendre matrix) and dubbed quantities that satisfied this requirement “dynamical variables”.
This fact has already been pointed out by one of us (Salisbury 2006). It is hard to say precisely how Bergmann and Brunings came to this erroneous conclusion, since they do not give the details and there is no equation in the paper that is actually wrong. The erroneous statement is that “[t]he proof follows immediately if the functional
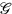 [the linear combination of primary constraints] is substituted in the expression for the Poisson bracket (3.23) [...]” A simple counterexample is to be found in the toy model employed in Pitts (2014), which can easily be parameterized. We would like to thank James Brian Pitts for suggesting this check upon Bergmann and Brunings’s claim.
[the linear combination of primary constraints] is substituted in the expression for the Poisson bracket (3.23) [...]” A simple counterexample is to be found in the toy model employed in Pitts (2014), which can easily be parameterized. We would like to thank James Brian Pitts for suggesting this check upon Bergmann and Brunings’s claim.
That the Hamiltonian of GR would be a constraint even in the unparameterized formulation, the so-called “problem of time,” was only gradually realized in the course of the 1950s.
Joshua Goldberg (2005) has thus labelled Dirac’s approach as algebraic (concerned with the constraints themselves), as opposed to the group theoretical (concerned with the underlying symmetries) approach of Bergmann (and also Rosenfeld).
Interview by DR, 23 June 2011, https://www.aip.org/history-programs/niels-bohr-library/oral-histories/34463 (accessed 21 July 2017).
Dirac had apparently not realized this and Schild brought it to his attention at the time. His wife, Winnie Schild, told one of the authors (DS) of her husband’s pride in having achieved Dirac’s enduring respect through this observation. More importantly, the fact that Dirac had not made the connection underlines that it was not as obvious as Pirani recalled it to be in the interview with DR, making Schild’s previous exposure to Bergmann and Brunings’s work all the more probable.
For more on the mathematical theory (and a brief history) of the generalized inverses of singular matrices, see Rao and Mitra (1971). In the nomenclature adopted there, the Bergmann group was working with a (not uniquely defined) reflexive g-inverse of the Legendre matrix.
A manuscript is in the possession of his widow, Cecile Morette-DeWitt.
17 May 1950, H. P. Robertson Papers, Caltech
Interview by DR and DS, 21 March 2011, https://www.aip.org/history-programs/niels-bohr-library/oral-histories/34461 (accessed 21 July 2017).
Alfred Schild Papers, Dolph Briscoe Center for American History, The University of Texas at Austin.
In the Schild Papers, there is a letter from Pirani dated 22 January 1951, in which the use of the parameter-free formalism is already discussed as a matter of course, seemingly contradicting the above statement. However, in this letter Pirani makes reference to a radio broadcast by Ralph Williamson, which was only broadcast in June 1951 (Williamson 1951), strongly implying a redating of this letter to 1952, making this an instance of the classic mistake of still dating with the old year in January.
The resultant simplifications also allowed Pirani and Schild to identify a mistake in their first paper (see the January 1951/52 letter from Pirani to Schild mentioned in footnote 17): Equation 62 is wrong, no matter where one chooses to close the square bracket: If it is closed at the end of the expression, the sign of the last summand should be changed from plus to minus. If it is closed before the last summand, then that summand needs an additional factor of
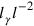 .
.
Alfred Schild Papers
