A central theme of the previous selection of papers was the existence of a variety of divergences, especially the problems generated by the self-energy of elementary particles.1 A common thread that emerges, persisting to this day, is that gravitation might be able to get some kind of foothold in the theory of elementary particles if it could be invoked to provide a physical (non-ad hoc) cutoff at wavelengths that do not conflict with current observations of experimental particle physics data.2 Hence, Einstein’s old question about the role of gravity in elementary particle physics (mentioned in the introduction to part one of this volume) comes alive once again, though not in the way he envisaged it: gravity is rather “put to service” in elementary particle physics as a kind of external resource. However, the notion of a gravitationally induced cutoff took some time to form, and had to wait for a more thorough understanding of the non-linear aspects of the theory, which had remained largely buried under the more tractable linear approximation.3 But this work can be seen as emerging from a well-worn path involving the usage of other cutoffs (minimum lengths) to tame the infinite behaviour of field theories—if gravity suggests a minimum length, then previous work on such ideas can be transferred across from context to context. The papers presented in this part, then, as with many others in this book, were not initially written with quantum gravity in mind; this was a connection only made later once the problem of quantum gravity itself had undergone several changes—not least the idea that quantum gravity involves quantum spacetime.
There were many early suggestions that gravity might act as some kind of divergence “regulator”. The divergences in question were those of QED, and meson theories, which were still, pre-WWII, a somewhat mathematically murky territory (quantum field theory still is, of course). The problem concerned the transitions between quantum states, during which time (a very short time, determined by the uncertainty relations) energy conservation is violated. The great hope for introducing gravitation into elementary particle physics was that it would terminate the wavelengths before they have a chance to reach the problematic high-energy (ultraviolet) wavelengths. Landau (1955) appears to be the first to have suggested this idea based on his more general desire to achieve something beyond quantum field theory, since Landau had a deep distrust of quantum field theory. More specifically, Landau’s field theoretic investigations revealed that even given renormalization, the short-distance behaviour continued to generate infinities (“Landau ghosts”) on account of the approach to the infinite bare masses and couplings (past the “screening” effect that Landau had himself discovered).4 Pauli also makes several comments to this effect,5 including the following remarks in a letter addressed to Abrikosov, Khalatnikov, and Pomeranchuk (in which he assigns priority of the idea to Landau):
I was very interested in Landau’s remarks on the possibility of a connection of the cut-off moment of quantum electrodynamics with gravitational interaction (his article “on quantum theory of fields” in the Bohr-festival volume). It appeals [sic] to me, that the situation regarding divergencies would be fundamentally changed, as soon as the light-cone itself is not any longer a-number equation. Then every given direction in space-time would have some “probability to be on the light-cone”, which would be different from zero for a small but finite domain of directions. I doubt, however, that the conventional quantization of the
-field is consistent under this circumstances. (Zürich, 15 August 1955; in Meyenn (2001, 329))
Given his obvious expertise in both general relativity and quantum field theory, one wonders why he didn’t do more work in the area of quantum gravity. Though as he suggests, it is clear that novel (i.e. unconventional) approaches are probably required (a far cry from his optimistic remarks in the 1929 paper with Heisenberg in which he claims that the general relativistic case would be much the same as electromagnetism). He was, nonetheless, certainly preoccupied with general relativity towards the end of his life—perhaps this “later-life” preoccupation with the unification of quantum and gravity (also shared by Eddington and Schrödinger) contributed in some small way to the poor reputation of the field at this stage.
Developing his earlier remarks to Abrikosov et al. (in the discussion after Klein’s talk), Pauli mentions Landau’s argument that for large cutoff momentum
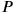, the gravitational coupling between a pair of electrons is of the same magnitude as the Coulomb forces. He notes that Landau’s relation
is the same as Klein’s
(where
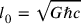). He writes:
[T]he connection [...] of the mathematical limitation of quantum electrodynamics with gravitation, pointed out by LANDAU and KLEIN, seems to me to hint at the indeterminacy in space-time of the light-cone, which is governed by probability laws in a quantized field theory, invariant with respect to the wider group of general relativity. It is possible that this new situation so different from quantized theories, invariant with respect to the LORENTZ group only, may help to overcome the divergence difficulties which are so intimately connected with a-number equation for the light-cone in the latter theories (Pauli’s comments after Klein’s talk, in Mercier and Kervaire 1956, 69).
Pauli’s thoughts were borne out in one way (the light cone structure is affected as he suspects); however, it leaves a challenge behind in dealing with new divergences. As Bryce DeWitt pointed out, in Louis Witten’s important collection, Gravitation: An Introduction to Current Research, from 1962 (less than seven years after Pauli’s remarks),
[I]t must constantly be borne in mind that the “bad” divergences of quantum gravidynamics are of an essentially different kind from those of other field theories. They are direct consequences of the fact that the light cone itself gets shifted by the non-linearities of the theory. But the light-cone shift is precisely what gives the theory its unique interest, and a special effort should be made to separate the divergences which it generates from other diverg’ences. (DeWitt 1962, 374).
In the United States, the first PhD thesis to be written on quantum gravity was that of Bryce DeWitt, under the supervision of Julian Schwinger (at Harvard University, completed in 1949). DeWitt sought to revisit Rosenfeld’s work on the computation of gravitational self-energies (cf. Deser 1957). DeWitt would also revisit this idea of Landau’s that gravity might act as a natural regulator (DeWitt 1964). Though Landau didn’t explicitly mention the Planck scale (he placed the location of the cutoff much higher), Pauli clearly appeared to think that Landau had quantum gravitational effects in mind (or that he ought to have). It is clear that if there is a “fundamental length,” below which ordinary quantum field theoretic processes cannot operate, then one has what Landau sought. DeWitt was able to confirm that (at lowest order of perturbation) when gravity is included, the self-energies of charged particles (and the gravitons themselves) remain finite (though often very large). Here again, as in earlier parts, we see a link between minimum length scales and the notion of limits and domains of applicability of theory and concepts. The question of whether there is a physical cutoff naturally has theoretical links with programmes concerning the existence of a fundamental length, and discrete space(time) in general.6
More indirect, however, was Peter Bergmann’s method of utilising the fact that the gravitational field equations determined particle trajectories free of any notions of divergences. He believed this would follow from the analysis of Einstein, Hoffmann and Infeld, according to which the assumption of geodesy for a free particle’s motion was redundant, since it already could be seen to follow (by a method of successive approximation) from the field equations alone.7
Developing the cutoff idea, and the idea that there might be a minimal (fundamental) length, leads one quite naturally into the idea that space and time might not be continuous, but better modelled instead by a discrete lattice or similar structure. In the early days the cutoff was implemented in the kinematical structure, rather than having it emerge dynamically—whether the cutoff (discreteness) is fundamental or not is a different issue. This was suggested by several people. In a paper from 1930 Ambarzumian and Iwanenko (Chapter 25) argued for the introduction of a spatial lattice structure for physical space as a way of eliminating the infinite divergences from the self-energy of the electron. The basic idea was that the existence of a minimal length would imply a maximal frequency (p.
Another discrete approach, of David van Dantzig (1938; 1956), was motivated by a combination of general covariance (as expressed in Einstein’s “point-coincidence” argument) and the definition of observability in such a theory. He argued that in a generally covariant theory the observable things will be coincidences: events (not shuffled by diffeomorphisms). Van Dantzig argues that in order to not introduce unmeasurable structure into the interpretation or formulation of one’s theory, one should dispense with the existence of a four-dimensional continuum, in favour of a discrete manifold of events. Peter Bergmann describes one such approach as one of “constructing “spaces” that have certain topological properties similar to those of point spaces in the large but do not possess “points” as elementary constituents” (Bergmann, following a talk of Wigner’s: Wigner (1956, 226)). The general approach lives on in several of the current approaches, including causal set theory and dynamical triangulations—though the conceptual basis (especially observability through invariance is absent from the latter case). Bergmann’s comments also draw attention to the “emergence” of continuous spacetime from a discrete structure (a problem at the root of causal set theory, though one in which progress has been made: see, e.g., Major, Rideout, and Surya (2007)).
There was nothing corresponding to paradigms in the early work. Nobody pursued a single programme for long enough—though Bergmann’s initial canonical quantization approach spawned a genuine research programme (along with a family of characteristic questions, having to do with “true observables” and the like) that has persisted. However, in the present day we do have a situation of what seem to be competing, coexisting paradigms (with elements of this sourcebook’s papers as ingredients). We can find the seeds of this landscape in the emergence of various “schools of research”, each tackling the problem of quantum gravity in a unique way. Often these schools themselves had seeds in the distinct tools that the researchers brought from their training, as physicists and mathematicians (recall that before the 1960s, it was rare to find general relativity taught outside of mathematics departments).
The idea at the focus of the papers in this part, that a discretization of space might go some way towards resolving the problems of short-distance physics, is of course rather natural and almost obvious. However, the initial developments were not linked to gravitational physics, although many of the results originally couched in non-gravitational work were carried over into that area. It was eventually realised, for example, that gravitation itself might be able to provide a physical foundation for discrete space and that given the dual nature of the metric field, quantum gravity should lead one to expect a discrete spacetime. Given this, the various results pursued independently of the quantum gravity problem (violation of Lorentz invariance and so on), become directly relevant.
There are three motivations underlying the notion of discrete space(time) in the early work:9
1An ad hoc discretization using a lattice structure—often used as an approximation, for which the continuum limit would be taken later on.
2An operational discretization using fundamental measurement limitations imposed by the uncertainty relations.
3A discretization using a physical cutoff imposed (e.g. by gravity).
The first steps towards a field theory over a discrete space—along the first motivation (in the context of field theory)—were taken by Ambarzumian and Iwanenko in 1930. This paper also includes a discussion of whether time would need to be quantized, along with space, as a corollary. The argument is simple: a minimum length implies a maximum frequency which implies a minimum time interval
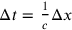.10
They are concerned solely with the infinite self-energies that arise from the point-like nature of electrons. As they note, there seem to be two broad ways out of the predicament: give the electrons a finite size, or else restrict the spatial resolution to which one can probe (placing a limit on the validity of the theory—motivation two above). Since the former was thought to be not possible in quantum mechanics, they opt for the latter strategy. They resolve this “problem of space” by introducing a cubic lattice with grid points separated by some constant factor,
, to be determined (such that ordinary quantum theory is recovered as
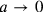). Differential equations are then replaced by discrete, difference equations.
This was followed by Heisenberg,11 Ruark, March and several others, including, in England, Henry Flint. Flint was an interesting case, since he had his eye on the problem of unification of relativity and quantum mechanics in his work on fundamental length (via “ultimate measurements”—again, corresponding to the second motivation).12 The Ambarzumian and Iwanenko paper was also directly cited by Schild, in his paper on discrete spacetime (included in this volume).
There were some other interesting attempts for “quantizing space” in the 30s. The most interesting is perhaps John Von Neumann’s (unpublished) proposal from 1937.13 Von Neumann distinguishes two kinds of singularity: the point-particle singularity and the infinite degree of freedom singularity (resulting from the infinite number of parameters needed to describe a field). In a letter to Rudolf Ortvay from 1938 he describes his model for discrete spacetime as follows:
• (1): The
,
,
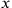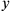coordinates and the
are non-commuting operators.
• (2): The order of magnitude of commutators is
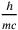. (That is to say, this is the uncertainty associated with a simultaneous measurement of coordinates.)
• (3): The whole structure has the Lorentz-symmetry.
• (4): Each of the
,
,
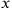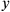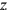coordinates has a discrete spectrum:
,
, ...
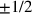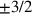• (5): The spectrum of the time
is continuous, from
to
.
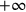• (6): When 4. and 5. are combined with 3. this comes out:
Given four real numbers,
,
,
, the spectrum of the operator
is as follows:
• (a): If
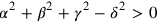then it is discrete:
,
, ... ,
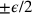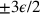where.
• (b): If
(indeed even when
) then it is continuous from
to
.
So this a “discrete” crystalline space with “continuous” time, which has not only spherical symmetry (even though it is a “crystal”!), but is even invariant with respect to changes of the reference system given by Lorentz transformations, and so shows the proper Lorentz-FitzGerald contraction phenomena. (This is made possible, of course, by the non-commuting nature of the coordinates.) (von Neumann, letter to Rudolf Ortvay: March 17, 1938 [Rédei 2005, 22])
In a letter to Dirac (dated January 27, 1934) he writes:
It should be perhaps desirable, to have operators,
,
which gave discrete (point) spectra, in order to avoid the difficulties connected with the point electron (in electrodynamics). (Rédei 2005, 21)
Dirac replied the following month (February 28, 1934) pointing out that the model was not invariant under displacement of the origin of the reference frame defined by the
,
,
.
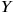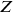Quantization here is viewed, then, as a cutoff to prevent the ability to resolve to point-like distances. The problem with such accounts is that they are physically ad hoc (motivation one from above). Von Neumann did not pursue the idea further for this reason: “because [he] considered it very artificial and arbitrary” (Rédei 2005, 22).
Heisenberg was inspired primarily by the second motivation, though it mixed with the first, in order to tame the infinite self-energy of electrons.14 His first thoughts about discretisation can be found in a long letter to Bohr from March 1930 (translated into English in Carazza and Kragh (1995), along with a reconstruction of the logic of the argument it contains)—one wonders whether he was aware of Ambarzumian’s and Iwanenko’s work, which is remarkably similar (as mentioned, Ambarzumian and Iwanenko note, at the proofs stage of their paper, that they were aware of Heisenberg’s attempt, though it is hard to discern whether their work was initially written without knowledge of this). The idea is also to divide space up into a cubic lattice, where the cells have volume
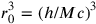. The length
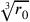(the electron radius) was then the “elementary length”. He called the world described by this theory “gitterwelt” (“lattice world”). The self-energy of an electron would be rendered finite in the gitterwelt—a point Heisenberg returned to in his paper “Die Selbstenergie des Elektrons” (submitted in August of that year). As Heisenberg also notes, in the given scheme differential equations would have to be replaced with difference equations.15 A central problem, as Heisenberg saw it (and as would deter others from the discrete space idea) was that relativistic invariance was spoiled by any scheme that introduced a fundamental length—this assumption was progressively taken apart in papers from the late 1930s onwards. (Heisenberg also pointed to difficulties in making the space isotropic; as well as with energy, momentum, and charge conservation: for these reasons he asked Bohr whether he thought the idea “completely mad”!) But beyond this breakdown of Lorentz invariance, the other target of Heisenberg’s 1930 paper was to show that there are wider problems with field theory that go beyond the problem of infinite self-energy—this became part of a general programme of getting clearer on the distinct kinds of divergences in physical theories (on which, see the introduction to the previous part of this volume).
In his 1938 paper (Chapter 26: “Über die in der Theorie der Elementarteilchen auftretende universelle Länge”), Heisenberg explicitly ignores gravitational interactions “which hardly play a role in nuclear physics,” focusing on
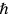and
alone. This is part of a general to and fro with respect to the role of gravitation in elementary particle physics. However, when discussing the “universal length” he does briefly return to the issue, though again to dismiss gravity’s role in the fundamental length. As is standard, he considers the electromagnetic analogy, comparing the gravitational interaction of photons with the electrical interaction of electrons. But he notes a crucial dis-analogy: introducing the gravitational constant (Heisenberg uses
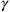rather than
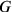) together with
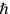and
can be combined to generate the (Planck) length:
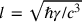(which Heisenberg computes to be
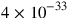cm). However, given the vast distances separating these domains, Heisenberg points out that the problems ass’ociated with his
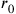(the electron radius) ought to be resolved first, as the most urgent task. In other words, there is a practical argument here for the neglect of issues having to do with quantum gravity.
The reason for this urgency were the difficulties faced by Fermi’s theory of
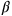decay, based on Pauli’s neutrino hypothesis, which was found to suffer from divergences of an extreme (i.e. unrenormalizable in modern parlance) kind—involving the divergence of (Born approximation) cross sections as the energy of the incident particles went to infinity—so that the perturbation technique for treating interactions didn’t give sensible answers.16 Of course, we know that this problem was pointing to a limit with the then current quantum field theory. But Heisenberg, viewing Fermi’s theory as a fundamental (and unified, in terms of weak and strong forces, with a single coupling constant) theory, took it to point to another source in which one could only resolve distances to certain distances, again close to his
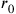.17 In this case Heisenberg drew attention to the particle multiplicity (“explosionen”) in cosmic ray showers in which many particles are created: the particle production would limit the resolution (so that
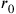represents a fundamental limit in this sense: physics becomes “turbulent” at shorter lengths as the coupling blows up). Of course, there was a limit, but the limit was theoretical rather than practical: there was a layer of particle physics below that captured by Fermi’s theory. The short-distance, strong interaction physics that followed this was a major impetus to quantum gravity physics since gravitational and strong interactions had similar non-linearities (due to the self-interacting nature of the forces)—though, of course, gravity is universal (couples to all sources of energy equally). Hence, a new analogy between these forces, and to a lesser extent with electrodynamics, took hold.18
We have seen that Bronstein had already written on related issues in 1936, pointing out that there exist quantum measurement restrictions beyond the commutation relations in the case of gravitational measurements, since there cannot be bodies of arbitrarily large mass density (cf. Gorelik and Frenkel 1994, 106). Bronstein thought this called for a revision of spacetime concepts (as did Heisenberg, though for different reasons). Unfortunately, his untimely death means that we don’t know how or if he intended to pursue this revision.
The third motivation was discussed, mostly informally, in our pre-1950 period, by Pauli and Landau amongst others, but the idea was not fully developed in published form beyond mere suggestions.
Hartland Snyder’s is probably the best known early work on discrete spacetime—the paper is truly a citation classic, with 1714 citations at the time of writing.19 In this case the resulting spacetime is explicitly presented as quantized, with the spacetime coordinates themselves represented by Hermitian operators with discrete spectra. We have already seen this basic idea, of course, with Heisenberg and von Neumann. The innovation is to properly formalise the idea and establish that the discrete space idea need not violate Lorentz invariance.
Snyder (1947) returned to the subject the following year, with a paper applying the quantized spacetime concept to the electromagnetic field. There is then a trail leading from Snyder to Schild, in which the mathematical properties of quantized spacetime are uncovered.20
C. N. Yang (Chapter 28) tackled a serious issue with Snyder’s model, namely that it violates translation invariance whenever the coordinates are not a continuum. However, a continuum clashes with the fundamental (i.e. non-epistemic) minimum length of the model.21 Yang resolves the translation issue, but a problem of scale persists, namely in the form of a curvature of the universe at odds with what we observe (curvatures are of the order of the Planck scale rather than the Hubble radius).
It is rather interesting that Alfred Schild published his work on discrete spacetime around the same time that he transitioned into research on the canonical quantization of general relativity, following Dirac’s influential 1949 lectures at the International Mathematical Congress in Canada, which Schild attended with his Masters student Felix Pirani.22 Yet there is no mention of gravity in his paper on discrete spacetime, despite the fact that together with Pirani, Schild explicitly quantised the spacetime metric. This clearly reveals (perhaps rather surprisingly) that the project of “quantization of gravity” had not yet been linked to what we now call “quantum spacetime.” The focus is instead on the construction of a discrete model of spacetime that is as close as possible to Lorentz invariant, and the context is the problematic divergences of standard quantum field theory. Schild’s basic object is a hypercubic lattice, with time coordinate included amongst the spatial coordinates. He deals with (
) Lorentz transformations that map a 3-lattice onto itself (where the 3-lattice takes on integer coordinates).
While Snyder’s approach was indeed Lorentz invariant, it made use of the rather awkward idea that spacetime coordinates were non-commuting operators (so that spacetime functions become Hilbert space operators) and was not translation-invariant. Schild uses coordinates that are integer multiples of a fundamental length (rather than having eigenvalues that are integer multiples as with Synder), and so more along the lines of the proposals of Ambarzumian and Iwanenko et al.. Schild’s goal is likewise to show that a common objection against discrete approaches to eliminating the divergences—that they violate Lorentz invariance due to the frame dependence of the “minimum” cell size—is only partially correct since one can construct models that are invariant under a large subgroup (the discrete subgroup) of the Lorentz group. These, he suggests are in fact physically viable (unlike Snyder’s and Yang’s), and cast in a model closer to ordinary spacetime, thus undermining a host of common objections and making discrete models in principle a genuine possibility for fundamental physical theory—though, as he admits, his own model suffers from physical inconsistencies to do with a radically oversized minimal velocity.23
Nathan Rosen (Chapter 29) introduces statistical considerations into the treatment of a discrete space: his elementary volumes are related to position measurement uncertainties (that is, to practical limitations: no infinitesimal measurement rods, therefore no physical point-like measurements). More specifically, the measurement of spatial coordinates of elementary particles (electrons) introduces inaccuracy into the measurement results such that repeated measurements will generate values sitting around the mean of a Gaussian distribution. His aim is, as with other proposals we’ve considered, to eliminate singularities (relating to the second motivation again). The resulting picture is not so very different from the Synderian one of a non-commutative space. However, the discreteness here is epistemological, coming from the difficulties involved in pinning down a spacetime point.
There is a very (later) Eddingtonian quality to this, especially the splitting of the abstract space from the observable space, which corresponds to Eddington’s geometrical and physical frames.24 Volumes in the observable space correspond to points in the abstract space. Lorentz invariance is preserved in this scheme only in the abstract space; yet Rosen suggests that a kind of translation manual could be established between transformations in this space and real physical transformations in the observable space.
There is also an interesting parallel here to some of the issues regarding the “reality of spacetime points” (e.g. in the context of the hole argument in general relativity). Rosen argues that the value of a physical quantity at a point is not directly observable, so that physical laws should not be based on such quantities. What is not clear is whether, according to Rosen, the world (ontology) tracks epistemology so that our laws must be written this way because the world is that way so that only the mean values of quantities over volumes have any physical meaning at all.
Rosen reviewed a closely related paper by Averbah and Medvedev in 1949. He also later returned to a similar idea, writing with Asher Peres, in 1960, though this time explicitly linking to measurement of the gravitational field. By this stage they viewed the existence of quantum uncertainties in these measurements (in the mean values of the Christoffel symbols) as pointing to the necessity of quantizing the gravitational field. Though we don’t see any explicit discussion of the “discrete space-gravitation” connection, the works presented here nonetheless contain crucial evolutionary steps. The recognition that playing around with the structure of space(time) might offer up cures for some of the difficulties of quantum field theory was an early one; linking this up with the way in which general relativity includes the geometrical structure of spacetime as one of the dynamical variables took somewhat longer.
References
Brown, Laurie M. (1993). Renormalization: From Lorentz to Landau (and Beyond). Berlin: Springer.
Brown, Laurie M., and Helmut Rechenberg (1996). The Origin of the Concept of Nuclear Forces. Bristol; Philadelphia: Institute of Physics Publishing.
Carazza, Bruno, and Helge Kragh (1995). “Heisenberg’s Lattice World: The 1930 Theory Sketch.” American Journal of Physics 63 (7): 595–605.
Cushing, James T. (1990). Theory Construction and Selection in Modern Physics: The S Matrix. Cambridge: Cambridge University Press.
Dantzig, David van (1938). “Some Possibilities for the Future Development of the Notions of Space and Time.” Erkenntnis 7: 142–46.
——— (1956). “On the Relation Between Geometry and Physics and the Concept of Space-Time.” In Jubilee of Relativity Theory: Proceedings, edited by André Mercier and Michel Kervaire, 48–53. Basel: Birkhäuser.
Deser, Stanley (1957). “General Relativity and the Divergence Problem in Quantum Field Theory.” Reviews of Modern Physics 29 (3): 417–23.
DeWitt, Bryce (1962). “The Quantization of Geometry.” In Gravitation: An Introduction to Current Research, edited by Louis Witten, 266–381. New York: Wiley.
——— (1964). “Gravity: A Universal Regulator?” Physical Review Letters 13 (3): 114–18.
Gorelik, Gennady E., and Victor Ya. Frenkel (1994). Matvei Petrovich Bronstein and Soviet Theoretical Physics in the Thirties. Basel: Birkhäuser.
Hagar, Amit (2014). Discrete or Continuous? The Quest for Fundamental Length in Modern Physics. Cambridge: Cambridge University Press.
Ivanenko, Dimitri (1931). “Die Beobachtbarkeit in Der Diracschen Theorie.” Zeitschrift Für Physik 72 (9–10): 621–24.
Klein, Oskar (1956). “Generalisations of Einstein’s Theory of Gravitation Considered from the Point of View of Quantum Field Theory.” In Jubilee of Relativity Theory: Proceedings, edited by André Mercier and Michel Kervaire, 58–71. Basel: Birkhäuser.
Kragh, Helge, and Bruno Carazza (1994). “From Time Atoms to Space-Time Quantization: The Idea of Discrete Time, ca 1925–1936.” Studies in History and Philosophy of Science 25 (3): 437–62.
Landau, Lev D. (1955). “On the Quantum Theory of Fields.” In Niels Bohr and the Development of Physics, edited by Wolfgang Pauli. London: Pergamon Press.
Major, Seth, David Rideout, and Sumati Surya (2007). “On Recovering Continuum Topology from a Causal Set.” Journal of Mathematical Physics 48 (032501).
Mercier, André, and Michel Kervaire, eds. (1956). Jubilee of Relativity Theory: Proceedings. Basel: Birkhäuser.
Meyenn, Karl von, ed. (2001). Wolfgang Pauli: Wissenschaftlicher Briefwechsel Mit Bohr, Einstein, Heisenberg U.a. Vols. Vol. 4, Part 3: 1955–1956. Berlin: Springer.
Oppenheimer, J. Robert, and Hartland Snyder (1939). “On Continued Gravitational Contraction.” Physical Review 56: 455–59.
Rédei, Miklós, ed. (2005). John von Neumann: Selected Letters. Providence: American Mathematical Society.
Rickles, Dean (2014). A Brief History of String Theory: From Dual Models to M-Theory. Berlin / Heidelberg: Springer.
Rovelli, Carlo, and Simone Speziale (2003). “Reconcile Planck-Scale Discreteness and the Lorentz-Fitzgerald Contraction.” Physical Review D 67 (064019).
Rueger, Alexander (1992). “Attitudes Towards Infinities: Responses to Anomalies in Quantum Electrodynamics, 1927–1947.” Historical Studies in the Physical and Biological Sciences 22: 309–37.
Snyder, Hartland (1947). “The Electromagnetic Field in Quantized Space-Time.” Physical Review D 72: 68.
Wess, Julius (2001). “Nonabelian Gauge Theories on Noncommutative Spaces.” Communications in Mathematical Physics 219 (1): 247–57.
Wheeler, John A. (1968). “Superspace and the Nature of Quantum Geometrodynamics.” In Battelle Rencontres: 1967 Lectures in Mathematics and Physics, edited by Cécile DeWitt-Morette and John A. Wheeler, 242–307. New York / Amsterdam: W. A. Benjamin.
Wigner, Eugene P. (1956). “Relativistic Invariance of the Quantum Mechanical Equation.” In Jubilee of Relativity Theory: Proceedings, edited by André Mercier and Michel Kervaire, 210–26. Basel: Birkhäuser.
Footnotes
The alternative, to be found in superstring theory, is to postulate a finite size for the elementary entities (in the earlier period, this would have been, e.g., the electron radius).
What the non-linear analysis eventually revealed was that gravity’s divergences were more complex than those of electrodynamics, since they involved a shifting of the light cone so that light cone singularities would be “smoothed out” by fluctuations in a quantum theory of gravity (a nice result of the quantum geometry inherent in quantization of the metric): Klein 1956; Landau 1955; Deser 1957. We return to this briefly below.
Later work would reveal that such Landau ghosts could be dealt with in the context of renormalization group theory, but at the time it appeared as though quantum field theory was suffering from an incurable illness—for more on this, see Brown (1993, 21).
See also Pauli’s letter to Källén (dated 24th April, 1955: pp. 207–208); Peierls’ letter to Pauli (dated 9th May, 1955: pp. 228–229); Pauli’s letter to van Hove (dated 11th May, 1955: 230–231); Heisenberg’s letter to Pauli (dated 11th, May 1955: pp. 234–235).
As DeWitt puts it: “The dimension
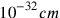constitutes a fundamental limit on the smallness of allowable measurement domains. Below this limit it is impossible to interpret the results of measurement in terms of properties or states characterising individual systems under observation” (DeWitt 1962, 373).
I might also note here that ultimately string theory emerged from the divergences problems facing quantum field theories of fields other than the electromagnetic field (particularly the strong interaction). In particular, since the perturbative approach breaks down when the coupling constant determining the strength of an interaction is large (as in strong interaction physics), alternative approaches were sought in the late 1950s and throughout the 1960s. One of the more popular of these approaches combined Heisenberg’s S-matrix theory with dispersion theory. The S-matrix is a tool to encode all possible collision processes. Heisenberg suggested that one take this to embody what was relevant about the physics of collision processes. In particular, all that was observable were the inputs and outputs of collision processes, observed when the particles are far enough apart in spacetime to be non-interacting, or free. This black box approach to physics was very much inspired by the Copenhagen philosophy. The dispersion relation approach to physics tried to construct physical theories on the basis of a few central physical axioms, such as unitarity (conservation of probabilities), Lorentz invariance, and causality (effects can’t precede causes). These two approaches were combined, by Geoff Chew amongst others, so that the focus was on the analytic properties of the S-matrix. One model for the S-matrix, incorporating some other principles thought to be involved in strong interaction physics, was the Veneziano model. This used the Euler beta function to encode the various desirable properties of the S-matrix. The model was found to be generated by a dynamical theory of strings. (See Cushing (1990) for a detailed historico-philosophical account of the early development of string theory, or Rickles (2014) for a more recent account.)
This same objection to discrete models surfaces again in present-day discussions of discrete space in quantum gravity (a fairly generic prediction of several approaches), especially in the context of loop quantum gravity which directly predicts (at least at the kinematic level) geometrical operators with a discrete spectrum. Given that there is supposed to be a fundamental length (namely the Planck length, and corresponding fundamental times and masses) in these approaches, it makes sense to ask if observers in relative motion will agree on this length: why no Lorentz-FitzGerald contraction for boosted observers, rendering the notion of a minimum length incoherent? Why is a length measurement for the minimum length case not subject to the usual frame dependence? According to Carlo Rovelli (one of the primary architects of loop quantum gravity that itself appears to face the problem) and Simone Speziale, quantum mechanics is the key to avoiding this “discreteness/invariance” conflict: “the minimal length (more precisely, minimal area) does not appear as a fixed property of geometry, but rather as the minimal (nonzero) eigenvalue of a quantum observable [so that the] boosted observer can see the same observable spectrum, with the same minimal area. What changes continuously in the boost transformation is not the value of the minimal length: it is the probability distribution of seeing one or the other of the discrete eigenvalues of the area” (Rovelli and Speziale 2003, 064019). They elaborate as follows, linking directly with issues of quantum spacetime: “The geometry of space comes from a quantum field, the quantum gravitational field. Therefore the observable properties of the geometry, such as, in particular, a length, or an area, are observable properties of a quantum physical system. A measurement of a length is therefore a measurement in the quantum mechanical sense. Generically, quantum theory does not predict an observable value: it predicts a probability distribution of possible observable values. Given a surface moving in spacetime, the two measurements of its area performed by two observers
and
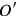boosted with respect to one another are two entirely distinct quantum measurements. Correspondingly, in the theory there are two distinct operators
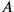and
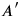, associated to these two measurements. Now, our main point is the technical observation that
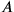and
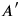do not commute:
![[A,A^\prime ] ̸= 0](../../../media/sources/10/26/EOAineq_26_15.png)
. This is because
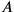and
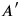depend on the gravitational field on two distinct 2d surfaces in spacetime [...] and a field operator does not commute with itself at different times”. Hagar (2014, §8.4.4) contains a useful, detailed discussion of this problem.
As Rueger makes clear (Rueger 1992, 317), prior to the 1930s there was a sense that the infinities were simply a hangover from the classical theory that if cured first (classically) would not reassert themselves at the quantum level. This was not the case, and it became clear that there existed specifically quantum divergences.
In another paper from the following year, Iwanenko reiterates that the value
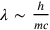also determines a “chronon”: “Dieser Wert hat schon als kleinste definierbare Entfernung zu gelten und nicht der Elektronenradins. Mit der kleinsten Entfernung hängt die kleinste Zeitspanne zusammen” (Ivanenko 1931, 623). As Kragh and Carazza note, there were earlier speculations, with similar results, about time atoms from Pokrowski and Fürth (Kragh and Carazza 1994, 457–458). Indeed, they show that the 20s and 30s were positively teeming with discrete space, time, and spacetime proposals. However, many of them are detached from the central problems of field theories that concern us here.
In fact, in the acknowledgements to their paper, Ambarzumian and Iwanenko refer to analogous work of Heisenberg that they had only just became aware of at the time of publication.
In his notebook (from 1950) there is a section on “The Theory of Relativity and the Quantum Theory” in which he nails down his project: “The underlying theme of this work is the union which exists between the theory of relativity and the quantum theory and the purpose is to portray it by means of geometry and a theory of measurement” (Henry Flint Papers, University of London, Document B53: p. 1).
The manuscript is entitled “Quantum Mechanics of Infinite Systems” see Rédei (2005, 21–22).
Interestingly, Heisenberg had already briefly considered the idea of letting spatial coordinates be non-commuting in 1930 in order to generate a minimum length from uncertainty relations. He put this idea to Rudolf Peierls asking for any suggestions, including any input from Pauli. Julius Wess (2001, 1) claims that Heisenberg relayed it to Peierls (his student), who relayed the idea to Pauli who relayed it to Oppenheimer (his student), who relayed it to Hartland Snyder (his student: see below)! This occurs over a period of 15–16 years.
Carazza and Kragh (1995) argue that Heisenberg did not really endorse a discrete space at this stage, but rather used discreteness only at the level of derivatives with respect to spatial coordinates (which are indeed replaced by discrete, finite differences).
The is the famous four-fermion coupling
which was not properly understood until the electroweak theory was developed, and the machinery of gauge theory was applied, along with Yukawa’s idea of mediation by a new kind of boson (the “U-quantum” or mesotron) which replaced the four-fermion term. The evidence for mesons came in 1937, when they were isolated in cosmic rays. It should perhaps also be said that the realisation that all would not be plain sailing with respect to the other forces of nature shifted the focus onto the peculiarities of gravitation. See Chapters 3 and 4 of Brown and Rechenberg (1996) for a historical study of the Fermi-field theory.
Now the length involves the mesotron mass
,
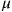, derived from Yukawa’s theory. Note that Heisenberg’s persistent belief in a fundamental, universal length can be seen as more reasonable given that there is a remarkable coincidence between the electron radius and this meson mass (and so the range of the nuclear forces).
As Brown and Rechenberg make clear, the existence of cosmic ray phenomena was pivotal precisely in that it served to delineate the borders of the known physical theories, pointing out exactly when they would break down, see Brown and Rechenberg (1996, 72). Heisenberg was, of course, wrong in thinking that Fermi’s theory was fundamental: there was new physics that Heisenberg was not then privy to.
Of course, this is the same Snyder who had worked with Robert Oppenheimer, in 1939, on the fate of very massive collapsing stars (approximated by an homogeneous, zero pressure ball of dust), showing that a one-way membrane (an “event horizon” in modern parlance) would emerge from the process and that a final singularity would also result—Landau had earlier noted the existence of a critical mass in 1932, and Chandrasekhar had shown in 1931 that the electron degeneracy pressure could not withstand further collapse for stars greater than 1.3 solar masses. It is rather odd that Snyder never made any link between these two streams of his work—continued collapse to a singularity and discrete space—since the former involves the reduction of a system’s dimensions to values small enough (perhaps indefinitely small) to be relevant for the latter. (Oppenheimer and Snyder even write, “Physically such a singularity would mean that the expression used for the energy-momentum tensor does not take account of some essential physical fact which would really smooth the singularity out”, Oppenheimer and Snyder (1939, 456). Later, John Wheeler would bring the two together via the Planck length: two areas where the “dynamics of geometry” fails to lend itself to classical analysis (Wheeler 1968, 253–254). This work would lead, ultimately, to Wheeler’s notion of “spacetime foam.”
Bergmann and Brunings briefly refer to Snyder, if only to distance their quantised metric variables from his: their coordinates, as they say, “commute with each other, but not with the energy-momentum densities”. They continue: “The dynamical character of any particle coordinates follows automatically, but probably does not exhaust the physical significance of the coordinate commutation relations” (see Chapter 33). This highlights the continuity, at least, between Snyder’s (and the other related) work on quantized/discrete spaces and quantum gravity research.
We saw above, in footnote 8, how Rovelli and Speziale manage to sidestep the problem by introducing probabilities for measurement outcomes.
Indeed, Schild’s paper appears in the very same journal as Dirac’s paper, in the issue directly preceding that containing the paper that would inspire Schild’s work on the quantisation of the gravitational field.
This shortcoming was partially eliminated by E. L. Hill in 1955 by restricting the values of spacetime variables to rational numbers—partially, because the resulting space does not quite live up to the “discrete” moniker. As Hill notes in a footnote in this paper, his Master’s student, C. N. Kelber was working on this same problem of Lorentz invariance violation at the same time as Schild. There is some correspondence between Schild and Kelber, where the latter explains that he has a model that involves non-homogeneous Lorentz transformations so that the origin is not fixed for all observers (Kelber, letter to Schild, June 21st 1948).
Rosen adds a statement to this effect, though pointing out that he was unaware of Eddington’s work at the time of writing. Interestingly, this information was relayed to Rosen by M. F. M. Osborne, more famous now perhaps as an early econophysicist, but who also did early work on measurement restrictions, and minimal length, in quantum general relativity.