These earliest papers (taken from 1916–1921) suffer from the fact that quantum theory was still in an embryonic state. Quantum mechanics and quantum field theory would have to wait several years before they were even properly formulated, and so could be compared with general relativity (as subsequent parts of this volume will cover). Still, already in these early papers, questions were being posed concerning the proper way to understand the relationship between quantum theory and general relativity. In addition to areas in which there might be modifications brought about by one theory to the other (conflict), or overlaps of some kind (coexistence), there were also “borders” raised between the theories that persisted throughout future changes in physics in the period before 1950. Hence, although one cannot reasonably call this research “quantum gravity,” many elements of this pre-history nonetheless directly inspire that later research and, more importantly, serve to demarcate the domains of the ingredient theories.
What is crucial to note in this period is that the developments in quantum theory and in general relativity are often made by the same people, laying the foundations of both simultaneously. For example, as the field equations of general relativity were entering their ultimate form (“the final stage in which the battle over the field equations is being fought out”1), Einstein was corresponding with Arnold Sommerfeld about the potential impact of his new theory on contemporary issues in quantum theory. Sommerfeld appears to have thought that general relativity might be of relevance (imposing new constraints and so on) with regard to spectral physics and the Stark effect (Sommerfeld 2000, 438). Einstein writes back:
General relativity is unlikely to be able to assist you, because it practically coincides with the more restricted theory of relativity for those problems. [...] [A]ny other theory that corresponds with relativity in the restricted sense can be taken over in the general theory of relativity through simple transformation, without the latter delivering any new criteria. Thus you see that I cannot help you in the least. [Einstein, letter to Sommerfeld, [Berlin] 9 December 1915 (Schulmann et al. 1998, 159)]
However, in his paper “Näherungsweise Integration der Feldgleichungen der Gravitation” (1916, Chapter 2 in this volume), Einstein claims that his newly constructed theory of gravitation would itself need to be modified by quantum theory along the same lines as classical electrodynamics so as to keep gravitationally radiating systems stable. Hence, without a quantized emission of gravitational energy, the system would (eventually) continuously radiate away all its energy and collapse. It is, perhaps, no surprise that Einstein was working in tandem on the quantum theory of emission and absorption of radiation at the same time he wrote this paper on gravitational radiation, and the same terminology and concepts can be found in both contexts.
The Einstein paper features further, and deeper, analogies between electromagnetism and general relativity, and these analogies continued to play a role in later research on quantum (and classical) gravity.2 For example, just as an accelerated electrically charged particle will emit electromagnetic waves (at the velocity of light), gravitational waves were a direct prediction of the linear theory and were also transverse and propagated at the speed of light. The linear approach (a first approximation to the full non-linear theory, again analogous to electrodynamics’ standard perturbative approximation where the coupling constant is taken to be small) involves decomposing the metric
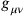apart as follows:
|
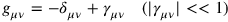
1.1 |
The small perturbations (representing deviations in the spacetime metric away from flat space3)
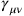are defined against a flat, Minkowski spacetime background (a “Galilean space” in which
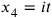). The calculation follows exactly the same route as for the retarded electromagnetic potentials, giving the various analogous properties mentioned above, including the existence of gravitational waves.
This perturbative approach (employing a background metric against which the properties of the perturbations are defined) forms one of the standard methods in later work. As we see in Part III, Rosenfeld uses just such a framework in his early quantization and it informs the work of Fierz and Pauli in unpacking the properties of gravitational quanta (massless particles with two helicity states)—Jacques Solomon raised an early warning about the problems faced when ignoring the full non-linear theory; Dmitri Ivanenko noted that during a discussion at the Turin Congress (in 1956), Pauli expressed skepticism about the generalisation of results from the weak field approximation to the full theory in the case of gravitation (Ivanenko 1956, 355).
Einstein published a second paper on gravitational waves in 1918, correcting some problems in the 1916 paper and drawing attention to some crucial differences between the electromagnetic and gravitational cases (which had led Einstein to a serious error of calculation).4 The most important of these concerned the differences in moments of the radiation: dipole in the case of electrodynamics (as he had also assumed held for gravity in the 1916 paper), but quadrupole in the case of gravitation: “[A] mechanical system which permanently retains spherical symmetry cannot radiate” (Einstein 1918, 23). Einstein reiterates the point regarding the likely modifications of general relativity brought about by a completed quantum theory, since the results still indicated energy loss due to thermal agitation (Einstein 1918, 23).
Just one year later Einstein can be found speculating about the role of gravitational fields in the constitution of elementary particles of matter (electrons) in his paper “Do Gravitational Fields Play an Important Role in the Constitution of the Elementary Particles?”.5 The idea is to get discrete particles (electrons) out of a continuous field theory. John Wheeler would later resurrect something similar in the early 1950s with his “Geon project” (where a geon is a “gravitational electromagnetic entity”), in which the elementary particles are reduced to geometrical and topological aspects of such entities (see, e.g. Wheeler (1955)).6 Once this shift in Einstein’s thinking had occurred, he didn’t waver again and sought only classical theories as opposed to quantum gravity theories. However, there were additional important developments in Einstein’s work. Not least among these was the result, obtained with Infeld and Hoffmann (Einstein, Infeld, and Hoffmann 1938), that enabled particle trajectories (equations of motion) to be derived from the field equations—this would have a direct impact on Peter Bergmann’s earliest work on quantum gravity (Bergmann 1949). Bergmann was concerned with using this feature of generally covariant theories to eliminate the divergences caused by particle interactions (infinite interaction terms) in field theories: field singularities (particles) can be determined from the field equations. In this project, it is clear that Bergmann has Einstein’s old question, of the constitution of elementary particles, in mind.
The general idea that quantum and gravity would have to meet in some way in a complete formulation of the world seems to have been accepted by other physicists of the time, and motivated subsequent early work and commentaries on the subject. While there were many remarks pointing to the clash, there wasn’t much real detailed work to resolve the problem, or even any systematic investigation, until Léon Rosenfeld’s efforts in 1930 (following on from initial work on quantum electrodynamics), discussed in the next parts. As mentioned above, until quantum theory was established on a firmer footing, it would have been impossible to tackle the problems of unification.
While the majority of the Eddington paper (Chapter 3), from 1918, amounts to a popular presentation of general relativity7, it also contains the first statement that we know of concerning the relevance of the Planck length in connection with (quantum) gravitational physics, and includes a statement of its importance in any future theories that wish to merge gravitation (
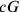) and quantum theory (
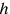).8 Eddington sees that the minute nature of the fundamental length generated from the theoretical constants meant that the structure of a unifying theory will be hidden until we can probe down to the “quadrillionth or quintillionth of a centimetre”.9 Though the numerical value he cites is not as we write it today (perhaps a computational error?), given that he speaks of the fundamental unit length one achieves by combining the three basic universal constants
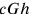, and there is only one way to do this, we must assume that he has in mind the Planck length nonetheless.
Hence, by 1918 we already have two arguments (however coarsely and briefly expressed) for the necessity of a unification of quantum theory and general relativity (or gravitation and quantum phenomena), both for consistency and for reasons of theoretical unity. It is not yet quantum gravity in the sense of quantization that is being proposed. Indeed, nothing is being proposed at this stage; rather, it is left as a future project. Both Einstein and Eddington would soon diverge rather radically from the three motivations outlined earlier. Though Eddington stuck to the project of unification of quantum theory and general relativity, until his death, his approach departed from the reductionist (deeper probing) method he suggests in Paper 2. Perhaps forced by the sheer distance of scales (from known physics) we see in the Planck units, Eddington began to employ a non-experimental methodology, culminating in his (posthumously published) Fundamental Theory (Cambridge University Press, 1946).
George Barker Jeffery (9 May 1891—27 April 1957) was one of the few physicists to directly acknowledge Einstein’s remarks about the probable modifications that quantum theory would bring about in the theory of gravitational radiation.10 The main result of the paper (Chapter 4) is not entirely novel, though he appears to have discovered them independently: Jeffery himself notes that he had been unaware until publication that Nordström had only just derived similar results to his. The central outcome is an extension of Schwarzschild’s line element (of space surrounding a point) to the combined electromagnetic and gravitational case (considering particles with charge and inertial mass), done by modifying the
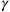-term as:
|
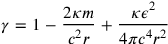
1.2 |
In this case the point is a singularity of both fields (i.e. there are two singularities), rather than the gravitation field alone:
|
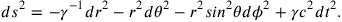
1.3 |
Oliver Lodge discusses Jeffery’s proposal as an attempt to “ascertain something about the state of the aether close to an electron” (Lodge 1921, 392), which indicates something about the transitionary state of physics at the time. But he also rightly points out that the paper involves thinking about the status of fields near to points, and the question of whether the elementary particles really have structure, which itself leads to the additional question of radiation’s interaction with elementary particles in such cases (especially as regards absorption of radiation by elementary particles). As he puts it: “a study of what happens to radiation when it impinges on, or penetrates between the ultimate elements of matter—in fact, a study of the whole behaviour of a stream of radiation at its two ends, the source and the sink—is obviously of great importance” (Lodge 1921, 392). Such reasoning is hardly shot down by the act of bringing those “ultimate elements of matter” in line with quantum principles.
The ultimate aim of Jeffery’s paper was to show how the gravitational field might be involved in the structure of the electron (in line with Einstein’s “turning point” mentioned above), with the conclusion that the electrical and mass potentials would offer some kind of stabilizing effect by opposing each other.11 This brings him to Einstein’s rather pessimistic remarks about the fate of general relativity at the hands of quantum theory from the 1916 paper (Chapter 2), regarding the instability of the atom in the face of continuous classical gravitational radiation. Jeffery believed that the problem could be evaded. Einstein was not convinced by Jeffery’s idea:
I unfortunately cannot share your optimism regarding the solution to the quantum problem. I believe that the theory of relativity does not bring us a step closer, at least in its current form. I am convinced that the two-body problem will not lead to a discrete manifold of paths but to a continuous one. (Einstein, letter to Jeffery [Berlin], 18 March 1921 (Kormos-Buchwald et al. 2009, 85))
But, as we have seen, Einstein had already started down a path that followed the spirit if not the letter of Jeffery’s approach (namely, using GR, or some modification of it, to recover quantum behaviour). In other words, Einstein’s earlier assumption about quantum restrictions of gravitation were replaced by the view that quantum phenomena are to be derived from general relativity and thus are not fundamental. However, here Einstein does not indicate this aspect of his thinking to Jeffery, and indeed the quote above looks largely negative as far as the entire project of getting quantum from relativity goes.
Though Einstein was followed by several others along the “unified field theory” path, the majority view was that his earlier pessimism should and could be responded to without rejecting quantum theory, as we see in the papers that follow. In the next part, the two ingredient theories are worked out in more detail along exactly the lines of figuring out how generally relativistic principles and quantum principles can co-exist, at least in a formal-structural sense.
References
Bergmann, Peter G. (1949). “Non-Linear Field Theories.” Physical Review 75 (4): 680–85.
Eddington, Arthur S. (1922). “The Propagation of Gravitation Waves.” Proceedings of the Royal Society of London A 102 (716): 268–82.
Einstein, Albert (1918). “Über Gravitationswellen.” Sitzungsberichte Der Königlich Preußischen Akademie Der Wissenschaften Berlin, 154–67.
Einstein, Albert, Leopold Infeld, and Banesh Hoffmann (1938). “The Gravitational Equations and the Problem of Motion.” Annals of Mathematics 39 (1): 65–100.
Gorelik, Gennady E. (1992). “First Steps of Quantum Gravity and the Planck Values.” In Studies in the History of General Relativity, edited by Jean Eisenstaedt and A. J. Kox. Boston: Birkhäuser.
Ivanenko, Dmitri (1956). “Non-Linear Generalisations of the Field Theory and the Constant of Minimal Length.” Supplemento Al Nuovo Cimento 6: 349–55.
Kennefick, Daniel (1998). “History of the Radiation Reaction Problem.” In The Expanding Worlds of General Relativity, edited by Hubert Goenner, Jürgen Renn, Jim Ritter, and Tilman Sauer. Boston: Birkhäuser.
Kormos-Buchwald, Diana L., Ze’ev Rosenkranz, Tilman Sauer, József Illy, and Virginia I. Holmes (2009). The Collected Papers of Albert Einstein, Vol. 12. Princeton: Princeton University Press.
Lodge, Oliver (1921). “The Gravitational Field of an Electron.” Nature 2691 (107): 392.
Schulmann, Robert, A.J. Kox, Michel Janssen, and József Illy (1998). The Collected Papers of Albert Einstein, Volume 8. Princeton: Princeton University Press.
Sommerfeld, Arnold (2000). Wissenschaftlicher Briefwechsel. Band 1: 1892–1918. München: GNT-Verlag.
Vizgin, Vladimir P. (2011). Unified Field Theories: In the First Third of the 20th Century (Translated by Julian Barbour). Boston: Birkhäuser.
Wheeler, John A. (1955). “Geons.” Physical Review 97 (2): 511–36.
Footnotes
As described in a letter to Sommerfeld, [Berlin] 9 December 1915 (Schulmann et al. 1998, 159).
Gennady Gorelik (1992) briefly discusses the role of the electrodynamical-gravitational analogy in this phase of Einstein’s thinking. He argues, rightly we think, that an overly strong analogy persisted in the decades following, fooling physicists into thinking that the task of constructing a quantum theory of gravity was going to be along the same lines as the quantum treatment of electrodynamics. Much of this was an artefact of the linearised approximation scheme Einstein used in 1916, which eradicates the distinguishing (and very difficult) features of gravitation. Given the tractability of the linear approximation, this was the scheme that was used in most of the early direct quantization attempts.
A “deviation of the continuum from one that is field-free” in Einstein’s own words (Gorelik 1992).
The prediction of waves would form one of the central motivations for quantum gravity in the 50s. Readers will no doubt be aware of Einstein’s double about-face in 1936, leaving him back where he started! Einstein was briefly fooled into thinking that the existence of gravitational waves was an artefact of the linear theory (true only for weak fields), so that when the non-linear field equations were used instead, the waves were no longer physical or energy-transporting. Together with Nathan Rosen, he had originally argued that (cylindrical) gravitational waves are unreal, in a paper entitled “Are Gravitational Waves Real?” (submitted to Physical Review). But following Howard Robertson’s referee report pointing out a serious flaw in their paper (initially dismissed as erroneous by Einstein), he switched his position (though publishing in a different venue, the Journal of the Franklin Institute, and without acknowledgement of Robertson’s helpful critique). For a discussion of this episode, see Kennefick (1998)—the title of Kennefick’s book (Travelling at the Speed of Thought) refers to Eddington’s characterisation of gravitational waves in 1922 (Eddington 1922, 269).Of course, as a practical prediction the result suffered from the fact that there were no known sources (terrestrial or astrophysical) that could generate energies of sufficient magnitude to be detected—this changed in the 1960s.
According to Vizgin (2011, 163), this marks the birth of Einstein’s switch to “unified field theory,” in which gravitational (and electromagnetic) fields are fundamental, and discrete atomic particles emergent features. The basic question of whether and to what extent the gravitational field might be involved in the structure of the electron also plays a part in Paper 3, by Jeffery (see below).
In order to recover such things as charge and spin, the geon project became rather complex, with e.g. wormholes (multiply connected space) being used to recover charge phenomenology. For more on the history, see Dieter Brill (John Wheeler’s student): http://mediathek.mpiwg-berlin.mpg.de/mediathekPublic/versionEins/Conferences-Workshops/Quantum-Gravity/Thursday/J-A-Wheeler-Geons.html. The geon was originally called “kugelblitz” (ball lightning) by Wheeler. It is interesting to speculate on the origins of the concept in his work on plasma physics for Project Matterhorn: one of his geon models was a toroidal geon of the kind that is often invoked in ball lightning research (where it is modeled as a stable, spinning plasma toroid).
This underplays other important aspects of the paper. For example, it includes a particular perspective on the physical content of the general theory of relativity involving the idea that it is a theory of space considered as “the scaffolding constructed from our measures”—a view that retains a degree of modernity.
Hence, here we disagree with Gorelik who assigns priority to Matvey Bronstein in 1936 (see Gorelik (1992, 367)). However, it is true that the first detailed analysis of the extent to which the Planck values encode information about the quantum limits of general relativity (in the sense of measurability analysis) was due to Bronstein. Note that the issue of domains of applicability of theories would return again, firstly in the context of the debate about measurability limitations (alluded to already), and also in the context of a minimum length implied by quantum theory which are also linked to the former in some cases.
Recall that in England a quintillionth is
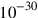. For two more decades, the smallest length relevant to physics was set to
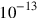in line with the scales set by the existence of known particles (rather than any future combination of relativity and the quantum).
Like Eddington, Jeffery was a Quaker, and had spent time in prison in 1916 as a conscientious objector—Einstein was aware of this writing wittily in his letter to Jeffery that it “is a highly welcome fact that a considerable portion of England’s learned world upholds the pacifist ideal” (Kormos-Buchwald et al. 2009, 85).
This, he thought, might be the result of an analysis of the two body problem in his scheme: a subject for future work. Of course, this problem (exact solutions for the gravitational two-body problem for two point singularities) would ultimately have to wait for new methods in the initial value problem and numerical techniques—though the Einstein, Hoffmann, Infeld paper (1938) is precisely along these lines, and, as we have seen, Bergmann used this method precisely for its ability to avoid interaction divergences. Curiously, Jeffery argues that without including electric charge, the point singularity blows up so that one has “not a solution with a single point singularity, but a solution with a point singularity surrounded by a spherical surface of singularity” (see p.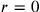 
. Even more curiously, Jeffery speculates that given the light deflection features of general relativity “it would seem to be not impossible that a ray which passed sufficiently close to an attracting particle might be so strongly deflected that it would be permanently entrapped by the particle” (see p.