The Nova scientia is constituted of an incipit, a dedicatory letter and three books. In the incipit,1 Tartaglia promises five books. The first two books pertain to ballistics in the strict sense of the word, while the third is dedicated to a method for measuring distances by sight, a necessary practice for the bombardier, given that the angle of elevation of the cannon was decided based on the distance between the cannon itself and the target. The fourth book was to present firing tables for the bombardiers, more specifically, tables that would show how the range increases or decreases depending on each angle of elevation. These would also permit calculations, according to Tartaglia, on the basis of the data obtained from a single shot. In practice, bombardiers would have been able to use the tables, for example, when the target was not visible but the distance between the target and the piece of artillery was known. The fifth book, finally, was to discuss in detail the characteristics of different flammable materials and the different ways in which they were manufactured as well as opportunities for their use. As Gerhard Arend has pointed out, Tartaglia did in fact discuss some of these themes in another of his works, Quesiti et inventioni diverse.2
2.1 The Dedicatory Letter
The dedicatory letter contains a brief description of the main theoretical findings obtained, the method used to obtain them (also referring to the two missing books), and the social context in which these studies were pursued. Furthermore, in the letter Tartaglia states the physical conception of motion that forms the basis of his theoretical treatment, which, as will be seen, is fundamentally Aristotelian. Finally, the dedicatory letter describes a mathematical instrument fundamental to the art of the bombardier and, above all, fundamental to the modern historian in order to understand the process that led to the birth of modern ballistics. This instrument is the quadrant or square, which permitted the determination of the angle of elevation of the artillery gun (Fig. 2.1):
[…] a square of whichever metal or hardwood is needed. The square must contain a quadrant with its plumb line [positioned] as it appears below in the drawing. Then, one inserts part of the longer side of the square (that is the part BE) into the bore or mouth of the piece, laying it flat along the bottom of the empty barrel, and one lifts up the front of the mentioned piece until the plumb line HD divides the curved side EGF (of the quadrant) into two equal parts (that is at the point G). At this point, one can say that the mentioned piece is straightly elevated at 45 degrees above the horizon.3

Fig. 2.1: Representation of a cannon positioned at a 45-degree angle of elevation as verified by means of the bombardier’s quadrant. From Tartaglia 1558, epistle, second folio (unnumbered), verso.
Tartaglia did not invent the quadrant. This mathematical instrument belongs to a category of measuring instruments whose origins lie in a more remote time in history. As Tartaglia himself states, it was an instrument already long in use, for example, in astronomy, where it was used to measure the elevation of stars above the line of horizon. Integrated into more complex instruments such as the astrolabe, the technique of measurement applied using the quadrant as described by Tartaglia was indeed nothing new. The use of the quadrant by bombardiers, however, obviously originated in more recent times. The diffusion of heavy artillery using gunpowder took hold in the fifteenth century, and with it, the use of the quadrant. It is generally accepted that the quadrant was first used for military purposes during the Hussite Wars, between 1419 and 1434 (or 1439), and that it came into common military use during the Burgundian Wars, between 1474 and 1477.4 The first description of the quadrant as used by the bombardiers goes back to the mid-fifteenth century and is found in the Ex ludis rerum mathematicarum by Leon Battista Alberti.5 However, further research has revealed that the quadrant was already in use in 1410, albeit in a different form and applied to the artillery in a different way, as shown in the image below (Fig. 2.2).6
The technological application of the science of ballistics—which emerged around the mid-sixteenth century—was therefore based on the use of an instrument that had already been in use for at least 120 years. The significance of this fundamental aspect will be discussed later in Section 6.
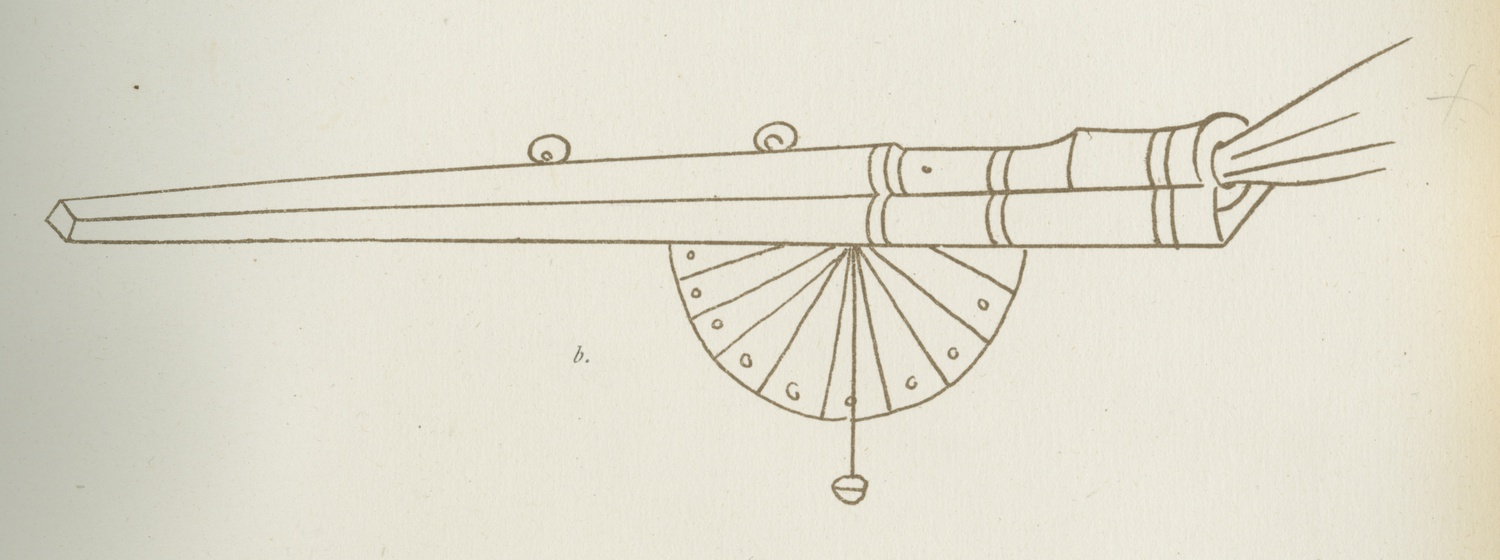
Fig. 2.2: Drawing of a predecessor of a quadrant for bombardiers of 1410. From Essenwein and von 1873, table A. XIX.
2.2 The First Book
The first book covers in depth the physical context in which Tartaglia’s science is set. In his day, Tartaglia had no option other than to move within the conceptual framework of Aristotelian physics. This was based on the premise that the world is clearly divided into two regions with two distinct and separated physical systems: the sub-lunar world and the super-lunar world. Considering that the Earth is taken to be the center of the world, the region in which there is human activity is clearly the sub-lunar world. Aristotle, and therefore Tartaglia, make the distinction between just two types of motion in the sub-lunar region: violent and natural. Furthermore, the objects of the sub-lunar world—subject to movement, either natural or violent—are understood to consist of four elements: earth, water, air and fire. According to Aristotle, the elements earth and water are characterized by their heaviness, while air and fire are characterized by their lightness. In this context, each element tends to reach what Aristotle referred to as its “natural place.” This implies that earth and water—or the objects which contain such elements in high quantity—tend naturally to move downwards, whereas air and fire tend to move upwards. A very straightforward example of natural motion is to imagine an object which has an abundance of the element earth, such as a stone. If the stone is set to move freely from a high place and from a state of rest, it will move downwards as long as there are no obstacles to impede the motion. There is a fundamental difference, however, between violent motion and natural motion, in that violent motion can take place only if there is a specific moving power (possanza movente in Tartaglia’s terminology) that is able to cause a motion, but which at the same time does not move along the trajectory of the motion that it has caused. Natural motion follows a rectilinear path upwards or downwards (if no possible obstacles are considered), whereas all other motions can only occur as violent motions. It is immediately apparent that there is no specific treatment of curvilinear motions in the sub-lunar world, and that rectilinear motions downwards and upwards can be both natural and violent.7
Tartaglia defines natural motion and violent motion in the sixth and seventh definitions of the first book:
Sixth definition.
The natural movement of equally heavy bodies is the movement they accomplish from a higher place to a lower one, perpendicularly and without any violence.
Seventh definition.
The violent movement of equally heavy bodies is the movement they accomplish with effort either upwards or downwards, to the right or the left, and is caused by a moving power.8
Tartaglia’s Nova scientia is based entirely on the concept of the “equally heavy body” (corpo ugualmente grave).9 This is an original concept which Tartaglia describes in detail in the first definition of the first book:
First definition.
An equally heavy body is said to be a body which, according to the heaviness and shape of the matter, is not perceptibly influenced by air opposition during its motion.10
Although it is the first attempt to create a mathematical science of ballistics, the level of abstraction proposed by Tartaglia is remarkable, since he already explicitly asserts in the text that the treatment does not take into consideration the friction caused by the passage of projectiles through the air. Tartaglia is indeed aware that the construction of an axiomatic and mathematical theory of the motion of projectiles could be formulated only if certain factors, such as the resistance of air, were factored out, despite their fundamental nature. Although the Aristotelian doctrine of motion in the plenum provides a qualitative description of the relationship between the motion of a projectile and the density of the matter through which the motion occurs, the formal methods at his disposal, i.e. Euclidean geometry, precluded any quantitative treatment of this aspect. In order to avoid having to account for the effect of the resistance of air, Tartaglia therefore does not proceed with mathematical abstractions, but simply searches for a way that would allow him to ignore this parameter. Consequently, Tartaglia continues to postulate by drawing on purely physical observations:
Nevertheless, an equally heavy body is univocally understood in this work as the body that, in reference to the heaviness and shape of its matter, is not perceptibly influenced in each of its motions by the opposition of the air. Concerning the matter, [it can be] of iron, of lead, of stone or of another material similar in reference to its heaviness. Concerning the shape, this is characterized by such a quality that makes it appropriate to not be influenced (because of its shape) by the opposition of the air during all of its motions. Therefore, among the figures and shapes of the bodies, the wedge-shaped object, that is the pyramidal shape, is the most appropriate among all possible shapes in order [for it] not to be influenced by the mentioned air, provided that by means of a contrivance the body would remain in a position so that its top would always proceed while remaining in front against the impetus of the mentioned air. If the object does not retain such a position, as has been said, it would not work properly as it would not be equally heavy. Without further investigation, we define the spherical figure or shape as the most appropriate among all possible shapes in order to avoid the mentioned opposition of the air in the frame of each kind of motion. This [spherical] shape is most appropriate for the motion on all of its sides and it is equally heavy on all of its sides as well.11
At the roots of Tartaglia’s argument is a more articulated reading of Aristotle’s work, as offered by the works of the Arabic commentators Averroes and Avicenna, which may have continued to serve as vehicles of the Aristotelian doctrines for scholars as late as the sixteenth century.12 In particular, Tartaglia accepts the teaching, which he attributes to Averroes, that considers air to be a heavy body and therefore characterized by a natural downward motion, like water and earth.13 Among his presuppositions, moreover, is the characterization of the bodies constituted of a mixture of elements in terms of heaviness and lightness, which he attributes to Avicenna. According to Avicenna, and as reported by Tartaglia, every body, if it consists of the four elements and is located in air, is bound to fall downwards.14 The framework of Tartaglia, as based on the theories of elements of Averroes and Avicenna, is therefore constituted of projectiles that fly along a heavy medium and that, independently from the matter of which they are composed, they always naturally tend to fall downward. On the basis of such presuppositions, the heaviness of a body, according to Tartaglia, is determined by two parameters: the matter of which it is composed and its shape. Two equally heavy bodies are therefore composed of the same matter, while the specification of the form requires more elaborate investigation. Indeed, depending on the shape of the body, the latter can react differently to the medium, i.e. the air, through which it is thrown. Furthermore, during motion, the body could change its flight behavior with respect to the direction of the motion itself. For this reason, it is not possible to provide a general definition of equally heavy bodies in any mathematical or abstract terms without considering their shape. Tartaglia therefore moves on to a physical and observational examination of all possible shapes, from which he concludes that the only shape that is not affected or, better, that is equally affected by the resistance of the air during motion is, in physical reality, the sphere.15 Tartaglia does not have the formal instruments to determine which shape the moving body must have in order to minimize the effect of the medium. Therefore, he empirically determines which shape allows him to state that the medium always acts in the same manner, independent of the flight position of the object and the density of the medium. To conclude, two equally heavy bodies are made up of the same matter, have the same dimensions, and a spherical shape. Tartaglia remains within the context of the Aristotelian plenum, but looks for the physical conditions that allow him to ignore some of its effects in his theoretical argument.
The first book proceeds by defining all the concepts which are necessary in the second book in order to describe the trajectory of projectiles precisely: time of motion, instant of time, initial and final instant of a motion, interval of time, velocity of motion (equal velocity is when two projectiles traverse the same space in equal intervals of time),16 resistance by the “offended body” (corpo offeso), which is the effect made by the projectile on the body that has been hit, and moving force, described by Tartaglia as the “moving power” of an artificial machine (the cannon) able to launch an object through the air.17
The “Suppositions” (“Suppositioni”) follow the definitions and show how the basic concepts just outlined are correlated. For example, Tartaglia shows how, based on observing the effect of the projectile on its target, it is possible to make deductions about the velocity of the projectile, and that the effects on targets of varying degrees of resistance are different even when the velocity of the projectile is the same. The five suppositions are followed by four axioms (“Comuni sententie”), whose function is to show once again how the concepts provided by the definitions are correlated, with the difference that in this case the correlation is based on observations considered to be evident and unequivocal. The first three axioms deal with natural motion and relate the effect of a falling body on a resistant body (resistente), depending on the height from which the body falls and the resistant body itself. The fourth and last axiom deals with violent motion:
Fourth [common sentence].
If an equally heavy body finds a resistant along its violent motion, the closer the resistant is to the beginning of the motion, the greater the effect is that the mentioned body produces on it.18
As known and as already supposed in the sixteenth century, projectiles continue their acceleration at least until the end of the barrel of the gun, reaching the maximum quantity of motion after a certain interval of time. Nevertheless, Tartaglia, having only Aristotelian dynamics at his disposal, was forced to assume that the moment of greatest velocity, which was for him the greatest “effect,” happened at the beginning of the violent motion, i.e. at the point where the moving force is applied and the mobile begins to move away. The propositions thus highlight the phenomena of the speeding up and slowing down of motion, each distinct from the other in terms of concept. The first two propositions tackle the subject within the realm of natural motion, affirming that, as the distance traveled by a falling object increases, so does the velocity of the motion of this same object, thereby implying that the least velocity will be observed at the moment of the start of the motion. The velocity therefore changes at each moment in time to the extent that there will never be two different instants at which the motion will have the same velocity (Fig. 2.3).

Fig. 2.3: Experiment proposed by Tartaglia to demonstrate the relationship between velocity and the space covered within the framework of natural motion. From Tartaglia 1558, first book, 5r.
The third and fourth propositions tackle instead the phenomena of speeding up and slowing down within the realm of violent motion. In this context, the projectile moves with greatest velocity at the start of the motion, gradually slowing down so that it is possible to deduce that the greater the distance covered, the greater the velocity at departure. Furthermore, every violent motion is said to conclude with the same velocity, regardless of the moving force. This means that what varies is the distance covered and the time taken. The fifth proposition draws a correlation between the speeding up of natural motion and the slowing down of violent motion, albeit a negative one:
Fifth Proposition.
No equally heavy body can travel for an interval of time or a space with a motion mixed of violent and natural motion.19
At this point it is possible to begin reconstructing Tartaglia’s notion of the trajectory of projectiles. Following Tartaglia’s own instructions, one concludes that when a projectile is launched by force, it follows a straight line and slows down until a certain instant when the violent motion stops. At this same instant, the speeding up associated with the natural motion begins. According to this description, the trajectory should correspond to a triangle constructed on the line of the horizon; the greater the elevation of, for example, an artillery gun, the more acute the highest angle in relation to that horizon. A trajectory conceived in this way is the same as the one that can be deduced within the frame of Aristotelian dynamics. However, as can be seen in the diagram, the trajectory as conceived by Tartaglia predicts a curvilinear section (Fig. 2.4).

Fig. 2.4: Representation of the trajectory of a projectile according to Tartaglia. The trajectory is composed of a rectilinear segment, an arc of circumference and a final rectilinear segment turning towards the center of the Earth. The first rectilinear segment and the section of the circumference represent the section of the trajectory’s violent motion. The final rectilinear segment is that of natural motion. From Tartaglia 1558, first book, 7v.
Indeed, Tartaglia could not and did not want to fully reject what could easily be observed by anyone in the sixteenth century at the peak of the revolution of the art of war. In fact, Tartaglia, like any bombardier, was perfectly aware that the trajectory of a cannon ball in reality follows a continuous curve. Nonetheless, he considered the initial part of the trajectory to be a straight line in order to better exploit the Aristotelian concept of violent motion. The same method of association, however, could not be applied so simply with regard to the curvilinear course: Tartaglia describes it as an arc of circumference, shown in the diagram (Fig. 2.4). Lacking further conceptual tools, Tartaglia hypothesizes that there is also a violent motion when the trajectory of the projectile follows the arc of circumference. Based on this hypothesis, it was necessary, moreover, to conclude that the projectile continued slowing down until the point at which the downward rectilinear natural motion began. Despite the fact that this interpretation of the trajectory obviously contradicted what could be observed, Tartaglia did not have the appropriate theoretical tools to explain this curvilinear section quantitatively. Faced with the hypothesis of a possible combination of motions, Tartaglia nevertheless specifies:
Assuming (as the opponent says) the [body] could travel some part with violent and natural motions mixed together, which may be part CD, it follows therefore that the mentioned body, while going from point C to point D, increases its velocity according to the ratio by means of which it shares a natural motion (because of the first proposition). Likewise, it decreases its velocity according to the ratio by means of which it shares a violent motion (because of the third proposition). It is absurd that the mentioned body increases and decreases its velocity at the same time.20
The sixth and last proposition of the first book returns to the possible practical applications of the novelty of ballistics and thus to the analysis of the effect of the shot on the target or “resistant body:”
Sixth proposition.
All resistants are less damaged by an equally heavy body that is violently ejected through the air at the instant that distinguishes the violent from the natural motion than at any other place [on the trajectory].21
In line with the concept of violent motion and natural motion outlined in the preceding propositions, the instant at which the violent motion ends, which coincides with the instant at which natural motion begins, is considered from both conceptual perspectives to be the moment at which the motion is at its slowest. Finally, as stated in the suppositions, the moment of least velocity is implicitly associated with the least effect.
2.3 The Second Book
The second book is the one in which Tartaglia develops his mathematical treatment of the trajectory of projectiles. He concludes by relating this to those aspects relevant to the bombardiers of the period, namely the range of shots and their effect on the target.
The first three “definitions” describe the characteristics of the rectilinear and curvilinear motions of which the trajectory is composed. From the fourth to the seventh definition, he establishes a geometric system of reference on the basis of which the parameters of the trajectory can be calculated, i.e. the horizon and the perpendiculars towards and over it. From the eighth to the fourteenth (and last) definition, the entire portion of the trajectory accomplished by violent motion is analyzed. First he provides the information that allows the angle of elevation of “transit” above the line of the horizon to be calculated, and in the tenth definition22 he specifies how an angle of elevation of 45 degrees is established. He then identifies by definition the rectilinear segments of the trajectory depending on the greater or lesser angle of elevation with respect to 45 degrees, thereby creating the conditions to identify similar trajectories on the basis of the angle of elevation. Finally, the last definition creates the preconditions for quantifying the violent motion:
Fourteenth definition.
The length of a transit, that is, of the violent motion of an equally heavy body, is the interval along a straight line from the beginning to the end of the violent motion [(Fig. 2.5)].23
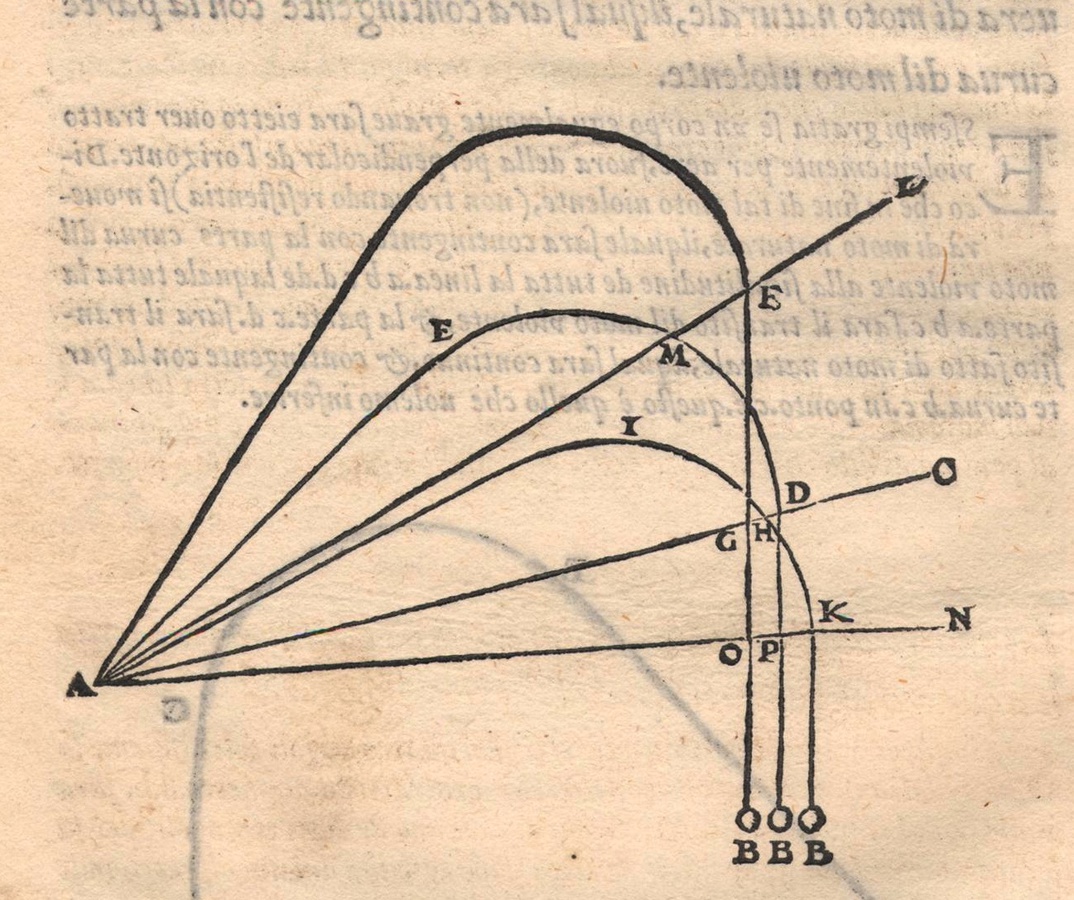
Fig. 2.5: Graphic representations of the “distance of transit” (distantia del transito) with reference to three different angles of elevation. “The distance of transit” is represented by the straight line which joins the initial and final point of the violent motion. From Tartaglia 1558, second book, 11v.
Tartaglia considers both the rectilinear and the curvilinear motion. He suggests drawing a straight line from the starting point of the motion to the point where it ends and the natural motion begins, referred to by Tartaglia as “transit” (transito).24 This expedient makes it possible to reduce the trajectory to the one that could be deduced from Aristotelian dynamics, namely to a composition of two straight lines joined with each other so as to create an angle. This subsequent step of abstraction salvages the validity of the physical observation that the trajectory is not actually constituted of two straight lines, but at the same time allows measurements to be taken and is fundamental to considering the effect of the motion. The definition of “transit” is, in fact, directly related to the fourth supposition of the second book:
Fourth supposition.
The farthest effect, produced by an equally heavy body [that moves] with violent motion on whichever plane or whichever straight line, is the one that happens precisely on that plane or on that line (if it is ejected or thrown by the same moving power).25
By means of this supposition, Tartaglia confines the trajectory to the conceptual framework of Aristotelian dynamics, while simultaneously adapting it to meet the demands that had motivated his own theoretical research. The thirteenth definition and the fourth supposition “level out” the trajectory, so to speak, so as to be able to quantify it. Nevertheless, it was not the mere lack of mathematical procedures which made it impossible for Tartaglia to analyze the dynamic aspects of the curvilinear motion. It was also the utilitarian aspect from which his Nova scientia was born that led him to analyze those aspects which were of real use to the bombardier. As will be seen in the sixth section of this work, during the period in which Tartaglia wrote, the technological development of artillery had already led to the replacement of the first generation of heavy firearms such as the bombard, for which an analysis of the effects of natural motion would have been far more relevant. As will now be shown more clearly, the birth of the science of ballistics was not directly correlated to the diffusion of firearms in general, but to the diffusion of those firearms that began to be produced in the sixteenth century, and for which an analysis of the “transits” was necessary.
Tartaglia was fully aware that he was forcing the trajectory he could observe into the formal instruments at his disposal. Even without considering the straight line which joins the start of the motion with the point at which violent motion changes to natural motion, Tartaglia, as has already been mentioned, was aware of the fact that the real trajectory also did not correspond to the trajectory made up of two straight lines joined up by an arc of circumference. In his explanation in the second supposition, Tartaglia admits:
Nevertheless, that part [of the transit] that is not perceived as being curved is assumed to be straight, and that part that is evidently curved is assumed to be part of the circumference of a circle, as this [assumption] does not influence the argument.26
Tartaglia’s association of the curvilinear line of the first part of a trajectory with a straight line is generally known. It is worth adding here that Tartaglia considers the second part of the trajectory, i.e. the curvilinear part, as merely an arc of circumference, probably for geometrical simplicity. Tartaglia justifies this expedient by declaring that the association of the two curved sections with simple and well-known geometrical forms does not yield any major errors in the theoretical treatment.
Following a series of purely geometrical considerations that link the third supposition to the first three propositions of the second book, Tartaglia arrives at a quantitative analysis of the curvilinear section, distinguishing between shots from a zero-degree angle of elevation (fourth proposition), shots from a greater angle of elevation (fifth proposition, “elevated transits” or transiti elevati), and shots from a lower angle of elevation, such as those which were necessary when the pieces of artillery were positioned at a higher point than the position of the target (sixth proposition, “oblique transits” or transiti obliqui).
The following last propositions of the book, from the seventh to the ninth, along with their associated corollaries, are the first conclusions of a general nature in the history of modern theoretical ballistics. The seventh proposition provides the theoretical foundation needed to assert the universal value of the propositions that follow and specifically relate to ballistics:
Seventh proposition.
All transits, that is, violent motions of equally heavy bodies, big and small, equally elevated above the horizon, or equally oblique, or moving along the plane of the horizon, are similar and consequently proportional to each other. Their distances are similar and proportional to each other.27
This implies that each conclusion made with reference to a particular trajectory, be it empirical or theoretical, is also true with relation to any other trajectory, provided that the angle of elevation is the same. Empirically, the validity of this generalizations is maintained as long as the moving power and the other material conditions remain the same.
The eighth proposition represents the theoretical foundation upon which modern ballistics has developed since Tartaglia’s time:
Eighth proposition.
If the same moving power ejects or throws equally heavy bodies, which are similar and equal to each other, violently through the air but in different manners, the one [equally heavy body] that accomplishes its transit at an elevation of 45 degrees above the horizon produces its effect farther away from its beginning and above the plane of the horizon than [if it were] elevated in any other way.28
The greatest range of a shot is achieved at an angle of elevation of 45 degrees above the line of horizon. As has been mentioned, Tartaglia never provided a table that set out the correlations between the range of a shot and every single angle of elevation, which he had promised in the incipit to do in the fourth book. Nevertheless, he does offer us such a correlation in the dedicatory letter (and not in his lengthy and complex explanation of the eighth proposition):
Then, using natural arguments, I found that the range of the above-mentioned shot elevated at 45 degrees above the horizon was ten times the straight transit of a shot made parallel to the plane of the horizon, which is said by the bombardiers shooting at the blank point.29
Tartaglia does therefore provide just one single correlation quantified between two different angles of elevation, and thus between point “one” and point “six” on the quadrant. The arc of the quadrant was traditionally divided into twelve points at angles of equal intervals, as in the case of the instrument described by Tartaglia.
Finally, Tartaglia adds the ninth proposition, which would leave any reader perplexed were it not possibile to consult another of his works.30 The ninth proposition does in fact focus on determining the relationship between the straight segment of the transit of a projectile thrown through the air at a 45-degree angle of elevation, and the same part of the trajectory but of a projectile thrown at a zero-degree angle of elevation. Tartaglia affirms that the length of the rectilinear segment of the trajectory of the projectile launched at a 45-degree angle of elevation is four times that of the same segment for a projectile launched at a zero-degree angle of elevation. In order to arrive at this result, Tartaglia formulates a lengthy and complex geometrical explanation which, however, does not refer to any possible practical application to the experience of the bombardier. As Gerhard Arend has observed, the ninth proposition actually refers to the relation between the length of the rectilinear segment of the section of the trajectory where there is violent motion and the force of the piece of artillery, an idea developed by Tartaglia in the first book of the Quesiti.31
2.4 The Third Book
The third book, which has been translated in this work for the very first time, is the most voluminous among the three published by Tartaglia. Certainly, the third book is not the part of the Nova scientia that presents the most interesting theoretical developments of Tartaglia’s science, but it is only by means of a deep analysis of this text that Tartaglia’s attempt to connect practical and theoretical knowledge can be truly understood and appreciated.
The goal of the third book is to present instruments for measuring distances by sight. Although such instruments are applicable for the measurement of distances in many circumstances, Tartaglia coherently takes into consideration only those cases which could be of interest for the artillerymen of his time, such as, for instance, the diametral distance between the observer—the artillerist—and a point located at a higher position in front of him, which could be, for instance, the stronghold of a bastion. The book is constituted of five definitions and twelve propositions,32 that is, no supposition (postulate) and no common sentence (axiom) are contained. The definitions define the system of reference first with reference to the line of the horizon (the ground) in order to univocally determine the distances that have to be calculated. These are the above-mentioned diametral distances; the height, which is the line that perpendicularly joins the point to be targeted with the ground; and the horizontal distance, which joins the observer with the point where the height touches the ground (Fig. 2.6). The first four propositions deal with all of the preconditions needed in order to construct an instrument to measure by sight. These include practical methods to check whether rulers are perfectly straight, and set squares and quadrants correct. Proposition six finally describes the building procedure of the instrument in detail.

Fig. 2.6: Graphic descriptions of the method for measuring heights using the quadrant proposed by Tartaglia. From Tartaglia 1558, third book, 26r.
The purpose of the instrument is declared immediately in the heading of the proposition:
Sixth proposition.
I would like to manufacture an instrument for myself that I can use to level the ground and to analyze it by means of sight and [to calculate] the heights, widths, depths, and diametral and horizontal distances of perceptible objects. This instrument should also be easily usable to investigate the variety of shots of each piece of artillery and, similarly, of each mortar.33
In the heading Tartaglia also points to the fact that such an instrument is basically the same as the bombardiers’ set square presented in the dedication letter, although the practical use of the instrument for this purpose is not repeated in the third book. In the second expanded edition of 1550, Tartaglia adds a relevant text to proposition six—Correction of the author—by means of which he suggests some constructional alternatives that aim to improve the precision of the instrument, a sign that the precision of targeting the artillery had also improved in the thirteen years that separated the first from the second edition. The instrument suggested by Tartaglia was by no means an original achievement at his time. Similar instruments were already widely circulating around the half of the earlier century. Particularly noteworthy are the striking similarities between Tartaglia’s instrument suggested in proposition six and the Quadratum geometricum designed and built by Georg von Peuerbach, probably around 1454, the textual description of which was first published in Nürnberg (Fig. 2.7).34
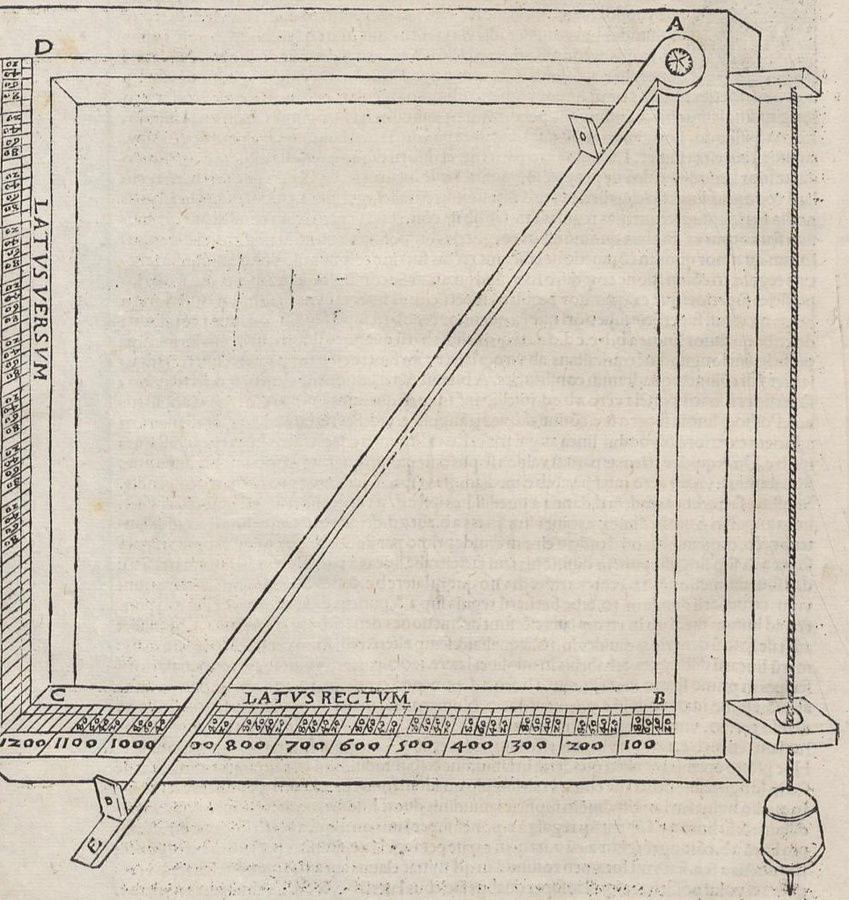
Fig. 2.7: Georg von Peuerbach’s Quadratum geometricum, a predecessor to the instrument and very similar to the one described by Tartaglia. From Peuerbach 1516.
Propositions seven to ten, finally, show how to use the instrument to calculate the different sorts of distances needed. As is usual for a deductive geometric system, the propositions build upon each other. Proposition seven shows how to determine the flatness of the ground, proposition eight shows how to measure the diametral and the horizontal distances, proposition nine has the same scope as its predecessor but with the difference that it takes into account the possibility—very real—that the observer, that is, the artillerist, cannot move from the place where he actually stands to one where the measurement procedure would be easier to perform.35
In 1550 Tartaglia introduced some additions to the explanatory text of proposition nine as well. In this case, too, Tartaglia’s goal was to indicate procedures to improve the precision of the measurements. Finally, proposition ten reproduces a particularly realistic situation for the bombardier of his time:
Tenth proposition.
I would like to artificially measure the height of a perceptible object, whose lowest point or fundament cannot be seen and to which one cannot go. By means of the same operation, I would like to investigate the hypotenuse or diametral distance of such a height and also the horizontal distance, that is, the distance between my eye and the point where the line of the horizontal distance meets that height, although this point cannot be seen. Similarly, I would like to investigate the length of the line from my feet straight toward the lowest point or fundament of that height, although it cannot be seen.36
As the picture clearly shows, Tartaglia examines the case in which the point where the height meets the ground cannot be reached or seen directly, but, in Tartaglia’s terms, “when the mind’s eye is required.”

Fig. 2.8: Graphic description of the method for measuring heights by means of a surveying set square when the point of conjunction between the line that joins the object to be observed with the ground, and the line between this last point of the observer himself, cannot actually be seen or reached. From Tartaglia 1558, third book, 29r.
The procedure described in proposition ten is particularly complex and laborious (Fig. 2.8). The instrument Tartaglia explains how to operate is one he built himself, and therefore he relates many characteristics of both its construction design and its use that depend on the manufacture and the choice of the materials. Many of these aspects are obviously not described completely, as for instance, the shape of the base of the instrument on which its perpendicularity depends, which varies for the different sorts of ground on which an artillerist or a surveyor had to work. In proposition ten Tartaglia reaches a point in his argument beyond which he cannot proceed, because the description of all the possible expedients cannot be offered in written form:
It should also be added that I could find out the mentioned hypotenuses as well as all other measurements by means of other methods, which are easier, especially for those who are not able to calculate the square root and are not practiced with numbers. However, as these methods are difficult to describe by means of writing, I will not discuss them.37
Technology clearly evolved by embedding in the instruments—and thus in its products—an increasing number of aspects of knowledge involved in these practices, which depended on human skills. In the sixteenth century many of these expedients were not codified, either in an artifact or in a text. The 1537 edition closes with the words just quoted.38 However, in 1550 Tartaglia added one folio to the text of the same proposition in order to describe some further expedients, and, in particular, to show how to make sure that the visual apparatus of the surveying instrument is always at the same altitude with respect to (one would say today) sea level. This was possible thanks to additional specifications concerning the construction of the base and the pole supporting the instrument.
The texts of propositions seven through ten are difficult to read because they describe not only all steps of the measurement techniques, but also the geometric reasoning upon which such procedures were based. In other words, the validity of the described procedures was demonstrated geometrically on a theoretical level. In no other section of the Nova scientia does the tension between practical and theoretical knowledge emerge in such an evident manner as in this third book. Tartaglia eventually becomes aware of the fact that one of the two categories of potential readership of his book, the artillerymen, while eager for a more stable theoretical foundation of their activity, lacked the fundamental knowledge, such as Euclidean geometry, needed to fully understand Tartaglia’s demonstrations. The result is, first, that each subject is declared in many different ways, making it even more difficult to understand because of Tartaglia’s limited narrative capacity and literary skill,39 and, second, that the texts ultimately include a terrific number of repetitions, probably in line with the didactic principles of the time that had persisted since antiquity (repetita iuvant).
Each measurement procedure is first described in terms of the practical steps to be followed in order to accomplish it. Either integrated with this description or following it, Tartaglia then furnishes a geometric demonstration, and often more than one, in order to refer to different definitions, postulates or propositions of Euclid’s Elements. Then, at least one example is furnished “in the frame of the practice of numbers,” and therefore involving arithmetics up to the use of the square root. This threefold description is then repeated according to the different situations in which the surveyor may find himself, for instance on uneven ground, or in a place where he cannot directly target by sight all the points needed to accomplish the measurement required.
The texts finally contain continuous but very specific references to the Elements of Euclid, so that any reader interested in so doing has the opportunity to move from the practice to its deepest theoretical foundations.
Finally, the last two propositions of the third book are the additions explicitly announced in the title of the second edition of 1550. With the help of these texts, Tartaglia describes another surveying instrument he designed. Proposition eleven relates very carefully how to build it and even some of its variants. This instrument, too, was just a variation of other surveying instruments widely circulating in Tartaglia’s time. However, being able to design a new device with some small changes was quite sufficient to improve the own professional image. In particular, the instrument is a dioptra to be used mainly on a horizontal position, but one that could also be reverted to a vertical position to be used similarly to the instrument described in the previous propositions.

Fig. 2.9: Graphic representation of the measurement technique realized by means of the dioptra designed by Nicolò Tartaglia and described in propositions eleven and twelve of the third book added in the second edition of 1550. From Tartaglia 1558, third book, 32r.
Footnotes
Tartaglia 1558, first folio (unnumbered), verso. In the 1558 print run, the numeration of the pages starts at the beginning of the first book. The frontispiece, the incipit and the dedicatory letter are not numbered.
Tartaglia 1546. With reference to the themes which Tartaglia promised to cover in the Nova scientia, but which were discussed only in Quesiti et inventioni diverse, see Arend 1998, 127–128.
Tartaglia 1558, second folio (unnumbered), recto. This quotation is from page
With regard to the chronology of the diffusion of the quadrant among bombardiers, see Schmidtchen 1977, 139–161.
Codex 51 1410 ca.. See also Essenwein and von 1873.
For an in-depth analysis of the relation between Aristotele’s dynamics and its use in Tartaglia’s work, see Koyré 1960. For an overview on how Aristotelian dynamics was received and transformed within the framework of early modern practical knowledge of artillery men, see Büttner et.al. 2003. See also Besana 1996.
Tartaglia 1558, first book, 2r. This quotation is from page
The translation of the present work does not follow Drake’s translation of this fundamental term as “uniformly heavy body.” Although the choice of “uniformly” rather than “equally” renders the meaning in a more effective way given the actual use of the concept of “uniform” in physics, the rendering with “equally” points to the evident difficulty scholars of the sixteenth century had with finding and inventing an appropriate terminology for their theoretical and mathematico-physical speculations. As all of Tartaglia’s work exudes this profound tension between ideas and the way to express them, the use of the word “uniformly” would give the wrong impression of established scientific discourse.
Tartaglia 1558, first book, 1r. This quotation is from page
Tartaglia 1558, first book, 1r–1v. This quotation is from page
Tartaglia discusses the works of Avicenna and Averroes in the first definition of the first book: Tartaglia 1558, 1r. The following editions have been identified as those used by Tartaglia: Avicenna 1507 and Aristotle and 1520.
In his commentary of the fourth book of Aristotle’s De caelo, Averroes considers the elements as constituted of particles, precisely with the shape of triangles. Depending on the density of those triangles and due to the admitted existence of interstitial vacuums, a certain large amount (volume) of air can result in being heavier than a different amount (volume) of water. The reading of Averroes’ text should not be confused with an argument based on the idea of specific weight. His argument seems rather to draw the consequences of the theory of elements as described in the framework of pneumatics, for instance by Hero of Alexandria. In text 29 in particular, Averroes clearly states that air is a heavy element and only fire is characterized by the quality of lightness. For text 29, see Aristotle and 1520, 247–249. For an introduction to Averroes’ commentary on De caelo, see also Endress 1995.
Especially because of the capacity of air to share the quality of humidity of water, over which air is displaced, air is considered by Avicenna to be an element more worthy of lengthier discussions than the others. Indeed, Avicenna seems to associate air with both lightness—when it shares the qualities with the element fire displaced over the air itself—and heaviness, when it shares the quality with the element of water beneath it. Avicenna’s argument is also certainly influenced by the experience and doctrines of pneumatics, according to which air is a body like water. Whether fire is an element that corrupts air, as according to Hero of Alexandria, and therefore qualitatively different from air and water, is an ancillary problem that not even Hero himself managed to work into his argument. It can only be speculated as to why Tartaglia considers this difference from the orthodox Aristotelian doctrine of the elements to be particularly relevant in the theoretical frame of his new science of ballistics. He may have welcomed this system as it allowed him to avoid discussing the effect of the medium, i.e. air, on the projectile while conceiving that the natural motion of such a medium is upward.
In the Aristotelian plenum, the speed at which an object falls obviously depended on the shape of the object in motion, whereas resistance to the medium being traversed needed to be considered. In this context, Tartaglia returns to medieval reflections regarding this interdependence, usually referred to as “gravitas ex figura.” For more details, see Arend 1998, 202–203.
Tartaglia 1558, first book, 3v. This quotation is from page
Tartaglia 1558, first book, 7r. This quotation is from page
Tartaglia 1558, first book, 7r–7v. This quotation is from page
Tartaglia 1558, first book, 7v. This quotation is from page
Tartaglia 1558, second book, 10r. Note that there is an error in the print of the 1558 print run with regard to the indication of the second and third book. “Libro primo” is indicated in the header of each page from the beginning all the way to the end of the entire work.
Tartaglia 1558, second book, 10v. This quotation is from page
Interestingly, while reading the 1558 print run used in the present work, it was striking to find the concept of ’transit’ used as a technical term. However, by comparing this edition with the first print run of the second edition of 1550 and with the first edition of 1537, it becomes clear that the univocal association of this word with such a specific meaning is probably an involuntary consequence of the editorial work of the typographer who published the 1558 text. See also Section 7.
Tartaglia 1558, second book, 11r. This quotation is from page
Tartaglia 1558, second book, 11r. This quotation is from page
Tartaglia 1558, second book, 16r. This quotation is from page
Tartaglia 1558, second book, 16v–17r. This quotation is from page
Tartaglia 1558, epistle, third folio (unnumbered), verso. This quotation is from page
Arend 1998, 129. It has to be noticed that for shots at a zero-degree angle of elevation, the rectilinear segment de facto coincides with the transit.
The third book of the 1537 edition contains only ten propositions.
Tartaglia 1558, third book, 22v. This quotation is from page
See Peuerbach 1516. See also Zinner 1968, 26–49.
“Ninth proposition. Without changing the position of where I am, I would like to know the height of a perceptible object when it is possible to move to its lowest point, that is, to its fundament and, by the same operation, I would like to know the hypotenuse or diametral distance of this height.” From Tartaglia 1558, third book, 25r. This quotation is from page
Tartaglia 1558, third book, 28r. This quotation is from page
Tartaglia 1558, third book, 29v. This quotation is from page
The sentence is not precisely the same, but with the same meaning.
According to Virginia Iommi Echeverría, Tartaglia’s insufficient literary skill is the main reason why his works failed to exert any significant influence in his own lifetime. For more details, see Echeverrı́a 2011. However, other studies convincingly show that Tartaglia indeed played a major role in the process of establishment of vernacular as scientific language. For more details, see Piotti 1997, 271.
