6.1 Benedetti as an Astronomer
Benedetti’s astronomical considerations are not systematic. They are scattered throughout the volume in different sections. In spite of the difficulty of ordering them and obtaining an overview, they were very much appreciated among his contemporaries. Apart from Kepler’s
In fact, I sometimes saw that Venus illuminated in a rather sensible manner that part of the Moon that was most distant and opposed to the Sun, although the Moon is by far more distant from Venus’s circuit than the comet. I remarked that the Venicepatrician Giovanni Battista Benedetti, the most excellent philosopher and mathematician, noted something similar in that erudite work which he wrote on mathematical and physical speculations. At the end of an epistle to a certain Savoy baron, Filiberto , he says: “[…] that the part of the Moon which is deprived of the Sun’s light is sometimes partially illuminated by Venus’s light. I observed this often and showed it to many people.”1
Brahe
A second long direct quotation of Benedetti can be found in Brahe’s
Here follows the epistle which I referred to. It is taken from the aforementioned book by [Giovanni] Battista Benedetti alongside the demonstrative diagrams offered by the same author. Afterwards I will consider others, who discussed that star [i.e., the nova of 1572] in an extraordinarily incompetent manner. This [quotation from Benedetti] (as mentioned) will cast light on these issues through a synthetic and wise geometrical truth, so that no significant doubt will survive.5
Another reader of the Diversae speculationes was the English scholar of magnetism William Gilbert
Benedetti’s treatment of astronomical matters ranges from the calendar reform to the nova of 1572, sundials, and astrology. We would like to focus on a special issue: Benedetti’s defense of ephemerides, Defensio ephemerides, and the quarrel that motivated its writing. This defense of ephemerides figures as one of the epistles of the Diversae speculationes. It is the Latin translation of an Italian letter, Intorno ad alcune nuove riprensioni… contra alli calculatori delle effemeridi (Letter in the Form of a Discourse… Addressed to the Illustrious Mr Bernardo Trotto Concerning Some New Criticism and Corrections against the Ephemerides Calculators, Turin, 1581), addressed to Trotto
6.2 The Controversy over the Reliability of Ephemerides
The ephemerides controversy began with the publication of Altavilla’s
Altavilla
The Animadversiones were soon followed by a second publication in Italian: Breve discorso intorno gli errori dei calculi astronomici (Brief discourse on the mistakes of astronomical calculations, 1580). A poem by a certain Francesco Onto
In his second publication, the Discorso, Altavilla
This attack on the reliability of astronomical computations and astrology provoked negative reactions both at the university and at the court. Altavilla
Soon after Altavilla’s
Moreover, he accuses Altavilla
Yet, he [Altavilla] dared too much, seeking to reprimand so many talented ancient and modern men who, as is required by diligent observers of the heavens, checked with their own eyes these appearances of Mars as well as of the other [planets]. From those [observations], they were forced to “imagine” such a large [Martian] epicycle. By contrast, he has never observed the motions of either this or any other planet, but rather limited himself to look at what is written in the ephemerides. In fact, if he had at least said that he observed Mars’s journey for a certain period, and that he found that the others’ opinion was false, he would have at least given some “color” to his opinion. In my assessment, however, if he had made an observation of the path of Mars, he would not have held the contrary view. In fact, the truth is the following: in every revolution of its epicycle, Mars in the lower part of its epicycle always stays many months (six or seven, or more) in a twelfth [duodecatemerio] of the zodiac. I observed this many times, for instance, in the years 1565 and 1566. First, consulting Stadius’s ephemerides, I found that Mars would finish its retrograde motion on about 12 January 1566, in 16° of Gemini, and that, equally, Mars would be in the same place on the last day of August 1565, before it began its retrograde motion. Second, I found that, after that retrograde motion, on 11 April 1566, Mars would be in 16° of Cancer, so that it would take [Mars] seven months and eleven days [to move] those thirty degrees, from 16° of Gemini to 16° of Cancer. After these computations, I took the instruments and got ready to make a test. And I found that the last night of August of the year 1565 Mars was in the aforesaid 16° of Gemini, as Stadius had noted. I then made observations every week, in order to see the retrograde motion, and I saw that, at about the end of October, the [planet] began its retrograde motion and that retrograde motion lasted until January (or about January) 1566. I later observed the position of that planet on 11 April, and I found it in 16° of Cancer, that is, the place where Stadius had located it. Thus, my experience confirmed Stadius’s computations and I found that he was not mistaken. In the same manner, everybody can ascertain the truth every two years by carrying out observations.21
Benedetti thus demonstrated not only the theoretical incompetence of his opponent, but also his lack of empirical verification. Altavilla’s
As to the difference between Leowitz’s
As a courtier expert of mathematics, Benedetti defended the validity of some astrological figures that Altavilla
Altavilla
6.3 The System of the World
Benedetti did not limit himself to considering astronomy from a computational point of view, but also expanded on cosmological aspects. The epistle “De fine corporum coelestium, et eorum motu” (On the Aim of Celestial Bodies, and their Motions),27 addressed to Pingone
[…] this will hardly be believed by those who embrace the doctrine of Aristarchus of Samosand Nicolaus Copernicus . Following their approach it is impossible to make them believe that the rest of the universe has no other aim than to rule over this center of the lunar epicycle [the earth] (to use their way of speaking).29
Although he speaks in the third person, as if he were reporting the views of someone else, these are his own views. He is inclined to accept the Copernican
Ptolemy’sobjections are not valid for them [astronomers who assume that the earth moves]. As they say, every part maintains the nature of the whole, apart from the fact that the air and water circumscribing the earth receive the same natural impulse of motion [impetum motus]. This is slower the further the air is distant from the earth. According to the same doctrine, there is no necessity that the place of the fixed stars has (either convex or concave) superficial boundaries.34
According to this passage, the air close to the earth is transported by the motion of the planet and slows down the more it is distant from it. The fixed stars are placed in a motionless air whose place (locus) has no boundaries, either convex or concave.
In a letter to the courtier Capra
Furthermore, Benedetti rejects the existence of material spheres with the role of transporting the planets:2
That you do not accept that distinction of spheres, which was well-established in the past, but rather that you believe that the whole is a continuum accommodating the stellar bodies, this is not new. In fact, some philosophers of solid doctrine were of the same opinion.37
The motion of celestial bodies is accompanied by that of transparent bodies similar to vapors (fumi). Their motion is the cause of the apparent sparkling of the most distant stars.38 The sparkling of the new star in Cassiopeia in 1572 bears witness to its great distance above the moon, which Benedetti also demonstrates through geometry.39
One of the books of the Diversae speculationes entails a discussion and a refutation of Aristotelian
Aristotledid not consider that one could affirm the same about the Earth as seen from great distance. There is no doubt that, even if the Earth had the light of the Sun and somebody tried to observe it from the eighth sphere, he would not be able to perceive it. In fact, those celestial bodies that are said to be of the first magnitude and that are believed to be more than a hundred times bigger than the Earth look just like points.40
Benedetti supports the plurality of worlds as well (Minus sufficienter explosam fuisse ab Aristotele
6.4 Appendix: An Assessment of Benedetti’s Horoscopes (by Günther Oestmann)
For the recalculation of a historical horoscope, the same methods and means the author had at his disposal must be employed, that is, the use of modern parameters or tables is not allowed.42 In the following disposition, planetary positions are rendered in ecliptic longitude (degrees ; minutes) for each zodiacal sign (0–30°), geographical coordinates likewise in degrees ; minutes, and time in hours ; minutes. Latitude is denoted as φ.
6.4.1 Nativity Cast by Benedetti for Duke Carlo Emanuele I of Savoy
January 11, 1562 (Julian date), 16;23 p.m., φ = 45°; Planetary positions according to the Prutenicae Tabulae by Erasmus Reinhold(1551).

Fig. 6.1: The horoscope cast by Benedetti for Duke Carlo Emanuele I of Savoy. This was calculated with the Prutenic tables, as transcribed by
Carlo Emanuele I
The geographical coordinates of the nearest town to Turin
| Planets | Original Source | Recalculation |
|---|---|---|
| Sun | 1;27 Aq | 1;27 Aq |
| Moon | 29;09 Ar | 29;16 Ar |
| Saturn | 28;54 Ge retrograde | 28;55 Ge |
| Jupiter | [missing] | 21;02 Ta |
| Mars | 18;42 Ar | 18;41 Ar |
| Venus | 0;58 Cp | 0;58 Cp |
| Mercury | 15;48 Cp retrograde | 15;48 Cp |
| Lunar node (asc.) | 15;19 Aq | 15;16 Aq |
Tab. 6.1: Planets
Tab. 6.1: Planets
| Houses (Regiomontanus |
Original Source | Recalculation |
|---|---|---|
| X | 10;23 Li | 10;16 Li |
| XI | 5;05 Sc | 4;59 Sc |
| XII | 24;35 Sc | 24;32 Sc |
| I | 15;57 Sa | 15;54 Sa |
| II | 17;11 Cp | 17;07 Cp |
| III | 2;05 Pi | 1;58 Pi |
| Lot of Fortune (Night) | 18;15 Vi | 18;05 Vi |
| Lot of Fortune (Day) | 13;39 Pi | 13;43 Pi |
Tab. 6.2: Houses
Tab. 6.2: Houses
The Lot of Fortune (Pars Fortunae; named for the Roman goddess of luck and wellbeing) is calculated in diurnal charts by subtracting the ecliptic longitude of the sun from the longitude of the moon. Then the difference is added to the longitude of the Ascendant: Lot of Fortune = Ascendant + Moon – Sun. For nocturnal charts, the calculation is Ascendant + Sun – Moon.
Although this is a night-time birth chart, Benedetti has marked the Lot of Fortune for night and day.
The sign and degree occupied by the moon when crossing the ecliptic from southern to northern latitude is the ascending node (Caput Draconis). When the moon is moving in the opposite direction (crossing the ecliptic from north to south), the point of intersection is called the South Node (Cauda Draconis). The nodes are not fixed, but have a retrograde movement (a complete revolution of the nodes in the ecliptic takes 6798 days/18.61 years). To both points (which are important in the interpretation of a chart), the strength of a planet has been assigned. The Dragon’s Head is considered beneficial, the Dragon’s Tail malefic. (In Hindu astrology, the ascending node is called Rāhu and the descending node Ketu; both are considered malefic planets.44.)
Benedetti forgot to inscribe Jupiter. Apart from this flaw everything has been calculated accurately.
6.4.2 Revolution or Solar-Return Horoscope
January 21, 1592 (Gregorian Date), 23 h 15 m 30 s p.m., φ = 45°.
Geographical coordinates of Turinaccording to Petrus Apianus in Cosmographicus liber (1533): f. XXXVr – Toledo 9;04 East of Porto Santo ; f. XLIIr –Turin 30;30 → 21;26 East of Toledo (the reference meridian of the Alfonsine tables).
| Planets | Original Source | Recalculation (Alfonsine |
Recalculation (Prutenic tables) |
|---|---|---|---|
| Sun | 1;27 Aq | 2;08 Aq | 1;12 Aq |
| Moon | 9;27 Ta | 11;20 Ta | 8;12 Ta |
| Saturn | 7;29 Ca retrograde | 10;30 Ca | 7;30 Ca |
| Jupiter | 11;44 Sa | 10;31 Sa | 11;42 Sa |
| Mars | 3;05 Ar | 4;23 Ar | 3;00 Sa |
| Venus | 25;09 Sa | 23;00 Sa | 25;08 Sa |
| Mercury | 9;36 Aq | 5;43 Aq | 9;25 Aq |
| Lunar node (asc.) | 4;54 Ca | 5;05 Ca | 4;53 Ca |
Tab. 6.3: Planets
Tab. 6.3: Planets
| Houses (Regiomontanus |
Original Source | Recalculation I (φ = 45;00; 23;15 p.m.) | Recalculation II (φ = 45;00, 23;17 p.m.) |
|---|---|---|---|
| X | 21;00 Ca | 20;30 Cp | 20;59 Cp |
| XI | 1;00 Aq | 10;36 Aq | 11;11 Aq |
| XII | 17;00 Pi | 16;26 Pi | 17;18 Pi |
| I | 10;49 Ta | 9;56 Ta | 10;43 Ta |
| II | 15;00 Ge | 14;36 Ge | 15;08 Ge |
| III | 5;00 Ca | 4;18 Ca | 4;45 Ca |
| Lot of Fortune (Day) | 18;49 Le | 16;55 Le | 17;44 Le |
Tab. 6.4: Houses
Tab. 6.4: Houses
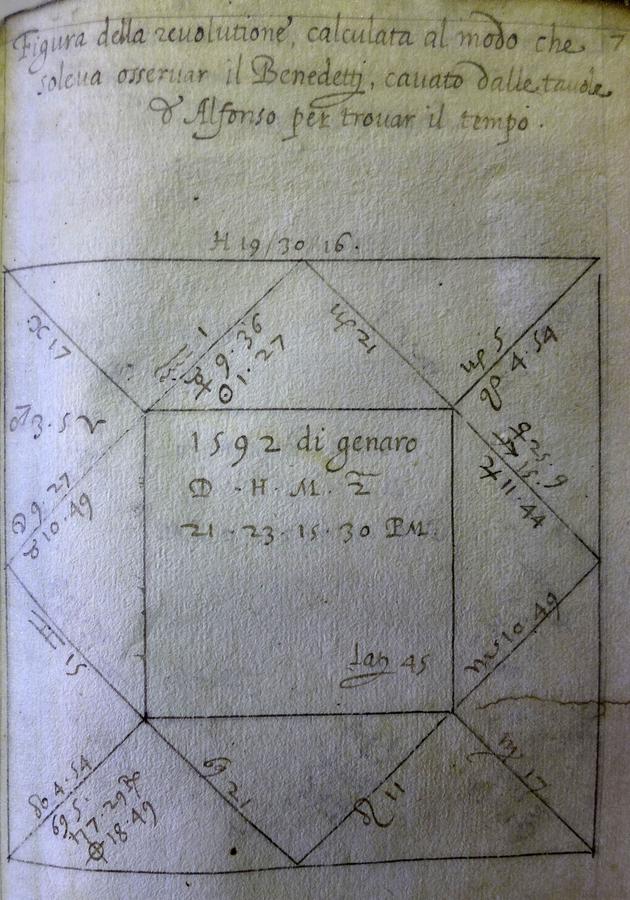
Fig. 6.2: Benedetti’s horoscope for Carlo Emanuele I, calculated with the Alfonsine tables, as transcribed by Cristini in Revolutione trentesima prima (1592), f. 12r. (Biblioteca Nazionale Universitaria di Torino, coll. N VII 10)
The second of Benedetti’s horoscopes to be considered is also taken from Bartolomeo Cristini
This is a chart constructed for the moment in which the sun returns to the degree and minute of its longitude at nativity (i.e., transiting the position of the “natal” sun) for the respective location. A revolution horoscope indicates the course of events during the ensuing year.
Contrary to Benedetti’s caption (Figura della revolutione […] cavato dalle tavole d’Alfonso
It is noteworthy that minutes for an arc are only provided for the first house (i.e., the ascendant). For the other cusps, only whole degrees are noted. Benedetti simply cut off the minutes, which was a common rounding procedure at his time.
6.4.3 Natal Horoscope of Giovanni Battista Benedetti
August 14, 1530 (Julian Date), 13 h 13 m p.m., Venice; planetary positions according to the Alfonsine tables. Geographical coordinates of Venice according to Petrus Apianus (1533): Toledo 9;04 East of Porto Santo (f. XXXVr); f. XLIIr: Venice 32;30, Latitude φ = 44;50 → 23;26 East of Toledo (the reference meridian of the Alfonsine tables).
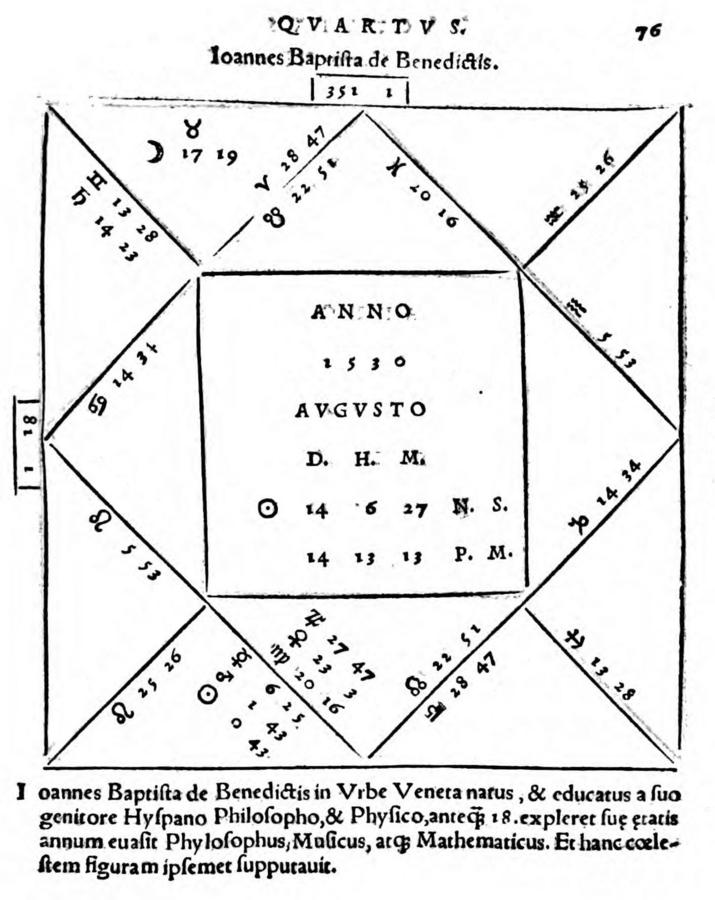
Fig. 6.3: Benedetti’s own horoscope, detailed in Luca Gaurico’s Tractatus astrologicus (1552, f. 76r). (Bayerische Staatsbibliothek)
| Planets | Original Source | Recalculation |
|---|---|---|
| Sun | 0;43 Vi | 0;42 Vi |
| Moon | 17;19 Ta | 15;02 Ta |
| Saturn | 14;23 Ge | 14;23 Ge |
| Jupiter | 27;47 Vi | 27;46 Vi |
| Mars | 1;43 Vi | 1;45 Vi |
| Venus | 23;03 Vi | 23;02 Vi |
| Mercury | 6;25 Vi | 6;25 Vi |
| Lunar node (desc.) | 22;51 Ar | 22;52 Ar |
Tab. 6.5: Planets
Tab. 6.5: Planets
| Houses (Regiomontanus |
Original Source | Recalculation |
|---|---|---|
| X | 20;16 Pi | 20;14 Pi |
| XI | 28;47 Ar | 28;36 Ar |
| XII | 13;28 Ge | 13;17 Ge |
| I | 14;34 Ca | 14;23 Ca |
| II | 5;53 Le | 5;46 Le |
| III | 25;26 Le | 25;23 Le |
Tab. 6.6: Houses
Tab. 6.6: Houses
Apart from the moon’s position (which is about 2° off) the horoscope is correct. In all three horoscopes the houses have been constructed according to the so-called “rational method,” commonly—but erroneously—attributed to Regiomontanus
Footnotes
Brahe 1919, 172: “Veneris enim Stella, visa est mihi aliquando eam partem Lunae, quae a Sole aversa erat, et ipsi obiecta, satis sensibiliter illuminare, utut Luna longe remotius a Veneris circuitus distiterit, quam Cometa. Simile quid Ioannem Baptistam Benedictum, Patricium Venetum Philosophum et Mathematicum inprimis excellentem, animadvertisse reperio, in erudito illo Opere, quod de Mathematicis et Physicis speculationibus inscripsit. Sic enim in fine Epistolae, ad Baronem quendam Sabaudarum Philibertum scribens, ait: ‘[…] quod pars Lunae lumine Solis destituta, a lumine Veneris aliquantulum illustratur, quod ego saepe vidi, et multis ostendi.’”
Brahe 1916, 251: “Nunc igitur epistolam, quam pollicitus sum, subiungam, verbotenens e praedicto Baptistae Benedicti libro desumptam, una cum demonstrationum delineationibus, quas ipse author assignavit. Deinde ad caeteros qui de hac stella nimis incompetenter, sententiam tulerunt, calamum dirigam. Ex quo (uti dixi) haec adeo succinte et scite geometricam veritatem redoleant, ut nullum, quod alicuius sit momenti, super esse queat, dubium.”
Gilbert 1651, 173: “Luna maculas quasi ostendit substantiae et peripheriae differentia: ita Tellus erga Lunam maculas repraesentat, terrarum continentium minus relucentium; aquarum vero et Oceani, propter laeviorem et luminis apprehensivam naturam magis splendentem. […] Non enim maculae Lunae existunt a partibus Lunae magis perspicuis, ut Iohannem Benedictus contendit, in quibus lumen non reflexum sed penetrans nobis occultatur.” See Pumfrey 2011, 193–203.
Section 6.2 is a revision of Omodeo 2014a, chap. 3.8–9 and chap. 6.3 of Omodeo 2014a, chap. 4.7.
This Benedetto Altavilla could be the same person involved many years later, in 1606, in a gunpowder plot in Venice; he pretended to have discovered it by astrological means and was tortured by the Venice authorities in order to obtain information about the perpetrators. Cf. Smith 1907, vol. 1, 364–365.
See Omodeo 2008b and Omodeo 2012a.
In Turin: Biblioteca Nazionale di Torino, coll. Q.V.191, and Biblioteca Reale di Torino, coll. G.25.12.
See Bonoli 2012, 49–55.
Benedetti 1585, 255: “[…] id etiam minus putabunt hii, qui opinionem Aristarchi Samii, et Nicolai Copernici sequuntur, quorum ratione fieri non potest, ut credant eius, quod ex universo reliquum est, alium finem non habere, quam regimen huius centri [Tellus] epicycli Lunaris, ut illorum more loquar.”
The same thesis is presented in Benedetti 1585, 195–196.
Benedetti 1585, 255–256: “quae quidem omnia [phaenomena], cum simplici gyro terrae circa suum axem (ut dicunt) tolluntur, quod sufficit ad recipiendum lumen, et influentias illorum corporum.”
Benedetti 1585: “Rationes autem a Ptolomeo in contrarium adductae apud ipsos, nullae sunt, quia quaelibet pars (ut inquiunt) retinet naturam totius, praeterquam quod aer, et aqua, quae ipsam terram circundant, plane eundem naturalem impetum motus obtineant, qui tanto lentior est, quanto longius distat aer, ab ipsa terra, secundum etiam talem opinionem, nulla necessitas, ut locus fixarum terminaretur aliquibus superficiebus, convexa scilicet, et devexa.”
Benedetti 1585, 285–286, “De motu molae, et trochi, de ampullis, de claritate aeris, et Lunae noctu fulgentis, de aeternitate temporis, et infinito spacio extra Coelum, Coelique figura.”
For Benedetti’s correspondence with Patrizi, see Claretta 1862.
Benedetti 1585, 411: “Quod eam distinctionem orbium, quae iam invaluit, non teneas, sed putes totum esse quoddam continuum excipiens corpora stellarum, novum non est, nam nonnulli solidae doctrinae philosophi idem confuerunt.”
Benedetti 1585, in the section entitled “Disputationes de quibusdam placitis Arist[otelis],” n. 38: “Occultam fuisse gravissimo Stagiritae causam scintillationis stellarum,” 186: “Scintillatio ergo stellarum, neque aspectus nostri ratione, neque alicuius mutationis earundem stellarum, sed ab inaequalitate motus corporum diaphanorum mediorum nascitur, quemadmodum clare cernitur, quod si inter aliquod obiectum, et nos, aliquis fumus, qui ascendat, intercesserit, videbimus obiectum illud quasi tremere. Hoc autem tanto magis fiet, quanto magis distabit obiectum ab ipso fumo; unde admirationi locus non erit, si stellas fixas magis scintillare, quam errantes cernamus. Lumen stellae ad oculum nostrum accedens, perpetuo per diversas diaphaneitates penetrat, medio continuorum motuum corporum mediorum, unde continuo eorum lumen variatur, et hoc in longitudinis magis, quam in propinquis stellis apparet.”
Benedetti 1585, 197, “Disputatio XXXIX, Examinatur quam valida sit ratio Aristotelis de inalterabilitate Coeli: Aristo[teles] non consideravit, quod similiter de terra dici posset, quando ipsa ita eminus prospiceretur, imo absque dubio putandum est, quod si terra luce Solis praedita esset, et aliquis ipsam ab octavo orbe vellet videre, nullo pacto cerneret, cum sidera illa quae primae magnitudinis vocantur, et quae plusquam centies maiora ipsa terra putantur non nisi ut puncta videantur.”
Benedetti 1585, 195: “Si essent dicti mundi, eorum quilibet suum proprium centrum, suamque propriam circunferentiam haberet, terraeque et ignes haberent inclinationem ad centra circunferentiasque suorum mundorum.”
Here a convenient, unfortunately little-known computer program created by Peter Schiller especially for the needs of historians has been used. See Schiller 2001. There is not sufficient room here for a detailed analysis of the choice of appropriate historical parameters; for a concise description, see Oestmann 2002 and Eade 1984, 1–103.
For details, see Bilfinger 1888, 262–286 and Ginzel 1914, 94–96.
It was already known in the Maghreb in the eleventh century, see Kennedy 1996, 543. For a profound treatment of the history of house division, see North 1986, although the way this text coins new designations is awkward and may lead to confusion.
