Kapitel 3.2.1
Im ersten Kapitel des zweiten Traktats werden definitiones und grundsätzliche Positionen zur Frage nach der Geschwindigkeit einer Bewegung in Hinsicht auf deren Wirkung dargelegt. Zuerst legt Alvarus Thomas die Unterteilung der gleichförmigen und ungleichförmigen lokalen Bewegungen dar. Dann erfolgt eine quaestio, die sich mit der communis definitio gleichförmig ungleichförmiger Bewegungen nach dem Subjekt beschäftigt, gegen die er Argumente vorbringt.
Alvarus Thomas beginnt im Rückgriff auf Aristotelis, die Aufteilung der lokalen Bewegung zu diskutieren. Als erstes unterscheidet er die gleichförmige und die ungleichförmige lokale Bewegung. Die gleichförmige Bewegung wird folgendermaßen definiert:
„Die gleichförmige lokale Bewegung ist [eine Bewegung], in der in gleichen [Teilen] einer Zeit gleiche Räume durchquert werden, wenn die Ausdünnung und die Verdichtung abgezogen werden und auch die anderen kleinen Kleinigkeiten, deren Art und Weise dagegen wirkt, eine Veränderung des Raums oder [etwas], was nämlich nicht irgendein Raum ist. Denn es genügt ein wahrer oder ein vorgestellter Raum; zum Beispiel wenn ein Bewegliches in genau einer Stunde eine Meile durchschreitet und zwar im ersten verhältnismäßigen Teil der Stunde den ersten verhältnismäßigen Teil der Meile, im zweiten [Teil der Stunde] den zweiten [verhältnismäßigen Teil der Meile] und folgerichtig so weiter.“1
Die ungleichförmige lokale Bewegung wird dagegen so beschrieben:
„Eine ungleichförmige Bewegung aber ist, wenn in gleichen Teilen der Zeit nicht die gleichen Räume durchquert werden. Die übrigen [Gegebenheiten] bleiben gleich, und [zwar] nach Abzug der abzuziehenden [Dinge], wie wenn ein Bewegliches in einer Stunde genau eine Meile durchschreitet, und zwar in der ersten Hälfte ein Viertel [der Meile] und in der zweiten [Hälfte] drei Viertel [der Meile]. Eine solche Bewegung ist ungleichförmig.“2
Die ungleichförmige Bewegung wird weiterhin differenziert in die gleichförmig ungleichförmige Bewegung und die ungleichförmig ungleichförmige Bewegung. Sie werden folgendermaßen unterteilt:
„Die gleichförmig ungleichförmige Bewegung – wie man gemeinhin den Begriff bestimmt – ist etwas Dreifaches: Einmal ist sie gleichförmig ungleichförmig in Bezug auf das Subjekt allein, die nächste [Weise] in Bezug auf die Zeit allein, auf die letzte [Weise] aber in Bezug auf das Subjekt und die Zeit zugleich. Die gleichförmig ungleichförmige Bewegung nach dem Subjekt – wie man gemeinsam den Begriff bestimmt – tritt auf, wenn die Hälfte jedes möglichen Teils eines Subjekts so viel in der Geschwindigkeit von dem schnelleren Extremum von ihr übertroffen wird, wie es das Extremum, das langsamer bewegt wird, in der Geschwindigkeit übertrifft. Zum Beispiel die Bewegung einer Töpferscheibe. Und unter der Hälfte verstehe man den Punkt in der Mitte oder einen, an dem es vorstellbar ist, dort abgegrenzt zu werden. Eine gleichförmig ungleichförmige Bewegung nach der Zeit tritt hervor, wenn von jedem möglichen, gemäß der Zeit angenommenen Teil, in dem genau an irgendeinem Teil der Zeit eine mittlere Stufe ist, die in der Mitte eines solchen Teils ist, das verminderte Extremum so viel übertrifft, wie es von dem erhöhteren [Extremum] übertroffen wird. Zum Beispiel, wenn irgendein Bewegliches beginnt, von keiner Stufe aus bewegt zu werden, indem es stetig gleichförmig seine Bewegung über irgendeine Zeit hinweg erhöht, dann ist eine solche Bewegung gleichförmig ungleichförmig nach der Zeit. Eine gleichförmig ungleichförmige Bewegung nach der Zeit und nach dem Subjekt wird bestimmt, indem man die definitiones der gleichförmig ungleichförmigen Bewegung nach der Zeit und nach dem Subjekt vereinigt.“3
Und weiter:
„Eine ungleichförmig ungleichförmige Bewegung kann gemeinhin [so] aufgeteilt werden: Die eine [Weise] der ungleichförmig ungleichförmigen Bewegungen ist ungleichförmig ungleichförmig nach der Zeit, die andere [Weise] nach dem Subjekt und die letzte [Weise] nach der Zeit und dem Subjekt zugleich.“4
quaestio
In der nun folgenden quaestio zweifelt Alvarus Thomas an, dass die gleichförmig ungleichförmige Bewegung nach dem Subjekt ausreichend definiert wird. Dies wird verneint:
1. ratio:
„Wenn es irgendeine gleichförmig ungleichförmige Bewegung nach dem Subjekt gebe, wäre es besonders die Bewegung eines Rads, durch die es kreisförmig bewegt wird. Aber eine solche Bewegung ist nicht gleichförmig ungleichförmig nach dem Subjekt. Daher ist die Schlussfolgerung mit dem Obersatz offensichtlich. Und der Untersatz wird [so] argumentiert: Wenn eine solche Bewegung gleichförmig ungleichförmig ist, erfasse ich ein Rad, das gleichförmig ungleichförmig von keiner Stufe im Mittelpunkt bis zur achten [Stufe] im Umkreis bewegt wird. Und ich argumentiere so: Eine solche Bewegung ist durch dich gleichförmig ungleichförmig von keiner Stufe bis zur achten [Stufe]. Also steht ihre Geschwindigkeit mit einer mittleren Stufe in Verbindung, nämlich mit wie 4. Die mittlere Stufe wie 4 ist am mittleren Punkt eines solches Rads. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt. Die Schlussfolgerung ist offensichtlich nach der angenommenen opinio, die aussagt, dass eine gleichförmig ungleichförmige Bewegung mit einer Bewegung in Verbindung steht, die in der Mitte eines beweglichen Körpers ist.“5
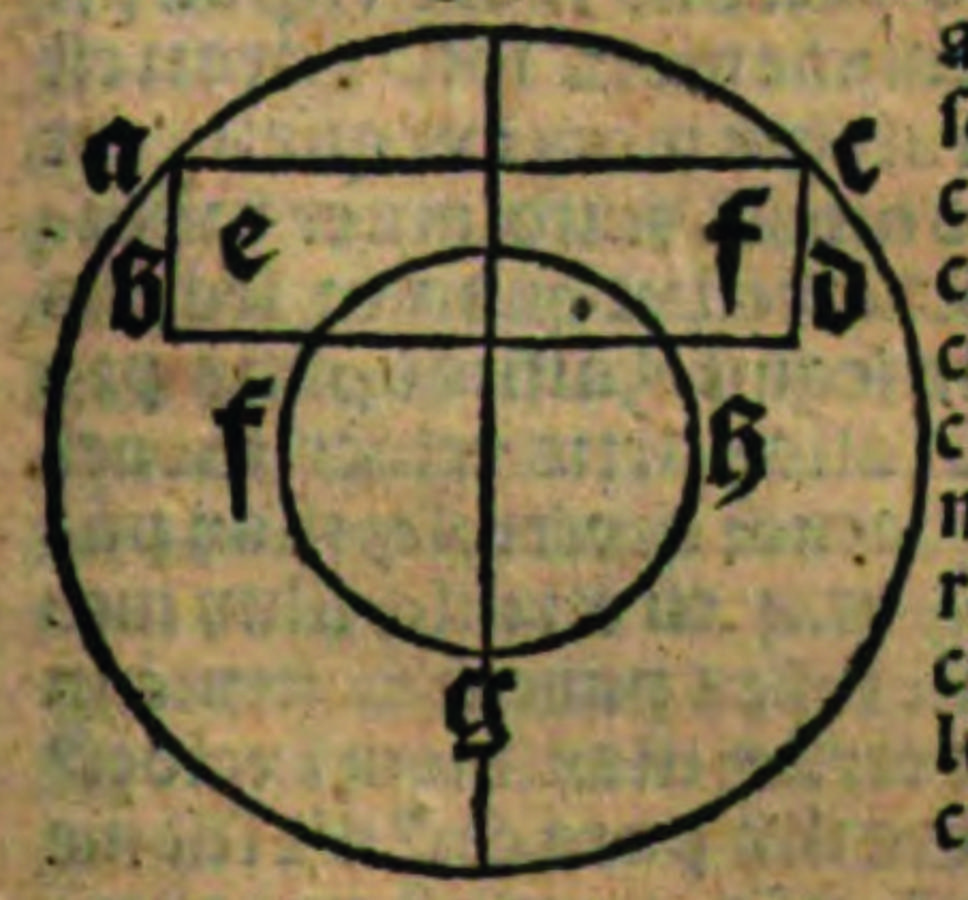
Abb. 1: Alvarus Thomas, Liber de triplici motu, S. 127.
Empfehlung von Alvarus Thomas:
„Stark und gut wirst du sprechen, indem du den Vordersatz verneinst und bei dem Beweis den Obersatz zugestehst und den Untersatz verneinst. Und wenn es bewiesen wird, lasse ich das Beispiel mit den [Gegebenheiten] zu, die dort angenommen wird, und ich gestehe den Vordersatz und die Schlussfolgerung zu. Und ich bestimme den Nachsatz in Bezug auf das Teilchen genau, über das gesagt wird, dass eine solche mittlere Stufe bei dem Punkt ist, der in der Mitte eines solchen Rads ist. Entweder du verstehst es von der Mitte der magnitudo jenes Rads her, die die Mitte ist in der Mitte zwischen dem Mittelpunkt und dem Umkreis eines solchen Rads, indem das Rad in zwei konzentrische Räder mit einer gleichen magnitudo geteilt wird, obwohl die Umkreise und die Umlaufbahnen ungleich sind, wie es offensichtlich ist in dem Bild. Und so verneine ich es. Oder du sagst es über den Punkt, der in der Mitte der Länge zwischen dem Mittelpunkt und dem Umkreis ist. Und so gestehe ich es gut zu, dass dort die mittlere Stufe ist, wie das Argument gut beweist.“6
conclusio:
„Daher sage ich, dass, obwohl in einer gleichförmig ungleichförmigen Qualität eine mittlere Stufe in der Mitte des Körpers in Bezug auf die magnitudo sein muss, es dennoch nicht bei einer gleichförmig ungleichförmigen Bewegung notwendig ist, dass die mittlere Stufe in der Mitte des Körpers in Bezug auf die magnitudo ist, sondern dass es notwendig ist, dass sie so in der Mitte des Körpers in Bezug auf die Länge ist, (indem die Länge von ihm von dem Punkt genommen wird, der nicht bewegt wird oder der am langsamsten bis zu dem Punkt bewegt wird, der am schnellsten bewegt wird). Gemäß dieser Weise schreitet die gleichförmig ungleichförmige Bewegung voran.“7
responsio zur 1. replica:
„Irgendein Teil des Rads wird nicht gleichförmig ungleichförmig bewegt. Also folgt daraus, dass das gesamte Rad nicht gleichförmig ungleichförmig bewegt wird.“8 Die Begründung lautet: „Es ist notwendig, dass in der gleichförmig ungleichförmigen Bewegung eines beliebigen Teils die mittlere Stufe – die dort ist, wo sie in der Mitte der Länge ist, wie gesagt worden ist – so viel die unterste [Stufe] übertrifft, wie sie von der obersten [Stufe] übertroffen wird (wie es offensichtlich ist aus der definitio).“9
2. replica:
„Aber dagegen [kann gesagt werden], dass beide Hälften des Quadrats ABCD schneller als wie 4 bewegt werden. Daher folgt, dass das gesamte Quadrat schneller als wie 4 bewegt wird. Die Schlussfolgerung ist offensichtlich: Die Geschwindigkeit des gesamten [Quadrats] wird aus den Teilgeschwindigkeiten erzeugt, und die denominatio der Geschwindigkeit aus den denominationes beider Hälften steht fest.“10
1. confirmatio: „Die schnellste Stufe einer beliebigen, gleichförmig ungleichförmigen Bewegung, in der der Punkt der Bewegung am schnellsten bewegt wird, übertrifft um so viel die mittlere Stufe, wie die mittlere Stufe die Stufe übertrifft, mit der der Punkt der Bewegung am langsamsten bewegt wird, wie diese opinio und die gemeinsame Schule zugesteht. Aber die Bewegung eines solchen Quadrats ABCD ist nicht von dieser Art. Daher ist eine solche Bewegung nicht gleichförmig ungleichförmig.“11
2. confirmatio: „Wenn die Bewegung eines solchen Rads gleichförmig ungleichförmig von keiner Stufe bis zur achten [Stufe] wäre, würde folgen, dass die adäquate Geschwindigkeit des Rads wie Vier wäre. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“12
Beweis von Thomas Bradwardine: „Aber jetzt beweise ich, dass [das Verhältnis] des gesamten Rads zu dem kleineren, zu ihm konzentrischen Kreis ein vierfaches Verhältnis ist, wie Bradwardine im Traktat über die Verhältnisse im vierten Kapitel zeigt: Zwischen zwei ungleichen Kreisen ist immer ein quadriertes Verhältnis in Bezug auf das Verhältnis, das zwischen den Diagonalen derselben Kreise ist. Daher ist das Verhältnis der Kreise das quadrierte Verhältnis der Diagonalen, wie es auch leicht gesehen werden kann in dem angenommenen Bild. Aber [das Verhältnis] der Diagonalen des gesamten Rads zu der Diagonalen des Kreises DEF ist ein doppeltes Verhältnis. Also ist [das Verhältnis] des gesamten Rads zu dem Kreis DEF ein vierfaches Verhältnis, nämlich ein doppelte [Verhältnis] zu einem doppelten [Verhältnis]. Was zu beweisen war.“13
„Und so ist aus dieser Ableitung offensichtlich, dass die gesamte Bewegung wie Fünf ist. Denn jene drei Viertel bestimmen [die Bewegung] wie Vier mit einer Hälfte, und das andere Viertel, das der kleinere Kreis ist, bestimmt [die Bewegung] wie eine Hälfte, (wenn sie wie Zwei ist). Daher ist die gesamte Bewegung wie Fünf und so ist sie nicht wie Vier. Was zu beweisen war.“14
2. ratio in Form einer sequala:
„Wenn diese definitio gültig wäre, würde folgen, dass die Bewegung des Himmels nicht gleichförmig ungleichförmig wäre nach dem Subjekt. Aber der Nachsatz ist das falsch und gegen diejenigen, die gemeinsam die [obrige] These vertreten.“15
confirmatio: „Wenn es irgendeine gleichförmig ungleichförmige Bewegung nach dem Subjekt gäbe, gäbe es höchstens eine lokale Bewegung, durch die ein Quadrat mit rarefactio bewegt wird, das heißt, dass sie gleichförmig von keiner Stufe bei dem ruhenden Extremum bis zur achten Stufe bei dem anderen Extremum ausgedünnt wird. Aber das ist sie nicht. Daher.“16

Abb. 3: Alvarus Thomas, Liber de triplici motu, S. 128.
argumentum in oppositum:
Hier führt Alvarus Thomas nur an, dass einige Philosophen an eine gleichförmig ungleichförmige Bewegung nach dem Subjekt glauben, ohne sie namentlich zu verzeichnen.
Es folgen vier conclusiones, zu den Ergebnissen der bisherigen Diskussion im Kapitel 3.2.1:
1. conclusio:
„Die gleichförmig ungleichförmige Bewegung nach dem Subjekt wird nicht gut auf diese Weise bestimmt: Die gleichförmig ungleichförmige Bewegung nach dem Subjekt ist eine [Bewegung], von der alle Teile, die unmittelbar der extensio sind, unmittelbar der intensio der Bewegung oder der Geschwindigkeit gemäß sind, so dass die vermindertste Stufe der Geschwindigkeit, die bei dem erhöhteren [Extremum] ist, die vermindertste [Stufe] ist, die nicht in dem verminderteren [Extremum] der zwei Teile ist, die zu sich unmittelbar sind.“17
2. conclusio:
„Die gleichförmig ungleichförmige Bewegung nach dem Subjekt ist auf diese Weise nicht gut bestimmt: Als gleichförmig ungleichförmige Bewegung nach dem Subjekt gilt, wenn ein Punkt jedes möglichen Teils des Subjekts, der in der Mitte ist – ich spreche von einem wahren oder einem vorstellbaren Punkt – um so viel in der Geschwindigkeit von einem Extremum jenes Teils übertroffen wird, das am schnellsten bewegt wird, wie er das Extremum übertrifft, das von demselben Teil am langsamsten bewegt wird oder nicht bewegt wird, (das sage ich wegen der Bewegung, die bei keiner Stufe begrenzt ist).“18
3. conclusio:
„So wird die gleichförmig ungleichförmige Bewegung nach dem Subjekt nicht gut bestimmt: Als gleichförmig ungleichförmige Bewegung nach dem Subjekt gilt, wenn die Hälfte jedes möglichen Teils des Subjekts oder der Punkt, der in der Mitte eines solchen Teils ist (in der Mitte – so sage ich – gemäß der Länge) um so viel in der Geschwindigkeit von dem Punkt oder dem Extremum, das am schnellsten bewegt wird, übertroffen wird, wie er den Punkt oder das Extremum, das am langsamsten bewegt wird, in der Geschwindigkeit übertrifft oder das Extremum [übertrifft], das nicht bewegt wird. (Das sage ich wegen der Bewegung, die bei keiner Stufe begrenzt wurde.)“19
4. conclusio:
„Eine gleichförmig ungleichförmige Bewegung nach dem Subjekt, wie mir jetzt erscheint, wird gut so bestimmt: Als gleichförmig ungleichförmige Bewegung nach dem Subjekt gilt, wenn ein beliebiger Punkt des Subjekts, der innen liegen kann und der sogar draußen liegen kann und am schnellsten bewegt wird, in dem Verhältnis schneller bewegt, in dem er weiter vom Mittelpunkt einer solchen Bewegung entfernt ist.“20
1. Korollar: „Ein beliebiger quantitativer Teil eines beliebigen [Körpers], der gleichförmig ungleichförmig nach dem Subjekt bewegt wird, kann gleichförmig ungleichförmig nach dem Subjekt bewegt werden.“21
2. Korollar: „Es ist nicht notwendig, dass eine gleichförmig ungleichförmige Bewegung nach dem Subjekt mit der Stufe der Bewegung in Verbindung steht, die in der Mitte der magnitudo eines solchen Körpers und auch nicht in der Mitte der Länge ist.“22
3. Korollar: „Eine gleichförmig ungleichförmige Bewegung nach dem Subjekt hat gemäß der mittleren Stufe zwischen der höchsten [Stufe] und der untersten [Stufe] oder keiner Stufe kommensurabel berechnet zu werden, wo auch immer eine solche Stufe ist. Das ist offensichtlich: Eine andere Weise, die Gesamtgeschwindigkeit einer gleichförmig ungleichförmigen Bewegung nach dem Subjekt zu ermitteln, scheint es nicht zu geben.“23
Daraus leitet sich die conclusio responsiva zu dieser quaestio ab:
conclusio responsiva:
„Jene definitio, die allgemeingültig über die gleichförmig ungleichförmige Bewegung nach dem Subjekt gegeben wird, ist nicht ausreichend ausgezeichnet worden, weil sie ja nicht gelten kann, wenn man sie von der Mitte der magnitudo versteht, und auch nicht [gelten kann], wenn man sie nicht von der Mitte der Länge her versteht, wie es im zweiten Korollar erklärt worden ist.“24
Zu den argumenta ante oppositum:
responsio von Alvarus Thomas zur 1. ratio:
Er stimmt im Grunde der conclusio responsiva zustimmt, nimmt aber in Einzelheiten davon Abstand: „Schließlich wird in dem ersten Argument nachgeforscht, ob es bei einer gleichförmig ungleichförmigen Bewegung nach dem Subjekt in der Mitte des Körpers gemäß der magnitudo oder gemäß der Länge eine mittlere Stufe sein muss. Ich sage, dass es von keiner jener Modi verlangt wird, in der Mitte des Körpers zu sein, wie es das zweite Korollar aussagt.“25
Die Begründung dafür lautet: „Dennoch wird nach dem Punkt gesucht, gemäß dem die Bewegung jenes Quadrats dort ermittelt werden muss. Ich sage, dass sie gemäß dem Punkt ermittelt werden muss, der in der mittleren Stufe zwischen der achten Stufe jenes Teils, mit der der Punkt bewegt wird, der am schnellsten bewegt wird, und der Stufe desselben Quadrats bewegt wird, mit der der Punkt bewegt wird, der am langsamsten bewegt wird, wo auch immer ein solcher Punkt sein wird. Denn über dessen Platz muss man sich nicht sorgen.“26
responsio von Alvarus Thomas zur 2. ratio:
„Zum zweiten Argument mit seiner confirmatio sage ich, dass sie für die conclusio responsiva sprechen, weil sie die definitio communis bekämpfen. Dennoch sage ich, dass die Bewegung des Himmels gleichförmig ungleichförmig ist, wie später gesagt werden wird. Denn ein beliebiger Punkt von ihr wird in dem Verhältnis schneller bewegt, in dem er weiter vom näheren Pol oder einem gleich nahen entfernt ist.“27
Dennoch sollte man laut Alvarus Thomas aber die opiniones der anderen Philosophen beachten.
1. opinio: „Die erste opinio ist von Wilhelm Heytesbery, der sagt, dass die Geschwindigkeit einer gleichförmig ungleichförmigen Bewegung nach dem Subjekt gemäß dem Punkt, der am schnellsten bewegt wird, ermittelt werden muss.“28
2. opinio, die besagt, „dass eine gleichförmig ungleichförmige Bewegung nach der Zeit gemäß der mittleren Stufe nach der Zeit ermittelt werden muss, das heißt nach der Stufe, nach der das Bewegliche in der Mitte einer solchen Zeit bewegt wird. Und die gleichförmig ungleichförmige Bewegung nach dem Subjekt muss nach der mittleren Stufe der gesamten gleichförmig ungleichförmigen latitudo ermittelt werden.29 Sie wird von Alvarus Thomas als communis opinio bezeichnet.
Dem fügt Alvarus Thomas folgende sechs Punkte hinzu:
1.:
„Dennoch muss es beachtet werden, wenn wir sagen, dass die Geschwindigkeit einer gleichförmig ungleichförmigen Bewegung gemäß der mittleren Stufe des Volumens ermittelt werden muss, zu sagen, dass ein solches Bewegliches, das gleichförmig ungleichförmig bewegt wird, genau so schnell bewegt wird, wie der Punkt bewegt wird, an dem die mittlere Stufe einer solchen latitudo ist. Und wenn gesagt wird, dass die Geschwindigkeit einer gleichförmig ungleichförmigen Bewegung nach der Zeit ermittelt werden muss gemäß der mittleren Stufe, die in der Mitte der Zeit ist, wollen wir sagen, dass das Bewegliche so schnell in genau der Zeit bewegt wird, wie es über die gesamte Zeit hinweg mit der Stufe bewegt werden würde, die es in der Mitte der Zeit hat.“30
2.:
„Weiterhin muss beachtet werden, dass die Geschwindigkeit einer Bewegung in Hinsicht auf die Wirkung gemäß dem Raum ermittelt werden muss, der durchquert wird, so dass gilt: Um wie viel der durchquerte Raum in der gleichen Zeit größer würde, um so viel wird die Bewegung schneller.“31
3.:
„Dennoch sage ich, dass die Geschwindigkeit der lokalen Bewegung nicht nach dem körperlichen Raum ermittelt werden muss und auch nicht nach dem Oberflächenraum, sondern dem Raum, der linear von einem feststehenden Punkt beschrieben wird. Denn wenn dann ein Pferd zwei ungleiche Balken gleich schnell ziehen würde, würde dennoch folgen, dass der größere [Balken] schneller bewegt werden würde, weil er einen größeren körperlich und oberflächlichen Raum als der kleinere [Balken] beschreibt. Das ist dennoch falsch. Sie werden gleich bewegt, wenn bei jedem der beiden der mittlere Punkt den gleichen Raum beschreibt.“32
4.:
„Und so muss auch über die gleichförmig ungleichförmige Kreisbewegung nach dem Subjekt gesagt werden, dass ihre Geschwindigkeit gemäß der Kreislinie ermittelt zu werden hat, die von dem Punkt beschrieben wird, an dem die mittlere Stufe der latitudo der gleichförmig ungleichförmigen Bewegung ist.“33
5.:
„Die Geschwindigkeit einer gleichförmig ungleichförmigen Bewegung nach der Zeit und nach dem Subjekt muss nach der Linie ermittelt werden, die von dem Punkt beschrieben wird, an dem die mittlere Stufe einer solchen latitudo ist.“34
6.:
„Und ebenso muss es über die ungleichförmig ungleichförmige Bewegung nach der Zeit gesagt werden, dass ihre Geschwindigkeit gemäß dem Raum ermittelt werden muss, der in einer solchen Zeit durchquert wird.“35
1. Korollar: „Aus diesen Dingen heraus wird schließlich angeführt, dass folgende Schlussfolgerung nicht gelten kann: Dieses Rad, das gleichförmig ungleichförmig nach dem Subjekt bewegt wird, beschreibt eine größere Linie als der Punkt, an dem die mittlere Stufe der gesamten latitudo der Bewegung ist. Daher wird es schneller bewegt als der Punkt. Der Vordersatz ist [erst] wahr, wenn ein Punkt, der auf dem Umkreis liegt oder der in der Peripherie des Rads, eine größere Linie beschreibt als der Punkt, an dem die mittlere Stufe der latitudo der Bewegung ist. Und jede der beiden Linien wird durch die Bewegung des Rads beschrieben.“36
2. Korollar: „Zweitens folgt, dass diese Schlussfolgerung nicht gilt: Dieses Rad wird gleichförmig ungleichförmig nach dem Subjekt bewegt. Und es wird die Kreislinie schneller durchschreiten, die der Linie gleicht, die von dem Punkt beschrieben wird, in dem die mittlere Stufe der latitudo ist, als ein solcher Punkt ist, an dem die mittlere Stufe der latitudo der Bewegung ist, seine Linie beschreibt. Also wird das Rad schneller bewegt als ein solcher Punkt.“37
3. Korollar: „Diese Schlussfolgerung gilt nicht: Der Balken wird einen größeren Raum durchschreiten als der [andere Balken] in derselben Zeit. Daher wird er in derselben Zeit schneller bewegt werden.“38
Kapitel 3.2.2
Kapitel 3.2.2 beschäftigt sich wie Kapitel 3.2.1 mit Fragen zur Geschwindigkeit einer ungleichförmigen lokalen Bewegung quoad subjectum.
quaestio:
„Es wird gefragt, nach welcher [Sache] – gleichsam in Hinsicht auf die Wirkung – die Geschwindigkeit einer ungleichförmigen Bewegung ermittelt zu werden hat, ob zum Beispiel gemäß einer von dem am schnellsten bewegten Punkt beschriebenen Linie oder in einer von einem Punkt beschriebenen Linie, in welchem die mittlere Stufe ist, oder gemäß einer reductio bis zur Einförmigkeit.“39
1. ratio:
„Und es wird zuerst argumentiert, dass sie nicht gemäß der ersten [Möglichkeit] ermittelt werden darf, wie es Heytesbury in seinem Traktat über die lokale Bewegung im ersten Kapitel meint, weil wenn [man das tun würde], mit dem gleichen Argument folgen würde, dass sie gemäß dem Punkt ermittelt werden müsse, der am langsamsten bewegt wird. Aber das ist falsch, weil er niemals gegeben werde. Daher.40 Und weiter: „Meistens ist kein Punkt, der sich sehr langsam bewegt, gegeben; und daher könnte keine Geschwindigkeit einer Bewegung bei einem solchen Punkt ermittelt werden.“41
replica:
„Aber dagegen kann man sagen, weil – wie weiter unten gesehen werden wird – irgendeine ungleichförmige Bewegung in Bezug auf ein Subjekt angeben werden kann, von der der Punkt, der stetig am schnellsten bewegt wird, nicht angegeben wird, wie es bei einem Mühlstein offensichtlich sein wird, der dünner wird. Daher kann sie auch nicht stetig gemäß einem solchen Punkt ermittelt werden. Und wenn ein solcher Punkt stetig bleibt, ist es dennoch nicht die Linie, die er genau beschreibt.“42
confirmatio: „Dann folgen würde, dass ein Rad, das gleichförmig ungleichförmig bewegt wird, ständig so schnell bewegt werden würde wie seine Hälfte, die schneller bewegt wird. Aber das ist falsch.“43
replica:
„Aber dagegen [kann gesagt werden], dass meistens kein extremer Punkt gegeben wird, wie dargelegt wurde, dass Gott in einem Rad alle extremen Punkte vergehen lässt. Ebenso wird beim Nominalisieren kein Extrempunkt gegeben. Denn er verneint, dass alle solche unteilbaren Sachen begrenzt sind, und er sich dem Abbild widersetzt. Daher kann nicht einmal die Geschwindigkeit einer ungleichförmigen Bewegung nach dem Subjekt gemäß der Linie, die von dem am schnellsten bewegten Punkt beschrieben wird, gemäß dem Weg der Nominalisten angenommen werden. Du wirst sagen, dass bei einem solchen Beispiel die Geschwindigkeit jener Bewegung gemäß der Linie ermittelt werden muss, die von einem vorgestellten, in der Peripherie liegenden Punkt beschrieben wird. Das heißt, dass das gesamte Rad eine so große Linie beschreibt und so schnell bewegt wird, wie schnell ein Punkt bewegt wird, der in der Peripherie eines solchen Rads wäre.“44
replica:
„Aber dagegen [kann so argumentiert werden:] Ich erfasse ein Rad, dass ungleichförmig nach dem Subjekt bewegt wird. Und wenn es beginne bewegt zu werden, beginne es durch die rarefactio so vergrößert zu werden, dass der Extrempunkt von ihm immer weiter vom Mittelpunkt entfernt ist. Daher ist am Anfang des gesamten Rads die Diagonale ein Fuß und am Ende zwei Fuß.“45 Und weiter heißt es: „Die Geschwindigkeit einer solchen Bewegung kann nicht ermittelt werden gemäß der Linie, die von dem am schnellsten bewegten Punkt beschrieben wird.“46 Und weiter: „Ein solcher Punkt beschreibt keine Linie. Das wird so bewiesen: [Der Punkt beschreibt] keine kreisförmige [Linie], wie es bekannt ist, wenn er nicht zu demselben Punkt zurückkehrt, von dem er abweicht, sondern zu dem Punkt, der um das Doppelte weiter vom Mittelpunkt entfernt ist. Und er beschreibt auch keine gerade Linie. Und es scheint nicht [so], dass er eine andere Linie beschreibt. Daher wird dort keine Linie angegeben, die von einem solchen Punkt gemäß dem beschrieben wird, gemäß dem die Geschwindigkeit des Rads bemessen werden könnte.“47
confirmatio: „Dadurch wird dieses Rad nicht so schnell bewegt, wie ein Extrempunkt von ihm am Anfang der Bewegung bewegt wird – wie bekannt ist – weil [der Punkt] über die gesamte Zeit eine größere Linie beschreibt, als wenn das Rad gemäß der magnitudo unverändert bliebe, und [zwar] auch nicht mit einer so großen Geschwindigkeit, wie er am Ende der Bewegung bewegt wird, und auch nicht zu dem mittleren Zeitpunkt der Bewegung. Dann würde es zusammenfallen mit einer anderen opinio, die [die Geschwindigkeit] gemäß der mittleren Stufe bemisst. Daher scheint sie nicht gemäß dem zu sein, gemäß dem die Geschwindigkeit einer solchen Bewegung ermittelt zu werden hat. Und so wird erachtet, dass nicht die ganze Geschwindigkeit einer ungleichförmigen Bewegung nach dem Subjekt gemäß der Geschwindigkeit des am schnellsten bewegten Punkts ermittelt zu werden hat.“48
2. ratio in Form einer sequela:
„Wenn das wahr wäre, würde diese conclusio folgen: Irgendein Bewegliches würde stetig gleichförmig bewegt werden, und dennoch würde ein beliebiger innen liegender Punkt stetig seine Bewegung erhöhen. Aber das scheint unmöglich.“49
replica in Form einer sequela:
„Dagegen [kann gesagt werden], dass unter gleichen Bedingungen folgen würde, dass irgendein Bewegliches stetig gleichförmig bewegt würde, und dennoch ein beliebiger, innen liegender Punkt seine Bewegung vermindern würde. Aber das erscheint unpassend.“50
replica in Form einer sequela:
„Dagegen [kann gesagt werden], dass dann folgen würde, dass von einem beliebigen verhältnismäßigen Teil irgendeines Beweglichen beim Fortschreiten in einer feststehenden Teilung irgendeine Geschwindigkeit weggenommen werde, so dass ein beliebiger [Teil] beim Fortschreiten in einer feststehenden Teilung mit einer kleineren Geschwindigkeit bewegt werde, als es vorher bewegt wurde. Und dennoch wird das gesamte Bewegliche stetig gleichförmig bewegt und gleich schnell wie vorher. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“51
3. ratio in Form einer sequela:
Sie richtet sich gegen den Satz der quaestio, dass die Gesamtgeschwindigkeit nicht nach der mittleren Stufe ermittelt werden solle. Es heißt: „Wenn das wahr wäre, würde folgen: Wenn ein Rad ungleichförmig nach dem Subjekt von keiner Stufe aus bis zu einer feststehenden Stufe ungleichförmig bewegt werden würde, so dass jener Teil, der vom Mittelpunkt bis zur Hälfte der Halbdiagonalen ist, von keiner Stufe bis zur vierten [Stufe] bewegt werde, und der restliche Teil bis zum Umkreis bewegt werde von der vierten [Stufe] bis zur zwölften [Stufe], dann würde ein solches Rad mit einer Geschwindigkeit wie sechs bewegt werden. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“52
replica:
„Aber dagegen [kann gesagt werden]: Wenn bei jeder gleichförmig ungleichförmigen Bewegung nach dem Subjekt die Geschwindigkeit gemäß der mittleren Stufe ermittelt werden müsse, daher entweder unter der mittleren Stufe die Stufe verstanden wird, die in der Mitte eines solchen Subjekts nach der magni tudo ist, oder die [Stufe], die in der Mitte nach der Länge ist, oder die [Stufe], die in der Mitte nach der magnitudo und der Länge zugleich. Aber keine von ihnen darf genannt werden. Daher muss die Geschwindigkeit einer gleichförmig ungleichförmigen Bewegung nach dem Subjekt nach der mittleren Stufe kommensurabel gemacht und ermittelt werden.“53
4. ratio in Form einer sequela:
Sie richtet sich ebenfalls gegen den Satz der quaestio, dass die Gesamtgeschwindigkeit nicht nach der mittleren Stufe ermittelt werden solle. Es heißt: „Wenn jener Teil wahr wäre, würde folgen, dass der Himmel nicht so schnell bewegt wird, wie die Äquinoktiallinie (und ich spreche vom ersten Beweglichen). Aber der Nachsatz ist falsch. Daher auch der Vordersatz. “54 Und weiter: „Die consequentia ist offensichtlich. Und die Falschheit des Nachsatzes wird ausgemalt: Wenn er nicht so schnell bewegt wird wie die Äquinoktiallinie, und die Äquinoktiallinie die Linie ist, die in der Mitte von ihm ist, wird also das Bewegliche, das gleichförmig ungleichförmig nach dem Subjekt bewegt wird, nicht so schnell bewegt wie der Punkt, der in der Mitte von ihm ist.“55
replica:
„Aber dagegen [kann gesagt werden]: Sie muss gemäß der Linie ermittelt werden, die entweder vom mittleren Punkt in einer konkaven Oberfläche beschrieben wird oder [vom mittleren Punkt] in einer konvexen Oberfläche [beschrieben wird]. Aber nichts davon darf gesagt werden. Daher.“56 Und weiter: „Der Punkt, der in Bezug auf eine konvexe Oberfläche in der Mitte ist, ist nicht einfacherweise in der Mitte, und auch nicht der Punkt, der in der konkaven Oberfläche [in der Mitte] ist. Daher. Ebenso wird ein solches Bewegliches nicht so schnell bewegt wie die konvexe Oberfläche und nicht so langsam wie die konkave Oberfläche. Also folgt, dass die Geschwindigkeit von ihm nicht gemäß dem Punkt ermittelt zu werden hat. Das bedeutet gemäß der Linie, die von einem Punkt beschrieben wird, der in der konvexen Oberfläche liegt und nicht auf der konkaven Oberfläche [liegt].“57 Abschließend heißt es: „Du wirst sagen, dass die Geschwindigkeit des ersten Beweglichen bemessen werden muss von dem Punkt, der in der Mitte zwischen der konvexen und der konkaven Oberfläche liegt, zwischen dem Pol und dem Punkt, der vom gesamten Kreis am schnellsten bewegt wird.“58
replica in Form einer sequela:
„Denn dann würde diese conclusio folgen: Wenn das erste Bewegliche gegen die konvexe Oberfläche verdichtet werden würde, die ruht, würde es stetig immer schneller bewegt werden. Und wenn es ausgedünnt werden würde gegen die konkave [Oberfläche], während die konvexe [Oberfläche] dazu noch ruht, würde das Bewegliche immer stetig langsamer bewegt werden. Aber der Nachsatz ist falsch. Denn dann würde folgen, [dass gilt]: Um wie viel auch immer ein Bewegliches größeres werden würde, umso viel langsamer würde es bewegt werden. Und m wie viel auch immer [ein Bewegliches] kleiner [werden würde], um so viel [wäre das Bewegliches] schneller. Das erscheint absurd.“59
replica in Form einer sequela:
„Denn dann würde folgen: Wenn alle Kreisbahnen, die dazwischen liegen, zerstört werden, und das erste Bewegliche auf einer ruhenden konvexen Oberfläche gegen die Achse ausgedünnt wird, bis aus der Kreislinie eine feste Kreisbahn wird, die nur eine einzige Oberfläche hat, dann wird das Bewegliche durch die Schaffung einer festen Kreisbahn bei weitem langsamer als vorher bewegt. Und es würde gleichförmig ungleichförmig nach dem Subjekt bewegt werden. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“60
confirmatio in Form einer sequela: „Wenn die opinio wahr wäre, würde folgen: Wenn irgendein Rad stetig gegen den Mittelpunkt verdichtet werden würde, während sich auch die konvexe Oberfläche bewegt, und der Beweger sich nicht mit größerer Anstrengung bewegt, würde das Rad dennoch stetig immer langsamer bewegt werden. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“61 Und schließlich: „Ebenso [gilt]: Diese Drehung ist so schnell wie vorher. Und diese Drehung ist der Kreisbeweger. Daher ist die Kreisbewegung so schnell wie vorher. Und folgerichtig wird das Rad dann nicht langsamer bewegt.“62
replica in Form einer sequela:
„Wenn diese Lösung gültig wäre, würde folgen, dass von demselben Verhältnis des Vermögens zu seinem Widerstand ungleiche Bewegungen entstehen und gleiche Drehungen. Das ist falsch.“63
replica:
„Denn nachdem das angegeben wurde, wird jetzt die Grundlage des gesamten Themas zerstört. Und mit ebensolcher Leichtigkeit würde jetzt ein dreister Physiker sagen, dass von einem doppelten Verhältnis und von einem vierfachen Verhältnis gleiche Geschwindigkeiten zu entstehen begannen. Und vieles ähnliche [könnte behauptet werden], was für den Kalkulator und den Philosophen absurd ist.“64 Dies würde laut Alvarus Thomas Folgendes implizieren: „Die magnitudo des Rads erhält sich aus einem Teil des Vermögens. Während auf die Weise derselbe Aufwand des Vermögens bestehen bleibt, wird das Rad langsamer bewegt und von einem kleineren Verhältnis [bewegt]. Vorher half die magnitudo des Rads dem Vermögen, die Linie zu beschreiben. So aber [gilt]: Wenn das Rad stetig kleiner wird, hilft es dem Vermögen nicht so wie vorher. “65 Und weiter mit einem Beispiel: „Denn es ist deutlich: Wenn zu der Oberfläche irgendeines Rads irgendetwas dem Rad Angrenzendes ohne Schwere von derselben species hinzugefügt wird, und Sokrates das gesamte [Rad] mit demselben Aufwand drehe, wird das gesamte Rad schneller bewegt, als vorher ein Teil von ihm bewegt wurde. Und dennoch bleibt das Vermögen gleich, und auch der Widerstand des Rads [bleibt gleich], aber das gesamte Verhältnis ist größer, weil dort dem Vermögen des Sokrates von der magnitudo des Rads geholfen wird.“66
replica:
„Die magnitudo erhält sich aus dem Teil des Widerstands, also nicht aus dem Teil des Vermögens, wobei sogar ganz und gar die gleiche gravitas bestehen bleibt. Der Vordersatz wird durch die Kreislinie bewiesen, die durch eine rarefactio vergrößert wird, bis sie eine feste Kreisbahn ist. Dann wird sie langsamer bewegt, als wenn sie kleiner war, wie es offensichtlich ist aus der zweiten replica des vierten Arguments. Du wirst sprechen, wie gesprochen werden muss: Weder die magnitudo noch die parvitas bei solchen [Sachen] erhält sich aus dem Teil des Vermögens, wie die replica ausreichend beweist; sondern der Abstand des Punktes vom Mittelpunkt – gemäß dessen Bewegung die Geschwindigkeit des gesamten Beweglichen ermittelt werden muss, nämlich des Punktes, der die mittlere Stufe der Bewegung der gesamten latitudo ist – erhält sich aus dem Teil des Vermögens.“67 Und weiter: „Denn – wenn die übrigen [Gegebenheiten] gleich bleiben – hilft es dem Vermögen, die Linie schneller zu beschreiben, als es sie beschreibt, wenn er vom Mittelpunkt zurückweicht. Und umgekehrt hilft es, sie langsamer zu beschreiben, wenn er näher an den Mittelpunkt herangeht, von dem die Bewegung entsteht. Und so sage ich: Wenn sich das Rad zum Umkreis hin ausdünnt, während der Umkreis sich bewegt, wird das gesamte Verhältnis größer, und wenn es auf die umgekehrte Weise verdichtet wird, wird das gesamte Verhältnis kleiner.“68
replica:
„Die Lösung reicht nicht aus bis hierher. Denn es folgt, dass aus ungleichen Verhältnissen gleiche Drehungen entstehen. Das ist unmöglich.“69
5. ratio:
Das fünfte Argument ist ebenfalls gegen den nachfolgeden Satz der quaestio gerichtet: „Irgendeine Bewegung ist gleichförmig ungleichförmig nach dem Subjekt. Und dennoch steht ihre Geschwindigkeit nicht mit der mittleren Stufe in Verbindung.“70
probatio ad exemplum: „Ich nehme an, dass eine rarefactio eine lokale ungleichförmige Bewegung nach dem Subjekt ist. Nachdem das angenommen wurde, lege ich dar, dass es zwei Fuß gebe gemäß jeder Dimension, nämlich A und B. Und ich will, dass A gleichförmig ausgedünnt werde, bis es um das Doppelte länger und um das Doppelte breiter gleichförmig werde. Und B werde gleichförmig ausgedünnt, bis es gleichförmig um das Anderthalbfache länger und um das Anderthalbfache breiter werde, so dass A am Ende ein Quadrat sei, dessen Seite doppelt zur Seite am Anfang der rarefactio sei. Und B sei ein anderes Quadrat, dessen Seite am Ende der rarefactio anderthalbfach zu seiner Seite am Anfang der rarefactio sei. Nachdem das dargelegt wurde, wird so argumentiert: Wenn die Bewegungen, durch die A bewegt wird, und auch [die Bewegungen], durch die B bewegt wird , gemessen werden müssen gemäß dem mittleren Punkt, folgt, dass A genau um das Doppelte schneller als B bewegt werden würde. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“71
6. ratio:
Die sechste ratio richtet sich „gegen den dritten Teil der Frage, dass nämlich die Geschwindigkeit einer lokalen ungleichförmigen Bewegung nach dem Subjekt gemäß der reductio bis zur Einförmigkeit ermittelt werden muss.“72: „Die Kreisbewegung bei einem Kreissubjekt kann nicht bis zur Einförmigkeit vermindert werden. Daher darf sie auch nicht gemäß der reductio bis zur Einförmigkeit ermittelt werden.“73
confirmatio: „Wenn die Kreisbewegung irgendeines Rads bis zur Einförmigkeit von keiner Stufe bis zur achten [Stufe] vermindert wird, wäre es entweder notwendig, durch das Vermindern von irgendeinem Teil irgendeine feststehende Geschwindigkeit zu erfassen und in den gleichen Teil zu legen, wie es bei der reductio einer gleichförmig ungleichförmigen Qualität geschieht, oder beim Erfassen [der Geschwindigkeit] von irgendeinem Teil und dem Verlegen [der Geschwindigkeit] in einen kleineren [Teil] oder [beim Erfassen der Geschwindigkeit] von einem kleineren [Teil] und dem Verlegen [der Geschwindigkeit] in einen größeren [Teil], [dann entscheide ich Folgendes]:“74 „Nicht das Dritte: Denn dann würde leicht beim Vermindern bis zur Einförmigkeit bewiesen werden, dass die Geschwindigkeit des Rads unendlich sei. Denn ein Stufe würde vom ersten verhältnismäßigen Teil erfasst werden, und so viel [würde auch] vom zweiten [Teil erfasst werden], und so viel [würde auch] vom dritten [Teil erfasst werden]. Und sie würde über das gesamte Rad hinweg gelegt werden. Und so gäbe es eine unendliche Geschwindigkeit. Nicht das Zweite: Dann würde folgen, dass die gesamte Geschwindigkeit kleiner wäre als Vier, wenn zum Beispiel die Geschwindigkeit des gesamte Rads unmittelbar von ihm aufgestellt werden würde, und [wenn sie] dort gleichförmig wie Vier wäre und danach durch das Erfassen der Hälfte der latitudo der Bewegung bis zur Gleichförmigkeit vermindert wird, nämlich um zwei Stufen, und durch das Verlegen von diesen [zwei Stufen] in der anderen Hälfte. Und so würde die gesamte Geschwindigkeit wie Zwei bleiben. Und das Erste darf nicht genannt werden: Denn nach der Teilung des Rads in zwei konzentrische Teile, von denen der eine der vierte Teil des gesamten Rads und der Restliche gegen den Umkreis drei Viertel sei, wie in dem vorhergehenden Kapitel in der zweiten confirmatio dargelegt wurde, nämlich in der letzten des ersten Arguments.“75
responsio:
„Ich antworte als anderer [Disputationsteilnehmer], dass de facto die Geschwindigkeit einer ungleichförmigen Bewegung nach den Subjekt niemals durch eine reductio bis zur Gleichförmigkeit bemessen werden darf. Sondern sie muss bemessen werden nach der denominatio der Teile, die sich nicht auf die magnitudo beziehen, sondern auf die Länge [beziehen]. Ich will sagen, dass nicht in dem Verhältnis, durch das der eine Teil größer als der andere ist, die sich in dem Verhältnis darin befindende Geschwindigkeit der Bewegung in Bezug auf die denominatio der gesamten Geschwindigkeit mehr ausmacht. Sondern ich will sagen, dass in dem Verhältnis, in dem [ein Körper] länger ist – während die übrigen [Gegebenheiten] gleich bleiben – in dem [Verhältnis] er mehr in Bezug auf die denominatio der gesamten [Geschwindigkeit] ausmacht, so dass das Rad genau so bewegt wird wie eine Linie, die vom Mittelpunkt des Rads bis zum Umkreis voranschreitet. Und wenn eine solche Linie von keiner Stufe bis zur achten [Stufe] bewegt wird, dann auch das gesamte Rad.“76
replica in Form einer sequela:
„Wenn eine solche Weise des Erkennens der Geschwindigkeit einer ungleichförmigen Bewegung nach dem Subjekt allgemein valide wäre, würde folgen, dass ein Teil des Rads angebbar wäre, das gleichförmig ungleichförmig bewegt wird, der nicht gleichförmig ungleichförmig bewegt werden würde. Vielmehr wäre die Stufe nicht angebbar, durch die er genau bewegt wird. Aber eine beliebige [Stufe wäre] ungenau [angebbar] innerhalb des gesamten [Subjekts]. Und der Nachsatz steht jeder opinio entgegen. Daher [ist es auch] das, woraus er folgt.“77
7. ratio als argumentum in oppositum:
„Das Gegenteil gibt dennoch die gemeinsame Schule an, die versichert, dass die Geschwindigkeit einer ungleichförmigen Bewegung nach dem Subjekt auf irgendeine jener Weisen ermittelt werden oder bemessen werden müsse.“78
Zur Beantwortung der quaestio sind nach Alvarus Thomas folgende drei Punkte zu beachten, die auch als propositiones gelten:
1Die definitio der gleichförmig ungleichförmigen Bewegung nach dem Subjekt.79
2Die definitio der ungleichförmig ungleichförmigen Bewegung nach dem Subjekt.80
3„dass bei der Kreisbewegung zwei [Sachen] beachtet werden müssen, nämlich die Drehung und die Kreisbewegung, obwohl nämlich die Kreisbewegung und die Drehung dasselbe sind. Dennoch hat die Geschwindigkeit der Drehung und die Geschwindigkeit der Kreisbewegung gemäß etwas Anderem bemessen zu werden. So ist auch die weiße Farbe und die Ähnlichkeit dasselbe. Und gemäß etwas Anderem haben die intensio der weißen Farbe und die intensio der Ähnlichkeit erkannt zu werden. Das kann leicht aus der Dialektik erfahren werden.“81
causa: „Denn die Geschwindigkeit der Kreisbewegung wird nach der Linie ermittelt, die von einem feststehenden Punkt beschrieben wird.“82 Und weiter: „Aber die Geschwindigkeit der Drehung hat nach dem Winkel ermittelt zu werden, der in einer so oder so großen Zeit um den Mittelpunkt herum beschrieben wird. Wenn daher in gleicher Zeit zwei Bewegliche, die gleich oder ungleich sind und kreisförmig bewegt werden, gleiche Winkel um dem Mittelpunkt beschreiben, gehen sie gleich kreisförmig [um den Mittelpunkt herum] oder umkreisen [ihn] gleich. Wenn sie aber in derselben Zeit ungleiche Winkel um den Mittelpunkt herum beschreiben würden, stellt als bekannt sich heraus, dass ihre Drehungen ungleich sind.“83 Alvarus Thomas bezeichnet dies als communis opinio, als deren Vertreter er Paulus Venetus ansieht.84
replica:
„Dennoch könnte leicht die Geschwindigkeit der Drehung nach der Geschwindigkeit der Bewegung irgendeines Punkts, der gleich vom Mittelpunkt entfernt ist, ermittelt werden. Das bedeutet zu sagen: Wenn bei den zwei Beweglichen – seien sie gleich oder ungleich – zwei Punkte, die gleich vom Mittelpunkt entfernt sind, kreisförmig gleich bewegt werden, kreisen solche Beweglichen gleich.“85 Und weiter: „Dennoch wirst du nicht glauben, dass [es gilt]: Um wie viel der Punkt näher am Mittelpunkt ist, um so viel schneller kreist er. Wie ein beliebiger [Punkt] gleich schnell kreist mit einem anderen [Punkt], solange die Bewegung des Körpers gleichförmig ungleichförmig nach dem Subjekt ist. Daher ist es offenbar zu sehen, dass die Abstände der Punkte sich in keiner Weise auf die Geschwindigkeit der Drehung beziehen, (ich spreche vom Abstand vom Mittelpunkt), obwohl es meistens in Bezug auf die Geschwindigkeit der Kreisbewegung [geschieht].“86
Es folgen zwölf conclusiones:
1. conclusio:
„Die Geschwindigkeit einer gleichförmig ungleichförmigen Bewegung nach dem Subjekt darf nicht nach der Geschwindigkeit des Punktes in Bezug auf die magnitudo ermittelt oder bemessen werden, der in der Mitte des Körpers liegt.“87
2. conclusio:
„Die Geschwindigkeit einer gleichförmig ungleichförmigen Bewegung nach dem Subjekt darf nicht nach der Geschwindigkeit des Punktes in Bezug auf die Länge ermittelt werden, der in der Mitte des Beweglichen ist.“88
3. conclusio:
„Die Geschwindigkeit einer gleichförmig ungleichförmigen Bewegung nach dem Subjekt muss nach der mittleren Stufe der gesamten latitudo einer solchen gleichförmig ungleichförmigen Bewegung bemessen werden, wo auch immer eine solche Stufe sein wird – sei es in der Mitte des Körpers in Bezug auf die magnitudo oder auch nicht. (Darum muss man sich nicht sorgen.)“89
4. conclusio:
„Die Geschwindigkeit einer ungleichförmig ungleichförmigen Bewegung nach dem Subjekt kann nach der denominatio der Teile in Bezug auf die Länge erkannt werden.“90
5. conclusio:
„Es ist wahrscheinlich, dass die Geschwindigkeit einer ungleichförmigen Bewegung nach dem Subjekt nach der höchsten Stufe ermittelt werden muss.“91 Hier folgt Alvarus Thomas der Vorstellung von Thomas Heytesbery.
6. conclusio:
„Der Abstand der Punkte vom Mittelpunkt, von dem eine ungleichförmige Bewegung nach dem Subjekt voranschreitet, erhält sich aus dem Teil des Vermögens und vermehrt das Verhältnis des Vermögens zum Widerstand. Das dient besonders demselben Vermögen, und umgekehrt die Nähe. Weder die magnitudo noch die parvitas schaffen irgendetwas.“92
Korollar: „Es steht nicht [fest], dass irgendein Rad, das von der virtus des Sokrates wie Vier bewegt wird, ausgedünnt wird und durch eine stetige Verlängerung der Punkte vom Mittelpunkt vergrößert wird, und dass es stetig von demselben Verhältnis bewegt wird, während die übrigen [Gegebenheiten] gleich bleiben.“93
7. conclusio:
„Die Nähe oder der Abstand der Punkte vom Mittelpunkt führt nichts zusammen in Bezug auf die Geschwindigkeit der Umdrehung oder der Drehung – das ist dasselbe – während die übrigen [Gegebenheiten] gleich bleiben.“94
1. Korollar: „Es muss niemals zugestanden werden, dass ungleiche Kreisbewegungen von gleichen Verhältnissen stammen oder gleiche Drehungen von ungleichen Verhältnissen, wie die Lösung des vierten Arguments zeigt.“95
2. Korollar: „Wenn auf dieselbe Achse unendliche Räder gestellt werden, die immer kleiner werden, so dass [das Verhältnis] der Diagonalen des ersten [Rads] zur Diagonalen des zweiten [Rads] ein doppeltes [Verhältnis] ist und auch das [Verhältnis] der [Diagonalen] des zweiten [Rads] zur Diagonalen des dritten [Rads] und folgerichtig so weiter, und Sokrates alle diese Räder bewegt, und die Achse in der Mitte liegt, [dann] wird dort irgendein Rad bis ins Unendliche langsam bewegt. Nichtsdestoweniger dreht sich dennoch ein beliebiges Rad so schnell wie das erste [Rad].“96
3. Korollar: „In dem vorher genannten Beispiel bewegt Sokrates nicht genau mit demselben Verhältnis das erste Rad und das zweite [Rad], sondern das erste [Rad] mit einem größeren [Verhältnis] als das zweite [Rad]. Denn der Abstand der mittleren Punkte dient dem Vermögen des Sokrates.“97
Einleitung zur 8. conclusio:
Zuerst werden der achten conclusio drei suppositiones vorangestellt:
1. suppositio: „Wenn es zwei Quantitäten gibt, die eine gleichförmig gleiche profunditas haben und gleichförmig gleich breit sind, eine [Seite] länger als die andere [Seite] ist, [gilt]: In welchem Verhältnis auch immer eine [Seite] länger ist, in demselben [Verhältnis] ist sie auch größer.“98
2. suppositio: „Wenn zwei ungleiche Quantitäten gleichförmig gleich tief und gleich lang sind, und eine breiter als die andere, [gilt]: In welchem Verhältnis auch immer die eine [Seite] breiter ist, in demselben [Verhältnis] ist sie größer.“99
3. suppositio: „Wenn es zwei Quantitäten gibt, die gleichförmig gleich lang und gleich breit sind, und eine [Seite] sei in irgendeinem Verhältnis tiefer als die andere [Seite], [dann] ist sie in demselben Verhältnis größer, in dem sie tiefer ist.“100
8. conclusio:
„Das Verhältnis vollendeter und ebenso gleichförmig gleich tiefer Quader ist das quadrierte Verhältnis der Seiten. Ich nenne einen Quader vollendet, von dem alle Seiten gleich und alle Winkel rechte [Winkel und] gleich sind. Verstehe dies dennoch nicht [derart], dass ich sagen möchte, dass alle Seiten gleich sein müssen hinsichtlich jeder Dimension, sondern nur hinsichtlich Breite und Länge!“101
1. Korollar: „Das Verhältnis zweier kubischen Körper oder einfach vollendeter Quader, die irgendwie angegeben sind, oder Würfel, deren Länge gleich der Breite und der Tiefe ist, ist das dreimal mit sich selbst multiplizierte Verhältnis der Seiten.“102
2. Korollar: „Wenn zwei quaderartige Würfel gegeben sind, deren Seiten sich in einem anderthalbfachen Verhältnis verhalten, ist das Verhältnis des größeren quaderartigen [Körpers] zum kleineren [quaderartigen Körper] Siebenundzwanzigachtel, das heißt 27 zu 8.“103
3. Korollar: „Wenn zwei kubische Quader gegeben sind, deren Seiten sich in einem dreifachen Verhältnis zueinander befinden, wird zwischen dem größeren [Quader] und dem kleineren [Quader] ein Siebenundzwanzigeintelverhältnis gefunden, das [zum Beispiel] ein Verhältnis von 27 zu Eins ist.“104
9. conclusio:
„Nach der opinio, die darlegt, dass die Geschwindigkeit der ungleichförmig ungleichförmigen Bewegung nach dem Subjekt gemäß der höchsten Stufe ermittelt werden muss, ist das Verhältnis der Bewegung zweier Kreisbahnen oder Kreislinien und gleichsam zweier Kreise, die in gleicher Zeit kreisen, so wie das Verhältnis der zwei Diagonalen, wenn die übrigen [Gegebenheiten] gleich bleiben.“105
10. conclusio:
„Das Verhältnis der Bewegungen zweier fester Sphären ist wie das Verhältnis der Diagonalen.“106 Dazu stellt Alvarus Thomas fest: „Aber in Bezug auf die andere opinio ist offensichtlich: Die Geschwindigkeit einer festen Sphäre muss in Hinsicht auf die andere [opinio] nach der Linie ermittelt werden, die von dem mittleren Punkt der Halbdiagonalen zwischen dem Mittelpunkt und dem Umkreis beschrieben wird und folgerichtig von dem Punkt, der von einem Viertel der Halbdiagonalen beschrieben wird. Aber in welchem Verhältnis auch immer eine Diagonale größer als eine andere [Diagonale] ist, in demselben Verhältnis ist das eine Viertel größer als das eine Viertel der anderen [Diagonalen]. Also in welchem Verhältnis auch immer die Diagonale der einen festen Kreisbahn nach dieser opinio größer sein wird als die Diagonale der anderen [Kreisbahn], in demselben Verhältnis wird der mittlere Punkt der Halbdiagonalen eine längere Strecke beschreiben. Und folgerichtig wird das Verhältnis der Bewegung wie das Verhältnis der Diagonalen sein.“107
11. conclusio:
„Das Verhältnis der Bewegungen von zwei ungleichen Sphären, die sich in derselben Zeit umkreisen, solange sie fest sind, ist ein durch 3 geteiltes [Verhältnis] in Bezug auf das Verhältnis der Sphären untereinander.“108
Korollar: „Wenn ein Sphäre um das Achtfache größer als eine andere [Sphäre] ist, wird sie genau um das Doppelte schneller als die andere [Sphäre] bewegt. Und wenn eine Spähre um das Siebenundzwanzigachtelfache größer als die andere [Sphäre] ist, wird sie um das Anderthalbfache schneller als die andere [Sphäre] bewegt.“109
12. conclusio als conclusio responsiva:
„So wie es wahrscheinlich ist, dass die Geschwindigkeit einer Bewegung, die die gegenwärtige Forschungsfrage betrifft, nach der Linie ermittelt werden muss, die von einem Punkt aus beschrieben wird, an dem die mittlere Stufe ist, oder gemäß der reductio bis zur Gleichförmigkeit der denominatio, so ist es wahrscheinlich, dass eine solche Bewegung in Bezug auf die Linie ermittelt werden muss, die von dem Punkt aus beschrieben wird, der am schnellsten bewegt wird – sei ein solcher Punkt, der am schnellsten bewegt wird, ein wahrer [Punkt] oder vorgestellter [Punkt].“110
Kommentare von Alvarus Thomas ad rationes ante oppositum:
Alvarus Thomas entscheidet sich nicht für eine der dargelegten Lösungen. Es heißt: „Wir halten jede der beiden opiniones. Es ist der Mühe wert, alle Argumente aufzulösen. Gleichwohl stehen jene [Argumente], die gegen die eine opinio sind, für die [jeweils] andere.“111
Zur 1. ratio:
„Die Geschwindigkeit einer ungleichförmigen Bewegung nach dem Subjekt muss gemäß dem am schnellsten bewegten Punkt ermittelt werden.“112
Zur 1. replica: „Und auf die replica antworte ich, dass, obwohl niemals ein wirklicher Punkt gegeben wird, der am schnellsten bewegt wird, dennoch ein vorstellbarer [Punkt] angegeben werden kann. Das reicht aus. Und auf ähnliche Weise kann eine wirkliche Linie nicht angegeben werden, aber eine vorstellbare [Linie], die er beschreibt. Und ich spreche im Vorschlag über eine wirkliche [Linie] oder eine vorstellbare [Linie], wie es dem Vorschlag nützt.“113
Zur 2. replica: „Und in Bezug auf die zweite replica, die darlegt, dass ein Rad stetig so ausgedünnt werde, dass die Punkte außerhalb stetig weiter vom Mittelpunkt entfernt sind, gestehe ich das Beispiel zu und verneine den Vordersatz. Und bei dem Beweis verneine ich, dass er keine Linie beschreibt. Und wenn es bewiesen wird, weil sie nicht gerade und nicht kreisförmig ist, gestehe ich den Vordersatz zu und ich verneine die Schlussfolgerung. Denn es gibt viele Linien, die weder gerade noch kreisförmig sind, wie es bei der Linie für den mittleren geraden Teil und für den mittleren kreisförmigen [Teil] offensichtlich ist. Dasselbe ist offensichtlich über die kreisende Linie und über den Faden, der zum Globus zurückgeführt wird. Und daher sage ich, dass eine solche Linie sich verhält, als ob sie in Bezug auf diese Weise kreisend oder gekrümmt ist.“114
Zur 2. confirmatio: „Zu der zweiten confirmatio sage ich kurz, dass ein solches Rad so schnell bewegt wird wie der Punkt, der sein Extremum ist und genau in der gesamten Zeit bewegt wird. Und wenn du fragen solltest, mit wem die Geschwindigkeit des Punktes in der gesamten Zeit genau in Verbindung steht, antworte ich, wie es mir gerade erscheint, dass sie mit der Geschwindigkeit in Verbindung steht, die ein solcher Punkt bei dem mittleren Zeitpunkt der gesamten Zeit hat.“115
Zur 2. ratio:
Alvarus Thomas verneint die sequela, „dass nämlich [fest] stehen wird, dass der Extrempunkt so schnell bewegt wird, wie er vorher in einem beliebigen verhältnismäßigen Teil bewegt wurde, der ohne Geschwindigkeit ist oder ruht.“116 Und weiter: „Aber ich sage, dass, wenn irgendein verhältnismäßiger Teil bis zu keiner Stufe der Geschwindigkeit gelangen würde, das gesamte Rad ruht. Ich bin mir nicht sicher, ob es aber geschehen könnte, dass am Ende des Arguments dargelegt wird, dass nämlich die Hälfte der Geschwindigkeit von einem beliebigen [Teil] für den verhältnismäßigen Teil nach einer feststehenden Teilung weggenommen wird, ohne dass irgendetwas von dem Punkt weggenommen wird, der auf dem Umkreis des Rads liegt. Nichtsdestoweniger scheint mir, dass es bei der gleichen ratio zugestanden werden muss, wie der Vordersatz, der angeführt wurde, zugestanden wird.“117
Zur 3. ratio:
Alvarus Thomas verweist auf die conclusiones dieses Kapitels.
Zur 4. ratio:
Alvarus Thomas verweist auf die 7. conclusio dieses Kapitels. Er betont im folgenden: „Denn der Abstand der Punkte oder die Nähe tragen nichts zur Umlaufgeschwindigkeit bei, weder vermehrt er das Verhältnis, noch vermindert er es, aber [dafür] ist er ein Hindernis des Umkreisens. Das ist in etwas die Schwere, die in dem Körper ist, der herumgeführt wird. Denn wenn es keine Schwere geben würde oder irgendein anderes Hindernis, würde ein großes Rad gleich schnell wie ein kleines [Rad] umkreist. Und wenn das umkreisende Vermögen ein natürliches [Vermögen] wäre, würde es auf der Stelle sofort umkreist werden.“118
Zur 5. ratio:
Alvarus Thomas verneint diesen Ansatz und die daraus gezogene consequentia, auch wenn er bei dem angeführten Beispiel die Argumente durchaus nachvollziehen kann.119
Zur 6. ratio:
Alvarus Thomas hält die angeführte replica für ausreichend. Und weiter: „Dazu sage ich, dass die Bewegung einer solchen kreisenden Linie nicht bis zur Gleichförmigkeit vermindert werden darf, wie es die replica annimmt, sondern der gesamte Rest der Linie erfasst werden muss, der über dem Punkt ist, an dem die mittlere Stufe der Bewegung ist, durch die das gesamte Rad bewegt wird. Und wenn es die Hälfte der gesamten Linie wäre, so schnell wird deswegen die Kreislinie bewegt, wie eine gerade Linie, die vom Mittelpunkt bis zu seinem Umkreis ist. Und daher hat die Geschwindigkeit der Kreislinie nach der Geschwindigkeit einer solchen geraden Linie bemessen zu werden.“120
Zum argumentum in oppositum:
„Das Argument für das Gegenteil gilt nicht mehr für die eine opinio als für eine andere [opinio].“121
Kapitel 3.2.3
Das vorletzte Kapitel des zweiten Traktats behandelt Berechnungen zur Geschwindigkeit von gleichförmig ungleichförmigen und ungleichförmig ungleichförmigen Bewegungen in Hinblick auf die Zeit.
quaestio:
Die quaestio lautet, „ob jede gleichförmig ungleichförmige Bewegung nach der Zeit nach der mittleren Stufe bemessen werden muss, und jede ungleichförmig ungleichförmige [Bewegung] nach der Zeit gemäß der reductio bis zur Gleichförmigkeit oder nach der Berechnung der denominatio [bemessen werden muss], durch die [die Berechnung] das Bewegliche bewegt zu werden bestimmt.“122
1. ratio:
„Und zuerst wird argumentiert, dass die Geschwindigkeit einer gleichförmig ungleichförmigen Bewegung nicht nach der mittleren Stufe von ihr bemessen werden darf.“123 Das versucht Alvarus Thomas im Folgenden zu widerlegen.
responsio in Form einer sequela:
„Denn es würde folgen, dass jedes [Bewegliche], das gleichförmig ungleichförmig in irgendeiner Zeit von keiner Stufe bis zu einer feststehenden Stufe bewegt wird, das heißt von keiner Stufe zur zwölften [Stufe], um das Doppelte langsamer als ein Bewegliches bewegt werden würde, das über dieselbe Zeit hinweg stetig mit der zwölften Stufe bewegt wird. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“124
replica in Form einer sequela:
„Aber dagegen [kann gesagt werden], dass dann folgen würde, dass jedes [Bewegliche], das sich gleichförmig von keiner Stufe bis zu einer feststehenden Stufe bewegt, um das Dreifache schneller in der zweiten Hälfte der Zeit als in der ersten [Hälfte] bewegt wird. Aber der Nachsatz ist falsch.“125
replica in Form einer sequela:
„Aber dagegen [kann gesagt werden]: Wenn die Lösung gültig wäre, würde folgen, dass das Bewegliche in der zweiten Hälfte der ersten Hälfte um das Dreifache schneller bewegt werden würde als in der ersten [Hälfte] derselben Hälfte [der Zeit]. Nach der Teilung der Hälfte in zwei [Hälften] würde es in einem durch 3 geteilten [Verhältnis] bewegt werden. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“126
confirmatio in Form einer sequela: „Wenn eine beliebige, gleichförmig ungleichförmige Bewegung nach der mittleren Stufe bemessen werden muss, würde folgen, dass die Bewegung von der feststehenden Stufe bis zu keiner Stufe, wie zum Beispiel die [eine Bewegung], durch die irgendein Bewegliches von einer vierten [Stufe] bis zu keiner Stufe bewegt wird, indem es seine Bewegung in einer Stunde vermindert, und die [andere] Bewegung, durch die irgendein Bewegliches gleichförmig ungleichförmig von keiner Stufe bis zur vierten [Stufe] in derselben Stunde, gleich sein würden. Aber das ist falsch. Daher [ist es auch] das, woraus er folgt.“127
replica in Form einer sequela:
„Aber dagegen [kann gesagt werden], dass dann folgen würde: Wenn eine Bewegung wie 4 oder irgendeine andere [Bewegung] gleichförmig bis zu ihrem Doppelten erhöht werde, und eine andere, ihr gleiche Bewegung in derselben Zeit bis zu keiner Stufe oder bis zum Stillstand vermindert werde, dann wird die [Bewegung], die vermindert wird, bis ins Unendliche schneller vermindert, als die andere [Bewegung], die erhöht wird, erhöht wird. Dennoch ist das falsch, wenn die eine [Bewegung] eine so große latitudo erwirbt, wie sie die andere [Bewegung] verliert.“128 Zu dem Argument führt er aus: „Du wirst sprechen, indem du das angeführte [Argument] gültig unterscheidest, dass sie entweder bis ins Unendliche schneller in derselben Zeit mit geometrischer Geschwindigkeit vermindert werde – und so wird es zugestanden – oder mit arithmetischer [Geschwindigkeit] – und so wird es verneint.“129
replica in Form einer sequela:
„Aber dagegen [kann gesagt werden]: Es wäre nicht möglich, dass die eine Bewegung in begrenzter Zeit gleichförmig so schnell geometrisch erhöht werden würde, wie die ihr gleiche Bewegung gleichförmig in derselben Zeit bis zu keiner Stufe vermindert werden würde. Aber der Nachsatz erscheint falsch (weil die eine Bewegung die gleiche latitudo verliert, wie sie die andere [Bewegung] erwirbt.) Daher [ist es auch] das, woraus er folgt.“130
2. confirmatio in Form einer sequela: „Denn wenn eine gleichförmig ungleichförmige Bewegung mit ihrer mittleren Stufe in Verbindung stehen würde, würde folgen: Wenn zwei gleiche, gleichförmig ungleichförmige Bewegungen in einer Stunde vermindert werden würden, die eine [Bewegung] um das Doppelte schneller als die andere [Bewegung]. Wenn jene [Bewegung], die langsamer vermindert wird, bis zum durch 2 Geteilten vermindert wurde, [dann] wäre die andere [Bewegung] bis zum durch 4 Geteilten vermindert worden und nicht bis zum Stillstand oder bis zu keiner Stufe. Aber der Nachsatz ist falsch, wie es dem Einsichtigen offensichtlich ist. Daher [ist es auch] das, woraus er folgt.“131
3. confirmatio in Form einer sequela: „Wenn eine gleichförmig ungleichförmige Bewegung mit der mittleren Stufe in Verbindung stehen würde, würde folgen: Wenn es zwei gleiche, gleichförmig ungleichförmige Bewegungen gäbe, die von derselbe Stufe beginnen und bei derselben [Stufe] enden oder bei keiner Stufe, [und wenn] die eine [Bewegung] von ihnen, nämlich A, um das Doppelte schneller stetig erhöht werden würde als die andere [Bewegung], nämlich B, und eine solche intensio bis ins Unendliche anndauern würde, [dann] wäre irgendwann die Bewegung A doppelt in Bezug auf B. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“132
4. confirmatio: „Wenn jede gleichförmig ungleichförmige Bewegung nach der mittleren Stufe bemessen zu werden hat, daher ist entweder in einer beliebigen solchen Bewegung die mittlere Stufe genau in einem durch 2 geteilten [Verhältnis] zu dem erhöhteren Extremum einer solchen Bewegung oder größer als ein durch 2 geteiltes [Verhältnis] oder kleiner. Nichts davon darf gesagt werden.“133 Und weiter: „Bei jeder gleichförmig ungleichförmigen Bewegung aber, die auf beiden Seiten von einer Stufe begrenzt wird, ist die mittlere Stufe größer als das durch 2 geteilte [Verhältnis] in Bezug auf das erhöhtere Extremum.“134
replica in Form einer sequela:
„Aber dagegen [kann gesagt werden], dass dann folgen würde, dass irgendwann die mittlere Stufe irgendeiner gleichförmig ungleichförmigen Bewegung, die auf beiden Seiten bei einer Stufe begrenzt ist, drei Viertel in Bezug auf die höchste Stufe sein würde, irgendwann zwei Drittel, irgendwann vier Fünftel und so bis ins Unendliche.“135 Und weiter: „Wenn du es nun zugestehst, wie es zugestanden werden muss, folgt, dass keine feststehende Regel gefunden werden kann und [auch] keine allgemeine [Regel], um es bei einer beliebigen gleichförmig ungleichförmigen Bewegung zu wissen, um wie viel mehr es durch die gesamte Bewegung in der erhöhteren Hälfte als in der verminderteren Hälfte durchquert wird. Das scheint ausreichend unpassend.“136
2. ratio:
„Wenn der erste Teil und der zweite [Teil] der quaestio wahr wären, würde folgen, dass irgendwelche zwei Bewegungen auf die Weise gleich [sind], und in gleicher Zeit gleiche latitudines nach und nach verlieren, so dass sie [auch] am Ende der Zeit gleich sein werden, und dennoch durch eine dieser Bewegungen ein größerer Raum stetig durchquert wird als durch die andere [Bewegung]. Das scheint unmöglich. Daher [ist es auch] das, woraus er folgt.“137
confirmatio: „Und es wird in der Annahme bestätigt: Denn ein verhältnismäßiger Teil nach einem vierfachen Verhältnis ist [wie] zwei Teile nach einem doppelten Verhältnis. Und folgerichtig sind zwei verhältnismäßige Teile nach einem vierfachen Verhältnis 4 [Teile] nach einem doppelten Verhältnis und folgerichtig so weiter, wenn man nach Zahlen vorangeht, die pariter par sind.“138
Und weiter: „Nachdem dies angenommen wurde, werde ich so argumentieren: In dem Beispiel verliert B am Ende des ersten verhältnismäßigen Teils nach einem vierfachen Verhältnis den ersten verhältnismäßigen Teil nach einem doppelten Verhältnis der zu verlierenden latitudo. Und dann verliert A zwei verhältnismäßige Teile nach einem doppelten Verhältnis der zu verlierenden latitudo. Dann wurden zwei verhältnismäßige Teile der Zeit nach einem doppelten Verhältnis überquert, wie es aus dem Angenommenen offensichtlich ist. Und die Bewegung A wird gleichförmig vermindert, wie es in dem Beispiel offensichtlich ist.“139
Und weiter: „Aber am Ende des zweiten verhältnismäßigen Teils der Zeit nach einem vierfachen Verhältnis verliert B zwei verhältnismäßige Teile der zu verlierenden latitudo nach einem doppelten Verhältnis und A 4 [Teile]. Wie jene zwei Teile nach einem vierfachen Verhältnis sind die vier verhältnismäßigen Teile nach einem doppelten Verhältnis. Daher wurde stetig bis zu dem Endzeitpunkt von A eine größere latitudo verloren als von B. Und so ist immer zu einem beliebigen, innerhalb [der Zeit] liegenden Zeitpunkt jener Stunde die Bewegung B schneller als die Bewegung A. Was zu beweisen war. “140
concessio:
„Es wird vielmehr zugestanden, dass die Bewegungen am Anfang gleich sind und auch am Ende gleich sind und sie die gleiche latitudo genau in derselben Zeit verloren haben, aber in der gesamten Zeit ist die eine [Bewegung] erhöhter als die andere [Bewegung], wie es das Argument schön beweist. “141
replica in Form einer sequela:
„Aber dagegen [kann gesagt werden]: Wenn die Lösung mit der Wahrheit übereinstimmend wäre, würde daraus eine solche conclusio gezogen werden, dass sich nämlich die zwei beliebige Bewegungen sich nur in einem doppelten Verhältnis zueinander verhalten und über dieselbe Zeit genau gleichförmig und gleich schnell vermindert werden würden. Und dennoch wird immer in der Zeit der Raum, der von der größeren [Bewegung] überquert wurde, mehr als das Doppelte in Bezug auf den Raum sein, der von der kleineren [Bewegung] durchquert wurde. Aber der Nachsatz ist falsch, wenn sie sich auf diese Weise in einem doppelten Verhältnis verhalten und immer gleich vermindert werden.“142 Und weiter: „Daher scheint es so, dass die [Bewegungen], die sich in einem doppelten Verhältnis befinden, stetig [gleich] bleiben. Und so ist der Raum, der von der größeren [Bewegung] durchquert wird, nicht mehr als das Doppelte in Bezug auf den Raum, der von der kleineren [Bewegung] durchquert wird. Und so ist der Nachsatz falsch. Und folgerichtig das, aus dem er folgt. Dennoch wird die sequela bewiesen und ich lege ein Beispiel dar: A und B seien Bewegungen, und A sei doppelt zu B. Und sie werden stetig gleich schnell und gleichförmig vermindert, indem A und B ganz und gar die gleiche latitudo über die gesamte Zeit hinweg verlieren.“143
3. ratio in Form einer sequela:
„Wenn eine ungleichförmig ungleichförmige Bewegung nach der reductio in Bezug auf die Gleichförmigkeit oder nach der denominatio ihrer intensio bemessen zu werden habe, würde die Schlussfolgerung folgen, dass es nämlich irgendeine ungleichförmige Bewegung geben könnte, die nicht bis zur Gleichförmigkeit vermindert werden könnte und deren intensio nicht feststehend angegeben werden könnte. Der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“144 Und weiter: „Und allgemein [betrachtet] ist zu beobachten, dass [es gilt]: In welchem Verhältnis aus immer sich ein Teil der Zeit in Bezug auf die gesamte Zeit befindet, in demselben [Verhältnis] verhält sich die Geschwindigkeit der Bewegung in jenem Teil zur Geschwindigkeit der gesamten Bewegung in der gesamten Zeit.“145
concessio:
„Du wirst ausdrucksstark sprechen, indem du als gültig zugestehst, dass keine bestimmte intensio einer solchen Bewegung und keine rationale reductio bis zur Gleichförmigkeit angegeben werden kann, so dass sich die intensio der Bewegung sich zur Bewegung irgendeines ihrer Teile in irgendeinem rationalen Verhältnis befindet. Das ist nicht unpassend und auch nicht gegen den Titel der quaestio. Der Titel der quaestio wird verstanden, so lange die Teile, in die solche Bewegungen gestellt werden, sich in einem rationalen Verhältnis befinden.“146
replica:
„Aber gegen [diese] Lösung wird so argumentiert: Denn es gibt irgendeine ungleichförmige Bewegung, deren Teile in Teilen der Zeit liegen, die ein rationales Verhältnis zur gesamten Zeit haben. Und dennoch kann eine solche Bewegung nicht bis zur Gleichförmigkeit vermindert werden, und es kann keine feststehende intensio gefunden werden. Daher gilt die Lösung nicht.“147
replica in Form einer sequela:
„Aber dagegen [kann gesagt werden], dass dann folgen würde: Wenn die Stunde in verhältnismäßige Teile nach einem dreifachen Verhältnis geteilt wird, und über den ersten [Teil] von ihnen hinweg irgendein Bewegliches mit einer irgendwiegroßen Geschwindigkeit bewegt werde, und über den zweiten [Teil] hinweg mit der doppelten Geschwindigkeit und über den dritten [Teil] hinweg mit der dreifachen [Geschwindigkeit] und so bis ins Unendliche [bewegt werde] wie in dem vorherigen Beispiel, [dann] würde ein solches Bewegliches in der gesamten Zeit genau mit der doppelter Geschwindigkeit in Bezug auf die Geschwindigkeit bewegt werden, mit der es im ersten verhältnismäßigen Teil der Stunde bewegt wird. Aber der Nachsatz ist falsch. Daher [ist es auch] das, woraus er folgt.“148
4. ratio:
„Es gibt irgendeine ungleichförmig ungleichförmige Bewegung, deren Gleichförmigkeit nicht angebbar ist und auch nicht die intensio der denominatio. Daher ist der Titel der Frage falsch.“149
replica:
„Aber dagegen [kann gesprochen werden], indem man das Beispiel ein wenig verändert. Ich will, dass A im ersten verhältnismäßigen der Stunde nach einem doppelten Verhältnis irgendwie schnell bewegt wird und im zweiten [Teil] um das Anderthalbfache schneller als im ersten [Teil], und im dritten [Teil] um das Vierdrittelfache schneller als im ersten [Teil], und im vierten [Teil] um das Fünfviertelfache schneller als im ersten [Teil] und folgerichtig so weiter beim Voranschreiten über alle species eines superpartikularen Verhältnisses hinweg, indem man immer auf den ersten Teil referiert.“150 Und weiter: „Nachdem das dargelegt wurde, wird so argumentiert: Eine solche Bewegung ist ungleichförmig ungleichförmig nach der Zeit und kann nicht bis zur Gleichförmigkeit vermindert werden, noch kann ihre feststehende intensio gefunden werden. Daher ist der Untersatz offensichtlich. Das Verfahren ist nämlich nicht ersichtlich, durch die die Bewegung bis zur Gleichförmigkeit vermindert werden könnte. Und wenn ein Gegner das verneint, gebe er das Verfahren an. Und im Zweifel wird es einem Kalkulatorphilosophen leicht fallen, es zu bekämpfen.“151
1. confirmatio: „Wenn irgendein Bewegliches im ersten verhältnismäßigen Teil dieser Stunde in irgendeinem Verhältnis irgendwie schnell bewegt wird, und im zweiten [Teil] um das Doppelte schneller und im dritten [Teil] um das Vierdrittelfache schneller als im ersten [Teil], und im vierten [Teil] um das Sechsfünftelfache schneller als im ersten [Teil], und im fünften [Teil] um das Neunachtelfache schneller, und im nachfolgenden [Teil] um das Dreizehnzwölftelfache schneller und so bis ins Unendliche, indem man interskalar durch die species eines superpartikularen Verhältnissesvoranschreitet, [und] indem man stetig ein [Verhältnis] mehrfach auslässt, dann ist eine solche Bewegung ungleichförmig ungleichförmig nach der Zeit. Und eine feststehende intensio kann nicht angegeben werden.“152
2. confirmatio: „Ich lege das Beispiel dar, dass im ersten verhältnismäßigen Teil irgendein Bewegliches irgendwie schnell bewegt werde und im zweiten [Teil] um das Anderthalbfache schneller als in ersten [Teil], und im dritten [Teil] um das Fünfdrittelfache schneller als im ersten [Teil], und im vierten [Teil] um das Vierdrittelfache schneller als im ersten [Teil], und im fünften [Teil] um das Siebenviertelfache schneller als im ersten [Teil], und im sechsten [Teil] um das Fünfviertelfache schneller als im ersten [Teil] und so folgerichtig weiter beim Voranschreiten über alle species eines superpartikularen Verhältnisses unterbrochen von species eines suprapartienten Verhältnisses. Dann wird ein solches Bewegliches ungleichförmig nach der Zeit bewegt und dennoch kann die Gleichförmigkeit der Bewegung nicht gefunden werden. Daher ist der Titel der quaestio falsch.“153
3. confirmatio: „Ich lege das Beispiel dar, dass das Bewegliche A in dem ersten verhältnismäßigen Teil irgendwie [schnell] bewegt wird, und im zweiten [Teil] um das Doppelte mehr, und im dritten [Teil] um das Anderthalbfache mehr als im ersten [Teil], und im vierten [Teil] um das Fünfdrittelfache mehr als im ersten [Teil], und im fünften [Teil] um das Fünfhalbefache mehr als im ersten [Teil], und im sechsten [Teil] um das Achtdrittelfache schneller als im ersten [Teil], und im siebenten [Teil] um das Dreifache schneller als im ersten [Teil] und so folgerichtig weiter, indem man zuerst fünf und dann weiterhin 5 andere erfasst und so bis ins Unendliche.“154 Und weiter: „Nachdem das dargelegt wurde, ist die Bewegung von ihnen ungleichförmig ungleichförmig, und [dennoch] kann ihre Geschwindigkeit nicht erfasst werden.“155
5. Argumentum in oppositum:
„Umgekehrt gilt dennoch die allgemeine opinio derer, die gemeinsam philosophieren, die in diesem Teil viel an scharfer Lebenskraft aussprüht. Außerdem wird durch eine beliebige solche ungleichförmige Bewegung in der gesamten Zeit genau irgendein Raum genau durchquert, und ein solcher Raum begann, in einer solchen Zeit mit irgendeiner gleichförmigen Geschwindigkeit durchquert zu werden. Daher ist diese gleichförmige Geschwindigkeit so groß, wie es die Geschwindigkeit der ungleichförmigen Bewegung ist, mit der der Raum in derselben Zeit genau durchquert wird.“156
Zur Beurteilung dieser quaestio folgen drei notabilia:
1. notabile:
Ungleichförmige Bewegungen unterscheiden sich in gleichförmig ungleichförmige und ungleichförmig ungleichförmige Bewegungen.157 Und weiter: „Aber die gleichförmig ungleichförmige Bewegung nach der Zeit ist bis dahin [auch] zweifach. Denn eine [Bewegung] ist gleichförmig ungleichförmig und begrenzt bei keiner Stufe beim anderen Extremum. Die andere [Bewegung] ist gleichförmig ungleichförmig und auf beiden Seiten bei einer Stufe begrenzt. Und über beide von diesen [Bewegungen] sagt man, dass sie mit ihrer mittleren Stufe in Verbindung stehen – das heißt, dass die Bewegung mit der Stufe [in Verbindung steht], die sie in der Mitte der Zeit hat. Denn um wie viel schneller ein Bewegliches bewegt wird, das gleichförmig ungleichförmig bewegt wird, wenn es sich mitten in der erhöhten Hälfte einer solchen Bewegung befindet, um soviel langsamer wird es bewegt, wenn es in der Mitte der verminderteren Hälfte ist, und so wird es gleich schnell bewegt, als ob es mit der mittleren Stufe bewegt werden würde.“158
Für eine solche mittlere Stufe stellt Alvarus Thomas propositiones auf:
1. propositio:
„Bei jeder gleichförmig ungleichförmigen latitudo, die bei einer Stufe beginnt und bei keiner Stufe begrenzt wird, ist die mittlere Stufe durch 2 geteilt in Bezug auf das erhöhtere Extremum. Wenn daher die latitudo von der achten [Stufe] beginnt und bei keiner [Stufe] begrenzt ist, ist die mittlere Stufe die vierte Stufe. Die vierte Stufe ist durch 2 geteilt in Bezug auf die achte [Stufe].“159 Alvarus Thomas verweist im Anschluss an den Beweis der propositio auf das erste Kapitel des Traktats zur lokalen Bewegung von Thomas Bradwardine, der diese propositio laut dem Autor auf eine andere Art und Weise beweist.
2. propositio:
„Die mittlere Stufe einer gleichförmig ungleichförmigen Bewegung, die auf beiden Seiten bei einer Stufe begrenzt ist, ist erhöhter als das durch 2 geteilte in Bezug auf das erhöhtere Extremum.“160
3. propositio:
„Die erhöhtere Hälfte einer beliebigen latitudo einer gleichförmig ungleichförmigen Bewegung, die bei keiner Stufe begrenzt ist, ist um das Dreifache erhöhter als die vermindertere Hälfte.“161
4. propositio:
„Jedes Vermögen, das sich gleichförmig ungleichförmig bewegt und eine latitudo hat, die bei keiner Stufe begrenzt ist, durchschreitet [einen Raum] um das Dreifache schneller in der Hälfte [der Zeit], in der es erhöhter bewegt wird, als in der Hälfte der Zeit, in der es verminderter bewegt wird. Wenn es zum Beispiel in der Hälfte, in der es verminderter bewegt wird, einen Fuß durchschreitet, durchschreitet es in der anderen [Hälfte] drei Fuß.“162
Korollar: „Wenn das Bewegliche A über eine Stunde hinweg gleichförmig ungleichförmig bis zu einer feststehenden Stufe bewegt wird, wobei es von keiner Stufe aus beginnt, und in der ersten Hälfte eine Meile durchschreitet, wird es in der zweiten Hälfte einen Raum von drei Meilen absolvieren. Und wenn es nach der umgekehrten Ordnung beginnen würde bewegt zu werden, nämlich von einer gegeben Stufe bis zu keiner Stufe, bleibt eine [Meile] zum Durchschreiten in der zweiten Hälfte der Zeit übrig, nachdem in der ersten Hälfte der Stunde drei Meilen absolviert wurden.“163
5. propositio:
„Wenn irgendein Bewegliches gleichförmig ungleichförmig von keiner Stufe bis zu einer feststehenden Stufe in irgendeiner Zeit bewegt werde, durchschreitet es genau einen durch 2 geteilten Raum in Bezug auf den Raum, der begonnen wurde, mit der erhöhteren Stufe durchquert zu werden, die über dieselbe Zeit andauerte.“164
6. propositio:
„Jedes Bewegliche, das gleichförmig ungleichförmig von einer feststehenden Stufe bis zu einer feststehenden Stufe in irgendeiner Zeit bewegt wird, durchschreitet einen größeren Raum als einen durch 2 geteilten [Raum] in derselben Zeit in Bezug auf den Raum, der begonnen wurde durchquert zu werden, wenn das erhöhtere Extremum der latitudo, das über dieselbe Zeit andauert, in der Mitte liegt.“165
7. propositio:
„Wenn irgendein Bewegliches gleichförmig ungleichförmig von einer feststehenden erhöhteren Stufe zu einer feststehenden verminderteren Stufe in einer Stunde bewegt werde, durchschreitet es in der ersten Hälfte der Zeit weniger als den dreifachen Raum in Bezug auf den Raum, der in der zweiten Hälfte der Stunde durchquert wird, in der es langsamer bewegt wird.“166
Es folgen zwei kurze quaestiones und die dazugehörigen responsiones:
1. quaestio:
Wie sei es bei jeder latitudo einer Bewegung zu erkennen, die auf beiden Seiten bei einer Stufe begrenzt ist, in welchen Verhältnis sich das erhöhtere Extremum zur mittleren Stufe derselben latitudo befindet, und in welchem Verhältnis mehr [Raum] durchquert wird, wenn die erhöhtere Hälfte einer solchen latitudo eher in der Mitte liegt, als wenn die verminderte Hälfte in der Mitte liegt?167
1. responsio:
„Ich antworte, dass bei diesem Thema keine feststehende und allgemeingültige Regel angegeben werden kann. Denn es gilt: Wie sich das erhöhtere Extremum und das verminderte [Extremum] zueinander in einem immer anderen Verhältnis verhalten, so verhält sich die mittlere Stufe zum erhöhteren Extremum einer solchen latitudo immer in einem anderen Verhältnis. Dennoch können besondere Regeln, die zu feststehenden species von Verhältnissen passen, ausgezeichnet werden.“168
2. quaestio und 2. responsio:
„Würde einer dennoch weiterhin fragen, wie man durch Faden und Maß die mittlere Stufe bei jeder latitudo ausfindig machen könnte, beantworte ich das durch diese Regel: Nur wenn die latitudo bei keiner Stufe begrenzt wird, dann teile man das erhöhtere Extremum in der Mitte und die eine Hälfte ist die mittlere Stufe. Wenn sie aber bei einer Stufe beginnt und bei einer Stufe beendet wird, dann ist die mittlere Stufe zwischen den Extrema das durch 2 geteilte Aggregatum aus dem erhöhteren Extremum und dem verminderteren [Extremum].“169
2. notabile:
„Zweitens muss bemerkt werden, dass die Geschwindigkeiten der Bewegungen – seien sie intensiv gleich oder ungleich – und [auch] wenn sie gleich sind, entweder zusammen in gleichen [Teilen] oder ungleichen Teilen der Zeit ausgedehnt sind.“170
1. Variante: „Wenn [die Geschwindigkeiten] aber gleich sind, beinhaltet es auch dasselbe [wie zuvor]: Entweder werden sie über gleiche Zeiten hinweg oder über ungleiche [Zeiten] hinweg ausgedehnt.“171
2. Variante: „Wenn [die Geschwindigkeiten] ungleich wären und in ungleichen Zeiten ausgedehnt werden würden, beinhaltet das etwas Zweifaches: Denn entweder wird die höhere Geschwindigkeit über eine größere Zeit oder über eine kleinere [Zeit] ausgedehnt.“172
exempla zur 1. und 2. Variante: „Ein Beispiel zur ersten [Möglichkeit]: Wenn eine Geschwindigkeit wie 4 in einer Stunde ausgedehnt wird, bedeutet das, dass ein Bewegliches wie 4 über eine Stunde hinweg bewegt werde und wie Zwei durch die Hälfte [einer Stunde]. Ein Beispiel zur zweiten [Möglichkeit]: Wenn irgendein Bewegliches mit einer Geschwindigkeit wie Vier über eine halbe Stunde hinweg bewegt werde und mit einer Geschwindigkeit wie Zwei über eine Stunde hinweg.“173
divisio der 2. Variante: „Ebenso [gilt das]: Wenn die höhere Geschwindigkeit in einer kleineren Zeit ausgedehnt werde, und die kleinere [Geschwindigkeit] in einer größeren [Zeit ausgedehnt werde], beinhaltet das etwas Dreifaches: Entweder übertrifft das Verhältnis der Zeiten das Verhältnis der Geschwindigkeiten, oder das Verhältnis der Geschwindigkeiten übertrifft das Verhältnis der Zeiten, oder das Verhältnis der Zeiten und das [Verhältnis] der Geschwindigkeiten sind gleich.“174
1. exemplum: „Ein Beispiel zur ersten [Möglichkeit]: Wenn irgendein Bewegliches in einer Stunde wie Zwei bewegt werde, und in einer Viertelstunde wie Vier, dann übertrifft das Verhältnis der Zeiten das Verhältnis der Geschwindigkeiten. Denn das Verhältnis der Zeiten ist vierfach, das [Verhältnis] der Geschwindigkeiten aber ist ein doppeltes [Verhältnis], wie es dem, der es anschaut, offensichtlich ist.“175
2. exemplum: „Ein Beispiel zur zweiten [Mögleichkeit]: Wenn ein Bewegliches wie Eins über eine Stunde bewegt werde und in einer halben [Stunde] wie 3, dann ist das Verhältnis der Zeiten ein doppeltes [Verhältnis], das [Verhältnis] der Geschwindigkeiten aber ein dreifaches [Verhältnis]. Daher übertrifft das Verhältnis der Geschwindigkeiten das Verhältnis der Zeiten.“176
3. exemplum: „Ein Beispiel zur dritten [Möglichkeit]: Wenn irgendein Bewegliches in einer Stunde wie Eins bewegt werde, und ein anderes [Bewegliches] in einer halben [Stunde] wie Zwei, [dann] steht fest, dass das Verhältnis der Zeiten dem Verhältnis der Geschwindigkeiten gleicht. Denn beide sind doppelt, das [Verhältnis] der Geschwindigkeiten und das [Verhältnis] der Zeiten.“177
Daher gelte:
1. propositio capitalis:
„Wenn die Geschwindigkeiten gleich sind und in gleichen Zeiten ausgedehnt [werden], absolvieren die Beweglichen, die mit eben diesen [Geschwindigkeiten] bewegt werden, gleiche Räume in denselben Zeiten, (alle übrigen [Gegebenheiten] werden abgeleitet), wie zum Beispiel bei einer rarefactio und einer Verdichtung des Raums und einer umgekehrten Bewegung, wie die conclusiones im sechsten [Buch] der Physik zeigen. Wenn aber gleiche Geschwindigkeiten über ungleiche Zeiten hinweg gleiten, dann durchschreitet ein Bewegliches in größerer Zeit einen größeren Raum als in kleinerer [Zeit, und zwar] in dem Verhältnis, in dem sich die größere Zeit sich zur kleineren [Zeit] verhält.“178
2. propositio:
„Wenn ungleiche Geschwindigkeiten über gleiche Zeiten hinweg zugleich ausgedehnt werden, dann durchschreitet das Bewegliche, das mit der höheren Geschwindigkeit bewegt wird, einen größeren Raum als das andere [Bewegliche, und zwar] in dem Verhältnis, in dem sich die höhere Geschwindigkeit zur niedrigeren [Geschwindigkeit] verhält.“179
3. propositio:
„Wenn ungleiche Geschwindigkeiten in gleichen Zeiten zugleich ausgedehnt werden, und die höhere Geschwindigkeit werde in einer größeren Zeit ausgedehnt und die niedrigere [Geschwindigkeit] in einer kleineren [Zeit], dann durchschreitet das Bewegliche, das in der größeren Zeit bewegt wird, einen größeren Raum, [und zwar] in dem Verhältnis, das aus dem [Verhältnis] von der größeren Zeit zur kleineren Zeit und dem [Verhältnis] der größeren Geschwindigkeit zur kleineren Geschwindigkeit zusammengesetzt ist.“180
1. Korollar: „Aus dieser propositio folgt zuerst: Wenn A über eine Stunde hinweg mit einer Geschwindgikeit wie 6 bewegt werde, und B über eine halbe Stunde hinweg mit einer Geschwindigkeit wie 4, wird der Raum, der von A durchquert wird, dreifach in Bezug auf den Raum sein, der von B durchquert wird.“181
2. Korollar: „Es folgt zweitens: Wenn das Bewegliche A über eine Stunde hinweg mit einer Geschwindigkeit wie 6 bewegt werde, und B über zwei Drittel einer Stunde hinweg mit einer Geschwindigkeit wie 4, durchschreitet A einen größeren Raum als B, [und zwar] in einem kleineren Verhältnis als in dem vorigen Beispiel.“182
4. propositio:
„Wenn eine höhere Geschwindigkeit in einer kleineren Zeit zugleich mit einer niedrigeren [Geschwindigkeit] in einer größeren [Zeit] ausgedehnt wird, und das Verhältnis der höheren Geschwindigkeit zu niedrigeren Geschwindigkeit gleich dem Verhältnis der größeren Zeit zur kleineren Zeit ist, dann durchschreiten die Beweglichen gleiche Räume.“183
Korollar: „Wenn das Bewegliche A über eine Stunde hinweg mit einer Geschwindigkeit wie 4 bewegt werde, und B über zwei Drittel einer Stunde mit einer Geschwindigkeit wie Sechs, durchschreiten B und A gleiche Räume.“184
5. propositio:
„Wenn eine höhere Geschwindigkeit in einer kleineren Zeit ausgedehnt wird, und eine niedrigere Geschwindigkeit in einer größeren Zeit [ausgedehnt wird], und das Verhältnis der Geschwindigkeit das Verhältnis der Zeit übertrifft, dann beschreibt ein Bewegliches, das in einer kleineren Zeit bewegt wird, einen größeren Raum als das Bewegliche, das in der größeren Zeit bewegt wird, [und zwar] in dem Verhältnis, durch das das Verhältnis der Geschwindigkeiten das Verhältnis der Zeiten übertrifft.“185
Korollar: „Aus dieser propositio folgt: Wenn das Bewegliche A über eine Stunde hinweg mit einer Geschwindigkeit wie 2 bewegt werde, und das Bewegliche B über eine halbe Stunde mit einer Geschwindigkeit wie 6, [dann] durchschreitet das Bewegliche B einen um das Anderthalbfache größeren Raum als A. Wie zum Beispiel wenn A zwei Fuß durchschreite, dann durchschreitet B drei Fuß.“186
6. propositio:
„Wo auch immer eine höhere Geschwindigkeit an die Seite einer kleineren Zeit tritt, [oder] eine niedrigere [Geschwindigkeit] zu einer größeren [Zeit tritt], und das Verhältnis der Geschwindigkeiten dem Verhältnis der Zeiten unterlegener und kleiner ist, dann beschreibt das Bewegliche, das mit einer höheren Geschwindigkeit bewegt wird, in einer kleineren Zeit eine kleinere magnitudo als das Bewegliche, das in größerer Zeit in dem Verhältnis bewegt wird, durch das das Verhältnis der Zeit zu dem Verhältnis der Geschwindigkeiten getragen wird.“187 Im folgenden Beweis wird auf das 1. Korollar der vierten conclusio des Kapitels 2.4 verwiesen, und es heißt: „Wann immer zwei ungleiche Zahlen zwei Verhältnisse zu einer dritten [Zahl] bilden, dann ist das kleinere [Verhältnis] von ihnen um das Verhältnis kleiner als das größere [Verhältnis], um das das größere Verhältnis das kleinere [Verhältnis] übertrifft. Das heißt, durch das das Verhältnis der größeren Zahl zur dritten [Zahl] das Verhältnis der kleineren Zahl zur dritten [Zahl] übertrifft. Denn das Verhältnis der größeren [Zahl] zu derselben dritten [Zahl] ist zusammengesetzt aus dem Verhältnis von ihr zur kleineren Zahl und dem [Verhältnis] der kleineren Zahl zu derselben dritten [Zahl].“188
Korollar: „Wenn ein Pferd A sich mit einer Geschwindigkeit wie 4 in einer Stunde genau bewegt, und das Pferd B mit einer Geschwindigkeit wie 6 in einer halben Stunde bewegt, und das Pferd B 6 Meilen in der halben Stunde überbrücke, ist es notwendig, dass das Pferd A in einer Stunde zu dem Extremum von 8 Meilen gelangt.“189
3. notabile:
„Es ist das eine, die latitudo einer Bewegung gleichförmig zu erhöhen oder gleichförmig zu vermindern, es ist aber etwas anderes, dass sich ein Bewegliches gleichförmig bewegt.“190
Und weiter: „Wenn daher die latitudo einer Bewegung gleichförmig von keiner Stufe oder von einer Stufe bis zu einer feststehenden Stufe erhöht wird, wird das Bewegliche gleichförmig ungleichförmig bewegt. Und wenn ebenso irgendeine Bewegung von einer Stufe bis zu keiner Stufe oder einer feststehenden Stufe vermindert wird, dann wird das Bewegliche gleichförmig ungleichförmig bewegt. Denn wenn die latitudo der Bewegung erworben oder verloren wird und gleichförmig ungleichförmig gemäß den Teilen der Zeit ausgedehnt wird, so dass die mittlere Stufe irgendeines Teils der Bewegung um so viel von der höchsten [Stufe] übertroffen wird, wie sie die unterste oder keine Stufe übertrifft, daher wird beim bestimmten Argumentieren ausgelassen, dass jede solche Bewegung, die so gleichförmig erworben wird oder verloren geht, gleichförmig ungleichförmig ist.“191
Empfehlung von Alvarus Thomas:
„Wende darüber hinaus an, dass eine latitudo einer Bewegung dreifach erworben werden kann – wie es in Bezug auf unseren Vorschlag ausreicht – oder auch verloren gehen [kann].“192
1. modus :„Auf die erste Weise kann die latitudo einer Bewegung stetig gleichförmig erworben werden oder verloren gehen, wie zum Beispiel, wenn ein Bewegliches in gleichen Teilzeiten gleiche Stufen der Geschwindigkeit erwirbt oder verliert.“193
2. modus:„Zweitens kann die latitudo einer Bewegung stetig immer schneller erworben werden oder verloren gehen, wie zum Beispiel wenn ein Bewegliches in einem beliebigen folgenden Teil der Zeit stetig eine größere latitudo der Bewegung verliert, als es sie in dem gleichen, vorhergehenden [Teil der Zeit verliert].“194
3. modus: „Auf die dritte Weise kann eine latitudo einer Bewegung oder die Geschwindigkeit stetig immer langsamer verloren gehen oder erworben werden, wie zum Beispiel wenn ein Bewegliches stetig in einem beliebigen folgenden Teil der Zeit eine kleinere latitudo der Bewegung verliert, als in dem gleichen [Teil der Zeit], der vorhergeht.“195
Dieser Aufteilung folgen sechs propositiones:
1. propositio:
„Wenn irgendeine Bewegung stetig gleichförmig von einer feststehenden Stufe bis zu einer feststehenden Stufe oder bis zu keiner Stufe erhöht werden würde oder vermindert werden würde, [dann] steht ihre Geschwindigkeit mit der mittleren Stufe in einer Verbindung.“196
2. propositio:
„Jede Bewegung, die stetig immer schneller erhöht wird, steht in Bezug auf die Geschwindigkeit mit der verminderteren Stufe in Verbindung als der mittleren Stufe zwischen dem Extremum ihrer intensio am Anfang der Bewegung und zwischen dem Extremum ihrer intensio am Ende ihrer Bewegung.“197
confirmatio: „Denn A und B sind am Anfang gleiche Bewegungen. Und in der gesamten Zeit müssen sie gleiche latitudines erwerben. Und an einem beliebigen, innen liegenden Zeitpunkt wurde zu A mehr von der zu erwerbenden latitudo erworben als zu B. Daher ist die Bewegung A stetig größer als B.“198
3. propositio:
„Jede Bewegung, die immer schneller in Bezug auf die Überquerung des Raums verloren geht, steht mit einer erhöhteren Stufe als der mittleren Stufe in Verbindung. Das bedeutet, dass ein solches Bewegliches, das durch die Bewegung bewegt wird, genau in der Zeit einen größeren Raum durchquert, als wenn es in der Zeit mit der mittleren Stufe zwischen den Extrema jener Bewegung stetig gleichförmig bewegt werden würde.“199 Dies entspricht nach Alvarus Thomas der 52. conclusio von Richard Swineshead.
1. Korollar: „Wenn das Bewegliche A in einer Stunde bewegt werde, indem es bei der achten [Stufe] beginnt und stetig gleichförmig seine Bewegung bis zur vierten [Stufe] vermindert, und das Bewegliche B werde auch in der Stunde bewegt, indem es seine Bewegung von der achten [Stufe] bis zur vierten [Stufe] immer schneller vermindert, und A 6 Fuß durchquere, [dann] wird B mehr als sechs Fuß durchqueren.“200 Der Beweis verweist auf den Beweis der vorangehenden 3. propositio.
2. Korollar: „Wenn A von der achten [Stufe] bis zur vierten [Stufe] gleichförmig bewegt zu werden anfinge, und B in derselben Zeit bewegt werde, indem es bei der sechzehnten [Stufe] beginne und bis zur zwölften [Stufe] eine latitudo von 4 Stufen immer schneller verliere, dann wird B stetig mehr als um das Doppelte schneller als A bewegt werden und stetig mehr als den doppelten Raum in Bezug zu dem Raum durchqueren, der in derselben Zeit von A durchquert wurde.“201
3. Korollar: „Wenn [A] wie auch B in der Stunde bis zu ihrer durch 2 geteilten [Stufe] vermindert werden würden, A in der Stunde stetig gleichförmig vier Stufen verliert und B stetig immer schneller 8 [Stufen verliert], folgt daraus, dass B mehr als den doppelten Raum in der Stunde durchqueren wird als A.“202
4. propositio:
„Jede Bewegung, die in Bezug auf Überquerung eines Raums immer langsamer erhöht wird, steht mit einer erhöhteren Stufe als der mittleren [Stufe] in Verbindung.“203 Diese popositio entspricht der 55. conclusio von Richard Swineshead.
5. propositio:
„Jede Bewegung, die immer langsamer verloren geht, steht mit einer verminderteren Stufe als der mittleren [Stufe] in Verbindung.“204 Alvarus Thomas verweist bei dieser propositio auf die 53. conclusio von Richard Swineshead.
Korollar: „Wenn das Bewegliche A gleichförmig ungleichförmig von der achten [Stufe] bis zur vierten [Stufe] bewegt werde, indem es stetig gleichförmig in einer Stunde eine latitudo wie 4 verliert, und das Bewegliche B in derselben Stunde von der achten [Stufe] bis zur vierten [Stufe] bewegt werde, indem es stetig auch eine latitudo wie 4 immer langsamer verliert, [dann gilt]: Wenn A 6 Fuß durchquert, so wird B weniger durchqueren werden.“205
6. propositio:
„Jede latitudo einer Bewegung, die ganz und gar auf ähnliche Weise verloren geht und erworben wird, steht ganz und gar mit einer Stufe in Verbindung. Ich will sagen, wenn es irgendeine Bewegung gebe, die um des Beispiels willen von keiner Stufe beginne und bis zur achten [Stufe] in einer Stunde genau gleichförmig erhöht werden würde, und eine andere oder dieselbe [Bewegung] in einer Stunde gleichförmig so von der achten [Stufe] bis zu keiner Stufe vermindert werden würde, wie sie erhöht wurde, [dann] steht eine solche Bewegung mit derselben Stufe in Verbindung.“206 Diese propostio entspricht der 56. conclusio von Richard Swineshead.
4. notabile:
„Die Geschwindigkeiten der Bewegungen können auf zweifache Weise erforscht werden, nämlich aus der Bemessung der Räume, die durchquert wurden, das bedeutet von der Wirkung her und von dem Späteren, das wir in dem gegenwärtigen Traktat nachforschen, aber auf die andere Weise aus der Bemessung und der Verhältnismäßigkeit der Verhältnisse, von denen die Geschwindigkeiten stammen.“207
Daher sollen laut Alvarus Thomas einige propositiones eingeführt werden:
1. propositio:
„Wenn eine beliebige Geschwindigkeit gegeben ist, und jedes mögliche Verhältnis vorgeschlagen wurde, [dann] kann durch einen fähigen Kopf mit einer gewissen Kunstfertigkeit untersucht werden, ob die gegebene Geschwindigkeit von dem vorgeschlagenen Verhältnis, einem kleineren [Verhältnis] oder einem größeren [Verhältnis] herstammt.“208
2. propositio:
„Wenn man zwei ungleiche Vermögen erfasst, die sich gegen denselben Widerstand bewegen, und ein Verhältnis zwischen den Vermögen verortet, und auch das Verhältnis verortet, in dem das größere Vermögen sich gegen den Widerstand schneller bewegt, als das kleinere [Vermögen] sich gegen denselben [Widerstand] bewegt, findet man mit einer gewissen Kunstfertigkeit heraus, wie viel das Verhältnis des größeren Vermögens zum Widerstand ist, und auch [wie viel] das [Verhältnis] des kleineren Vermögens zu demselben Widerstand [ist].“209
3. propositio:
„Wenn ein beliebiges Vermögen gegeben ist, das sich gegen zwei ungleiche Widerstände bewegt, zwischen den Widerständen ein bekanntes Verhältnis ist, und es bekannt ist, in welchem Verhältnis das gegebene Vermögen sich gegen den kleineren [Widerstand] schneller als gegen den größeren [Widerstand] bewegt, [dann] wird es erlaubt sein, mit mathematischem Aufwand die Verhältnisse des Vermögens zu beiden Widerständen herauszufinden, in welcher Weise sie nämlich existieren. Wenn Sokrates zum Beispiel in irgendeiner Zeit den Stein A von sich wirft oder in derselben oder einer gleichen [Zeit] den kleineren Stein B, und zwischen den Steinen ein bekanntes Verhältnis ist, um des Arguments willen ein doppeltes [Verhältnis], und Sokrates die Steine mit derselben virtus bewege, und es bekannt sei, dass Sokrates den Stein B um das Dreifache schneller als den Stein A bewege, haben wir um des Beispiels willen jetzt vor, mit der Fähigkeit der mathematischen Kunstfertigkeit herauszufinden, welches das Verhältnis ist, mit dem Sokrates den Stein B bewegt, und welches es sei, mit dem er den Stein A bewegt, ob sie nämlich beide doppelt sind, ob dreifach oder in irgendeinem anderen [Verhältnis]. Denn das ist nicht bekannt.“210
1. Korollar: „Wenn Sokrates den Stein B über einen so großen Raum bewegt, wie es die Diagonale des Quadrats ist, und den Stein A über einen so großen Raum, wie es die Seite desselben Quadrats ist, dann ist das Verhältnis von Sokrates zu dem Stein A, das heißt, mit dem er den Stein A bewegt, mehr als ein doppeltes [Verhältnis] in Bezug auf ein doppeltes Verhältnis. Und das Verhältnis, mit dem Sokrates den Stein B bewegt, ist mehr als das Dreifache in Bezug auf ein doppeltes [Verhältnis].“211
2. Korollar: „Das Verhältnis von Sokrates ist zu B mehr als ein achtfaches [Verhältnis]. Denn ein achtfaches [Verhältnis] ist ein dreifaches [Verhältnis] in Bezug auf ein doppeltes [Verhältnis], wie es offensichtlich ist aus der achten conclusio des sechsten Kapitels des zweiten Teils. Und das [Verhältnis] von Sokrates zu B ist größer als ein dreifaches [Verhältnis] in Bezug auf ein doppeltes [Verhältnis], wie bewiesen worden ist.“212
4. propositio:
„Wenn eine beliebige Geschwindigkeit angegeben wurde, und ein beliebiges Verhältnis ausgezeichnet wurde, ist es der Mühe wert, mit einem arithmetischen Apparat herauszufinden, ob das Verhältnis, durch das die Geschwindigkeit entsteht, kommensurabel zu dem ausgezeichneten Verhältnis ist, oder ob es nicht [der Mühe wert ist, das herauszufinden].“213
Es folgen zwölf conclusiones:
1. conclusio:
„Wenn irgendein Körper oder eine latitudo in verhältnismäßige Teile nach einem beliebigen Verhältnis aufgeteilt wurde, verhält sich der ganze Körper oder die latitudo zu dem Rest vom ersten verhältnismäßigen Teil in dem Verhältnis, durch das er oder die latitudo geteilt wird.“214
2. conclusio:
„Wenn irgendeine Zeit in verhältnismäßige Teile nach einem beliebigen Verhältnis aufgeteilt wird, und es irgendein Bewegliches gebe, das mit einer irgendwie großen Geschwindigkeit im ersten verhältnismäßigen Teil bewegt werde, und im zweiten [Teil] mit einer um das Doppelte größeren [Geschwindigkeit] als im ersten [Teil], und im dritten [Teil] mit einer um das Dreifache größeren [Geschwindigkeit] als im ersten [Teil], und im vierten [Teil] mit einer um das Vierfache größeren [Geschwindigkeit] und so weiter, indem man über alle species eines vielfachen Verhältnisses aufsteigt, [dann] verhält sich eine solche Geschwindigkeit der gesamten Zeit und aller ihrer verhältnismäßigen Teile zu der Geschwindigkeit des ersten verhältnismäßigen Teils in dem Verhältnis, in dem sich die gesamte Zeit, die so nach einer Ordnung geteilt ist, zum ersten verhältnismäßigen Teil verhält.“215
3. conclusio:
„Wenn eine Stunde oder irgendeine beliebige Zeit nach dem Verhältnis F, wenn du es wolltest, geteilt wird, und im ersten verhältnismäßigen Teil eines solchen Verhältnisses irgendein Bewegliches genau mit einer feststehenden Geschwindigkeit bewegt werde, und ein anderes Bewegliches oder dasselbe in der gesamten Stunde oder Zeit mit derselben Geschwindigkeit bewegt werde, dann [gelte]: In welchem Verhältnis auch immer sich die Zeit zum ersten verhältnismäßigen [Teil] verhalten wird, in dem Verhältnis wird sich der Raum, der in der gesamten Zeit absolviert oder durchquert wurde, zu dem Raum verhalten, der im ersten verhältnismäßigen Teil durchquert wurde. “216
4. conclusio:
„Wenn eine Stunde nach einem beliebigen Verhältnis, wie du es wolltest, in verhältnismäßige Teile geteilt wird, und im ersten der verhältnismäßigen Teile irgendein Bewegliches mit einer irgendwie großen Geschwindigkeit bewegt werde, und es im zweiten [Teil] mit einer Geschwindigkeit, die um das Doppelte größer ist als im ersten [Teil bewegt werde], und es im dritten [Teil] mit einer [Geschwindigkeit bewegt werde], die um das Dreifache größer als im ersten [Teil] ist, und so weiter, dann wird sich in dem Beispiel die gesamte Geschwindigkeit zur Geschwindigkeit des ersten verhältnismäßigen Teils in dem Verhältnis befinden, in dem sich die gesamte Zeit zu dem ersten verhältnismäßigen Teil von ihr befindet. Und der Raum, der genau in der gesamten Zeit durchquert wurde, wird sich zu dem Raum, der im ersten verhältnismäßigen Teil absolviert wurde, in einem verdoppelten Verhältnis verhalten.“217
Am Ende dieses Abschnitts formuliert Alvarus Thomas diese propositio verkürzt erneut so: „[Das Verhältnis] der Geschwindigkeit der gesamten Stunde zu der Geschwindigkeit des ersten verhältnismäßigen Teils ist das Verhältnis F. Und [das Verhältnis] der Zeit der gesamten Stunde, die größer ist, zu der Zeit des ersten verhältnismäßigen Teils ist auch das Verhältnis F. Also ist [das Verhältnis] des Raums, der in der gesamten Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde, das Verhältnis, das aus dem verdoppelten Verhältnis F zusammengesetzt ist. Und folgerichtig ist [das Verhältnis] des Raums, der in der gesamten Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde, ein doppeltes Verhältnis in Bezug auf das Verhältnis der Geschwindigkeiten, das F ist.“218
1. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem vielfachen Verhältnis geteilt wurde – sei es ein doppeltes, dreifaches, vierfaches oder ein beliebiges anderes vielfaches [Verhältnis] – und [wenn] im ersten verhältnismäßigen Teil irgendein Bewegliches irgendwie schnell bewegt werde, und im zweiten [Teil] es mit einer Geschwindigkeit [bewegt werde], die um das Doppelte größer als im ersten [Teil] ist, und im dritten [Teil] mit einer um das Dreifache größeren [Geschwindigkeit] als im ersten [Teil bewegt werde], wie es das Beispiel des vorhergehenden Theorems zeigt, [dann] wird [das Verhältnis] der gesamten Geschwindigkeit zu der Geschwindigkeit des ersten verhältnismäßigen Teils ein doppeltes Verhältnis sein, wenn die Teilung nach einem doppelten Verhältnis erfolgt wäre, und [es wird] ein anderthalbfaches [Verhältnis sein], wenn [sie] nach einem dreifachen [Verhältnis erfolgt wäre], und [es wird] ein vierdrittelfaches [Verhältnis sein], wenn [sie] nach einem vierfachen [Verhältnis erfolgt wäre] und so bis ins Unendliche, indem man reihenartig über die species eines superpartikularen Verhältnisses und eines vielfachen [Verhältnisses] vorangeht.“219
2. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem sechsfachen Verhältnis geteilt werden, und im ersten [Teil] von ihnen irgendein Bewegliches mit irgendeiner Geschwindigkeit bewegt werde, und im zweiten [Teil] mit einer um das Doppelte größeren [Geschwindigkeit], und im dritten [Teil] mit einer um das Dreifache [größeren Geschwindigkeit] – dies wurde öfter wiederholt – dann ist [das Verhältnis] der gesamten Geschwindigkeit zur Geschwindigkeit des ersten verhältnismäßigen Teils ein sechsfünftelfaches Verhältnis. Und das [Verhältnis] des Raums, der in der gesamten Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde, ist ein sechsunddreißigfünfundzwanzigfaches Verhältnis.“220
3. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem achtfachen Verhältnis aufgeteilt wird, und in denselben [Teilen] irgendein Bewegliches bewegt werde – so wie es mehrmals wiederholt wurde – [dann] ist [das Verhältnis] der gesamten Geschwindigkeit zur Geschwindigkeit des ersten verhältnismäßigen Teils ein achtsiebentelfaches Verhältnis. Und [das Verhältnis] des Raums, der in der gesamten Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde, wird ein doppeltes Verhältnis in Bezug auf ein achtsiebentelfaches [Verhältnis] sein, das heißt ein vierundsechzigneunundvierzigstelfaches [Verhältnis], wie es von 9 und ein Siebentel zu 7 und 64 zu 49 besteht.“221
5. conclusio:
„Wenn man eine Stunde in verhältnismäßige Teile nach einem superpartikularen Verhältnis teilt – einem anderthalbfachen, einem fünfviertelfachen oder einem beliebigen anderen superpartikularen [Verhältnis] – und die Geschwindigkeit auf die verhältnismäßigen Teile verteilt wird, so dass im ersten [Teil] von ihnen ein Bewegliches irgendwie schnell bewegt werde, und im zweiten [Teil] um das Doppelte schneller [bewegt werde], und im dritten [Teil] um das Dreifache schneller als im ersten [Teil bewegt werde] und so weiter in dem Beispiel, das öfter wiederholt wurde, dann verhält sich die gesamte Geschwindigkeit zu der Geschwindigkeit des ersten verhältnismäßigen Teils in einem dreifachen Verhältnis, wenn die Stunde nach einem anderthalbfachen Verhältnis geteilt werden würde. Wenn sie aber nach einem vierdrittelfachen Verhältnis geteilt werden würde, [dann verhält sie sich] in einem vierfachen [Verhältnis]. Wenn sie nach einem fünfviertelfachen Verhältnis [geteilt werden würde], [dann verhält sie sich] in einem fünffachen Verhältnis, und so [geht es] weiter, wenn man reihenartig über die species eines superpatikularen Verhältnisses und eines vielfachen [Verhältnisses] aufwärts schreitet. Und die Räume, die in der gesamten Zeit durchquert werden, verhalten sich zu den Räumen des ersten verhältnismäßigen Teils in einem verdoppelten Verhältnis. (Ich sage verdoppelt in Bezug auf ein dreifaches [Verhältnis] oder doppelt in Bezug auf ein dreifaches [Verhältnis], wenn die Teilung nach einem anderthalbfachen [Verhältnis] geschehen wäre, [oder ich sage] vierfach, wenn die Teilung nach einem vierdrittelfachen Verhältnis geschehen wäre, und folgerichtig so weiter).“222
1. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem beliebigen superpartikularen Verhältnis geteilt wurde, und die Geschwindigkeit wurde verteilt, wie in dem Beispiel der zweiten conclusio dargelegt wird, nämlich so, dass das Bewegliche irgendwie schnell im ersten verhältnismäßigen Teil bewegt werde, und [es] im zweiten [Teil] um das Doppelte schneller [bewegt werde], und [es] im dritten [Teil] um das Dreifache schneller als im ersten [Teil bewegt werde], und [es] im vierten [Teil] um das Vierfache schneller als im ersten [Teil bewegt werde] und so weiter, dann wird die gesamte Geschwindigkeit gleich der Geschwindigkeit des dritten verhältnismäßigen Teils sein, wenn die Teilung nach einem anderthalbfachen Verhältnis geschehen wäre. Und wenn die Teilung nach einem vierdrittelfachen [Verhältnis] gemacht wäre, wird die gesamte Geschwindigkeit gleich der Geschwindigkeit des vierten verhältnismäßigen Teils. Und wenn die Teilung nach einem fünfviertelfachen Verhältnis geschehen wäre, wird sie gleich der Geschwindigkeit des fünften verhältnismäßigen Teils sein und so weiter, wenn man vorwärts geht durch die species eines superpartikularen Verhältnisses und durch die verhältnismäßigen Teile.“223
2. Korollar: „Wenn die Stunde in verhältnismäßige Teile nach einem anderthalbfachen Verhältnis geteilt wurde, und [wenn] das Bewegliche A im ersten Teil irgendwie schnell bewegt werde, und [es] im zweiten Teil um das Doppelte schneller [bewegt werde], und [es] im dritten [Teil] um das Dreifache schneller als im ersten [Teil bewegt werde] und so weiter, so dass es im ersten verhältnismäßigen Teil einen Fuß durchquert, durchquert es in der gesamten Stunde neun [Fuß].“224
3. Korollar: „Wenn eine Stunde oder irgendeine Zeit nach einem beliebigen superpartikularen Verhältnis geteilt wurde, wie es im ersten Korollar vorgeschlagen worden ist, ist [das Verhältnis] des Raums, der in der gesamten Zeit durchquert wurde, zu dem Raum, der im ersten Teil durchquert wurde, ein doppeltes Verhältnis in Bezug auf das Verhältnis, das die Geschwindigkeit des dritten Teils zu der Geschwindigkeit des ersten Teils hat, wenn die Teilung nach einem anderthalbfachen Verhältnis geschehen wäre. Wenn es aber nach einem vierdrittelfachen Verhältnis geschehe, [dann wäre es] ein doppeltes [Verhältnis] in Bezug auf das Verhältnis der Geschwindigkeit des vierten Teils zu der Geschwindigkeit des ersten [Teils]. Wenn es in einem fünfviertelfachen Verhältnis [geschehe, dann wäre es] ein doppeltes [Verhältnis] in Bezug auf das Verhältnis der Geschwindigkeit des fünften Teils zur Geschwindigkeit des ersten [Teils] und so folgerichtig weiter.“225
4. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach irgendeinem beliebigen superpartikularen Verhältnis geteilt wurde, und irgendein Bewegliches im ersten [Teil] bewegt werde und so weiter, wie es dargelegt wurde, ist [das Verhältnis] des Raums, der in der gesamten Stunde durchquert wurde, neunfach in Bezug auf den Raum, der im ersten verhältnismäßigen Teil durchquert wurde, wenn die Teilung nach einem anderthalbfachen Verhältnis geschehen wäre. Wenn [sie] aber nach einem vierdrittelfachen Verhältnis [geschehen wäre], ist es sechzehnfach. Wenn aber nach einem fünfviertelfachen Verhältnis, ist es fünfundzwanzigfach. Daher durchquert er im ersten Teil einen Fuß und in der gesamten Stunde fünfundzwanzig Fuß und so weiter.“226
6. conclusio:
„Wenn die Stunde nach einem beliebigen Verhältnis geteilt wurde, und [es gelte], in welchem Verhältnis sich die zwei Teile unmittelbar zueinander verhielten, in demselben oder einem größeren Verhältnis würde sich die Geschwindigkeit des kleineren Teils zur Geschwindigkeit des größeren Teils verhalten, [und] die gesamte Geschwindigkeit unendlich ist, [dann] wird auch der Raum, der durchquert wurde, nach der gleichen ratio auch unendlich sein.“227
1. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem doppelten Verhältnis geteilt werde, so dass ein Bewegliches irgendwie schnell im ersten Teil bewegt werde, und [es] im zweiten [Teil] um das Doppelte schneller als im ersten [Teil bewegt werde], und [es] im dritten [Teil] um das Doppelte schneller als im zweiten [Teil bewegt werde], und [es] im vierten [Teil] um das Doppelte schneller als im dritten [Teil bewegt werde], [dann] wird der Raum, der durchquert wurde, unendlich sein.“228
2. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem vierdrittelfachen Verhältnis geteilt werde, und im ersten verhältnismäßigen Teil das Bewegliche A mit irgendeiner Geschwindigkeit bewegt werde, und [A] im zweiten um das Anderthalbfache schneller als im ersten [Teil bewegt werde], und [A] im dritten [Teil] um das Anderthalbfache schneller als im zweiten [Teil bewegt werde], und [A] im vierten [Teil] um das Anderthalbfache schneller als im dritten [Teil bewegt werde] und folgerichtig so weiter, [dann] wird der Raum, der in der gesamten Stunde durchquert wurde, unendlich sein.“229
3. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach irgendeinem suprapartienten Verhältnis geteilt wäre, und stetig die Geschwindigkeiten der verhältnismäßigen Teile, die unmittelbar [folgen, ins Verhältnis zueinander gesetzt werden, und] sich [dann] nämlich die Geschwindigkeit des kleineren Teils zur Geschwindigkeit des größeren [Teils] sich in irgendeinem vielfachen oder vielfach superpartikularen oder vielfach suprapartienten Verhältnis verhält, [dann] wird der Raum, der in der gesamten Stunde durchquert wurde, unendlich sein.“230
7. conclusio:
„Wenn eine Stunde in verhältnismäßige Teile nach einem beliebigen Verhältnis geteilt wurde, sich ein Bewegliches stetig schneller in dem folgenden [Teil] als in dem vorhergehenden Teil bewegt, nichtsdestoweniger schneller um ein Verhältnis, das kleiner ist als das Verhältnis der Teilung, [dann] wird sich der Raum, der in der gesamten Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde, in dem Verhältnis verhalten, durch das irgend ein gesamtes [Subjekt], das nach dem Verhältnis geteilt ist, durch das das größere Verhältnis der Zeit das Verhältnis der Geschwindigkeiten übertrifft, sich in der Ordnung zu dem ersten verhältnismäßigen Teil verhält.“231
1. Korollar: „Wenn eine Teilung einer Stunde in verhältnismäßige Teile nach einem vierfachen Verhältnis geschehen ist, und sich die Geschwindigkeiten stetig in einem doppelten Verhältnis befinden, so dass [das Verhältnis] der Geschwindigkeit des zweiten verhältnismäßigen Teils zu der Geschwindigkeit des ersten [Teils] ein doppeltes Verhältnis sei, und das [Verhältnis] der Geschwindigkeit des dritten [Teils] zur Geschwindigkeit des zweiten [Teils] auch ein doppeltes Verhältnis sei und so weiter, ist der Raum, der in der gesamten Stunde durchquert wurde, doppelt in Bezug auf den Raum, der im ersten verhältnismäßigen Teil durchquert wurde.“232
2. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem siebenviertelfachen Verhältnis geteilt wurde, sich die Geschwindigkeit eines beliebigen Teils zu der Geschwindigkeit des größeren Teils, der unmittelbar vorhergeht, in einem anderthalbfachen Verhältnis verhält, [dann] verhält sich der Raum, der in der gesamten Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde, in einem siebenfachen Verhältnis. Und wenn in dem ersten Teil ein Fuß absolviert wurde, werden in der gesamten Stunde sieben Fuß absolviert.“233
8. conclusio:
„Wenn eine Stunde in verhältnismäßige Teile nach einem beliebigen Verhältnis aufgeteilt werde, und in einem feststehenden Verhältnis ein Bewegliches stetig schneller in dem größeren vorhergehenden Teil als in dem kleineren unmittelbar folgenden [Teil] bewegt werde, [dann] wird sich der Raum, der in der gesamten Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde, in dem Verhältnis verhalten, in dem sich irgendein gesamtes [Subjekt], das in verhältnismäßige Teile nach einem Verhältnis geteilt ist, das aus dem Verhältnis der Zeit – nämlich [dem Verhältnis] des größeren verhältnismäßigen Teils zum kleineren unmittelbar folgenden Teil – und [dem Verhältnis] der Geschwindigkeit des größeren Teils zur Geschwindigkeit des kleineren Teils zusammengesetzt ist, zu dem ersten verhältnismäßigen Teil einer solchen Teilung verhalten.“234
1. Korollar: „Wenn eine Aufteilung einer Stunde in verhältnismäßige Teile nach einem fünfdrittelfachen Verhältnis geschehen ist, und [es] im ersten verhältnismäßigen Teil irgendein Bewegliches mit irgendeiner Geschwindigkeit bewegt werde, und im zweiten [Teil] mit einer um das Fünfdrittelfache niedrigeren [Geschwindigkeit bewegt werde], und [es] im dritten [Teil] mit einer um dasselbe Fünfdrittelverhältnis niedrigeren Geschwindigkeit als im zweiten [Teil bewegt werde] und so weiter, dann verhält sich der Raum, der in der gesamten Stunde durchquert worden ist, zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde, in einem siebenviertelfachen Verhältnis. Das ist von 7 zu 4.“235
2. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem doppelten Verhältnis geteilt wurde, und sich ein Bewegliches stetig um das Doppelte langsamer in dem folgenden kleineren Teil als in dem unmittelbar vorhergehenden, größeren Teil bewegt, [dann] verhält sich der Raum, der in der gesamten Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen Teil der Stunde durchquert wurde, in einem vierdrittelfachen Verhältnis.“236
3. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem dreifachen Verhältnis geteilt wurde, und sich ein Bewegliches um das Vierfache langsamer im folgenden, kleineren Teil als in dem ihm unmittelbar vorhergehenden [Teil] bewegt, [dann] wird sich der Raum, der in der gesamten Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde, in einem zwölfelftelfachen Verhältnis verhalten. Wenn es im ersten [Teil] einen Fuß durchquert, wird es in der gesamten Stunde zwölf Elftel eines Fußes absolvieren.“237
9. conclusio:
„Wenn eine Stunde in verhältnismäßige Teile nach einem beliebigen Verhältnis geteilt wurde, und ein Bewegliches in einem feststehenden Verhältnis in einem beliebigen geraden, nachfolgenden Teil als in dem geraden, unmittelbar ihm vorhergehenden Teil schneller bewegt werde, und ebenso in einem fest stehenden, gleichen, größeren oder kleineren Verhältnis stetig in einem beliebigen ungeraden folgenden Teil schneller als in dem ungeraden, unmittelbar vorhergehenden [Teil] bewegt werde, [dann] wird der Raum, der in der gesamten Stunde durchquert wurde, unendlich sein, solange das Verhältnis der Geschwindigkeiten dem Verhältnis der Zeiten gleich ist oder größer. Und wenn das Verhältnis der Geschwindigkeiten der geraden Teile und das Verhältnis der Geschwindigkeiten der ungeraden Teile kleiner als das Verhältnis der Zeiten wären, dann verhält sich der Raum, der in allen geraden Teilen durchquert wurde, zu dem Raum, der im ersten der geraden [Teile] durchquert wurde, in dem Verhältnis, in dem sich irgendein [Körper], der in verhältnismäßige Teile nach dem Verhältnis geteilt wurde, durch das das Verhältnis der Zeiten das Verhältnis der Geschwindigkeiten übertrifft, zu dem ersten verhältnismäßigen Teil des gesamten [Körpers] verhält. Und auf ähnliche Weise muss es über den Raum, der in allen ungeraden Teile durchquert wurde, gesagt werden.“238
1. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem doppelten Verhältnis aufgeteilt wurde, und im ersten [Teil] von ihnen ein Bewegliches mit irgendwie großen Geschwindigkeit gleichförmig bewegt werde, und im zweiten [Teil so] bewegt werde, dass es seine Bewegung gleichförmig von der Stufe, mit der es im ersten [Teil] bewegt wurde, bis zur doppelten Stufe erhöht, und im dritten [Teil] mit der doppelten Stufe gleichförmig bewegt werde, und im vierten [Teil] es gleichförmig seine Bewegung von der doppelten Stufe bis zur von ihr doppelten Stufe erhöht werde, so dass es in allen ungeraden Teilen stetig gleichförmig um das Doppelte schneller im folgenden ungeraden [Teil] als im unmittelbar vorhergehenden ungeraden [Teil] bewegt werde, und in einem beliebigen geraden Teil [so] bewegt werde, dass es seine Bewegung gleichförmig von der Stufe des ungeraden, unmittelbar vorhergehenden Teil bis zur Stufe des ungeraden, unmittelbar folgenden [Teils] erhöht, so dass die Geschwindigkeiten der ungeraden Teile bis zur Gleichförmigkeit vermindert werden, [und] auch wenn sie sich stetig in einem doppelten Verhältnis zueinander verhalten, dann wird sich der gesamte Raum, der in der Stunde durchquert wurde, in einem siebeneinhalbfachen Verhältnis zu dem Raum verhalten, der im ersten ungeraden verhältnismäßigen Teil durchquert wurde.“239
2. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem doppelten Verhältnis geteilt wurde, und im ersten Teil ein Bewegliches gleichförmig mit einer irgendwie großen Geschwindigkeit bewegt werde, und es im zweiten [Teil] seine Bewegung gleichförmig von der Stufe, mit der es im ersten [Teil] bewegt wurde, bis zum Dreifachen erhöhe, und im dritten [Teil] gleichförmig mit jener dreifachen Stufe bewegt werde, und es im vierten [Teil so] bewegt werde, dass es seine Bewegung gleichförmig von der Stufe, mit der es im dritten [Teil] bewegt wurde, bis zum Dreifachen von dieser erhöht, und folgerichtig immer in einem beliebigen geraden die Stufe des unmittelbar vorhergehenden, ungeraden [Teils] bis zum Dreifachen derselben Stufe gleichförmig erhöht, [dann] wird sich der Raum, der in der gesamten Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen ungeraden Teil durchquert wurde, in einem vierundzwanzigdreizehntelfachen Verhältnis verhalten.“240
3. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem vierfachen Verhältnis geteilt wurde, und ein Bewegliches in einem beliebigen folgenden, ungeraden Teil um das Vierfache schneller bewegt werde als im unmittelbar vorhergehenden, ungeraden [Teil], und in einem beliebigen folgenden, geraden [Teil] um das Vierfache schneller als in dem unmittelbar vorhergehenden, geraden [Teil], und um das Doppelte schneller im ersten geraden Teil als im ersten ungeraden [Teil], dann verhält sich der gesamte Raum, der in einer Stunde durchquert wurde, zu dem Raum, der im ersten verhältnismäßigen, ungeraden Teil durchquert wurde, in einem doppelten Verhältnis.“241
Es folgt eine Aufzählung von Möglichkeiten für weitere Korollare, die hier aber nicht ausgeführt beziehungsweise bewiesen werden.
10. conclusio:
„Wenn eine Stunde in verhältnismäßige Teile nach einem doppelten Verhältnis geteilt wurde, und das Bewegliche A im ersten verhältnismäßigen Teil mit einer irgendwie großen Geschwindigkeit bewegt werde, und [A] im zweiten [Teil] mit einer um das anderthalbfache größeren Geschwindigkeit [bewegt werde], und [A] im dritten [Teil] mit einem um das Fünfviertelfache größeren Geschwindigkeit als im ersten [Teil bewegt werde], und [A] im fünften [Teil] mit einer um das Elfzehntelfache größeren als im ersten [Teil bewegt werde] und so folgerichtig weiter, in dem man über die species eines superpartikularen Verhältnisses vorwärts geht, das von pariter pares Zahlen bestimmt wird –dennoch könnte man besser sagen durch Absteigen, denn die suprapartikularen Verhältnisse werden kleinere [Verhältnis], je mehr sie von einer größeren Zahl bestimmt werden, das heißt von einem irgendwievielten Teil, der von der größeren Zahl bestimmt wird – [dann] der Raum, der in der gesamten Stunde durchquert wurde, verhält sich zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde, in einem siebendrittelfachen Verhältnis.“242
1. Korollar: „Wenn die Stunde nach einem doppelten Verhältnis geteilt wäre, und im ersten der Teile irgendein Bewegliches mit einer irgendwie hohen Geschwindigkeit bewegt werde, und [es] im zweiten [Teil] mit einer um das Siebenviertelfache höheren Geschwindigkeit [bewegt werde], und [es] im dritten [Teil] mit einer um das Elfachtelfache höheren Geschwindigkeit als im ersten [Teil bewegt werde], und [es] im vierten [Teil] mit einem um das Neunzehnsechzehntelfache höheren Geschwindigkeit als im ersten [Teil bewegt werde], und [es] im fünften [Teil] mit einer um das Fünfunddreißigzweiunddreißigstelfache höheren Geschwindigkeit als im ersten [Teil bewegt werde] und folgerichtig so weiter, indem man vorwärts durch die species eines Verhältnisses geht, dessen [größere Zahl drei Zahlen größer als die kleinere Zahl ist] – sie wurden bestimmt von pariter pares Zahlen oder von irgendwievielten Teilen, die von diesen Zahlen bestimmt werden – [dann] ist der Raum, der in der gesamten Zeit durchquert wurde, fünfhalbefach in Bezug auf den Raum, der im ersten verhältnismäßigen Teil durchquert wurde.“243
2. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem doppelten Verhältnis geteilt wurde, und im ersten [Teil] von ihnen irgendein Bewegliches mit irgendeiner Geschwindigkeit bewegt werde, und [es] im zweiten [Teil] von ihnen mit einer um das Vierdrittelfache höheren [Geschwindigkeit bewegt werde], und [es] im dritten [Teil] mit einer um das Siebensechstelfache höheren [Geschwindigkeit] als im ersten [Teil bewegt werde], und [es] im vierten [Teil] mit einer um das Siebzehnsechzehntelfache höheren [Geschwindigkeit] als im ersten [Teil bewegt werde] und so folgerichtig weiter, in dem man mit geraden Zahlen aufsteigt, die sich stetig in einem doppelten Verhältnis zueinander verhalten, und von der Zahl Drei angefangen wird – das bedeutet mit den species eines superpartikularen Verhältnisses, die bestimmt werden von irgendwievielten Teilen, die von jenen Zahlen bestimmt werden – [dann] ist der in der gesamten Stunde durchquerte Raum zwanzigneuntelfach in Bezug auf den Raum, der im ersten verhältnismäßigen Teil durchquert wurde.“244
11. conclusio:
„Wenn eine Stunde in verhältnismäßige Teile nach einem beliebigen Verhältnis geteilt wurde, und im ersten [Teil] ein Bewegliches mit einer irgendwie hohen Geschwindigkeit bewegt werde, und [es] im zweiten [Teil] mit einer um das Anderthalbfache höheren [Geschwindigkeit bewegt werde], und [es] im dritten [Teil] mit einer um das Vierdrittelfache höheren [Geschwindigkeit] als im zweiten [Teil bewegt werde], und [es] im vierten [Teil] mit einer um das Fünfviertelfache höheren [Geschwindigkeit] als im dritten [Teil bewegt werde], und [es] im fünften [Teil] mit einer um das Sechsfünftelfache höheren [Geschwindigkeit] als im vierten [Teil bewegt werde] und folgerichtig so weiter, und wenn keine allgemeine Regel ausgezeichnet werden kann, um den in der gesamten Stunde durchquerten Raum zu finden, kann nichtsdestoweniger dennoch durch die Auszeichnung nach einer beliebigen species für die Teilung der Stunde mit Sicherheit ein in der gesamten Stunde durchquerter Raum herausgefunden werden und sein Verhältnis zu dem Raum, der im ersten verhältnismäßigen Teil durchquert wurde.“245
12. conclusio:
„Wenn irgendeine Zeit in verhältnismäßige Teile nach einem doppelten Verhältnis geteilt werden würde, und [es] im ersten verhältnismäßigen Teil ein Bewegliches mit einer beliebig großen Geschwindigkeit bewegt werde, und [es] im zweiten [Teil] um das Doppelte schneller als im ersten [Teil bewegt werde], und [es] im dritten [Teil] um das Anderthalbfache schneller als im ersten [Teil bewegt werde], und [es] im vierten [Teil] um das Vierdrittelfache schneller als im ersten [Teil bewegt werde] und folgerichtig so weiter, wenn man über alle species eines superpartikularen Verhältnisses vorwärts aufsteigt, [dann] ist der Raum, der in der gesamten Zeit durchquert wurde, mehr als das Doppelte größer in Bezug auf den Raum, der im ersten verhältnismäßigen Teil durchquert wurde, und kleiner als das Vierfache.“246
1. Korollar: „Wenn die Zeit in verhältnismäßige Teile nach einem anderthalbfachen Verhältnis geteilt werden würde, und ein Bewegliches auf dieselbe Weise bewegt werde, wie es in dem Beispiel der conclusio gesagt wurde, [dann] wird der Raum, der in der gesamten Stunde bewegt wurde, größer als das Dreifache sein in Bezug auf den Raum, der im ersten verhältnismäßigen Teil durchquert wurde, und nicht weniger als das Achtfache.“247
2. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem fünfdrittelfachen Verhältnis geteilt wurde, und ein Bewegliches im ersten verhältnismäßigen Teil mit einer beliebig großen Geschwindigkeit bewegt wurde, und [es] im zweiten [Teil] um ein siebenviertelfaches Verhältnis schneller [bewegt werde], und [es] im dritten [Teil] um ein elfachtelfaches Verhältnis schneller als im zweiten [Teil bewegt werde], und [es] im vierten [Teil] um ein neunzehnsechzehntelfaches Verhältnis schneller als im dritten [Teil bewegt werde] und folgerichtig so weiter, wird der Raum, der in der gesamten Stunde durchquert wurde, größer sein als das Fünfhalbefache in Bezug auf den Raum, der im ersten verhältnismäßigen Teil durchquert wurde, und kleiner als das Fünfundsechzigviertelfache.“248
3. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem dreifachen Verhältnis geteilt wurde, und ein Bewegliches im ersten verhältnismäßigen Teil mit einer beliebig hohen Geschwindigkeit bewegt werde, und [es] im zweiten [Teil] mit einer um das Fünfdrittelfache höheren Geschwindigkeit [bewegt werde], und [es] im dritten [Teil] mit einer um das Siebenfünftelfache höheren Geschwindigkeit als im ersten [Teil bewegt werde], und [es] im vierten [Teil] mit einer um das Neunsiebentelfache höheren [Geschwindigkeit] als im ersten [Teil bewegt werde], und [es] im fünften [Teil] mit einer um das Elfneuntelfache höheren [Geschwindigkeit] als im ersten [Teil bewegt werde] und so folgerichtig weiter, indem man nach den species eines suprabipartienten Verhältnisses aufsteigt, die bestimmt werden von ungeraden Zahlen oder von irgendwievielten Teilen, die von ungeraden Zahlen bestimmt werden, [dann] ist der Raum, der in der gesamten Stunde durchquert wurde, größer als das Anderthalbfache in Bezug auf den Raum, der im ersten verhältnismäßigen Teil durchquert wurde, und weniger als der Neunviertelfache.“249
4. Korollar: „Wenn eine Stunde in verhältnismäßige Teile nach einem vierfachen Verhältnis geteilt wurde, und im ersten verhältnismäßigen Teil ein Bewegliches mit einer beliebig großen Geschwindigkeit bewegt werde, und [es] im zweiten [Teil] um das Anderthalbfache schneller [bewegt werde], und [es] im dritten [Teil] um das Fünfdrittelfache schneller als im ersten [Teil bewegt werde], und [es] im vierten [Teil] um das Siebenviertelfache schneller als im ersten [Teil bewegt werde], und [es] im fünften [Teil] um das Siebenfünftelfache schneller als im ersten [Teil bewegt werde], und [es] im sechsten [Teil] um das Elfachtelfache schneller als im ersten [Teil bewegt werde] und folgerichtig so weiter, indem man über die ungeraden Teile durch ein supratripartientes Verhältnis aufsteigt und bei den geraden [Teilen] durch ein suprabipartientes [Verhältnis], [dann] ist der Raum, der in der gesamten Stunde durchquert wurde, mehr als das Vierdrittelfache in Bezug auf den Raum, der im ersten verhältnismäßigen Teil durchquert wurde, und weniger als das Sechszehnneuntelfache in Bezug auf den Raum, der im ersten [Teil] durchquert wurde.“250
Es folgen auf mögliche Einwürfe gegen die 12. conclusio zwei propositiones von Alvarus Thomas:
1. propositio:
„Wenn eine Geschwindigkeit, die bis ins Unendliche ungleichförmig ist, irgendeiner Kohärenz oder einem Verhältnis stetig dient, ist es leicht, die gesamte Geschwindigkeit zu bemessen und den Raum, der mit der dazwischen liegenden [Geschwindigkeit] durchquert wird, zu berechnen.“251
2. propositio:
„Wenn sich ungleichförmige Geschwindigkeiten nicht stetig untereinander in irgendeinem Verhältnis befinden, wie es in dem Beispiel der zwölften conclusio und der folgenden Korollare ist, [dann] ist es unmöglich, dass ein Verstand endlichen Kapazität natürlicherweise eine solche ungleichförmige Geschwindigkeit bis zur Gleichförmigkeit berechnet und unfehlbar den genauen Raum, der durchquert wurde, auszeichnet.“252
exemplum: „Wenn eine Stunde in verhältnismäßige Teile nach einem doppelten Verhältnis geteilt wurde, und ein Bewegliches im ersten verhältnismäßigen Teil beliebig schnell bewegt werde, und [es] im zweiten [Teil] um das Anderthalbfache schneller [bewegt werde], und [es] im dritten [Teil] um das Sechsfünftelfache [schneller bewegt werde], und [es] im vierten [Teil] um das Neunachtelfache [schneller] als im ersten [bewegt werde], und folgerichtig so weiter, indem man nach den species eines interskalaren superpartikularen Verhältnisses aufsteigt und stetig zwei auslässt.“253 Und weiter: „Ebenso wenn die Stunde in verhältnismäßige Teile nach einem dreifachen Verhältnis geteilt wäre, das Bewegliche A im ersten verhältnismäßigen Teil beliebig schnell bewegt werde, und [es] im zweiten [Teil] um das Sechsfünftelfache schneller [bewegt werde], und [es] im dritten [Teil] um das Zehnneuntelfache schneller als im ersten [Teil bewegt werde], und [es] im vierten [Teil] um das Vierzehndreizehntelfache schneller als im ersten [Teil bewegt werde], und [es] im fünften [Teil] um das Achtzehnsiebzehntelfache schneller als im ersten [Teil bewegt werde], und folgerichtig so weiter, indem man nach den species eines superpartikularen Verhältnisses aufsteigt und drei stetig auslässt, [und] ebenso durch ein solches Aufsteigen, indem man vier stetig auslässt, ebenso beim stetigen Auslassen von Fünf, von 6 und von 7 und folgerichtig so weiter, [dann] werden sich so unendliche, ungleichförmige Geschwindigkeiten ergeben, deren Einförmigkeit von uns in keiner Weise natürlich gefunden werden kann.“254
responsio nach der propositio von Nikolaus Oresme:
„Wo auch immer eine Vielzahl von Verhältnissen auftritt, zwischen denen nicht leicht ein Verhältnis gefunden wird, muss man beurteilen, ob sie irrational zueinander sind, und daher [auch] die durchquerten Räume irrational sind.“255 Und weiter: „Wenn daher ein solches Beispiel vorgeschlagen wird, muss man antworten, dass der in der gesamten Stunde durchquerte Raum nicht kommensurabel zu dem Raum ist, der im ersten verhältnismäßigen Teil durchquert wurde.“256 Es folgt eine Polemik gegen Richard Swineshead.
responsio in Form einer Polemik:
„Ich antworte, dass ich bei einer ähnlichen Beschäftigung urteile, dass eine verdoppelte Vorsicht aufgebracht werden muss.“257
1. „Zuerst werde für die Erheiterung und zum Kichern das Argument von ihm für so unnütz und unverständlich erachtet. Und man erbitte Feder und Tinte, damit durch die species der Multiplikation und durch die übrigen species eines Algorithmus die intensio der Geschwindigkeit in dem von ihm vorgeschlagenen Beispiel berechnet werden kann.“258
2. „Man sage kurz zu dem, der streitet, dass eine solche Geschwindigkeit nicht unfehlbar und mit Sicherheit berechnet werden kann, und ferner auch viele andere ungleichförmige Geschwindigkeiten nicht auf natürliche Weise bis zur Gleichförmigkeit vermindert werden können. Und wenn er laut den, der antwortet, bekämpfen will, in dem das Gegenteil er versichert, schlägt der Antwortende ihm ein ähnliches Beispiel vor und sagt ihm, dass er ihm zusichere, dass der Raum genau mit einer solchen dazwischen liegenden Geschwindigkeit durchquert wurde. Und wenn er sagen würde, dass es nicht möglich ist, auf natürliche Weise die genaue Geschwindigkeit in einem solchen Beispiel zu finden, dann füge der Antwortende hinzu, dass dies auch nicht bei seinem [Beispiel] auf ähnliche Weise mit einer gleichen ratio [möglich sei]. Wenn der Gegner aber sage, dass er einen solchen Raum nicht auszeichnen wolle, obwohl er auf natürliche Weise aufzeigbar sei, dann würde der Antwortende ihm dasselbe sagen.“259
conclusio responsiva:
„Jede gleichförmig ungleichförmige Bewegung nach der Zeit hat nach der mittleren Stufe bemessen zu werden, und jede ungleichförmig ungleichförmige [Bewegung] nach der Zeit [hat] gemäß der reductio bis zur Gleichförmigkeit oder gemäß der Berechnung der denominatio [bemessen zu werden], und wenn es nicht in keinem Beispiel [so ist], ist es schwierig oder unmöglich, auf natürliche Weise zulässig und unfehlbar die Geschwindigkeit zu berechnen.“260
Zuletzt die rationes ante oppositium:
Zur 1. ratio ante oppositum:
„In Bezug auf die erste [ratio] wurde dort bis zu letzten replica geantwortet, auf die ich antworte, indem ich die sequela zugestehe und die Falschheit des Nachsatzes verneine. Auch wenn bewiesen wird, dass sonst folgen würde, dass ein Bewegliches, das stetig unendlich schnell seine Bewegung erhöht, unendlich langsam bewegt wird, verneine ich jene sequela. Und bei dem Beweis gestehe ich das Beispiel zu. Und bei dem Argument gestehe ich den Vordersatz zu, indem ich ,das Unendliche‘ in einem größeren und einem kleineren [Sinne] synkathegorematisch auffasse. Und ich verneine die Schlussfolgerung.“261
1. Korollar: „In dem vorgeschlagenen Beispiel wird ein beliebiges [Bewegliches] von ihnen unmittelbar danach mit unendlicher Langsamkeit bewegt werden, und dennoch wird irgendeines von ihnen unmittelbar danach mit unendlicher Schnelligkeit bewegt werden.“262
2. Korollar: „In dem dargelegten Beispiel wird ein beliebiges [Bewegliches] von ihnen unmittelbar danach einen bis ins Unendliche kleinen Raum in irgendeiner Zeit durchqueren. Und dennoch wird unmittelbar danach irgendein [Bewegliches] von ihnen einen bis ins Unendliche großen Raum in irgendeiner Zeit durchqueren.“263
3. Korollar: „Unmittelbar danach wird ein [Bewegliches] von ihnen mit unendlicher Langsamkeit bewegt werden. Und kein [Bewegliches] von ihnen wird unmittelbar danach so langsam wie A bewegt werden. Und A wird bewegt werden, und A wird nicht unmittelbar danach mit unendlicher Langsamkeit bewegt werden.“264
Zur 1. confirmatio sagt Alvarus Thomas: „Dazu antworte ich, indem ich die sequela verneine, sage ich vielmehr, dass es möglich ist, dass eine Bewegung in begrenzter Zeit geometrisch gleich schnell erhöht wird, wie eine andere [Bewegung] mit denselben, von Anfang an existierenden, gleichen [Bedingungen] vermindert wird. Aber es ist notwendig, dass die [Bewegung], die erhöht wird, eine unendliche Geschwindigkeit in einer begrenzten Zeit erwirbt, in der die andere Bewegung bis zu keiner Stufe vermindert wird.“265
Zur 2. confirmatio: „Ich antworte, indem ich die sequela verneine, und vielmehr sage: Wenn eine [Bewegung] bis zum durch 2 Geteilten vermindert wurde, wurde die andere bis zu keiner Stufe vermindert.“266 Und weiter: „Und die ratio ist: Das Bewegliche reicht nicht bei der Bewegung aus, um um das Doppelte schneller als das andere [Bewegliche] bewegt zu werden. Denn wir sprechen hier nicht über eine geometrische Geschwindigkeit, sondern über eine arithmetische [Geschwindigkeit], die gemäß der verlorenen latitudo und nicht nach dem verlorenen Verhältnis ermittelt werden muss. Und so muss es immer erfasst werden, wenn man ,gleich schnell‘ sagt, sofern nicht ,proportional‘ oder ,geometrisch‘ hinzugefügt wird.“267
Bei der 3. confirmatio verneint er die sequela.268
Zur 4. confirmatio heißt es: „In Bezug auf die vierte confirmatio wurde bis zur letzten replica geantwortet, auf die die siebente propositio der ersten notabile dieser quaestio mit den dort dargelegten Annotationen antwortet.“269
Zur 2. ratio ante oppositum:
Alvarus Thomas stimmt der sequela zu, verneint aber deren consequentia und die consequentia des Beweises. Bei der replica gesteht er die sequela zu, er verneint aber, dass der Nachsatz falsch ist.270
Zur 3. ratio ante oppositum:
Die sequela wird von Alvarus Thomas verneint. Und weiter heißt es: „Vielmehr sage ich, dass eine feststehende intensio in dem dargelegten Beispiel in dem Argument gegeben werden wird. Aber die [intensio] wird nicht rational in Bezug auf die intensio der Geschwindigkeit des ersten Teils sein.“271 Er folgt der ersten replica.272
Zur 4. ratio ante oppositum:
Die Antwort steht laut Alvarus Thomas in der replica der 4. ratio.273
Kapitel 3.2.4
Im letzten Kapitel des zweiten Traktats verbindet Alvarus Thomas die Fragen zur Berechnung von Geschwindigkeiten ungleichförmiger Bewegungen quoad subjectum und quoad tempus. Er bezeichnet solche Bewegungen, in denen sich diese Parameter zugleich ändern, als motus mixti.
quaestio:
„Gefragt wird also, woran gleichwie nach der Wirkung einer ungleichförmigen Bewegung in Bezug auf die Zeit und das Subjekt zugleich die Geschwindigkeit einer vermischten Bewegung nach der Zeit und nach dem Subjekt zugleich einer ungleichmäßigen Bewegung ermittelt zu werden hat, ob zum Beispiel die Geschwindigkeit einer ungleichförmige Bewegung nach der Zeit und dem Subjekt zugleich gemäß der Linie bemessen werden müsse, die von einer dazwischen liegenden gleichförmigen Bewegung beschrieben wurde, zu der eine solche ungleichförmige Geschwindigkeit vermindert zu werden hat, und ob die Geschwindigkeit einer vermischten Bewegung gemäß dem Raum ermittelt zu werden hat, der aus den Räumen zusammengesetzt ist, die von mehreren dazwischen liegenden Bewegungen durchquert wurden, durch die das Bewegliche zugleich bewegt wird, das durch eine vermischte Bewegung bewegt wird.“274
1. ratio:
„Die Geschwindigkeit einer ungleichförmigen Bewegung nach der Zeit und dem Subjekt zugleich hat nicht nach der beschriebenen Linie und so weiter ermittelt zu werden.“275
sequela:
„Denn wenn es so [wäre], würde daraus folgen, dass die genaue Geschwindigkeit einer solchen Bewegung gemäß der reductio bis zur Gleichförmigkeit bemessen werden muss. Aber der Nachsatz ist falsch.“276 Daraus schließt Alvarus Thomas letztendlich:
„Die ratio gilt, weil das Rad mit einer doppelten Bewegung bewegt wird, indem es durch beide von ihnen einen Raum beschreibt, nämlich durch eine Kreisbewegung oder durch eine solche, die die Natur einer Kreisbewegung hat. (Denn es wird stetig um dieselbe Achse bewegt, obwohl es die Kreislinie nicht geeignet beschreibt, wie weiter oben gesagt worden ist.) Und darüber wird ein Punkt bewegt, von dessen Geschwindigkeit die gesamte Geschwindigkeit des Rads genommen wird, indem er sich durch die Bewegung der rarefactio stetig vom Mittelpunkt zurückzieht. Daher muss die Geschwindigkeit des Punkts und folgerichtig des Rads gemäß der Linie bemessen werden, die aus der Linie, die der Punkt ohne die rarefactio beschreibt, und gemäß der sehr kurzen Linie zusammengerechnet wurde, durch die er mehr vom Mittelpunkt entfernt ist, als er vor der rarefactio entfernt war.“277
In oppositum:
„Aber dagegen [kann gesprochen werden], weil dann folgen würde: Wenn das Rad B beginnen würde, kreisförmig mit dem mitteleren Punkt bewegt zu werden, von dessen Geschwindigkeit – wie ich annehme – die Geschwindigkeit des gesamten Rads bemessen werden muss, und er bewege sich im ersten verhältnismäßigen Teil der Stunde, die nach einem vierfachen Verhältnis geteilt wurde, mit einer Geschwindigkeit wie 4, und im zweiten [Teil] um das Doppelte schneller, und im dritten [Teil] um das Doppelte schneller als im zweiten [Teil] und folgerichtig so weiter. Und wenn in einem beliebigen verhältnismäßigen Teil das Rad gleichförmig so ausgedünnt werden würde, dass der mittlere Punkt in einem beliebigen verhältnismäßigen Teil einen Fuß Abstand erwirbt, den es zum Abstand vom Mittelpunkt hat, dann würde das Rad in genau der Stunde auf endliche Weise die Linie beschreiben, die im ersten verhältnismäßigen Teil beschrieben wurde. Gemäß dem Nachsatz ist das falsch.“278 Und weiter: „Also folgt, dass er in der gesamten Stunde genau den doppelten Raum in Bezug auf den Raum durchquert, der im ersten verhältnismäßigen Teil durchquert wurde.“279
2. ratio in Form einer sequela:
„Wenn der Teil wahr wäre, würde folgen, dass irgendein Bewegliches in irgendeiner Zeit stetig seine Bewegung beinahe bis zu keiner Stufe vermindern würde und dennoch stetig in derselben Zeit immer schneller den Raum durchqueren würde. Aber das scheint es zu berühren. Daher [ist es auch] das, woraus er folgt.“280
probatio ad exemplum: „Und ich lege dar, dass Sokrates in irgendeinem Schiff gegen denselben Unterschied bewegt werde, gegen den das Schiff von irgendeiner Stufe bewegt wird, indem er stetig seine Bewegung bis zu keiner Stufe vermindert, während das Schiff stetig seine Bewegung von derselben Stufe aus schneller erhöht, als Sokrates sie vermindert. Nachdem das dargelegt wurde, vermindert Sokrates stetig seine Bewegung, und zwar bis zu keiner Stufe. Und dennoch durchquert er immer schneller in derselben Zeit den Raum. Was zu beweisen war. Daher der Vorschlag. Der Obersatz ist offensichtlich, und der Untersatz wird bewiesen. Denn stetig ist die Geschwindigkeit immer höher, die vermischt wurde oder aus der eigenen Geschwindigkeit, durch die Sokrates bewegt wird, und aus der Geschwindigkeit des Schiffs zusammengesetzt ist, weil es stetig eine höhere Geschwindigkeit erwirbt, als er sie in dem Beispiel verliert. Daher durchquert er stetig immer schneller den Raum. Was zu beweisen war.“281
In oppositum in Form einer sequela:
„Aber dagegen [kann gesagt werden], weil dann [dies] folgen würde: Es stünde fest, dass Sokrates kaum ermüden würde, indem es gelingt, ohne Hindernis bewegt zu werden, wenn vielmehr Sokrates die beste dispositio zum Laufen und zum Bewegt Werden habe, und dennoch überhaupt nicht bewegt werden würde. Aber das ist falsch.“282
3. ratio:
„Es gibt keine vermischte Bewegung.“283 Und weiter: „Wenn es irgendeine vermischte Bewegung gäbe, wäre sie im Besonderen aus dem Aufstieg und dem Abstieg zusammengesetzt. Aber keine solche [vermischte Bewegung] ist angebbar.“284
probatio in Form einer sequela: „Wenn irgendeine solche [Bewegung] angebbar wäre, würde folgen, dass ein endlicher Körper angebbar wäre, von dem ein Teil aufsteige und der andere [Teil] absteige. Und das Übrige würde so ununterbrochen durch seine natürliche dispositio bewegt werden. Dabei steigt ein Teil von ihm stetig auf und der andere steigt ab. Aber der Nachsatz ist falsch.“285
exemplum pro probatione: „Und ich lege das Beispiel dar, dass die Erde durch den Mittelpunkt der Welt von Osten nach Westen durchbohrt sei. Und man erfasse den Erdkreis, der eine gleichförmige Schwere hat, oder irgendeine andere Figur. (Es kommt auf dasselbe hinaus.) Und jene[s Stück] Erde steige durch die Bohrung bis zum Mittelpunkt der Welt ab. Die Bohrung hinterlässt eine Leere. Und Gott erlaubt, dass die Erde so lange bewegt wird, wie sie ein Verhältnis größerer Ungleichheit zum Bewegen haben würde.“286
Pro solutione gibt Alvarus Thomas drei notabilia an:
1. notabile:
„Bei jeder ungleichförmigen Bewegung nach der Zeit und nach dem Subjekt zugleich darf die Geschwindigkeit gemäß der reductio nicht einmal bis zur Gleichförmigkeit der denominatio bemessen werden.“287
Und er führt weiter aus: „Dennoch muss dieses Eine beachtet werden, dass eine ungleichförmige Bewegung nach der Zeit und nach dem Subjekt zugleich geschieht, wenn eine andere Bewegung des Subjekts abgesondert wurde, nämlich einer rarefactio oder einer Verdichtung, zum Beispiel wenn ein Rad, das nicht ausgedünnt oder verdichtet wurde, immer schneller oder immer langsamer bewegt wird. Aber manchmal geschieht eine solche Bewegung und eine rarefactio oder eine Verdichtung oder eine Verbreiterung und so weiter begleitet sie. Auf die erste Weise muss nun die Geschwindigkeit einer solchen Bewegung zuerst gemäß der Geschwindigkeit bemessen werden, durch die der mittlere Punkt bewegt wird oder der am schnellst bewegt wird – folgt man der Verschiedenheit der opiniones auf die Weise [beurteilt werden], wie es weiter oben über die ungleichförmige Bewegung nach dem Subjekt allein gesagt wurde. Die Geschwindigkeit der Bewegung muss gemäß der Linie bemessen werden, die von dem mittleren oder den am schnellsten bewegten Punkt eines solchen Körpers [aufgestellt ist]. Aber ein solcher Punkt wird mit einer zweifachen Bewegung bewegt, nämlich einer lokalen Bewegung und einer rarefactio oder einer Verdichtung und so weiter. Daher wird ein solcher Punkt eine so große Linie beschreiben, als ob er auf die erste Weise bewegt werden würde. Und darüber wird er eine Linie beschreiben, durch die er weiter vom Mittelpunkt einer solchen Bewegung entfernt ist, wenn es ausgedünnt werden würde, oder weniger [entfernt ist], wenn es verdichtet werden würde, als er vorher am Anfang der Bewegung entfernt war.“288
Und weiter: „Beachte hier dennoch hier, dass manchmal irgendein Bewegliches bewegt wird, und zwar mit einer geraden Bewegung und einer kreisförmigen [Bewegung] und einer rarefactio zugleich. Daher wird stetig der Mittelpunkt des Körpers bewegt. Das trifft so zu, wenn ein Ball oder irgend ein anderer sphärischer Körper oder mit einer anderen Figur mit einer geraden Bewegung und einer kreisförmigen [Bewegung] bewegt werde, indem er stetig kreist und stetig ausdünnt, und zwar darin. Und in einem ähnlichen Beispiel muss die Geschwindigkeit eines solchen Beweglichen gemäß der Geschwindigkeit des Mittelpunkts des Beweglichen beurteilt werden.“289
2. notabile:
Der Term motus mixtus, also eine vermischte Bewegung eines Körpers, die aus mehreren Bewegungen zusammengesetzt ist, kann zwei unterschiedliche Bedeutungen haben, der Alvarus Thomas noch eine dritte hinzufügt.290
1. Bedeutung:„Gemäß sich und einem beliebigen [Punkt] von ihm wird er von einer beliebigen jener Bewegungen von sich aus bewegt und nicht durch irgendeine [Bewegung] von ihnen in Bezug auf die Bewegung eines anderen [Beweglichen], wie wenn dasselbe zugleich mit einer lokalen Bewegung und der Bewegung einer alteratio bewegt wird.“291
2. Bedeutung: „Auf die zweite Weise soll irgendetwas mit einer aus mehreren Bewegungen vermischten Bewegung bewegt werden, die nicht gleich der ersten [Bewegung] sind, sondern durch eine Bewegung aus sich heraus und die andere in Bezug auf die Bewegung von anderen [Dingen] in der Art, dass eine der Bewegungen dem Beweglichen eigen sei und die andere [Bewegung] nicht.“292
3. Bedeutung: „Eine dritte Weise kann hinzugefügt werden. Sie besteht, wenn ein Teil [eines Körpers] aufsteigt und ein anderer [Teil desselben Körpers] absinkt.“293
„Daher muss die Geschwindigkeit einer solchen Bewegung gemäß dem Raum ermittelt werden, der zwischen einem fixierten und ruhenden Punkt und einem Punkt oder einer Begrenzung liegt, an dem ein solches Bewegliches am Ende der Bewegung ist. Das bedeutet gemäß der Linie, die von einem solchen Beweglichen zwischen jenen zwei Termen beschrieben wurde.“294
Dem fügt Alvarus Thomas vier Korollare hinzu, die Peter von Aliaco, Erzbischof von Cambray, aufgeschrieben hat:
1. Korollar: „Es ist möglich, aus zwei geraden [Bewegungen] eine kreisförmige Bewegung zu beschreiben. Das heißt, es ist möglich, dass irgendetwas mit einer zweifachen geraden Bewegung bewegt wird, indem es einen Kreis oder Teile eines Kreises beschreibt.“295
2. Korollar: „Aus zwei geraden Bewegungen kann in derselben Zeit eine vermischte Bewegung entstehen, die eine Seite irgendeines Quadrats und die Diagonale desselben [Quadrats] beschreibt.“296
3. Korollar: „Es ist möglich, dass dasselbe Bewegliche mit einer einfachen Bewegung bewegt wird, von der ein beliebiger Teil in einer vermischten Bewegung bewegt wird.“297
4. Korollar: „Es ist möglich, dass aus zwei regulären Bewegungen eine irreguläre [Bewegung] wird.“298
3. notabile:
„Beim Berühren des Stoffes des dritten Arguments – dessen Hauptfrage ist, ob die Erde, über die in dessen Beispiel eine Erwähnung gemacht wird, ununterbrochen so bewegt werde, dass das Übrige zu seiner natürlichen Disposition nicht so bewegt werden kann, dass sein Mittelpunkt der Mittelpunkt der Welt werde – [ist zu bemerken], dass mit dem Zeugnis des Philosophen im ersten [Buch] über den Himmer und der Erde ist der natürliche Ort des gesamten [Körpers] und [der natürliche Ort] eines Teils [des Körpers] dasselbe.“299 Und weiter: „Denn er sagt, dass bei jedem möglichen Ort irgendetwas durch die Natur begonnen wurde, bewegt zu werden, und an demselben [Ort] begonnen wurde, [etwas] beliebiges gleicher Abstammung und ähnlicher Natur bewegt werden. Wenn daher irgendeine Erde in der Luft wäre und wenn das Hindernis [darunter] entfernt wurde, würde sie bis absinken, bis dessen Mittelpunkt [dann] der Mittelpunkt der Welt werden würde. Kein Teil jener Erde widersteht der Erde, damit ihr Mittelpunkt nicht der Mittelpunkt der Welt werde. Denn dassselbe ist das Streben von einem Teil und dem Gesamten, dessen Teil er ist, wie der Kalkulator ausreichend naturgemäß im Kapitel über den Ort des Elements einführt.“300
Davon leitet Alvarus Thomas ab, „dass nämlich nach der Durchbohrung der Erde, wie es in dem Beispiel des dritten Arguments dargelegt wird, erdiges Quadrat absinkt, wie es ebendort dargelegt wird, [und] wenn ein solcher Globus zum Mittelpunkt der Erde gelangt, der Teil, der über dem Mittelpunkt ist, dem Teil, der unter dem Mittelpunkt ist, widerstehen würde, damit er nicht absteige. Ununterbrochen würde dort ein solches Quadrat bewegt werden, wenn die übrigen Hindernisse und Hilfen abgeleitet wurden.“301
Um das zu beweisen, werden zwei suppositiones aufgestellt:
1. suppositio:
„Wenn ein solches Quadrat so absteigt, und ein Teil von ihm ist in der kleineren Hälfte des Quadrats über dem Mittelpunkt der Welt, der restliche Teil des gesamten Quadrats aber unter dem Mittelpunkt der Welt, ist der Teil, der gefangen ist zwischen dem Mittelpunkt der Welt und dem Mittelpunkt eines solchen Quadrats, die Hälfte des Überhangs, durch den der Teil unter dem Mittelpunkt der Welt den Teil überragt, der über dem Mittelpunkt der Welt ist.“302
2. suppositio:
„Wenn zwischen irgendwelchen Termen ein Verhältnis größerer Ungleichheit ist, und der größere [Term] ein Viertel des Überhangs verliert, durch den er den kleinere [Term] übertrifft, und der kleinere [Term] dasselbe Viertel genau genommen erwirbt, das von dem größeren [Term] verloren wird, [dann] wird das Verhältnis zwischen den gegebenen Termen mehr als bis zum durch 2 geteilten vermindert. Und folgerichtig verliert das Verhältnis oben seine Hälfte.“303
1. Korollar: „Unmittelbar nach dem Zeitpunkt, der gegenwärtig ist, wird irgendetwas aufsteigen, unmittelbar danach wird es absinken. Und dennoch wird nichts unmittelbar danach aufsteigen, das unmittelbar danach absinken wird.“304
2. Korollar: „Unmittelbar nach dem Zeitpunkt, der gegenwärtig ist, wird irgendetwas aufsteigen. Etwas wird gegenwärtig aufsteigen, das unmittelbar nach demselben Zeitpunkt absteigen wird. Und dennoch wird nicht unmittelbar nach dem Zeitpunkt, der gegenwärtig ist, irgendetwas absteigen, das unmittelbar nach demselben Zeitpunkt aufsteigen wird.“305
3. Korollar: „Unmittelbar nach dem Zeitpunkt, der gegenwärtig ist, wird irgendetwas aufsteigen, das unmittelbar nach demselben Zeitpunkt, der gegenwärtig ist, absteigen wird. Und dennoch wird nichts zugleich aufsteigen und absteigen, sobald man ,es‘ genau getrennt erfasst.“306
Am Ende des Kapitels 3.2.4 folgen die:
responsiones ad rationes ante oppositum:
Zur 1. ratio ante oppositum:
Alvarus Thomas kritisiert die Argumentation der 1. ratio, indem er die sequela verneint, deren Beweis als entgegen der propositio bezeichnet und bei dem Beispiel das Gegenteil behauptet.307
Es heißt weiter: „Denn jede der beiden Geschwindigkeiten muss bemessen werden. Mit der einen [Geschwindigkeit] wird Körper kreisförmig bewegt, und mit der anderen [Geschwindigkeit] wird er durch eine Bewegung der rarefactio zu dem Punkt von ihm bewegt, von dem die Geschwindigkeit der gesamten Bewegung abgelesen werden muss, wenn er stetig einen immer größeren Abstand vom Mittelpunkt erwirbt.“308 Es folgen darauf zwei Korollare:
1. Korollar: „Es ist möglich, dass irgendein Kreiskörper stetig gleichförmig kreisen und gleich schnell bewegt wird und dennoch stetig ausgedünnt und vergrößert wird.“309
2. Korollar: „Wenn irgendein Rad in einer Stunde kreisförmig bewegt wird, und der mittlere Punkt des Radius stetig mit einer Kreisbewegung gleichförmig bewegt wird, aber durch die Bewegung der rarefactio stetig seine Bewegung erhöht, es in einem beliebigen verhältnismäßigen Teil der Stunde, der folgt, um das Doppelte schneller als in dem unmittelbar vorhergehenden [Teil der Stunde] ausdünnt, dann ist der Raum, der von einem solchen Punkt beschrieben wurde, unendlich.“310
Zur 2. ratio ante oppositum:
Alvarus Thomas wendet sich gegen die Behauptungen der 2. ratio. Er sieht das Beispiel eher aus folgender Perspektive: „Vielmehr [sage ich] dagegen, dass die Bewegung des Schiffs für Sokrates ein Hindernis ist. Dennoch wird Sokrates nicht durch die Bewegung ermüdet, durch die er irgendeinen fixierten Raum beschreibt, sondern weil er irgendeinen nicht fixierten Raum beschreibt, bei dessen Beschreibung nicht folgt, dass Sokrates eine eigene Bewegung ausführt. Denn Sokrates wird an demselben fixierten Ort bleiben.“311
Zur 3. ratio ante oppositum:
Alvarus Thomas kann Teilen der 3. ratio zustimmen, andere verneint er, im Besonderen die sequela.
Korollar: „Irgendein Körper kann ungleichförmig in seinen Teilen so disponiert werden, dass er in begrenzter Zeit bewegt werden wird, bis sein Mittelpunkt der Mittelpunkt der Welt ist.“312
Weiterhin leitet er davon ab:
1. „Es ist deutlich, dass irgendein Raum ausreicht, um in der Hälfte einer Stunde mit der halben Geschwindigkeit durchquert zu werden, die mit dem Verhältnis F begann. Daher lege ich dar, das der zweite verhältnismäßige Teil des Teils D gemäß der Dimension vermindert wird, gemäß der er den Mittelpunkt der Welt durchquert, bis er gemäß der Dimension dem Raum gleich ist, von dem er begonnen wurde, von dem Verhältnis F in der Hälfte einer Stunde durchquert zu werden. Er bleibt dennoch immer so groß, wie er vorher war, so dass er gemäß einer anderen Dimension vermehrt wird. Und nachdem der zweite verhältnismäßige Teil des Teils D den Mittelpunkt der Welt gemäß sich und irgendeinem [Punkt] von sich durchquert wurde, zeichne ich ein Verhältnis aus, das G sei. Von ihm muss der vierte verhältnismäßige Teil absteigen, der kleiner als F ist, wie es fest steht.“313
2. „Und es ist deutlich, dass irgendein Raum ausreicht, im vierten Teil der Stunde mit einem halbierten Verhältnis durchquert zu werden. Also lege ich daher dar, dass der dritte verhältnismäßige Teil des Teils D gemäß der Dimension vermindert werde, gemäß der er den Mittelpunkt der Welt durchquert, bis er gemäß der Dimension dem Raum gleich ist, der Raum begonnen wurde, von dem Verhältnis G im vierten Teil der Stunde bewegt zu werden. Und so geschehe es bei einem beliebigen [Teil], der folgt: Er werde nämlich gemäß der Dimension vermindert, gemäß der er den Mittelpunkt der Welt durchquert, bis er dem Raum gleich ist, der begonnen wurde durchquert zu werden, [und zwar] in dem Verhältnis, von dem der unmittelbar folgende Teil beginnen muss, den Mittelpunkt der Welt zu durchqueren, und zwar in einer durch 2 geteilten Zeit oder einer kleineren [Zeit], als es die Zeit ist, in es der genau der unmittelbar vorhergehende Teil den Mittelpunkt der Welt durchquert. Dennoch bleibt der beliebige [Körper] stetig so groß, wie er vorher war. Daher wird er gemäß einer anderen Dimension vermehrt.“314
3. „Dann ist es deutlich, dass der gesamte Körper, nachdem der erste Teil des Teils D den Mittelpunkt der Welt hinter sich gelassen hatte, genau über eine Stunde hinweg oder über weniger Zeit hinweg bewegt werden wird, bevor der Mittelpunkt des Körpers der Mittelpunkt der Welt werde.“315
Das Kapitel wird damit abgeschlossen, dass Alvarus Thomas feststellt, in diesen Ausführungen Richard Swinesheads Beweis über dasselbe Thema im Kapitel über den Ort eines Elements kritisiert und verbessert zu haben.316
Fußnoten
Motus localis uniformis est, quo in aequalibus temporis aequalia spatia pertranseuntur rarefactione et condensatione deductis, deductis etiam aliis parvis quisquiliis, cuiusmodi est contra, mutatio spatii vel [id], quod non sit aliquod spatium, sufficit enim verum vel imagina[t]um spatium. Exemplum, ut si mobile in hora adaequate pertranseat leucam. Et in prima parte proportionali horae primam partem proportionalem leucae, in secunda secundam et sic consequenter. Thomas 1509, S. 126.
Motus vero difformis est, quando in aequalibus partibus temporis non aequalia spatia pertranseuntur ceteris paribus deductis deducendis, ut si mobile pertranseat in hora adaequate leucam, in prima medietate unam quartam et in secunda tres quartas, talis motus est difformis. Thomas 1509, S. 126.
Motus uniformiter difformis – ut communiter definitur – est triplex, quidam est uniformiter difformis quoad subiectum tantum, quidam quoad tempus tantum, quidam vero quoad subiectum et tempus similiter. Motus uniformiter difformis quoad subiectum – ut communiter definitur – est, quando cuiuscumque partis subiecti dimidium tantum exceditur in velocitate ab extremo velociori illius, quantum excedit extremum tardius motum in velocitate. Exemplum ut motus rotae figuli, et per dimidium intelligas punctum in medio vel [eum], qui imaginarie est, ibi termin[]ando. Motus vero uniformiter difformis quoad tempus est, quando cuiuscumque partis acceptae secundum tempus, in qua adaequate est in aliqua parte temporis gradus medius, qui est in medio talis partis, tanto excedit extremum remissius, quanto exceditur ab intensiori. Exemplum, ut si aliquod mobile incipiat moveri a non gradu continuo intendendo uniformiter motum suum per aliquod tempus, tunc talis motus est uniformiter difformis quoad tempus. Motus autem uniformiter difformis quoad tempus et quoad subiectum definitur coniungendo definitiones motus uniformiter difformis quoad tempus et quoad subiectum. Thomas 1509, S. 126.
Motus autem difformiter difformis consimiliter dividi potest, videlicet motuum difformiter difformium, alius est difformiter difformis quoad tempus, alius quoad subiectum, alius quoad tempus et subiectum simul. Thomas 1509, S. 126.
[...] si esset aliquis motus uniformiter difformis quoad subiectum, maxime esset motus rotae, quo movetur circulariter, sed talis motus non est uniformiter difformis quoad subiectum, igitur consequentia patet cum maiore, et arguitur minor, quia si talis motus est uniformiter difformis, capio unam rotam, quae moveatur uniformiter difformiter a non gradu in centro usque ad octavum in circumferentia, et arguo sic: talis motus per te est uniformiter difformis a non gradu usque ad octavum, ergo velocitas eius correspondet gradui medio, puta ut 4, qui medius gradus ut 4 est in puncto medio talis rotae, sed consequens est falsum, igitur illud, ex quo sequitur, consequentia patet supposita opinione tenente motum uniformiter difformem correspondere motui existenti in medio corporis mobilis. Thomas 1509, S. 127.
Dices forte et bene negando antecedens et ad probationem concedendo maiorem et negando minorem, et cum probatur, admitto casum cum his, quae ibi supponuntur, et concedo antecedens et consequentiam et distinguo consequens quantum ad illam particulam, in qua dicitur, quod talis gradus medius est in puncto existenti in medio talis rotae, quia aut tu intelligis de medio magnitudinis illius rotae, quod quidem medium est in medio inter centrum et circumferentiam talis rotae dividendo illam rotam in duas rotas concentricas aequalis magnitudinis, quamvis sint inaequal[e]s ambitus et circumferentiae, ut patet in figura, et sic nego, aut loqueris de puncto existente in medio longitudinis inter centrum et circumferetiam, et sic bene concedo, quod ibi est gradus medius, ut bene probat argumentum. Thomas 1509, S. 127.
Unde dico, quod quamvis in qualitate uniformiter difformi medius gradus debeat esse in medio corporis quantum ad magnitudinem, in motu tamen uniformiter difformi non oportet, quod gradus medius sit in medio corporis quantum ad magnitudinem, sed oportet, quod sit in medio corporis quantum ad longitudinem (sumendo longitudinem eius a puncto non moto sive tardissime moto usque ad punctum velocissime motum), quia secundum illum modum praecedit ille motus uniformiter difformis. Thomas 1509, S. 127.
[...] aliqua pars illius rotae non movetur uniformiter difformiter, ergo sequitur, quod ipsa tota rota non movetur uniformiter difformiter. Thomas 1509, S. 127.
[...] oportet, quod in motu uniformiter difformi cuiuslibet partis gradus medius, (id est, qui est in medio longitudinis, ut dictum est,) tantum excedat infimum, quantum exceditur a summo, (ut patet ex definitione). Thomas 1509, S. 127.
Sed contra, quia utraque medietas illius quadrati ABCD movetur velocius quam ut 4, ergo sequitur, quod totum illud quadratum movetur velocius quam ut 4, consequentia patet, quia totius velocitas conficitur ex partium velocitatibus, et velocitatis denominatio ex utriusque medietatis denominationibus constatur. Thomas 1509, S. 127.
[...] cuiuslibet motus uniformiter difformis gradus velocissimus [], quo movetur punctus velocissime motus, tantum excedit gradum medium, quantum gradus medius excedit gradum, quo movetur punctus tardissime, motus, ut concedit haec opinio et communis sc[h]ola, sed motus talis quadrati ABCD non est huiusmodi, igitur talis motus non est uniformiter difformis. Thomas 1509, S. 128.
[...] si motus talis rotae esset uniformiter difformis a non gradum usque ad octavum, sequeretur, quod adaequata velocitas illius rotae esset ut quatuor, sed consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 128.
Sed iam probo, quod totius rotae ad minorem circulum ei concentricum sit proportio quadrupla, quia – ut demonstrat Bravardinus in tractatu proportionum capite quarto – semper inter duos circulos inaequales est duplicata proportio ad proportionem, quae est inter diametros eorundem circulorum, ita quod proportio circulorum est proportio diametrorum duplicata, ut etiam facile potest intueri in figura supposita, sed diametri totius rotae ad diametrum circuli DEF est proportio dupla, ergo totius rotae ad circulum DEF est proportio quadrupla, quae est dupla ad duplam. Quod fuit probandum. Thomas 1509, S. 128.
Et sic ex hac deductione patet, quod totus ille motus est ut quinque, quia illae tres quartae denominant ut quatuor cum dimidio, et alia quarta, quod est minor circulus, denominat ut dimidium, (cum sit ut duo), igitur totus motus est ut quinque et sic non est adaequate ut quatuor. Quod fuit probandum. Thomas 1509, S. 128.
[...] si illa definitio esset bona, sequeretur, quod motus caeli non esset uniformiter difformis quoad subiectum, sed consequens est falsum, et contra communiter opinantes. Thomas 1509, S. 128.
[...] si esset aliquis motus uniformiter difformis quoad subiectum, maxime esset motus localis, quo per rarefactionem movetur unum quadratum, quod rarefit uniformiter a non gradu in extremo quiescente usque ad octavum in altero extremo, sed haec non, igitur. Thomas 1509, S. 128.
[...] motus uniformiter difformis quoad subiectum non bene definitur isto modo: motus uniformiter difformis quoad subiectum est, cuius omnes partes immediatae secundum extensionem sunt immediatae secundum intensionem motus sive velocitatum, ita quod remississimus gradus velocitatis, qui est in intensiori, sit remississimus, qui non est in remissiori illarum duarum partium sibi immediatarum. Thomas 1509, S. 128.
[...] motus uniformiter difformis quoad subiectum non bene definitur isto modo: motus uniformiter difformis quoad subiectum est, quando cuiuscumque partis subiecti punctus, qui est in medio, (loquor de puncto vero vel imaginario) tanto exceditur in velocitate ab extremo illius partis velocissime moto, quantum excedit extremum remississime motum eiusdem partis sive non motum, (quod dico propter motum terminatum ad non gradum.) Thomas 1509, S. 129.
[...] motus uniformiter difformis quoad subiectum non bene definitur sic: motus uniformiter difformis quoad subiectum est, quando cuiuscumque partis subiecti dimidium sive punctus, qui est in medio talis partis, (in medio inquam secundum longitudinem) tantum exceditur in velocitate a puncto sive ab extremo velocissime moto, quantum excedit punctum sive extremum tardissime motum in velocitate sive extremum non motum (quod dico propter motum terminatum ad non gradum). Thomas 1509, S. 129.
[...] motus uniformiter difformis quoad subiectum – ut pro nunc mihi apparet – bene definitur sic: motus uniformiter difformis quoad subiectum est, quando quilibet punctus subiecti intrinsecus et etiam extrinsecus velocissime motus in ea proportione velocius movetur, in qua magis distat a centro talis motus. Thomas 1509, S. 129.
[...] cuiuslibet, quod uniformiter difformiter movetur quoad subiectum, quaelibet pars quantitiva uniformiter difformiter movetur quoad subiectum. Thomas 1509, S. 129.
[...] non oportet, quod motus uniformiter difformis quoad subiectum correspondeat gradui motus existenti in medio magnitudinis talis corporis, nec in medio longitudinis. Thomas 1509, S. 129.
[...] motus uniformiter difformis quoad subiectum commensurari habet penes gradum medium inter summ[um] et infimum vel non gradum, ubicumque sit talis gradus. Patet, quia non videtur alius modus cognoscendi totalem velocitatem motus uniformiter difformis quoad subiectum. Thomas 1509, S. 129.
Definitio illa, quae communiter datur de motu uniformiter difformi quoad subiectum, non est sufficienter assignata, quoniam nec valet, si intelligatur de medio magnitudinis, nec [valet], si intelligatur de medio longitudinis, ut declaratum est in secundo correlario. Thomas 1509, S. 129.
Quia tamen in primo argumento quaeritur, an in motu uniformiter difformi quoad subiectum gradus medius debeat esse in medio corporis quoad magnitudinem vel quoad longitudinem, dico, quod neuter illorum {modorum} requiritur, quod sit in medio corporis, ut dicit secundum correlarium. Thomas 1509, S. 129.
Quia tamen inquirit[ur], penes quem punctum debeat ibi attendi motus illius quadrati, dico, quod debet attendi penes punctum, qui movetur gradu medio inter gradum octavum, quo movetur punctus velocissime motus, illius partis et gradum, quo movetur punctus tardissime motus, eiusdem quadrati, ubicumque talis punctus fuerit, de situ enim eius non est curandum. Thomas 1509, S. 130.
Ad secundum argumentum cum sua confirmatione dico, quod sunt pro conclusione resp[o]nsiva, quia impugnant definitionem communem. Dico tamen, quod motus caeli est uniformiter difformis, ut postea dicetur, quia quodlibet punctum eius in ea proportione, in qua plus distat a polo proximiori vel aeque propinquo, in ea velocius movetur. Thomas 1509, S. 130.
Prima opinio est Guillermi Hentisberi, qui dicit, quod velocitas motus uniformiter difformis quoad subiectum debet attendi penes punctum velocissime motum. Thomas 1509, S. 130.
[...] quod motus uniformiter difformis quoad tempus debet attendi penes gradum medium quoad tempus, id est penes gradum, quo movetur mobile in medio talis temporis, et motus uniformiter difformis quoad subiectum debet attendi penes gradum medium totius latitudinis uniformiter difformis. Thomas 1509, S. 130.
Advertendum tamen, quod quando dicimus, quod velocitas motus uniformiter difformis debet attendi penes gradum mediuum voluminis, dicere, quod tale mobile uniformiter difformiter motum movetur adaequate ita velociter, sicut movetur punctus, in quo est gradus medius talis latitudinis. Et quando dicitur, quod motus uniformiter difformis quoad tempus velocitas debet attendi penes gradum medium, qui est in medio temporis, volumus dicere, quod tam velociter movetur in illo tempore adaequate illud mobile, ac si per totum illud tempus moveretur illo gradu, quem habet in medio illius temporis. Thomas 1509, S. 130.
Advertendum est ulterius, quod velocitas motus quoad effectum debet attendi penes spatium pertransitum, ita quod quanto spatium pertransitum fuerit maius in aequali tempore, tanto motus erit velocior. Thomas 1509, S. 130.
Dico tamen, quod non debet attendi velocitas motus localis penes spatium corporale nec penes spatium superficiale, sed penes spatium lineale descriptum a certo puncto, quia tunc si unus equus traheret duas trabes inaequales aeque velociter, tamen sequeretur, quod maior velocius moveretur, cum describat maius spatium corporale et superficiale quam minor, quod tamen falsum, quia aequaliter moventur, cum in utraque punctus medius aequale spatium describat. Thomas 1509, S. 130.
Et sic etiam dicendum est de motu circulari uniformiter difformi quoad subiectum, quod velocitas eius habet attendi penes lineam circularem descriptam a puncto, in quo est gradus medius illius latitudinis motus uniformiter difformis. Thomas 1509, S. 130.
Velocitas motus uniformiter difformis quoad tempus et quoad subiectum debet attendi penes lineam descriptam a puncto, in quo est medius gradus talis latitudinis. Thomas 1509, S. 130.
Et similiter dicendum est de motu difformiter difformi quoad tempus, quod velocitas eius debet attendi penes spatium pertransitum in tali tempore. Thomas 1509, S. 130.
Ex his tamen infertur istam consequentiam non valere. Ista rota uniformiter difformiter mota quoad subiectum describit maiorem lineam quam punctus, in quo est gradus medius totius latitudinis motus, igitur movetur velocius quam ille punctus, quia antecedens est verum, cum punctus existens in circumferentia sive peripheria ipsius rotae describat maiorem lineam quam punctus, in quo est gradus medius latitudinis motus, et utraque illarum linearum per motum rotae describitur. Thomas 1509, S. 130.
Secundo sequitur, quod ista consequentia non valet: ista rota uniformiter difformiter movetur quoad subiectum et citius transibit lineam circularem aequalem lineae descriptae a puncto, in quo est medius gradus latitudinis, quam talis punctus, in quo est gradus medius latitudinis motus, describat suam lineam, ergo rota citius movetur quam talis punctus. Thomas 1509, S. 130.
[...] ista consequ[e]ntia non valet, istud lignum maius spatium pertransibit quam illud in eodem tempore, igitur velocius movebitur in eodem tempore. Thomas 1509, S. 130.
[...] quaeritur, penes quid tamquam penes effectum motus difformis quod ad subiectum velocitas attendi habeat, an videlicet penes lineam descriptam a puncto velocissime moto, an penes lineam descriptam a puncto, in quo est gradus medius, an penes reductionem ad uniformitatem. Thomas 1509, S. 131.
Et arguitur primo, quod non debeat attendi penes primum, ut opinatur hentisber in tractatu de motu locali capite primo, quia si, sic sequeretur pari ratione, quod deberet attendi penes punctum tardissime motum, sed hoc est falsum cum aliquando non detur, igitur. Thomas 1509, S. 131.
[...] plerumque non datur punctus tardissime motus, et ideo non poterit continuo velocitas motus penes talem punctum attendi. Thomas 1509, S. 131.
Sed contra, quia etiam – ut inferius videbitur – datur aliquis motus difformis quoad subiectum, cuius non datur punctus continuo velocissime motus, ut patebit in rota rarefiente, igitur etiam non potest continuo attendi penes talem punctum, et si talis punctus continuo maneat, non tamen linea, quam discribit adaequate. Thomas 1509, S. 131.
[...] tunc sequeretur, quod rota uniformiter difformiter mota moveretur continuo ita velociter sicut medietas eius, quae velocius movetur, sed hoc est falsum. Thomas 1509, S. 131.
Sed contra, quia plerumque non datur punctus extremus ut posito, quod deus corrumpat in rota omnia puncta extrema. Item etiam nominalisando non datur punctum extremum, quia termin[a]ta omnia talia indivisibilia negat, et figmentum reputat, igitur saltem secundum viam nominalium non potest sumi velocitas motus difformis quoad subiectum penes lineam a puncto velocissime moto descriptam. Dices, quod in tali casu velocitas illius motus debet attendi penes lineam descriptam a puncto imaginario posito in peripheria, hoc est, tota rota tantam lineam describit et tam velociter {movetur, quam velociter movetur unus punctum, qui esset in peripheria talis rotae.} Thomas 1509, S. 131.
Sed contra capio unam rotam, quae difformiter movetur quoad subiectum, et cum incipit moveri, incipiat maiorari per rarefactionem, ita quod punctus eius extremus continuo magis ac m[a]gis distat a centro, ita quod in principio totius rotae diameter sit pedalis et in fine bipedalis. Thomas 1509, S. 131.
[...] velocitas talis motus non potest attendi penes lineam descriptam a puncto velocissime moto. Thomas 1509, S. 131.
[...] talis punctus nullam lineam describit, quod probatur sic, quia nullam circularem, ut notum est, cum non redeat ad idem punctum, a quo recessit, sed ad punctum in duplo magis distans a centro, nec etiam lineam rectam aliquam describit et non videtur, quam aliam lineam describat, igitur non datur ibi linea descripta a tali p[u]ncto, penes quam possit velocitas motus illius rotae commensurari. Thomas 1509, S. 131.
[...] qua illa rota non movetur ita velociter, sicut punctus eius extremus movetur in principio motus, ut notum est, cum maiorem lineam describat per totum tempus, quam si rota maneret invariata quoad magnitudinem, nec tanta velocitate, quanta movetur in fine motus, nec in medio instanti motus, quia tunc hoc esset coincidere cum alia opinione, quae commensurat penes gradum medium, igitur non videtur, penes quid attendi habeat velocitas talis motus. Et sic habetur, quod non omnis velocitas motus difformis quoad subiectum attendi habeat penes velocitatem puncti velocissime moti. Thomas 1509, S. 131.
[...] si illud esset verum, sequeretur haec conclusio, quod aliquod mobile continuo uniformiter moveretur, et tamen quilibet punctus eius intrinsecus continuo intenderet motum suum, sed hoc videtur impossibile. Thomas 1509, S. 131.
Contra, quia tunc pari pacto sequeretur, quod aliquod mobile continuo uniformiter moveretur, et tamen quilibet punctus eius intrinsecus continuo remitteret motum suum, sed hoc videtur inconveniens. Thomas 1509, S. 131.
Contra, quia tunc sequeretur, quod a qualibet parte proportionali alicuius mobilis secundum certam divisionem procedendo demeretur aliqua velocitas, ita quod quaelibet secundum talem divisionem moveatur minori velocitate, quam antea movebatur, et tamen totum mobile movetur continuo uniformiter et aeque velociter sicut antea, sed consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 132.
[...] si illud esset verum, sequeretur, quod si una rota moveretur difformiter quoad subiectum a non gradu usque ad certum gradum, ita quod pars illa, quae est a centro usque ad medietatem semidiametri, moveatur a non gradu usque ad quartum, et residua pars usque ad circumferentiam moveatur a quarto usque ad duodecimum, tunc talis rota moveretur velocitate ut sex, sed consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 132.
Sed contra, quia si in omni motu uniformiter difformi quoad subiectum debeat velocitas attendi penes gradum medium, vel igitur per gradum medium intelligitur gradus, qui est medio talis subiecti quoad magnitudinem vel in medio quoad longitudinem vel in medio quoad magnitudinem et longitudinem simul, sed nullum istorum est dicendum, igitur non debet motus uniformiter difformis quoad subiectum velocitas penes gradum medium commensurari et attendi. Thomas 1509, S. 132.
[...] si illa pars esset vera, sequeretur, quod caelum non movetur ita velociter sicut linea aequinoctialis (et loquor de primo mobili), sed consequens est falsum, igitur et antecedens. Thomas 1509, S. 133.
Consequentia patet, et coloratur falsitas consequentis, quia si non movetur ita velociter sicut linea aequinoctialis, et linea aequinoctialis est linea existens in medio eius, ergo mobile motum uniformiter difformiter quoad subiectum non movetur ita velociter sicut punctus existens in medio eius. Thomas 1509, S. 133.
Sed contra, quia vel debet attendi penes lineam descriptam a puncto medio in superficie concava vel in superficie convexa, sed nullum istorum est dicendum, igitur. Thomas 1509, S. 133.
[...] punctus existens in medio quantum ad superficiem convexam non est simpliciter in medio nec punctus existens in superficie concava, igitur. Item tale mobile non movetur ita velotiter sicut superficies convexa nec ita tarde sicut superficies concava, ergo sequitur, quod velocitas eius non habet attendi penes punctum, hoc est penes lineam descriptam a puncto existente in superficie convexa nec in superficie concava. Thomas 1509, S. 133.
Dices, quod velocitas illius primi mobilis mensuranda est a puncto existente in medio inter superficiem concavam et convexam inter polum et punctum velocissime motum totius orbis. Thomas 1509, S. 133.
[...] quia tunc sequeretur haec conclusio, quod si primum mobile condensaretur versus superficiem convexam quiescentem, ipsum continuo velocius et velocius moveretur, et si rarefieret versus concavam quiescente etiam convexa, ipsum mobile continuo tardius et tardius moveretur, sed consequens est falsum, quia tunc sequeretur, quod quantocumque illud mobile efficeretur maius, tardius moveretur, et quanto minus, velocius, quod videtur absurdum. Thomas 1509, S. 133.
[...] quia tunc sequeretur, quod si omnes sphaerae intermediae corrumperentur, et primum mobile quiescente convexa superficie rarefieret versus axem, quoad usque ex orbe efficiatur sphaera solida unicam superficiem dumtaxat habens, tunc illud mobile iam fact[a] sphaera solida longe tardius moveretur quam antea, et etiam moveretur uniformiter difformiter quoad subiectum, sed consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 133.
[...] si illa opinio esset vera, sequeretur, quod si aliqua rota continuo condensaretur versus centrum movente etiam superficie convexa et motore non movente a maiori conamine, tunc continuo illa rota tardius et tardius moveretur, sed consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 133.
Item haec circuitio est ita velox sicut antea, et haec circuitio est hic mot[o]r circularis, igitur hic motus circularis est ita velox sicut antea, et per consequens illa rota tunc non tardius movetur. Thomas 1509, S. 133.
[...] quia si illa solutio esset bona, sequeretur, quod ab eadem proportione potentiae ad suam resistentiam provenirent inaequales motus et aequales circuitiones, quod est falsum. Thomas 1509, S. 134.
[...] quia hoc dato iam destruitur fundamentum totius materiae, et iam pari facilitate protervus physicus concederet, quod a proportione dupla et a proportione quadrupla aequales velocitates natae sunt provenire, et multa similia, quae sunt absona calculatori philosopho. Thomas 1509, S. 134.
[...] magnitudo rotae tenet se ex parte potentiae. Modo manente eodem conamine potentiae rota tardius movetur et a minore proportione, quia antea magnitudo ip[s]ius rotae iuvabat potentiam ad describendam lineam. Modo vero cum ipsa rota continuo efficiatur minor, non ita iuvat potentiam sicut ante. Thomas 1509, S. 134.
Manifestum est enim, quod si in superficie alicuius rotae addatur aliquid eiusdem speciei continuatum cum rota nullius gravitatis, et Socrates giret totum illud ab eodem conamine, illa totalis rota velocius movetur, quam movebatur antea pars eius, et tamen potentia manet aequalis, et resistentia rotae, sed totalis proportio est maior, quia iuvatur ibi potentia Socratis a magnitudine rotae. Thomas 1509, S. 134.
[...] quia magnitudo tenet se ex parte resistentiae, ergo non ex parte potentiae etiam manente aequali gravitate omnino. Probatur antecedens de orbe, qui maioratur per rarefactionem, quousque fiat spera solida, qui tunc tardius movetur, quam quando erat minor, ut patet ex secunda replica huius quarti argumenti. Dices sicut dicendum est, quod nec magnitudo, nec parvitas in talibus tenet se ex parte potentiae ut satis probat replica, sed distantia puncti a centro, penes cuius motum debet attendi velocitas totius mobilis, puta ipsius puncti, in quo est gradus medius, totius latitudinis motus tenet se ex parte potentiae. Thomas 1509, S. 134.
Ceteris enim paribus iuvat potentiam ad velocius describendum lineam, quam describit, quando recedit a centro, et per contrarium iuvat ad describendam tardius, quando magis accedit ad centrum, a quo exoritur motus. Et sic dico, quod quando rota rarefit versus circumferentiam movente circumferentia, tota proportio efficitur maior, et quando condensatur ordine converso, tota proportio efficitur minor. Thomas 1509, S. 134.
[...] quia ista solutio non satisfacit adhuc, enim sequitur, quod ab inaequalibus proportionibus aequales circuitiones proveniunt, quod est impossibile. Thomas 1509, S. 134.
[...] aliquis motus est uniformiter difformis quoad subiectum, et tamen eius velocitas non correspondet gradui medio. Thomas 1509, S. 134.
[...] suppono, quod rarefactio sit motus localis difformis quoad subiectum. Quo supposito pono, quod sint duo pedalia secundum omnem dimensionem, puta A, B, et volo, quod a rarefiat uniformiter, quousque efficiatur in duplo longius et in duplo latius uniformiter, et B rarefiat uniformiter, quousque efficiatur in sesquialtero longius et in sesquialtero latius uniformiter, ita quod A in fine sit unum quadratum, cuius costa sit dupla ad costam eiusdem in principio rarefactionis, et B sit aliud quadratum, cuius costa in fine rarefactionis sit sesquialtera ad costam eius in principio rarefactionis. Quo posito sic arguitur: si ill[i] motus, quo movetur A, et etiam, quo movetur B, debeant commensurari penes punctum medium, sequitur, quod A adaequate in duplo velocius moveretur quam B, sed consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 134.
[...] contra tertiam partem quaestionis videlicet, quod debet attendi motus localis difformis velocitas quoad subiectum penes reductionem ad uniformitatem. Thomas 1509, S. 134.
[...] motus circularis in subiecto circulari non potest reduci ad uniformitatem, igitur non debet attendi penes reductionem ad uniformitatem. Thomas 1509, S. 134.
[...] si reduceretur ad uniformitatem motus circularis alicuius rotae a non gradu usque ad octavum, vel oporteret reducendo ab aliqua parte capere aliquam certam velocitatem et ponere in aequali parte, sicut fit in reductione qualitatis uniformiter difformis, vel capiendo ab aliqua parte et ponendo in minori vel a minori et ponendo in maiori. Thomas 1509, S. 135.
Non tertium, quia tunc facile reducendo ad uniformitatem probaretur, quod velocitas illius rotae sit infinita, quia caperetur a prima parte proportionali unus gradus, et a secunda tantum, et a tertia tantum, et poneretur per totam rotam, et sic esset infinita velocitas. Nec secundum, quia tunc sequeretur, quod tota velocitas esset minor quam ut quatuor, ut si velocitas totius rotae poneretur immedietate eius, et ibi esset uniformis ut quatuor, deinde accipiendo medietatem illius latitudinis motus reducta ad uniformitatem, puta duos gradus, et ponendo eos in alia medietate et sic tota velocitas maneret ut duo. Nec est dicendum primum, quia divisa illa rota in duas partes concentricas, quarum una sit quarta pars totius rotae, et residua versus circumferentiam sit tres quartae, ut ponebatur in praecedenti capite in secunda confirmatione, puta ultima primi argumenti. Thomas 1509, S. 135.
Respondeo alter, quod de facto motus difformis quoad subiectum velocitas nequaquam commensurari debet per reductionem ad uniformitatem, sed commensuranda est penes denominationem partium non quantum ad magnitudinem, sed quantum ad longitudinem. Volo dicere, quod non in ea proportione[], qua pars est maior altera, in ea propor[ti]one velocitas motus existens in ea plus facit ad denominationem totius velocitatis. Sed volo dicere, quod in ea proportione, in qua est longior ceteris paribus, in ea plus facit ad denominationem totius, ita quod tantum adaequate movetur una rota, quantum una linea procedens a centro illius rotae usque ad circumferentiam. Et si talis linea moveatur a non gradu usque ad octavum, etiam tota rota. Thomas 1509, S. 135.
[...] si talis modus cognoscendi velocitatem motus difformis quoa[d] subiectum esset videlicet validus, sequeretur, quod dabilis esset una pars rotae uniformiter difformiter motae, quae non uniformiter difformiter moveretur, immo non esset dabilis gradus, quo adaequate moveretur, sed quolibet inadaequate citra summum, et consequens omni opinioni adversatur, igitur illud, ex quo sequitur. Thomas 1509, S. 135.
In oppositum tamen est communis schola asserens velocitatem motus difformis quoad subiectum aliquo illorum modorum attendi debere sive commensurari. Thomas 1509, S. 135.
Vgl. Thomas 1509, S. 135.
Vgl. Thomas 1509, S. 135.
[...] quod in motu circulari duo consideranda sunt, puta ipsa circuitio, et ipse motus circularis, quamvis enim idem sit motus circularis et circuitio, penes aliud tamen commensurari habet velocitas circuitionis, et velocitas motus circularis, sicut idem est albedo et similitudo, et penes aliud cognosci habet intensio albedinis, et intensio similitudinis, quod facile ex dialecticis percipi potest. Thomas 1509, S. 135.
Velocitas enim motus circularis attenditur penes lineam descriptam a certo puncto. Thomas 1509, S. 135.
Sed velocitas circuitionis attendi habet penes angulum descriptum in tanto vel tanto tempore circa centrum, ita quod si in aequali tempore duo mobilia sive aequalia sive inaequalia circulariter mota aequales angulos circa centrum describunt, ipsa aequaliter circueunt et circumgirant. Si vero in eodem tempore inaequales describant circa centrum angulos, notum evadet eorum circuitiones inaequales esse. Thomas 1509, S. 135.
Vgl. Thomas 1509, S. 135.
Posset tamen facile attendi velocitas circuitionis penes velocitatem motus alicuius puncti aequaliter distantis a centro, hoc est dicere, quod si in duobus mobilibus circulariter – sive aequalia sint, sive inaequalia – duo puncta aequaliter distantia a centro aequaliter moveantur, talia mobilia aequaliter circueunt. Thomas 1509, S. 135.
Non tamen arbitreris, quod quanto punctum est propinquius centro, tanto velocius circuit, quam quodlibet aequevelociter circuit cum altero, dummodo corporis motus sit uniformiter difformis quoad subiectum. Quare perspicuum est videre distantiam punctorum nullo pacto conferre ad velocitatem circuitionis, (loquor de distantia a centro), quamvis plurimum ad velocitatem motus circularis. Thomas 1509, S. 135.
[...] velocitas motus uniformiter difformis quoad subiectum non debet attendi aut commensurari penes velocitatem puncti existentis in medio corporis quantum ad magnitudinem. Thomas 1509, S. 135.
[...] velocitas motus uni[for]miter difformis quoad subiectum non debet attendi penes velocitatem puncti existentis in medio mobilis quantum ad longitudinem. Thomas 1509, S. 135f.
[...] velocitas motus uniformiter difformis quoad subiectum commensurari debet penes gradum medium totius latitudinis talis motus uniformiter difformis, ubicumque fuerit talis gradus, sive in medio corporis quantum ad magnitudinem, sive non. (Non est cura.) Thomas 1509, S. 136.
[...] velocitas motus difformiter difformis quoad subiectum cognosci potest penes denominationem partium quantum ad longitudinem. Thomas 1509, S. 136.
[...] probabile est velocitatem motus difformis quoad subiectum attendi debere penes gradum summum. Thomas 1509, S. 136.
[...] distantia punctorum a centro, a quo procedit motus difformis quoad subiectum, tenet se ex parte potentiae, et auget proportionem potentiae ad resistentiam, necnon eidem potentiae est adiumento, et per oppositum propinquitas, nec magnitudo aut parvita[]s aliquid facit. Thomas 1509, S. 136.
[...] non stat aliquam rotam, quae movetur a virtute Socratis ut quatuor, rarefieri et maiorari per continuam elongationem punctorum a centro et ipsam continuo ab eadem proportione moveri ceteris paribus. Thomas 1509, S. 136.
[...] propinquitas aut distantia punctorum a centro nihil conducit ceteris paribus ad velocitatem circumgirationis sive circuitionis, quod idem est. Thomas 1509, S. 136.
[...] numquam concendendum est ab aequalibus proportionibus inaequales motus circulares provenire aut ab inaequalibus proportionibus aequales circuitiones, ut solutio quarti argumenti ostendit. Thomas 1509, S. 136.
[...] si in eodem axe ponantur infinitae rotae continuo minores et minores, ita quod diametri primae sit dupla ad diametrum secundae et secundae ad diametrum tertiae et sic consequenter, et Socrates moveat omnes illas rotas mediante illo axe, in infinitum tarde movetur ibi aliqua rota, nihilominus tamen quaelibet rota ita velociter circuit sicut prima. Thomas 1509, S. 136.
[...] in casu praedicto non ab eadem proportione adaequate Socrates movet primam rotam et secundam, sed a maiori primam quam secundam, quia distantia punctorum mediorum est adiumento potentiae Socratis. Thomas 1509, S. 136.
[...] si sunt duae quantitates aequalis profunditatis uniformiter et aeque late uniformiter, et una longior al[t]era, in quacumque proportione est longior, in eadem est maior. Thomas 1509, S. 136.
[...] si duae quantitates inaequales sint aeque profunde uniformiter et aeque longe uniformiter, et una latior altera, in quacumque proportione una est latior, in eadem est maior. Thomas 1509, S. 136.
[...] si sint duae quantitates aeque longe aeque late uniformiter, et una sit in aliqua pro[p]ortione profundior altera, in eadem proportione, in qua est profundior, est maior. Thomas 1509, S. 136.
[...] proportio quadratorum perfectorum et aeque profundorum uniformiter est proprortio costarum duplicata. Et voco quadratum perfectum, cuius omnes costae sunt aequales, et omnes anguli recti aequales. Non intelligas tamen, quod velim dicere, quod omnes costae debent esse aequales secundum omnem dimensionem, sed satis est secundum latitudinem et longitudinem. Thomas 1509, S. 137.
[...] proportio duorum corporum cuborum sive perfecte quadratorum simpliciter, cuiusmodi sunt data sive taxilli, quorum longitudo est aequalis latitudini et profunditati, est proportio costarum triplicata. Thomas 1509, S. 137.
[...] datis duobus quadrangulis cubis, quorum costae se habent in proportione sesquialtera, maioris quadranguli ad minorem est proportio tripla supertripartiens octavas, qualis 27 ad 8. Thomas 1509, S. 137.
[...] datis duobus quadratis cubicis, quorum latera se habent in proportione tripla, inter maius et minus reperitur proportio vicecupla septupla, qualis est proportio 27 ad unum. Thomas 1509, S. 137.
[...] secundum opinionem, quae ponit velocitatem motus difformiter difformis quoad subiectum attendi debere penes gradum summum, proportio motus duarum sp[h]aerarum sive duorum orbium pariterque duorum circulorum in aequali tempore ceteris paribus circumgiratorum est sicut proportio suorum diametrorum. Thomas 1509, S. 137.
[...] proportio motuum duarum sphaerarum solidarum est sicut proportio diametrorum. Thomas 1509, S. 137.
Sed quantum ad aliam opinionem patet, quam secundum aliam velocitas sp[h]aerae solidae debet attendi secundum lineam descriptam a puncto medio semidiametri inter centrum et circumferentiam, et per consequens a puncto descripto ab una quarta semidiametri, sed in quacumque proportione una diameter est maior altera, in eadem una quarta est maior una quarta alterius, ergo secundum hanc opinionem in quacumque proportionem diameter unius sp[h]aerae solidae erit maior diametro alterius, in eadem proportione maiorem lineam describet punctus medius semidiametri, et per consequens proportio motus erit sicut proportio diametrorum. Thomas 1509, S. 137.
[...] proportio motuum duarum sp[h]aerarum inaequalium in eode[m] tempore circumgiratarum, dummodo sint solidae, est subtripla ad proportionem sp[h]aerarum inter se. Thomas 1509, S. 137.
[...] si una sp[h]aera est in octuplo maior altera, quae movetur praecise in duplo velocius altera, et si una sp[h]aera fuerit in triplo supertripartienti octavas maior altera, ipsa movetur in sesquialtero velocius altera. Thomas 1509, S. 137.
[...] quemadmodum probabile est velocitatem motus, de quo est praesens inquisitio, attendi debere penes lineam descriptam a puncto, in quo est gradus medius, aut penes reductionem ad uniformitatem denominationis, ita probile est talem motum attendi debere penes lineam a puncto velocissime moto descriptam, sive talis punctus velocissime motus sit verus sive imaginarius. Thomas 1509, S. 138.
[...] utramque opinionem sustinemus opere praetium est omnes illas rationes solvere, quamvis illae, quae sunt contra unam opinione[m], sint pro altera. Thomas 1509, S. 138.
[...] velocitas motus difformis quoad subiectum attendi debet penes punctum velocissime motum. Thomas 1509, S. 138.
[...] ad replicam respondeo, quod quamvis non detur aliquando punctus, qui velocissime movetur, verus, datur tamen imaginarius, quod sufficit, et similiter non detur linea vera, datur tamen imaginaria, quam describit, et loquor in proposito de vero vel imaginario, ut ad propositum conducit. Thomas 1509, S. 138.
Et ad secundam replicam, quae ponit rotam continuo rarefieri, ita quod continuo magis distent puncta extra a centr[u]m, admitto casum et nego antecedens et ad probationem nego, quod nullam lineam describat, et cum probatur, quia nec rectam nec circularem, concedo antecedens et nego consequentiam. Multae enim lineae sunt, quae nec rectae nec circulares sunt, ut patet de linea pro media parte recta et pro media circulari. Hoc idem patet de linea girativa et de filio ad globum redacto. Et ideo dico, quod talis linea habet se quasi ad modum lineae girativae vel curvae. Thomas 1509, S. 138.
Ad secundam confirmationem dico breviter, quod talis rota movetur ita velociter, sicut punctus, eius extremus, movetur in toto tempore adaequate. Et si quaeras, cui correspondet velocitas illius puncti in toto illo tempore adaequate: Respondeo, ut mihi videtur pro nunc, quod correspondet velocitati, quam talis punctus habet in instanti medio totius temporis. Thomas 1509, S. 138.
[...] quod stabit punctum extremum moveri ita velociter, sicut antea movebatur qualibet parte proportionali carente velocitate sive quiescente. Thomas 1509, S. 138.
Sed dico, quod cum aliqua pars proportionalis devenerit ad non gradum velocitatis, tota rota quiescit. Utrum autem posset fieri, quod in calce argumenti ponitur videlicet, quod a qualibet per parte propotionali secundum certam divisionem dematur medietas velocitatis absque hoc, quod dematur aliquid a puncto existente in peripheria rotae, non est mihi certum, nihilominus videtur, quod pari ratione concedendum sit, sicut conceditur procedens illatum. Thomas 1509, S. 138.
[...] distantia enim punctorum vel propinquitas nihil confert ad velocitatem circumgirationis nec auget nec minuit proportionem, sed dumtaxat impedimentum circumgirandi, quod forte est gravitas existens in corpore circunducto. Si nulla enim esset gravitas aut aliquod aliud impedimentum, aeque cito giraretur magna rota sicut parva, et si potentia circumgirans esset naturalis, subito circumgiraretur. Thomas 1509, S. 138.
Vgl. Thomas 1509, S. 138.
[...] ad quam dico, quod motus talis lineae girativae non debet reduci ad uniformitatem, ut supponit replica, sed totum residuum illius lineae, quod est supra punctum, in quo est medius gradus motus, quo movetur totalis rota, debet capi, ac si esset medietas totius lineae, tam velociter enim movetur illa linea girativa sicut una linea recta exiens a centro rotae usque ad circumferetiam eius. Et ideo velocitas illius lineae girativae commensurari habet penes velocitatem talis lineae rectae. Thomas 1509, S. 138.
Argumentum in oppositum non est magis pro una opinione quam pro reliqua. Thomas 1509, S. 138.
Utrum omnis motus uniformiter difformis quoad tempus mensurari habet penes gradum medium, et omnis difformiter difformis quoad tempus penes reductionem ad uniformitatem sive p[e]nes commensurationem denominationis, qua denominatione denominat mobile moveri. Thomas 1509, S. 138.
Et arguitur primo, quod motus uniformiter difformis velocitas no[n] est grad[u] illius medio commensuranda. Thomas 1509, S. 139.
[...] quia sequeretur, quod omne, quod movetur in aliquo tempore uniformiter difformiter a non gradu usque ad certum gradum – id est a non gradu usque ad duo decimum – moveretur in duplo tardius quam mobile motum per idem tempus gradu duo decimo continuo, sed consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 139.
Sed contra, quia tunc sequeretur, quod omne movens uniformiter a non gradu usque ad certum gradum in triplo velocius moveretur in secunda medietate temporis quam in prima, sed consequens est falsum. Thomas 1509, S. 139.
Sed contra, quia si illa solutio esset bona, sequeretur, quod in secunda medietate primae medietatis in triplo velocius moveretur illud mobile quam in prima eiusdem medietatis, et divisa illa medietate adhuc in duas in subtriplo moveretur, sed consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 139.
[...] si quilibet motus uniformiter difformis commensurari debeat penes gradum medium, sequeretur, quod motus a certo gradu usque ad non gradum ut exempli gratia, quo aliquod mobile movetur a quarto usque ad non gradum remittendo motum suum in hora, et motus, quo aliquod mobile movetur uniformiter difformiter a non gradu usque ad quartum in eadem hora, essent omnino aequales, sed hoc est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 139.
Sed contra, quia tunc sequeretur, quod si motus ut 4 vel aliquis alter intendatur ad suum duplum uniformiter, et alter motus ei aequalis remit[t]atur in eadem hora ad non gradum sive ad quietem, tunc ille, qui remittitur in infinitum, velocius remittitur quam alter, qui intenditur intendatur. Quod tamen est falsum, cum tantam latitudinem unus acquirat, sicut alter deperdat. Thomas 1509, S. 140.
Dices et bene distinguendo illatum aut, quod in infinitum velocius remittatur in eodem tempore velocitate geometrica, et sic conceditur, aut arithmetica, et sic negatur. Thomas 1509, S. 140.
Sed contra, quia tunc sequeretur, quod non esset possibile, quod ita velociter geometrice intenderetur unus motus in tempore finito uniformiter, sicut motus ei aequalis remitteretur uniformiter ad non gradum in eodem tempore, sed consequens videtur falsum, (cum aequalem latitudinem unus motus deperdat, sicut alter acquirit), igitur illud, ex quo sequitur. Thomas 1509, S. 140.
[...] si motus uniformiter difformis corresponderet suo gradui medio, sequeretur, quando duo motus aequales uniformiter difformes remitterentur in hora, unus in duplo velocius altero, ille, qui tardius remittitur, quando est remissus ad subduplum, alter esset remissus ad subquadruplum et non ad quietem sive ad non gradum, sed consequens falsum, ut patet intuenti, igitur illud, ex quo sequitur. Thomas 1509, S. 140.
[...] si motus uniformiter difformis corresponderet gradui medio, sequeretur, quod si essent duo motus uniformiter difformes, aequales, incipientes ab eodem gradu, terminati ad eundem vel ad non gradum, et unus illorum, puta A, in duplo velocius continuo intenderetur quam alter, puta B, et talis intensio duraret in infinitum, quod aliquando A esset motus duplus ad B, sed consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 140.
[...] si omnis motus uniformiter difformis commensurari habet gradu medio, vel igitur in quolibet tali motu ille gradus medius est subduplus adaequate ad intensius extremum talis motus, vel maior subduplo, vel minor, nullum istorum est dicendum, igitur. Thomas 1509, S. 140.
In omni motu vero uniformiter difformi terminato utrimque ad gradum gradus medius est maior quam subduplus ad extremum intensius. Thomas 1509, S. 140.
Sed contra, quia tunc sequeretur, quod aliquando gradus medius alicuius motus uniformiter difformis utrimque terminati ad gradum esset subsesquitertius ad gradum summum, aliquando subsesquialterius, aliquando subsesquiquartus et sic in infinitum. Thomas 1509, S. 140.
Quod si concedis, sicut concedendum est, sequitur, quod nulla potest inveniri certa regula et universalis ad sciendum in quolibet motu uniformiter difformi, quanto plus pertransitur per totum motum in medietate intensiori quam in medietate remissiori, quod videtur satis inconveniens. Thomas 1509, S. 140.
[...] si prima pars et secunda quaestionis essent verae, sequeretur, quod aliqui duo motus sunt modo aequales, et in tempore aequali aequales latitudines deperdent successive, ita quod in fine illius temporis erunt aequales, et tamen per unum illorum motuum maius spatium continuo pertransitur quam per alium, hoc videtur impossibile, igitur illud, ex quo sequitur. Thomas 1509, S. 140f.
Et confirmatur supposito, quia una pars proportionalis proportione quadrupla est duae partes proportione dupla, et per consequens duae partes proportionales proportione quadrupla sunt 4 proportione dupla et sic consequenter procedendo per numeros pariter pares. Thomas 1509, S. 141.
Quo supposito sic argumentor ex casu in fine primae partis proportionalis proportione quadrupla B perdet primam partem proportionalem proportione dupla latitudinis deperdendae, et tunc A deperdit duas partes proportionales proportione dupla latitudinis deperdendae, quia tunc sunt transactae duae partes proportionales temporis proportione dupla, ut patet ex supposito, et A motus remittitur uniformiter, ut patet ex casu. Thomas 1509, S. 141.
In fine vero secundae partis proportionalis temporis proportione quadrupla B deperdit duas partes proportionales latitudinis deperdendae proportione dupla, et A 4, quam illae duae partes proportione quadrupla sunt quatuor partes pr[o]portionales proportione dupla, igitur continuo maior latitudo est deperdita A quam ipsi B usque ad instans terminativum, et sic semper in quolibet instanti intrinseco illius horae motus B est velocior motu A. Quod fuit probandum. Thomas 1509, S. 141.
Immo conceditur, quod in principio illi motus sunt aequales et in fine aequales, et aequalem latitudinem adaequate deperdunt in eodem tempore, et tamen in toto illo tempore unus est intensior altero, ut pulchre probat argumentum. Thomas 1509, S. 141.
Sed contra, si solutio veritati esset consona, talis ex ea duceretur conclusio, quod videlicet aliqui duo motus se habent modo in proportione dupla et per idem tempus uniformiter et aeque velociter remitterentur adaequate, et tamen semper in illo tempore spatium pertransitum a maiori erit plusquam duplum ad spatium pertransitum a minori, sed consequens videtur falsum, cum illo modo se habent in proportione dupla et semper aequaliter remittuntur. Thomas 1509, S. 141.
Apparet igitur, quod continuo manebunt se habentes in proportione dupla, et sic spatium pertransitum a maiori non est plusquam duplum ad spatium pertransitum a minori, et sic illud consequens est falsum, et per consequens illud, ex quo sequitur, probatur tamen sequela, et pono casum, quod sint A et B motus, et A sit duplus ad B, et remittantur continuo aeque velociter et uniformiter A et B perdendo aequalem latitudinem omnino per totum tempus. Thomas 1509, S. 141.
[...] si motus difformiter difformis commensurari haberet penes reductionem ad uniformitatem aut penes denominationem suae intensionis, sequeretur haec conclusio, quod videlicet aliquis esset motus difformis, qui non posset ad uniformitatem reduci, et cuius non posset dari certa intensio, consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 141.
Et generaliter observandum est, quod in quacumque proportione se habet pars temporis ad totum tempus, in eadem se habet velocitas motus in [i]lla parte ad velocitatem totalis motus in toto tempore. Thomas 1509, S. 142.
Dices forte et bene concedendo, quod talis motus non potest dari determinata intensio, et rationalis reductio ad uniformitatem, ita quod intensio illius motus se habeat ad motum alicuius illarum partium in proportione aliqua rationali, nec hoc est inconveniens, nec contra titulum quaestionis, quia intelligitur titulus quaestionis, dummodo partes, in quibus tales motus ponuntur, se habeant in proportione rationali. Thomas 1509, S. 142.
Sed contra solutionem arguitur sic, quia aliquis est motus difformis, cuius partes sunt in partibus temporis rationalem proportionem habentibus ad totum tempus, et tamen talis motus non valet reduci ad uniformitatem, nec valet inveniri certa eius intensio, igitur solutio nulla. Thomas 1509, S. 142.
Sed contra, quia tunc sequeretur, quod si hora dividatur per partes proportionales proportione tripla, et per primam illarum moveatur aliquod mobile aliquantula velocitate et per secundam dupla velocitate et per tertiam tripla et sic in infinitum ut in priori casu. Tale mobile etiam moveretur in totali hora adaequate dupla velocitate ad velocitatem, qua movetur in prima parte proportionali horae, sed consequens est falsum, igitur illud, ex quo sequitur. Thomas 1509, S. 142.
[...] aliquis est motus difformiter difformis, cuius non est dabilis uniformitas, nec denominationis intensio, igitur titulus quaestionis falsus. Thomas 1509, S. 142.
Sed contra mutando paululum casum, volo, quod A in prima proportionali horae proportione dupla aliquantulum velociter moveatur et in secunda in sesquialtero velocius quam in prima et in tertia in sesquitertio velocius quam in prima et in quarta in sesquiquarto velocius quam in prima et sic consequenter procedendo per omnes species proportionis superparticularis semper referendo ad primam partem. Thomas 1509, S. 143.
Quo posito arguitur sic: talis motus est difformiter difformis quoad tempus et non valet ad uniformitatem reduci aut certa eius intensio eius inveniri, igitur minor patet, quia non apparet modus, quo ille motus posset ad uniformitatem reduci, et si adversarius hoc neget, det illum modum, et in dubie facile erit calculatori philosopho illum impugnare. Thomas 1509, S. 143.
[...] si aliquod mobile moveatur in prima parte proportionali huius horae aliqua proportione aliquantulum velociter et in secunda in duplo velocius et in tertia in sesquitertio velocius quam in prima et in quarta in sesquiquinto velocius quam in prima et in quinta in sesquioctavo velocius et insequenti in sesquiduodecimo velocius et sic in infinitum procedendo interscalariter per species proportionis superparticularis continuo una pluries omittendo, tunc talis motus est difformiter difformis quoad tem[p]us, et non potest eius certa intensio dari. Thomas 1509, S. 143.
[...] et pono casum, quod in prima parte proportionali aliquod mobile moveatur aliquantulum velociter et in secunda in sesquialtero velocius quam in prima et in tertia in superbipartiente tertias velocius quam in prima et in quarta in sesquitertio velocius quam in prima et in quinta in super[tri]partiente quartas velocius quam in prima et in sexta in sesquiquarto velocius quam in prima et sic consequenter procedendo per omnes species proportionis superparticularis interserendo species proportionis suprapartientis, tunc tale mobile movetur difformiter quoad tempus, et tamen motus illius uniformitas non potest venari, igitur titulus quaestionis est falsus. Thomas 1509, S. 143.
[...] et pono casum, quod A mobile in prima parte proportionali moveatur aliquantulum et in secunda in duplo plus et in tertia in sesquialtero plus quam in prima et in quarta in superbipartiente tercias plus quam in prima et in quinta in duplo sesquialtero plus quam in prima et in sexta in duplo superbipartiente tertias velocius quam in prima et in septima in triplo velocius quam in prima et sic consequenter capiendo primo quinque et consequenter alias 5 et sic in infinitum. Thomas 1509, S. 143.
Quo posito illorum motus est difformiter difformis, et tamen illius velocitas non valet perscrutari. Thomas 1509, S. 143.
In oppositum tamen est universalis opinio communiter philosophantium, quae in hac parte multum vigoris acroboris habet. Praeterea per quemlibet talem motum difformem in totali tempore adaequate pertransitur aliquod spatium adaequate, et tale spatium in tali tempore ab aliqua velocitate uniformi natum est pertransiri, igitur illa velocitas uniformis est tanta, quanta est velocitas illius motus difformis, quo illud spatium in eodem tempore pertransitur adaequate. Thomas 1509, S. 143.
Vgl. Thomas 1509, S. 143.
Sed motus uniformiter difformis quoad tempus adhuc duplex est: nam quidam est uniformiter difformis terminatus ad non gradum in altero extremo, alter vero est uniformiter difformis utrobique ad gradum terminatus. Et de utroque istorum dicitur, quod gradui suo medio correspondet, id est gradui motus, quem habet in medio temporis. Nam quanto velocius movetur mobile motum uniformiter difformiter mediante medietate talis motus intensiori, tanto tardius movetur mediante medietate remissiori, et sic aeque velociter movetur, ac si moveretur gradu medio. Thomas 1509, S. 143f.
[...] in omni latitudine uniformiter difformi incipiente a gradu a terminata ad non gradum gradus medius est subduplus ad extremum intensius, ita quod si latitudo incipiat ad octavo et terminatur ad non gradum, gradus medius est gradus quartus, quia quartus gradus est s[u]bduplus ad octavum. Thomas 1509, S. 144.
[...] gradus medius motus uniformiter difformis utrobique ad gradum terminati est intensior quam subduplus ad extremum intensius. Thomas 1509, S. 144.
[...] cuiuslibet latitudinis motus uniformiter difformis terminati ad non gradum, medietas intensior est in triplo intensior medietate remissiori. Thomas 1509, S. 144.
[...] omnis potentia movens uniformiter difformiter latitudine terminata ad non gradum in triplo plus pertransit in medietate, in qua movetur intensius, quam in medietate temporis, in qua movetur remissius, ut si in medietate, in qua movetur remissius, pertransit unum pedale, in alia pertransit tripedale. Thomas 1509, S. 145.
[...] si A mobile moveatur per horam uniformiter difformiter incipiendo a non gradu usque ad certum gradum, et in prima medietate unam leucam pertransit, in secunda medietate trium leucarum spatium absolvet. Et si ordine praepostero moveri incepisset, puta ab illo dato gradu usque ad non gradum, in prima medietate horae tribus absolutis leucis, una dumtaxat restaret transeunda in secunda temporis medietate. Thomas 1509, S. 145.
[...] si aliquod mobile moveatur uniformiter difformiter a non gradu usque ad certum gradum in aliquo tempore, ipsum adaequate subduplum spatium pertransit ad spatium natum pertransiri illo gradu intensiori per idem tempus continuato. Thomas 1509, S. 145.
[...] omne mobile motum uniformiter difformiter a certo gradu usque ad certum gradum in aliquo tempore maius spatium quam subduplum pertransit in eodem tempore ad spatium natum pertransiri mediante extremo intensiori illius latitudinis per idem tempus continuato. Thomas 1509, S. 145.
[...] si aliquod mobile uniformiter difformiter moveatur a certo gradu intensiori ad ce[r]tum gradum remissiorem in hora, ipsum in prima medietate horae minus quam triplum spatium pertransit ad spatium pertransitum in secunda medietate horae, in qua tardius movetur. Thomas 1509, S. 145.
[...] quomodo cognoscendum sit in omni latitudine motus utrimque ad gradum terminata, in qua proportione se habeat extremum intensius ad gradum medium eiusdem latitudinis, et in qua proportione plus pertransitur mediante medietate intensiori talis latitudinis quam mediante medietate remissiori. Thomas 1509, S. 145.
R[e]spondeo, quod in hac materia nulla potest dari certa et universalis regula. Quoniam secundum, quod extremum intensius et remissius se habent in alia et alia proportione ad invicem, ita se habet g[r]adus medius ad extremum intensius talis latitudinis in alia et alia proportione, tamen possent sig[n]ari peculiares regulae certis speciebus proportionum accommode. Thomas 1509, S. 145.
Quaereret tamen aliquis ulterius, quo tramite et mensura posset facile investigari gradus medius in omni latitudine. Respondeo, quod per hanc regulam, quia aut latitudo illa terminatur ad non gradum, tunc dividatur extremum intensius per medium, et una medietas est gradus medius. Si vero incipit a gradu et terminatur ad gradum, tunc subduplum ad aggregatum ex extremo intensiori et remissiori est gradus medius inter illa extrema. Thomas 1509, S. 145.
Notandum est secundo, quod motu[u]m velocitates – quandoque sunt aequales, quandoque inaequales intensive – et si aequales, aut coextensae [sunt] partibus temporis aequalibus aut inaequalibus. Thomas 1509, S. 145.
Si vero inaequales, idem etiam contingit, quia aut extenduntur per tempora aequalia aut per inaequalia. Thomas 1509, S. 145.
Si sint inaequales inaequalibus coextensae temporibus, hoc contingit dupliciter, quia aut maior velocitas coextenditur tempori maiori aut minori. Thomas 1509, S. 145.
Exemplum primi: ut si velocitas ut 4 coextendatur uni horae, hoc est, mobile moveatur ut 4 per unam horam et ut duo per dimidiam. Exemplum secundi: ut si aliquod mobile moveatur velocitate ut quatuor per mediam horam et velocitate ut duo per horam. Thomas 1509, S. 145f.
Item si maior velocitas coextendatur tempori minori, et minor maiori, hoc co[n]tingit tripliciter, quia aut proportio temporum excedit proportionem velocitatum, aut proportio velocitatum excedit proportionem temporum, aut proportiones temporum et velocitatum sunt aequales. Thomas 1509, S. 146.
Exemplum primi: ut si aliquod mobile in hora moveatur ut duo et in quarta horae ut quatuor, tunc proportio temporum excedit proportionem velocitatum. Nam ipsa temporum proportio quadrupla est, velocitatum vero dupla, ut patet aspicienti. Thomas 1509, S. 146.
Exemplum secundi: ut si mobile moveatur ut unum per horam et in media ut 3, tunc proportio temporum est dupla, velocitatum vero tripla, exsuperat igitur velocitatum proportio temporum proportionem. Thomas 1509, S. 146.
Exemplum tertii: ut si aliquod mobile moveatur in hora ut unum, et aliud in media ut duo, constat proportionem temporum proportioni velocitatum aequari, utraque enim dupla est, et velocitatum et temporum. Thomas 1509, S. 146.
Si velocitates sint aequales aequalibus coextensae temporibus, mobilia in eisdem mota aequalia spatia in eisdem temporibus absolvunt (ceteris aliis deductis), ut puta rarefactione, condensatione spatii et praepostera motione, ut conclusiones sexto physicorum ostendunt. Si vero velocitates aequales per inaequalia labantur tempora, tunc in ea proportione mobile in maiori tempore maius spatium pertransit quam in minori, in qua ipsum maius tempus se habet ad minus. Thomas 1509, S. 146.
Quando inaequales velocitates aequalibus temporibus coextenduntur, tunc mobile, quod maiore velocitate movetur, in ea proportione maius spatium pertransit quam alterum mobile, in qua se habet velocitas maior ad minorem. Thomas 1509, S. 146.
Si inaequales velocitates in aequalibus temporibus coextenduntur, et maior velocitas maiori tempori coextendatur, et minor minori, tunc mobile, quod movetur in maiori tempore, maius spatium pertransit in proportione composita temporis maioris ad tempus minus et velocitatis maioris ad velocitatem minorem. Thomas 1509, S. 146.
Ex hac propositione sequitur primo, quod si A moveatur per unam horam velocitate ut 6, et B per mediam horam velocitate ut 4, quod spatium pertransitum ab A erit triplum ad spatium pertransitum a B. Thomas 1509, S. 146.
Sequitur secundo, quod si A mobile moveatur per horam velocitate ut 6, et B per duas tertias horae velocitate ut 4, quod in minori proportione maius spatium pertransit A quam B quam in priori casu. Thomas 1509, S. 146.
[...] si maior velocitas tempori minori coextendatur, et minor maiori, et proportio velocitatis maioris ad velocitatem minoris sit aequalis proportioni temporis maioris ad tempus minus, tunc illa mobilia aequalia spatia pertranseunt. Thomas 1509, S. 147.
[...] si A mobile moveatur per horam velocitate ut 4, et B mobile per duas tertias horae velocitate ut sex, B et A aequalia spatia pertranseunt. Thomas 1509, S. 147.
[...] si maior velocitas tempori et extendatur minori, et minor velocitas maiori tempori, proportioque velocitatis temporis proportionem exsuperet, tunc mobile minori tempore motum maius spatium describet quam mobile motum in maiori tempore in ea proportione, per quam velocitatum proportio temporum proportionem excedit. Thomas 1509, S. 147.
Ex hac propositione sequitur, quod si A mobile moveatur per horam velocitate ut duo, et B mobile per mediam horam velocitate ut 6, quod B mobile in sesquialtero maius spatium pertransit quam A, ut si A pertransit bipedale, B tripedale pertransit. Thomas 1509, S. 147.
[...] ubicumque maior velocitas tempori coassistit minori, minor vero maiori, estque proportio velocitatum temporum proportione inferior et minor, tunc mobile, quod maiori velocitate moventur, minori tempore minorem magnitudinem describet quam mobile motum maiori tempore in ea proportione, per quam temporum proportio velocitatum proportioni effertur. Thomas 1509, S. 147.
Quandocumque duo numeri inaequales habent duas proportiones ad unum tertium, tunc in ea proportione minor illorum est minor maiore, per quam maior proportio excedit minorem, id est, per quam proportio maioris numeri ad illud tertium excedit proportionem minoris numeri ad idem tertium. Quoniam proportio maioris ad idem tertium componitur ex proportione illius ad numerum minorem, et numeri minoris ad idem tertium. Thomas 1509, S. 147f.
[...] si equus A moveretur velocitate ut 4 in hora adaequate, et equus B velocitate ut 6 adaequate in media hora, et ipse equus B 6 leucas pertranseat in illa media hora, necesse est equum A ad extremum 8 leucarum in hora devenire. Thomas 1509, S.144.
[...] aliud est latitudinem motus uniformiter intendi aut uniformiter remitti, aliud vero mobile uniformiter moveri. Thomas 1509, S. 148.
Unde cum latitudo motus uniformiter intenditur a non gradu vel a gradu ad certum gradum, semper mobile uniformiter difformiter movetur. Et similiter quando uniformiter remittitur aliquis motus a gradu usque ad non gradum vel certum gradum, tunc mobile uniformiter difformiter movetur. Nam latitudo motus si acquisita aut deperdita coextenditur uniformiter difformiter temporis partibus, ita quod illius motus cuiuslibet partis gradus medius tanto exceditur a summo, quantum excedit infimum vel non gradum, quare definitive arguendo relinquitur omnem talem motum sic uniformiter acquisitum vel deperditum esse uniformiter difformem. Thomas 1509, S. 148.
Insuper adverte, quod latitudo motus tripliciter acquiri potest, ut ad propositum nostrum sufficit, vel deperdi. Thomas 1509, S. 148.
Primo modo latitudo motus potest acquiri vel deperdi continuo uniformiter, ut puta quando mobile in partibus aequalibus temporis aequales gradus velocitatis acquirit vel deperdit continu[o]. Thomas 1509, S. 148.
Secundo potest latitudo motus acquiri vel deperdi continuo velocius et velocius, ut puta quando mobile in qualibet parte sequenti temporis continuo maiorem latitudinem motus deperdit quam in aequali praecedenti. Thomas 1509, S. 148.
Tertio modo potest latitudo motus sive velocitas acquiri vel deperdi continuo tardius et tardius, ut puta quando mobile continuo in qualibet parte sequenti temporis minorem latitudinem motus deperdit quam in aequali praecedente. Thomas 1509, S. 148.
[...] si aliquis motus uniformiter continuo intendatur vel remittatur a certo gradu usque ad certum gradum vel ad non gradum, eius velocitas gradui medio correspondet. Thomas 1509, S. 148.
[...] omnis motus continuo velocius et velocius intensus correspondet quantum ad velocitatem gradui remissiori medio gradu inter extremum intensionis eius in principio motus et inter extremum intensionis in fine motus. Thomas 1509, S. 148.
Et confirmatur, quia A et B in principio sunt motus aequales, et in toto tempore debent acquirere aequales latitudines, et in quolibet instanti intrinseco est plus acquisitum ipsi A quam B illius latitudinis acquirendae, igitur continuo A motus est maior B. Thomas 1509, S. 149.
[...] omnis motus velocius et velocius deperditus quantum ad transitionem spatii inte[n]siori gradui gradu medio correspondet, hoc est, tale mobi[l]e motum illo motu maius spatium in illo tempore pertransit adaequate, quam si gradu medio inter extrema illius motus continuo uniformiter moveretur in illo tempore. Thomas 1509, S. 149.
[...] si A mobile moveatur in hora incipiendo ab octavo usque ad quartum continuo uniformiter remittendo motum suum, et B mobile moveatur etiam in hora ab octavo usque ad quartum continuo velocius et velocius remittendo motum suum, et A pertransit 6 pedalia, B pertransibit plusquam sex pedalia. Thomas 1509, S. 149.
[...] si A incipiat moveri ab octavo usque ad quartum uniformiter, et B in eodem tempore moveatur incipiendo a decimo sexto usque ad duodecimum perdendo latitudinem 4 graduum velocius et velocius, tunc continuo B movebitur plusquam in duplo velocius A, et continuo pertransibit plusquam duplum spatium ad spatium in eodem tempore pertransitum ab A. Thomas 1509, S. 149.
[...] si tam [A] quam B remitterentur ad suum subduplum in hora, ita quod A deperdat in hora continuo uniformiter quatuor gradus, et B octo continuo velocius et velocius, sequitur, quod B plusquam duplum spatium in hora pertransibit quam A. Thomas 1509, S. 149.
[...] omnis motus tardius et tardius intens[]us quantum ad pertransitionem spatii gradui intensiori medio correspondet. Thomas 1509, S. 149.
[...] omnis motus tardius et tardius deperditus gradui remissiori medio correspondet. Thomas 1509, S. 149.
[...] si mobile A moveatur uniformiter difformiter ab octavo usque ad quartum perdendo latitudinem motus ut 4 uniformiter continuo in hora, et mobile B moveatur in eadem hora ab octavo usque ad quartum perdendo etiam latitudinem ut 4 continuo tardius et tardius, tunc si A pertranseat 6 pedalia, B pertransibit minus. Thomas 1509, S. 150.
[...] omnis latitudo motus consimiliter omnino perdita et acquisita uni gradui omnino correspondet. Volo dicere, quod si sit aliquis motus, qui gratia exempli incipiat a non gradu et intendatur usque ad octavum in hora adaequate uniformiter, et alter motus vel idem remittatur in hora uniformiter, sicut intendebatur, ab octavo usque ad non gradum, tales motus eidem gradui correspondet. Thomas 1509, S. 150.
[...] velocitates motuum dupliciter investigari posse, videlicet ex commensuratione spatiorum pertransitorum, et hoc ab effectu et a posteriori, quod in praesenti tractatu inquirimus, alio vero modo ex commensuratione et proportionalitate proportionum, a quibus proveniunt velocitates illae. Thomas 1509, S. 150.
[...] quavis velocitate data et quacumque proportione proposita, cuiusdam artis ingenio investigari potest, an data velocitas a proposita proportione aut a minori aut maiore proveniat. Thomas 1509, S. 150.
[...] captis duabus potentiis inaequalibus moventibus eandem resistentiam et scita proportione inter illas potentias, scita etiam proportione, in qua maior potentia velocius movet resistentiam, quam minor moveat eandem, artificio quodam reperitur, quanta est proportio maioris potentiae ad resistentiam, et etiam minoris potentiae ad eandem resistentiam. Thomas 1509, S. 151.
[...] data quavis potentia movente duas resistentias inaequales, inter quas resistentias est proportio nota, notumque est, in qua proportione velocius data potentia moveat minorem quam maiorem, mathematica industria proportiones potentiae ad utramque resistentiam, quales videlicet existant, investigare licebit, ut si Socrates proiiciat in aliquo tempore lapidem A et in eodem vel aequali lapidem B minorem, inter quos lapides est proportio nota gratia argumenti dupla, moveatque Socrates illos lapides ab eadem virtute, sitque scitum, quod moveat Socrates B lapidem in triplo velocius quam A lapidem gratia exempli, iam investigare intendimus ingenio artis mathematicae, quae est illa proportio, a qua Socrates movet B lapidem, et quae sit illa, a qua moveat A lapidem, utrum videlicet dupla an tripla aut aliqua alia, quia hoc ignotum est. Thomas 1509, S. 151.
[...] si Socrates moveat B lapidem per tantum spatium, quantus est diameter quadrati, et A lapidem per tantum spatium, quanta est costa eiusdem quadrati, tunc proportio Socratis ad A lapidem, id est, a qua movet A lapidem, est plusquam dupla ad proportionem duplam, et proportio, qua Socrates movet B lapidem, est plusquam tripla ad duplam. Thomas 1509, S. 151.
[...] illa proportio Socratis ad B est plusquam octupla. Est enim octupla adaequate tripla ad duplam, ut patet ex octava conclusione sexti capitis secundae partis, et illa Socratis ad B maior quam tripla ad duplam, ut probatum est. Thomas 1509, S. 151.
[...] data quavis velocitate quavisque signata proportione arithmetico apparatu an proportio, a qua provenit illa velocitas, proportioni signatae commensurabilis existat, an non, opere pretium erit investigare. Thomas 1509, S. 151.
[...] diviso aliquo corpore sive latitudine per partes proportionales, quavis libuerit, proportione totum illud corpus sive latitudo se habet ad residuum a prima parte proportionali in ea proportione, qua ipsum sive latitudo ipsa dividitur. Thomas 1509, S. 152.
[...] diviso aliquo tempore per partes proportionales quavis proportione, et sit aliquod mobile, quod aliquanta velocitate moveatur in prima parte proportionali et in secunda in duplo maiori quam in prima et in tertia in triplo maiori quam in prima et in quarta in quadruplo maiori et sic consequenter ascendendo per omnes species proportionis multiplicis, talis velocitas totius illius temporis et omnium illarum partium proportionalium se habet ad velocitatem primae partis proportionalis in ea proportione, in qua se habet totum illud tempus sic divisum in ordine ad primam partem proportionalem. Thomas 1509, S. 152.
[...] divisa hora vel tempore aliquo, quavis proportione F volueris, et in prima parte proportionali talis proportionis mobile aliquod moveatur adaequate certa velocitate, et aliud mobile vel idem in tota illa hora vel tempore moveatur eadem velocitate, tunc in quacumque proportione se habuerit tempus ad primam partem proportionalem, in ea proportione se habebit spatium absolutum sive pertransitum in toto tempore ad spatium pertransitum in prima parte proportionali. Thomas 1509, S. 153.
[...] divisa hora, quavis proportione volueris, in partes proportionales et in prima illarum partium proportionalium mobile aliquod aliquanta velocitate moveatur et in secunda in duplo maiori velocitate quam in prima et in tertia in triplo maiori quam in prima et sic consequenter, tunc illo casu totalis velocitas se habebit ad velocitatem primae partis proportionalis in ea proportione, in qua se habebit totum tempus ad primam partem proportionalem eius, et spatium in toto tempore adaequate pertransitum se habebit ad spatium absolutum in prima parte proportionali in proportione duplicata. Thomas 1509, S. 153.
[...] velocitatis totius horae ad velocitatem primae partis proportionalis est proportio F, et temporis totius horae, quod est maius, ad tempus primae partis proportionalis est etiam F proportio, ergo spatii pertransiti in tota hora ad spatium pertransitum in prima parte proportionali est proportio composita ex duplici proportione F, et per consequens spatium pertransitum in tota hora ad spatium pertransitum in prima parte proportionali est proportio dupla ad proportionem velocitatum, quae est F. Thomas 1509, S. 154.
[...] divisa hora per partes proportionales proportione multiplici, sive dupla, sive tripla, sive quadrupla, sive quavis alia multiplici, et in prima parte proportionali aliquod mobile moveatur aliquantulum et in secunda in duplo maiori velocitate quam in prima et in tertia in triplo quam in prima, ut praecedentis theorematis casus ostendit, totius illius velocitatis ad velocitatem primae partis proportionalis erit proportio dupla, si divisio facta fuerit proportione dupla et sesquialtera, si tripla, et sesquitertia, si quadrupla, et sic in infinitum ascendendo seriatim per species proportionis superparticularis et multiplicis. Thomas 1509, S. 154.
[...] divisa hora per partes proportionales proportione sextupla, et in prima illarum moveatur aliquod mobile aliquanta velocitate et in secunda in duplo maiori et in tertia in triplo modo saepius recitato, tunc totius velocitatis ad velocitatem primae partis proportionalis est proportio sesquiquinta, et spatii pertransiti in tota hora ad spatium pertransitum in prima parte proportionali est proportio supra undecimpartiens vicesimas quintas. Thomas 1509, S. 154.
[...] divisa hora per partes proportionales proportione octupla, et in eisdem moveatur aliquod mobile modo pluries resumpto, totius velocitatis ad velocitatem primae partis proportionalis est proportio sesquiseptima, et spatii pertransiti in tota hora ad spatium pertransitum in prima parte proportionnali erit proportio dupla ad sesquiseptima, quae est super quindecimpartiens quadragesimas [nonas], cuiusmodi est 9 cum septima ad 7 et 64 ad 49. Thomas 1509, S. 154.
[...] divisa hora per partes proportionales proportione superparticulari sesquialtera, sesquiquarta seu quavis alia superparticulari distributaque velocitate partibus illis proportionalibus, ita ut mobile in prima illarum moveatur aliqnantulum et in secunda in duplo velocius et in tertia in triplo velocius quam in prima et sic consequenter in casu saepius repetito, tunc tota velocitas se habet ad velocitatem primae partis proportionalis in proportione tripla, si fuerit hora divisa in proportione sesquialtera. Si vero fuerit divisa in proportione sesquitertia, in proportione quadrupla, si in proportione sesquiquarta, in proportione quintupla et sic consequenter ascendendo seriatim per species proportionis superparticularis et multiplicis. Et spatia pertransita in totali tempore ad spatia primae partis proportionalis se habent in proportione duplicata (duplicata inquam ad triplam sive dupla ad triplam, si fuerit divisio facta in proportione sesquialtera, et quadrupla, si fuerit facta divisio in proportione sesquitertia et sic consequenter.) Thomas 1509, S. 154.
[...] divisa hora per partes proportionales proportione superparticulari, quavis libuerit, distributaque velocitate, ut in casu secundae conclusionis ponitur, ita videlicet, quod mobile in prima parte proportionali moveatur aliquantulum et in secunda in duplo velocius et in tertio in triplo velocius quam in prima et in quarta in quadruplo velocius quam in prima et sic consequenter, tunc tota velocitas erit aequalis velocitati tertiae partis proportionalis, si fuerit facta divisio proportione sesquialtera, et si fuerit divisio facta sesquitertia, tota velocitas erit aequalis velocitati quarta partis proportionalis, et si fuerit facta divisio proportione sesquiquarta, erit aequalis velocitati quintae partis proportionalis et sic consequenter ascendendo per species proportionis superparticularis et per partes proportionales. Thomas 1509, S. 155.
[...] hora divisa per partes proportionales proportione sesquialtera et mobile A in prima parte moveatur aliquantulum et in secunda parte in duplo velocius et in tertia in triplo velocius qua[m] in prima et sic consequenter, ut in prima parte proportionali pertransit unum pedale, in tota hora p[ert]ransit novem. Thomas 1509, S. 155.
[...] divisa hora vel tempore aliquo proportione quavis superparticulari, ut positum est in primo correlario, spatii pertransiti in tota hora ad spatium pertransitum in prima parte est proportio dupla ad proportionem, quam habet velocitas tertiae partis ad velocitatem primae partis si fuerit divisio facta proportione sesquialtera. Si vero fiat proportione sesquitertia in proportione, dupla ad proportionem velocitatis quartae partis ad velocitatem prime. Si sesquiquarta in proportione, dupla ad proportionem velocitatis quintae partis ad velocitatem primae et sic consequenter. Thomas 1509, S. 155.
[...] hora divisa per partes proportionales proportione aliqua superparticulari, quavis volueris, et aliquod mobile moveatur in prima et cetera, ut positum est, spatii pertransiti est tota hora est noncuplum ad spatium pertransitum in prima parte proportionali, si fuerit divisio facta proportione sesquialtera, si vero {proportione} sequitertia, est sexdecuplum, si autem proportione sesquiquarta, est vicecuplum quintuplum, ita quod in prima parte pertransit unum [et] pedale in tota hora viginti quinque pedalia et sic consequenter. Thomas 1509, S. 155.
[...] divisa hora, quavis proportione libuerit, et in quacumque proportione se habuerint duae partes immediatae, in eadem proportione vel maiori se habuerit velocitas minoris partis ad velocitatem maioris, tota illa velocitas est infinita, spatiumque pertransitum pari ratione infinitum erit. Thomas 1509, S. 155.
[...] si hora dividatur per partes proportionales proportione dupla, ut mobile moveatur in prima parte aliquantulum et in secunda in duplo velocius quam in prima et in tertia in duplo velocius quam in secunda et in quarta in duplo velocius quam in tertia, spatium pertransitum erit infinitum. Thomas 1509, S. 155.
[...] partita hora per partes proportionales proportione sesquitertia, et in prima parte proportionali A mobile moveatur aliqua velocitate et in secunda in sesquialtero velocius quam in prima et in tertia in sesquialtero velocius quam in secunda et in quarta in sesquialtero velocius quam in tertia et sic consequenter, spatium pertransitum in tota hora erit infinitum. Thomas 1509, S. 155f.
[...] si hora fuerit divisa per partes proportionales proportione aliqua suprapartienti, et continuo velocitates partium proportionalium immediatarum, puta velocitas minoris partis ad velocitatem maioris se habuerit in aliqua proportione multiplici vel multiplici superparticulari vel multiplici superpartienti, spatium pertransitum in tota hora erit infinitum. Thomas 1509, S. 156.
[...] partita hora per partes proportionales, qua libuerit proportione, mobil[i] continuo movente velocius in parte sequenti quam in parte praecepenti, velocius nihilominus in proportione minori, quam sit proportio divisionis, spatium pertransitum in tota hora se habebit ad spatium pertransitum in prima parte proportionali in proportione, qua aliquod totum divisum proportione, qua maior proportio temporis excedit proportionem velocitatum, se habet in ordine ad primam partem proportionalem. Thomas 1509, S. 156. Alvarus Thomas betont im Folgenden, dass diese conclusio besondere Erläuterung bedarf.
[...] partitione horae facta per partes proportionales proportione quadrupla, velocitatibus continuo se habentibus in proportione dupla, ita quod velocitatis secundae partis proportionalis ad velocitatem primae sit proportio dupla, et velocitatis tertiae ad velocitatem secundae sit etiam proportio dupla et cetera, spatium pertransitum in tota hora est duplum ad spatium pertransitum in prima parte proportionali. Thomas 1509, S. 156.
[...] divisa hora per partes proportionales proportione supertripartienti quartas, cuiuslibet partis velocitate se habente ad velocitatem partis maioris immediate praecedentis in proportione sesquialtera spatium pertransitum in tota hora se habet ad spatium pertransitum in prima parte proportionali in proportione septupla, absolutoque pedali in prima parte, septem pedalia in tota hora absolventur. Thomas 1509, S. 157.
[...] partita hora per part[]es proportionales quavis proportione volueris, et in certa proportione continuo velocius mobile moveatur in parte praecedente maiore quam in immediate sequenti minori, spatium pertransitum in totali hora se habebit ad spatium pertransitum in prima parte proportionali in proportione, qua se habet aliquod totum divisum in partes proportionales proportione composita ex proportione temporis, puta partis proportionalis maioris ad partem immediate sequentem minorem, et [ex proportione] velocitatis partis maioris ad velocitatem partis minoris ad primam partem pr[o]portionalem talis divisionis. Thomas 1509, S. 157.
[...] partitione horae facta per partes proportionales proportione suprabipartiente tertias et in prima parte propor[ti]onali moveatur aliquod mobile aliquanta velocitate et in secunda in suprabipartiente quintas minore et in tertia in eadem proportione suprabipartiente quintas minore velocitate quam in secunda et sic consequenter, tunc spatium pertransitum in totali hora se habet ad spatium pertransitum in prima parte proportionali in proportione supertripartiente quartas, qualis est 7 ad 4. Thomas 1509, S. 157f.
[...] divisa hora per partes proportionales proportione dupla, mobili continuo in duplo tardius movente in parte sequenti minori quam in parte maiori immediate praecedenti illam spatium pertransitum in totali hora se habet ad spatium pertransitum in prima parte proportionali horae in proportione sesquitertia. Thomas 1509, S. 158.
[...] divisa hora in partes proportionales proportione tripla mobilique continuo in quadruplo tardius movente in parte sequenti minori quam in immediate praecedenti eam spatium pertransitum in totali hora se habebit ad spatium pertransitum in prima parte proportionali in proportione sesquiundecima, pertransitoque pedali in prima, duodecim undecimas pedalis in totali hora absolvet. Thomas 1509, S. 158.
[...] divisa hora per partes proportionales quavis proportione et in certa proportione continuo mobile velocius moveatur in qualibet parte pari sequenti quam in pari immediate praecedenti eam et similiter in certa proportione aequali, maiori vel minori continuo in qualibet parte sequente impari velocius moveatur quam in impari immediate praecedenti, spatium pertransitum in totali hora erit infinitum, dummodo proportio velocitatum sit aequalis proportioni temporum vel maior, et si proportio velocitatum partium parium et proportio velocitatum partium imparium fueri[n]t minor[es] proportione temporum, tunc spatium pertransitum in omnibus partibus paribus se habet ad spatium pertransitum in prima illarum parium in proportione, qua se habet aliquod totum divisum per partes proportionales proportione, per quam proportio temporum excedit proportionem velocitatum, ad primam partem proportionale eiusdem totius. Et similiter dicendum est de spatio pertransito in omnibus partibus imparibus. Thomas 1509, S. 158.
[...] partita hora per partes proportionales proportione dupla et in prima illarum mobile moveatur aliquanta velocitate u[n]iformiter, et in secunda moveatur uniformiter intendendo motum suum a gradu, quo movetur in prima, usque ad gradum duplum, et in tertia moveatur illo gradu duplo uniformiter, et in quarta intendat uniformiter motum suum ab illo gradu duplo usque ad gradum duplum illius, ita quod in omnibus partibus imparibus moveatur uniformiter continuo in duplo velocius in sequente impari quam immediate praecedenti impari, et in qualibet parte pari moveatur intendendo motum suum uniformiter a gradu partis imparis immediate praecedentis usque ad gradum partis {imparis} immediate sequentis, ita quod velocitates partium imparium reductae ad uniformi[t]atem, etiam si habeant continuo in proportione dupla, tunc spatium totale pertransitum in hora se habebit in proportione tripla sesquialtera ad spatium pertransitum in prima parte proportionali impari. Thomas 1509, S. 158.
[...] divisa hora per partes proportionales proportione quadrupla, et in prima parte moveatur mobile aliquanta velocitate uniformiter, et in secunda intendat motum sum uniformiter ab illo gradu, quo movetur in prima, usque ad triplum, et in tertia moveatur uniformiter illo triplo gradu, et in quarta moveatur uniformiter intendendo motum suum a gradu, quo movebatur in tertia, usque ad triplum illius et sic consequenter semper in qualibet pari intendendo gradum immediate praecedentis imparis usque ad triplum eiusdem gradus uniformiter, spatium pertransitum in totali hora se habebit ad spatium pertransitum in prima parte proportionali impari in proportione supra undecimpartiente tridecimas. Thomas 1509, S. 159.
[...] partita hora per partes proportionales proportione quadrupla et mobile in qualibet parte sequente impari in quadruplo velocius moveatur quam in immediate praecedenti impari, et in qualibet sequenti pari etiam in quadruplo velocius moveatur quam in immediate praecedenti pari, et in duplo velocius in prima parte pari quam in prima impari, tunc totale spatium pertransitum in hora se habet ad spatium pertransitum in prima parte proportionali impari in proportione dupla. Thomas 1509, S. 159.
[...] divisa hora per partes proportionales proportione dupla et A mobile in prima parte proportionali moveatur aliquantula velocitate et in secunda in sesquialtero maiori velocitate et in tertia in sesquiquarto maiori velocitate quam in prima et in quinta in sesquisexdecimo maiori quam in prima et sic consequenter ascendendo per species proportionis superparticularis denominatas a numeris pariter paribus, (melius tamen diceretur descendendo, quia proportiones superparticulares sunt minores, quanto a maiori numero denominantur, hoc est a parte aliquota denominata a maiori numero), spatium pertransitum in totali hora se habet ad spatium pertransitum in prima parte proportionali in proportione dupla sesquitertia. Thomas 1509, S. 160.
[...] si fuerit hora divisa proportione dupla, et in prima illarum partium moveatur aliquod mobile aliquanta velocitate et in secunda in supertripartiente quartas maiori velocitate et in tertia in supertripartiente octavas maiori velocitate quam in prima et in quarta in supertripartiente sexdecimas maiori quam in prima et in quinta in supertripartiente tricesimas secundas maiori velocitate quam in prima et sic consequenter procedendo per species proportionis supertripartientis denominatas a numeris pariter paribus sive a partibus aliquotis denominatis ab illis numeris, spatium pertransitum in toto tempore est duplum sesquialterum ad spatium pertransitum in prima parte proportionali. Thomas 1509, S. 160f.
[...] partita hora per partes proportionales proportione dupla et in prima illarum mobile aliquod moveatur aliqua velocitate et in secunda illarum in sesquitertio maiori et in tertia in sesquisexto maiori quam in prima et in quarta in sesquiduodecuplo maiori quam in prima et sic consequenter ascendo per numeros pares continuo se habentes in proportione dupla exordiendo a numero ternario, hoc est per species proportionis superparticularis denominatas a partibus aliquotis denominatis ab illis numeris, spatium pertransitum in totali hora est duplum superbipartiens nonas ad spatium pertransitum in prima parte proportionali. Thomas 1509, S. 161.
[...] divisa hora per partes proportionales, quacumque libuerit proportione, et in prima mobile moveatur aliquanta velocitate et in secunda in sesquialtero maiori et in tertia in sesquitertia maiori quam in secunda et in quarta in sesquiquarta maiori quam in tertia et in quinta in sesquiquinto maiori quam in quarta et sic consequenter, et si non valeat regula universalis signari ad reperiendum spatium pertransitum in totali hora, nihilominus tamen qualibet specie divisionis horae signata potest certitudinaliter investigari spatium pertransitum in tota hora et proportio eius ad spatium pertransitum in prima parte proportionali. Thomas 1509, S. 162.
[...] si sit aliquod tempus divisum per partes proportionales proportione dupla, et in prima parte proportionali mobile moveatur aliquanta velocitate et in secunda in duplo velocius quam in prima et in tertia in sesquialtero velocius quam in prima et in quarta in sesquitertio velocius quam in prima et sic consequenter procedendo per omnes species proportionis superparticularis, spatium pertransitum in totali tempore est maius quam duplum ad spatium pertransitum in prima parte proportionali et minus quam quadruplum. Thomas 1509, S. 162f.
[...] si fuerit tempus divisum per partes proportionales proportione sesquialtera, et mobile moveatur eodem modo, quo dictum est in casu conclusionis, spatium pertransitum in totali hora erit maius quam triplum ad spatium pertransitum in prima parte proportionali,et minus quam non ocuplum. Thomas 1509, S. 163.
[...] hora divisa per partes proportionales proportione superbipartiente tertias, mobili moto in prima parte proportionali aliquantula velocitate et in secunda in proportione supertripartiente quartas velocius et in tertia in proportione supertripartiente octavas velocius quam in secunda et in quarta in proportione supratripartiente decimas sextas velocius quam in tertia et sic consequenter, spatium pertransitum in totali hora erit maius quam duplum sesquialterum ad spatium pertransitum in prima parte proportionali et minus quam sexdecuplum sesquiquartum. Thomas 1509, S. 163.
[...] divisa hora per partes proportionales tripla proportione et in prima parte proportionali mobile moveatur aliquantula velocitate et in secunda in suprabipartiente tertias maiori velocitate et in tertia in superbipartiente quintas maiore velocitate quam in prima et in quarta in superbipartiente septimas maiori quam in prima et in quinta in superbipartiente nonas maiori quam in prima et sic consequenter procedendo per species proportionis superbipartientis denominatas a numeris imparibus vel a partibus aliquotis a numeris imparibus denominatis, spatium pertransitum in totali hora est maius quam sesquialterum ad spatium pertransitum in prima parte proportionali et minus quam duplum sesquiquartum. Thomas 1509, S. 163.
[...] divisa hora per partes proportionales proportione quadrupla et in prima parte proportionali mobile moveatur aliquantula velocitate et in secunda in sesquialtero velocius et in tertia in superbipartienti tertias velocius quam in prima et in quarta in supertripartiente quartas velocius quam in prima et in quinta in superbipartiente quintas velocius quam in prima et in sexta in supertripartiente octavas velocius quam in prima et sic consequenter in partibus imparibus procedendo per proportionem supertripartientem et in paribus per proportionem superbipartientem, spatium pertransitum in totali hora est plusquam sesquitertium ad spatium pertransitum in prima parte proportionali et minus quam superseptipartiens nonas ad spatium pertransitum in prima. Thomas 1509, S. 163.
[...] si velocitas in infinitum difformis aliquam cohaerentiam sive proportionem continuo servat, facile est totalem velocitatem commensurare et spatium mediante illa transitum mentiri. Thomas 1509, S. 163.
[...] non habentibus illis velocitatibus difformibus aliquam continuo inter se proportionem, sicut sit in casu duodecimae conclusionis et sequentium correlariorum, impossibile est naturaliter intellectum finitae capacitatis talem velocitatem sic difformem ad uniformitatem redigere et adaequatum spatium pertransitum infallibili[t]er assignare. Thomas 1509, S. 163.
[...] partita hora per partes proportionales proportione dupla mobile in prima parte proportionali aliquantum velociter mov[e]atur et in secunda in sesquialtero velocius et in tertia in sesquiquinto et in quarta in sesquioctavo quam in prima et sic consequenter procedendo per species proportionis superparticularis interscalariter continuo duos omittendo. Thomas 1509, S. 164.
[...] item si divisa hora per partes proportionales proportione tripla A mobile in prima parte proportionali moveatur aliquantulum et in secunda in sesquiquinto velocius et in tertia in sesquinono velocius quam in prima et in quarta in sesquitridecimo velocius quam in prima et in quinta in se[squi]decimo septimo velocius quam in prima et sic consequenter procedendo per species proportionis superparticularis continuo omittendo tres, item sic procedendo continuo omittendo quatuor, item omittendo continuo quinque et 6 et 7 et sic consequenter, infinitae dabuntur velocitates difformes, quarum uniformitas a nobis nequaquam naturaliter reperiri potest. Thomas 1509, S. 164.
Ubicumque occurrit multiplicitas proportionum, inter quas facile non reperitur proportio, censendum est multas earum irrationales esse ad invicem, quare et spatia pertransita irrationalia esse. Thomas 1509, S. 164.
Qua propter cum talis casus proponitur, respondendum est spatium pertransitum in tota hora incommensurabile esse spatio pertransito in prima parte proportionali. Thomas 1509, S. 164.
Respondeo, quod in simili negotio duplici cautela utendum censeo. Thomas 1509, S. 164.
Prima pro delubrio et ridiculo habeatur argumentum eius tanquam inutile et [non] intelligibile, petaturque calamus et atramentarium, ut specie multiplicationis ceterisque algorithmi speciebus calculari valeat velocitatis intensio in casu per eum posito. Thomas 1509, S. 164.
[...] dicatur breviter arguenti, quod talis velocitas non potest infallibiliter et certitudinaliter calculari perinde, atque multae aliae difformes velocitates non valent naturaliter ad uniformitatem reduci. Et si clamoribus velit respondentem expugnare oppositum asseverendo, proponat ei respondens similem casum et dicat ei, ut certificet illi de spatio pertransito adaequato mediante tali velocitate difformi. Et si dixerit, quod non est possibile naturaliter invenire velocitatem adaequatam in tali casu, subiungat respondens, quod nec in suo similiter pari ratione. Si autem dicat opponens se nolle tale spatium assignare, quavis assignabile sit naturaliter, hoc idem dicat ei respondens. Thomas 1509, S. 164.
Omnis motus uniformiter difformis quoad tempus mensurari habet penes gradum medium, omnisque difformiter difformis quoad tempus penes reductionem ad uniformitatem sive penes calculationem denominationis, et si in non nullis casibus, difficile sit aut impossibile naturaliter ad admissim infallibiliterque velocitatem mensurare. Thomas 1509, S. 164f.
[...] ad primam responsum est ibi usque ad ultimam replicam, ad quam respondeo concedendo sequelam et negando falsitatem consequentis, et cum probatur, quia alias sequeretur mobile, quod continuo infinite velociter intendit motum, suum infinite tarde moveri, nego illam sequelam et ad probationem admitto casum et ad argumentum concedo antecedens capiendo ly „infinita“ in maiore et minore syncathegorematice et nego consequentiam. Thomas 1509, S. 165.
[...] in casu posito quodlibet illorum immediate post hoc infinita tarditate movebitur, et tamen immediate post hoc infinita velocitate movebitur aliquod illorum. Thomas 1509, S. 165.
[...] in casu posito quodlibet istorum immediate post hoc in infinitum modicum spatium per aliquod tempus pertransibit, et tamen immediate post hoc infinite magnum spatium pertransibit aliquod illorum per aliquod tempus. Thomas 1509, S. 165.
[...] immediate post hoc infinita tarditate movebitur aliquod illorum, et nullum istorum immediate post hoc movebitur ita tarde sicut A, et A movebitur et ipsum A non immediate p[os]s hoc infinita tarditate movebitur. Thomas 1509, S. 165.
[...] ad quam respondeo negando sequelam immo dico, quod possibile est, quod aeque velociter geometrice intendatur unus motus in tempore finito, sicut alter remittitur ipsis in principio existentibus aequalibus, sed oportet illum, qui intenditur, infinitam velocitatem acquirere in illo tempore finito, in quo alter motus remittitur ad non gradum. Thomas 1509, S. 165.
[...] respondeo negando sequelam, immo dico, quod quando unus est remissus ad subduplum, alter est remissus ad non gradum. Thomas 1509, S. 165.
Et ratio est, quia illud mobile non sufficit ad illum motum remitti in duplo velocius altero, q[u]ia hic non loquimur de velocitate geometrica, sed arithmetica, quae debet attendi penes latitudinem deperditam et non penes proportionem deperditam, et sic debet semper capi, quando dicitur aeque velociter, si non addatur proportionabiliter aut geometrice. Thomas 1509, S. 165.
Thomas 1509, S. 165.
Ad quartam confirmationem responsum est usque ad ultimam replicam, ad quam respondet septima propositio primi notabilis huius quaestionis cum annotationibus ibi positis. Thomas 1509, S. 165.
Vgl. Thomas 1509, S. 165.
[...] immo dico, quod dabitur certa intensio in casu posito in argumento, sed non erit rationalis ad intensionem velocitatis primae partis. Thomas 1509, S. 165.
Vgl. Thomas 1509, S. 165.
Vgl. Thomas 1509, S. 165.
Quaeritur ergo, penes quod tanquam penes effectum motus difformis quoad tempus et subiectum simul necnon motus mixti velocitas attendi habeat, an videlicet motus difformis quoad tempus et subiectum simul velocitas mensurari debeat penes lineam descriptam mediante velocitate uniformi, ad quam talis velocitas difformis reduci habet, et an motus mixti velocitas attendi habeat penes spatium compositum ex spatiis pertransitis mediantibus pluribus motibus, quibus simul moveatur mobile motum motu mixti. Thomas 1509, S. 166. Das ist eine klassische Formulierung der Frage nach der Wirkung einer Bewegung. Vgl. Maier 1949, S. 111.
[...] velocitas motus difformis quoad tempus et subiectum simul non attendi habeat penes lineam descriptam et cetera. Thomas 1509, S. 166.
Quia si sic sequeretur, quod adaequata velocitas talis motus mensuranda esset penes reductionem ad uniformitatem, sed consequens est falsum. Thomas 1509, S. 166.
Et ratio est, quia illa rota movetur duplici motu per utrumque describendo spatium, puta motu circulari vel quodammodo habente naturam motus circularis, (quia continuo movetur super eodem axe, quamvis non proprie lineam circularem describat, ut superius dictum est,) et insuper movetur punctus, a cuius velocitate debet sumi totalis velocitas ipsius rotae motu rarefactionis continuo recedendo a centro. Quare velocitas illius puncti et ex consequenti ipsius rotae debet commensurari penes lineam aggregatam ex linea, quam describeret ille punctus seclusa rarefactione et penes lineam brevissimam, per quam plus distat a centro, quam ante rarefactionem distabat. Thomas 1509, S. 166
Sed contra, quia tunc sequeretur, quod si rota B inciperet moveri circulariter puncto eius medio, a cuius velocitate – ut suppono – debet commensurari totalis rotae velocitas movente in prima parte proportionali horae proporti[o]ne quadrupla divisae velocitate ut quatuor et in secunda in duplo velocius et in tertia in duplo velocius quam in secunda et sic consequenter, et cum hoc in qualibet parte proportionali illa rota uniformiter rarefieret taliter, quod ille punctus medius in qualibet parte proportionali acquireret pedalem distant[i]am a centro supra distantiam habitam, tunc ipsa rota in illa hora adaequate finite describeret ad lineam descriptam in prima parte proportionali, secundum consequens est falsum. Thomas 1509, S. 166.
[...] ergo sequitur, quod non pertransit in totali hora duplum spatium adaequate ad spatium per[t]ransitum in prima parte proportionali. Thomas 1509, S. 166.
[...] si illa pars esset vera, sequeretur, quod aliquod mobile in aliquo tempore continuo remitteret motum suum proprium usque ad non gradum, et tamen continuo in eodem tempore velocius et velocius spatium pertransiret, sed hoc videtur implicare, igitur illud, ex quo sequitur. Thomas 1509, S. 166.
[...] et pono, quod Socrates moveatur in aliqua navi versus eandem differentiam, versus quam movetur navis ab aliquo gradu conti[n]uo remittendo motum suum usque ad non gradum ipsa nave continuo intendente motum suum ab eodem gradu velocius, quam Socrates remittat. Quo posito Socrates continuo remittit motum suum et hoc usque ad non gradum, et tamen continuo in eodem tempore velocius et velocius spatium pertransit. Quod fuit probandum, igitur propositum. Maior patet ex casu, et minor probatur, quia continuo velocitas mixta sive composita ex velocitate propria, qua movetur Socrates, et ex velocitate ipsi[u]s navis est maior et maior, cum continuo maiorem velocitatem acquirit, quam deperdit ex casu, igitur continuo Socrates velocius et velocius spatium pertransit. Quod fuit probandum. Thomas 1509, S. 166
Sed contra, quia tunc sequeretur, quod staret in casu Socratem valde fatigari nitendo moveri nullo impedimento posito, immo ipso Socrate habente optimam dispositionem ad currendum et ad movendum, et tamen nullo pacto moveri, sed hoc est falsum. Thomas 1509, S. 167.
[...] nullus est motus mixtus. Thomas 1509, S. 167.
[...] si esset aliquis motus mixtus, maxime esset motus compositus ex ascensu et descensu, sed nullus est dabilis talis. Thomas 1509, S. 167.
[...] si aliquis talis esset dabilis, sequeretur, quod dabile esset unum corpus finitum, cuius una pars ascenderet, et alia descenderet, et relictum suae naturali dispositione sic perpetuo moveretur continuo una parte eius ascendente et alia descendente, sed consequens est falsum. Thomas 1509, S. 167.
[...] et pono casum, quod terra sit perforata per centrum mundi ab oriente in occidentem, et capiatur globus terrae uniformis gravitatis vel alicuius alterius figurae, (in idem reddit,) descendatque illa terra per illud foramen usque ad centrum mundi illo foramine vacuo existente, permittatque deus illam terram moveri tamdiu, quamdiu habuerit proportionem maioris inaequalitatis ad movendum. Thomas 1509, S. 167.
[...] in omni motu difformi quoad tempus et subiectum simul velocitas mensuranda est penes reductionem ad uniformitatem saltem denominationis. Thomas 1509, S. 167.
Hoc tamen unum advertendum est, quod motus difformis quoad tempus et subiectum simul aliquando fit secluso alio motu subiecti, puta rarefactionis aut condensationis et cetera, ut cum rota non rarefacta aut condensata continuo circulariter velocius et velocius movetur aut tardius et tardius. Aliquando vero fit talis motus concomitante rarefactione aut condensatione sive augmentatione et cetera. Primo modo debet mensurari talis motus velocitas penes velocitatem, qua movetur punctus medius aut velocissime motus secundum diversitatem opinion[]um eo modo, quo superius dicebatur de motu difformi quoad subiectum tantum. Et [...] mensuranda est velocitas illius motus penes lineam descriptam a puncto medio talis corporis vel velocissime moto, sed tale punctum duplici motu movetur, motu videlicet locali et rarefactionis sive condensationis et cetera. Et ideo tale punctum tantam lineam describit, ac si moveretur primo modo, et insuper describit illam lineam, per quam plus distat, si rarefiat, aut minus, si condensetur, a centro talis motus, quam antea distabat a principio motus. Thomas 1509, S. 167.
Hic tamen tu adverte, quod nonnumquam movetur aliquod mobile et motu recto e[t] circulari et rarefactionis simul, ita quod continuo centrum illius corporis moveatur, quemadmodum contingit, si pila vel aliquod aliud corpus sphaericum vel alterius figurae moveatur motu recto et circulari continuo rotando continuoque rarefiendo, et in hoc et simili casu velocitas talis mobilis iudicanda est penes velocitatem centri mobilis. Thomas 1509, S. 167.
Vgl. Thomas 1509, S. 168.
[...] secundum se et quodlibet sui moveatur de per se quolibet illorum motuum, et non aliquo illorum ad motum alterius, ut quando idem movetur simul motu locali et motu alterationis. Thomas 1509, S. 168.
Secundo modo dicitur aliquid moveri motu mixto ex pluribus motibus non aeque primo, sed uno motu ex se et alio ad motum alterius sic, quod unus illorum motuum sit illi mobili proprius, et alter non. Thomas 1509, S. 168.
Potest addi tertius modus, qui est, cum una pars ascendit et alia descendit. Thomas 1509, S. 168.
Unde velocitas talis motus debet attendi penes spatium interceptum inter punctum fixum et quiescens et punctum sive terminum, in quo est tale mobile in fine motus, hoc est penes lineam descriptam a tali mobili inter illos duos terminos. Thomas 1509, S. 168.
[...] possibile est ex duobus rectis motum circularem describere, id est, quod possibile est aliquid moveri duplici motu recto describendo circulum vel partes circuli. Thomas 1509, S. 168.
[...] ex duobus motibus rectis potest fieri unus motus mixtus in eodem tempore describens costam alicuius quadrati et diametrum eiusdem. Thomas 1509, S. 168.
Possibile est idem mobile moveri motu simplici, cuius quaelibet pars movetur motu mixto. Thomas 1509, S. 168.
Possibile est ex duobus motibus regul[ar]ibus fieri unum irregularem. Thomas 1509, S. 168. Unter regulären Bewegungen werden hier uniforme Bewegungen verstanden, irreguläre als ungleichförmige Bewegungen. Vgl. Thomas 1509, S. 168.
Tangendo materiam tertii argumenti, (cuius principalis inquisitio est, an terra, de qua fit mentio in casu eius, perpetuo sic moveretur, ita quod non posset relicta suae naturali dispositioni taliter moveri, quod centrum eius fiat centrum mundi,) quod teste philosopho primo de caelo et mundo idem est naturalis locus totius et partis. Thomas 1509, S. 168.
Inquit enim ad quemcumque locum natum est aliquid natura moveri, ad eundem natum est moveri quodlibet congeneae consimilisque naturae. Quare si aliqua terra esset in aere remoto impedimento, ipsa descenderet, quoad usque centrum eius efficeretur centrum mundi. Nec pars illius terrae resistit ipsi terrae, ne centrum eius fiat centrum mundi, quam idem est appetitus partis et totius, cuius est pars, ut satis naturaliter inducit calculator in capitulo de loco elementi. Thomas 1509, S. 168.
[...] videlicet quod perforata ipsa terra, ut ponitur in casu tertii argumenti, et descendente quadrato terreo, ut ibidem ponitur, si cum talis globus devenit ad centrum terrae, pars ultra centrum resisteret parti citra centrum, ne descenderet, perpetuo tale quadratum ibi moveretur ceteris impedimentis et adiumentis deductis. Thomas 1509, S. 168.
Tali quadrato sic descendente unaque parte eius minore medietate illius quadrati existente ultra centrum mundi, residua vero parte totius quadrati existente citra centrum mundi pars intercepta inter centrum mundi et centrum talis quadrati est medietas excessus, quo pars citra centrum mundi excedit partem existentem ultra centrum mundi. Thomas 1509, S. 168.
Quando inter aliquos terminos est proportio maioris inaequalitatis et maiore quartam excessus, quo minorem excedit, deperdente adaequate minoreque eandem dumtaxat quartam acquirente, quae a [maiore] deperditur, proportio inter datos terminos plusquam ad subduplum sui diminuitur, et ex consequenti data proportio ultra suam medietatem deperdit. Thomas 1509, S. 169.
[...] immediate post instans, quod est praesens, ascendet aliquid, immediate post illud descendet, et tamen nihil immediate post hoc ascendet, quod immediate post hoc descendet. Thomas 1509, S. 170.
Immediate post instans, quod est praesens, ascendet aliquid, quod praesens ascendet aliquid, quod immediate post idem instans descendet, et tamen non immediate post instans, quod est praesens, descendet aliquid, quod immediate post idem instans ascendet. Thomas 1509, S. 170.
Immediate post instans, quod est praesens, ascendet aliquid, quod immediate post idem instans, quod est praesens, descendet, et tamen nihil simul ascendet, et descendet adaequate divisive capiendo ly. Thomas 1509, S. 170.
Vgl. Thomas 1509, S. 170.
Commensuranda enim est utraque velocitas, et qua illud corpus movetur circulariter, et qua movetur motu rarefactionis puncto eius, a quo debet sumi velocitas totius motus continuo acquirente maiorem et maiorem distantiam a centro. Thomas 1509, S. 170.
[...] possibile est aliquod corpus circulare continuo uniformiter et aeque velociter moveri, et tamen ipsum continuo rarefieri et effici maius. Thomas 1509, S. 170.
[...] si aliqua rota in hora moveatur circulariter puncto medio semidiametri continuo motu circulari movente uniformiter, motu vero rarefactionis continuo intendente motum suum in qualibet parte proportionali horae proportione dupla, sequente in duplo velocius rarefiente quam in immediate praecedenti, tunc spatium descriptum a tali puncto est infinitum. Thomas 1509, S. 170.
Immo contra: motio navis est Socrati impedimento. Fatigatur tamen Socrates non per motum, quo describat aliquod spatium fixum, sed quia describit aliquod spatium non fixum, ad cuius descriptionem non sequitur Socratem proprie moveri. Manet enim Socrates in eodem loco fixo. Thomas 1509, S. 170.
[...] ita potest aliquod corp[]us disponi difformiter in partibus suis, quod ipsum in tempore finito movebitur, quousque centrum eius sit centrum mundi. Thomas 1509, S. 170f.
Et manifestum est, quod aliquod spatium sufficit pertransiri in medietate horae mediante velocitate nata provenire a proportione F, pono igitur, quod secunda pars proportionalis ipsius D partis diminuatur secundum dimensionem, secundum quam pertransit centrum mundi, quousque sit secundum illam dimensionem aequalis spatio nato pertransiri ab F proportione in medietate horae, ipsa tamen semper manente tanta, quanta erat antea, ita quod augeatur secundum aliam dimensionem. Et postquam secunda pars proportionalis D partis pertransit centrum mundi secundum se et quodlibet sui, signo proportionem, quae sit G, a qua debet quarta pars proportionalis descendere, quae est minor F, ut constat. Thomas 1509, S. 171.
Et manifestum est, quod aliquod spatium sufficit pertransiri in quarta parte horae mediante proportione, ergo pono igitur, quod tertia pars proportionalis D partis dim[i]nuatur secundum dimensionem, secundum quam pertransit centrum mundi, quousque secundum illam dimensionem sit aequalis spatio nato pertransiri a G proportione in quarta parte horae. Et sic fiat de qualibet sequente, quod ipsa videlicet diminuatur secundum dimensionem, secundum quam pertransit centrum mundi, quousque sit aequalis spatio nato pertransiri a proportione, a qua debet incipere pertransire centrum mundi pars immediate sequens, et hoc in tempore subduplo vel minori, quam sit tempus, in quo adaequate pars immediate praecedens pertransit centrum mundi, qualibet tamen continuo manente tanta, quanta erat antea, ita quod augeatur secundum aliam dimensionem. Thomas 1509, S. 171.
Tunc manifestum est, quod totum illud corpus, postquam prima pars D partis praeterivit centrum mundi, movebitur praecise per unam horam vel per minus tempus, ante quam centrum illius corporis fiat centrum mundi. Thomas 1509, S. 171.
Vgl. Thomas 1509, S. 171.
