Kapitel 1.1
Das erste Kapitel enthält die Definitionen des Begriffes Verhältnis und seiner Aufteilungen.
definitio der proportio:
„Jede Zahl und gleichsam jede Quantität, die zu einer anderen Zahl in Beziehung gesetzt wird, (wie Nikomachos sagt und Boëthius im ersten [Buch] der Arithmetik), ist entweder zu dieser [Zahl] gleich oder ungleich. Wenn sie [der anderen Zahl] gleich ist, stellt sie ein Verhältnis von Gleichheit [zwischen beiden] auf. Wenn sie aber [der anderen] ungleich [ist], ergibt sich aus ihr mit der anderen [Zahl] ein Verhältnis der Ungleichheit. Daher besteht ein Verhältnis aus zwei Zahlen oder zwei Quantitäten, [von denen] eine in Bezug auf die andere eine fest stehende Beziehung hat, wie die Beziehung, die zwischen Vier und 4 besteht, diejenige, die zwischen Zwei und Vier ist, oder die, die zwischen einem Fuß und zwei Fuß besteht. Denn Verhältnis ist eine Sammelbezeichnung, die für zwei Sachen oder vielmehr irgendwie viele oder mehrere Sachen annimmt, dass sie durch das Nebeneinanderschreiben gleich seien, oder dass die eine [Zahl] die andere [Zahl] um einen Überhang überträfe.“1
Einschränkung: „Daher gilt diese Schlussfolgerung nichts: Dieses Verhältnis stellt [genau] ein Verhältnis dar, also ist sie ein Seiendes. Weil sich – wie gezeigt – eine ein Fuß [lange Strecke] und eine zwei Fuß [lange Strecke] nicht als ein Einziges von ihnen konstituieren, ist es wahr zu sagen, dass sie sich in einem gewissen Verhältnis befinden, nämlich einem doppelten [Verhältnis]. Dennoch sind diese zwei [Zahlen] nicht ein Seiendes.“2
Aber es gilt: „Jedoch ist ein Verhältnis [etwas] Zweifaches: Daher gibt es ein gewisses Verhältnis der Gleichheit, ein anderes aber [ein Verhältnis] der Ungleichheit.“3
definitio der proportio aequalitatis:
„Das Verhältnis der Gleichheit ist eine Beziehung zweier gleicher Quantitäten oder Zahlen wie die Beziehung, die zwischen 8 und 8 oder zwischen einer ein Fuß [langen Strecke] und einer [anderen] ein Fuß [langen Strecke] ist. Und hier kann sowohl für eine Quantität an Last wie für eine Quantität an virtus als eine Quantität angenommen werden, wie es der selige Augustinus im fünften [Buch] über die Dreifaltigkeit auffasst.“4
1. Teil der definitio der proportio inaequalitatis:
„Aber ein Verhältnis der Ungleichheit ist eine fest stehende Beziehung zweier Quantitäten oder Zahlen, die der einen [Quantität oder Zahl] zur anderen [Quantität oder Zahl] wie das Verhältnis, das zwischen 2 und Vier besteht [oder das zwischen] einer ein Fuß [langen Strecke] und einer zwei Fuß [langen Strecke besteht]. Ebenso gilt von den Verhältnissen der Ungleichheit: Einige sind [ein Verhältnis] größerer Ungleichheit, einige [andere] aber [ein Verhältnis] kleinerer [Ungleichheit].“5
definitio der proportio maioris inaequalitatis: „Ein Verhältnis größerer Ungleichheit ist eine Beziehung einer größeren Quantität zu einer kleineren [Quantität] wie die Beziehung, die zwischen Vier und Zwei besteht.“6
definitio der proportio minoris inaequalitatis: „Aber ein Verhältnis kleinerer Ungleichheit ist eine Beziehung einer kleineren Quantität zu einer größeren [Quantität], wie die Beziehung der Zwei zur 4.“7
Korollar: „Daraus folgt, dass diese zwei Bezeichnungen „Verhältnis größerer Ungleichheit“ und „Verhältnis von kleinerer Ungleichheit“ für ein und dasselbe stehen. Dennoch kennzeichnet die Bezeichnung „Verhältnis größerer Ungleichheit“ etwas, bei dem die größere Zahl die kleinere [Zahl] übertrifft. Und folgerichtig kennzeichnet die Bezeichnung „Verhältnis kleinerer Ungleichheit“ etwas, bei dem die in Hinsicht auf die Anzahl oder auf die Quantität kleinere [Zahl oder Quantität] von der größeren [Zahl oder Quantität] übertroffen wird. Und wenn dennoch so ein Verhältnis von größerer Ungleichheit nicht als eine Aggregatum aus Zahlen aufgefasst wird, die ein Verhältnis der Ungleichheit haben, sondern als eine größere Zahl, wird demzufolge ein Verhältnis kleinerer Ungleichheit auch als eine kleinere [Zahl aufgefasst]. Und auf diese Art und Weise sind die Bezeichnungen umkehrbar. Denn indem man es auf diese Weise auffasst, wenn man [zum Beispiel] 8 mit 4 vergleicht, sind die 8 ein Verhältnis der größeren Ungleichheit und die 4 [ein Verhältnis] der kleineren Ungleichheit.“8
2. Teil der definitio der proportio inaequalitatis:
„Ebenso ist ein Verhältnis der Ungleichheit [etwas] Zweifaches, weil manche [Zahlen oder Quantitäten] rational sind und manche irrational.“9
definitio der proportio inaequalitatis rationalis:
„Ein rationales Verhältnis ist jenes Verhältnis, das unmittelbar von einer fest stehenden Zahl oder einem Bruch von Zahlen benannt wird wie zum Beispiel das doppelte [Verhältnis] oder das eineinhalbfache [Verhältnis] und so weiter. Auf andere Art und Weise besteht das rationale Verhältnis aus zwei Quantitäten, die sich folgendermaßen verhalten: Dieselbe [Zahl oder Quantität] ist der irgendwievielte Teil der anderen der beiden [Zahlen oder Quantitäten]. In einem wohlwollenden Sinne sage ich dasselbe.“10
Korollar mit der definitio des pars aliquota: „Daraus folgt, dass ein rationales Verhältnis aus einer beliebigen Zahl in Bezug zu einer anderen beliebigen Zahl besteht, weil ja die Eins einer beliebigen Zahl der irgendwievielte Teil [der anderen Zahl] ist. Daher ist jene [Zahl] der irgendwievielte Teil, die irgendwieviel Mal zusammengenommen genau sein Ganzes wieder ergibt, wie die Eins der irgendwievielte Teil der Zahl Vier ist, da ja die Eins dreimal genommen der Drei gleichgestellt ist und viermal genommen der Vier. Und die Zwei ist der irgendwievielte Teil der Zahl Acht, weil ja die Zwei genau viermal genommen die Zahl Acht aufstellt. Daher ist es offenbar, dass die Zwei nicht der irgendwievielte Teil der Zahl Sieben ist, weil sie ja irgendwievielmal [auch] genommen nicht genau das Ganze ergibt.“11
definitio der proportio inaequalitatis irrationalis:
„Jedoch als irrational gilt jenes Verhältnis, das nicht unmittelbar von irgendeiner Zahl bestimmt werden kann. Auf andere Art und Weise besteht das irrationale Verhältnis aus zwei Quantitäten, die sich folgendermaßen verhalten: Kein irgendwievielter Teil der einen [Zahl oder Quantität] ist der irgendwievielte Teil der anderen [Zahl oder Quantität] wie das Verhältnis, das zwischen der Diagonalen und der Seite [eines] Vierecks besteht. Denn die Diagonale übertrifft die Seite nicht um irgendwievielmal und nicht um irgendeinen Teil irgendwievielmal, noch um irgendwie viele Teile irgendwievielmal, wie weiter unten bewiesen werden wird im Kapitel über das irrationale Verhältnis.“12
species proportionum rationalium:
„Es gibt fünf species der rationalen Verhältnisse, drei einfache und zwei zusammengesetzte [Verhältnisse]. Das sind die drei einfachen [Verhältnisse]: Das vielfache [Verhältnis], das superpartikulare [Verhältnis] und das suprapartiente [Verhältnis]. Die zusammengesetzten [Verhältnisse] sind aber [immer] vielfältig: Das vielfältig superpartikulare [Verhältnis] und das vielfältig suprapartiente [Verhältnis].“13
proportio mulitplex: „Daher ist das vielfältige Verhältnis ein Verhältnis, in dem die größere [Zahl] eine kleinere [Zahl] irgendwievielmal nur innehält, wie das Doppelte oder das Dreifache oder die 4. Denn sie beinhaltet die 2 zweimal. Und die 6 beinhaltet die 2 eben dreimal. Und daher ist zwischen jenen ein vielfältiges Verhältnis.“14
proportio superparticularis: „Das superpartikulares Verhältnis ist ein Verhältnis, in dem die größere [Zahl] die kleinere [Zahl] nur einmal beinhaltet und genau irgendeinen irgendwievielten Teil von ihr wie das Verhältnis sechs zu 4. Denn 6 beinhaltet die 4 nur einmal und [ihre] Hälfte, die ein irgendwievielter Teil derselben 4 ist.“15
proportio suprapartiens: „Das suprapartiente Verhältnis ist aber ein Verhältnis, in dem die größere [Zahl] eine kleinere [Zahl] nur einmal beinhaltet und irgendwie viele irgendwievielte Teile von ihr. Diese machen zugleich keinen einzelnen irgendwievielten Teil von ihr aus, wie das Verhältnis, das zwischen 7 und 5 besteht. Denn die 7 beinhaltet nur einmal die 5 und zwei irgendwievielte Teile von ihr, nämlich zwei Einsen.“16
proportio multiplex superparticularis: „Aber das vielfältig superpartikulare Verhältnis ist jenes [Verhältnis], in dem die größere [Zahl] eine kleinere [Zahl] irgendwievielmal beinhaltet und dazu nur irgendeinen irgendwievielsten Teil von ihr wie das Verhältnis, das zwischen Neun und 4 besteht. Denn die 9 beinhaltet die 4 zweimal und einen Teil der Zahl Vier, nämlich die Eins.“17
proportio multiplex suprapartiens: „Das vielfältig suprapartiente Verhältnis aber ist jenes [Verhältnis], in dem die größere [Zahl] eine kleinere [Zahl] irgendwievielmal innehält und irgendwie viele irgendwievielte Teile von ihr. Diese [Teile] machen nicht [nur] einen irgendwievielten Teil von ihr aus wie das Verhältnis, das zwischen 11 und 4 besteht. Denn 11 beinhaltet die 4 zweimal und drei irgendwievielte Teile von derselben 4. Und jene [Teile] machen nicht einen irgendwievielten Teil derselben 4 aus.“18
ratio proportionum rationalium des Albertus von Sachsen: „Die Hinlänglichkeiten dieser Verhältnisse bzw. der species der Verhältnisse können so durch eine ratio erachtet werden, wie es Albertus von Sachsen in seiner Abhandlung über die Verhältnisse gemäß anderen Mathematikern anführt: Jede Zahl oder Quantität, die in Bezug auf eine andere Quantität ein rationales Verhältnis hat, übertrifft sie entweder diese oder wird von ihr übertroffen. Wenn sie sie übertrifft, beinhaltet sie dieselbe entweder irgendwievielmal oder nur einmal und irgendetwas darüber oder mehrere Male und etwas darüber. Wenn die erste [Möglichkeit vorliegt], dann wird es ein vielfältiges Verhältnis sein. Wenn die zweite [Möglichkeit vorliegt], ist dieses „irgendetwas darüber“ entweder genau ein irgendwievielter Teil von ihr sein oder mehrere irgendwievielte Teile, die nicht einen irgendwievielten Teil ausmachen. Wenn die erste [Möglichkeit der zweiten Möglichkeit vorliegt], so ist es ein superpartikulares Verhältnis. Wenn die zweite [Möglichkeit der zweiten Möglichkeit vorliegt], [dann] ist es ein suprapartientes Verhältnis. Wenn aber eine größere Quantität eine kleinere [Quantität] mehrmals innehält und irgendetwas darüber, ist das etwas, was es darüber beinhaltet, genau ein irgendwievielten Teil oder mehreren irgendwievielten Teil, die nicht einen [irgendwievielten Teil] ausmachen. Wenn es die erste [Möglichkeit] ist, so ist es ein vielfältig superpartikulares Verhältnis. Wenn die zweite [Möglichkeit vorliegt], so ist es ein vielfältig suprapartientes Verhältnis. Und daher kann die größere Quantität, die ein rationales Verhältnis zu einer kleineren Quantität hat, nicht auf mehrfache Art und Weise auf jene [kleinere Quantität] zurückgeführt oder [mit ihr] verglichen werden als auf diese fünf Art und Weisen. Der Nachsatz lautet: Es gibt nicht mehr Arten eines rationalen Verhältnisses als diese 5, da man nämlich [auch] auf diese Art und Weise die Hinlänglichkeiten der Verhältnisse kleinerer Ungleichheit verfolgen kann. Allein durch den Verstand unterscheiden sich die Verhältnisse größeren Ungleichheit und [die Verhältnisse] kleineren [Ungleichheit].“19
Kapitel 1.2
Das zweite Kapitel widmet sich der Generierung von Verhältnissen. Es beginnt mit folgender These: „Jedes Verhältnis oder jede Klasse eines Verhältnisses hat unendliche species.“20
Zu den species des genus der proportio multiplex:
„Daher hat die Klasse des vielfältigen [Verhältnisses] unendliche species, die von einer natürlichen Reihe an Zahlen bestimmt sind, nämlich das doppeltes [Verhältnis], das von der Zwei denominiert wird, das dreifaches [Verhältnis], [das] von der Drei [denominiert wird], das tausendfache [Verhältnis], [das] von der Tausend [denominert wird], und das hundertfache [Verhältnis], [das] von der Hundert [denominiert wird] und so ins Unendliche.“21 Und weiter: „Denn jenes Verhältnis ist doppelt, in dem die größere [Zahl] die kleinere [Zahl] genau zweimal enthält wie 4 und 2. Und ein dreifaches [Verhältnis] ist dasjenige [Verhältnis], in dem die größere [Zahl] die kleinere [Zahl] genau dreimal enthält, und ein vierfaches [Verhältnis besteht, wenn die größere Zahl die kleinere Zahl] genau viermal [enthält] und so ins Unendliche.“22
Zu den proportiones duplae und deren generatio:
„Erzeugt werden aber alle doppelten Verhältnisse, die unendlich sind, auf folgende Art und Weise: Zuerst wird eine natürliche Reihe an Zahlen in einer Linie aufgestellt, und auf einer anderen, darunter liegenden Linie werden alle Zahlen aufgestellt, die sie um das Zweifache bis ins Unendliche übertreffen, wobei von der 2 werden sollte. Und indem die erste [Zahl] der oberen Linie mit der ersten [Zahl] der unteren Linie verglichen wird, und die zweite [Zahl] mit der zweiten [Zahl verglichen wird], und die dritte [Zahl] mit der dritten [Zahl verglichen wird] und so bis ins Unendliche, werden auf diese Art und Weise [die Zahlen] eines unendlichen doppelten Verhältnisses gefunden werden. In der vorliegenden Figur kann man das deutlich erblicken. Man nehme von einer natürlichen Reihe an Zahlen die Ordnung der Zahlen an, wobei von der Eins an begonnen werden muss und keine Zahl ausgelassen werden darf, wie 1, 2, 3, 4 und so weiter.“23

Abb. 1: Alvarus Thomas, Liber de triplici motu, S. 4.
Zur generatio der proportiones triplae:
„Unendliche dreifache Verhältnisse werden auf folgende Art und Weise erzeugt: Alle Zahlen werden in einer natürlichen Reihe an Zahlen gemäß aufgestellt. Und es muss mit der Eins angefangen werden in der einen Linie. Und auf einer darunter liegenden Linie werden alle Zahlen aufgestellt, die [die Zahlen der oberen Linie] dreifach übertreffen. Und dann muss die erste [Zahl] der unteren Ordnung mit der ersten [Zahl] der oberen [Ordnung] verglichen werden, und die zweite [Zahl] mit der zweiten [Zahl] und die dritte [Zahl] mit der dritten [Zahl]. Und so wird man unendliche dreifache Verhältnisse erhalten.“24
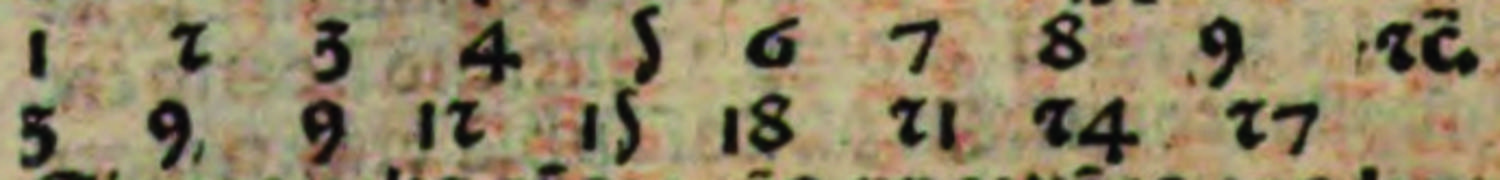
Abb. 2: Alvarus Thomas, Liber de triplici motu, S. 4.
Zur generatio von proportiones quadruplae, quintuplae et sextuplae:
„Wenn man aber alle vierfachen Verhältnisse erzeugen will, erfasse man die Zahlen, die sich um das Vierfache übertreffen, wobei von der Zahl Vier in einer natürlichen Reihe an Zahlen angefangen werden sollte. Wenn [man] aber [alle] fünffachen [Verhältnisse erzeugen will], erfasse man alle [Zahlen], die sich um das Fünffache übertreffen; für ein sechsfaches [Verhältnis erfasse man alle Zahlen], die [sich] um das Sechsfache [übertreffen]; und derart bis ins Unendliche, wie es leicht in den folgenden Bildern zu sehen ist.“25

Abb. 3: Alvarus Thomas, Liber de triplici motu, S. 4.
Zur Benennung von proportiones superparticulares:
„Ein superpartikulares Verhältnis aber hat unendliche species, die von den irgendwievielten Teilen und der Eins bestimmt werden, nämlich von der Hälfte, von einem Drittel, Viertel, Fünftel und so bis ins Unendliche. Und daher wird ihre erste und größte species einundeinhalbfach [oder auf Latein sesquialtera] genannt, und die zweite [species] aber einundeindrittelfach [oder auf Latein „sesquitertia“], [die dritte species] einundeinviertelfach [oder auf Latein „sesquiquarta“] , [die vierte species] einundeinfünftelfach [oder auf Latein „sesquiquinta“] und derart bis ins Unendliche. Daher bedeutet ,sesqui‘ so viel wie ein Ganzes. Und das ,altera‘ bedeutet soviel wie eine Hälfte, und daher ist ein einundeinhalbfaches Verhältnis [ein Verhältnis], in dem die größere [Zahl] die kleinere [Zahl] nur einmal und ihre Hälfte beinhaltet. ,Sesquitertia‘ ist daher [ein Verhältnis], in dem die größere [Zahl] die kleinere [Zahl] nur einmal beinhaltet und ein Drittel von ihr. Und ,sesquiquarta‘ [ist ein Verhältnis], in dem die größere [Zahl] die kleinere [Zahl] nur einmal beinhaltet und ein Viertel von ihr und derart bis ins Unendliche.“26
Zur generatio von proportiones superparticulares:
„Erzeugt werden dann die species dieses Verhältnisses auf folgende Art und Weise: Man nehme eine natürliche Ordnung an Zahlen, und man muss von der Zwei an beginnen, und man vergleiche die zweite [Zahl] mit der ersten [Zahl], und die dritte [Zahl] mit der zweiten [Zahl], und die vierte [Zahl] mit der dritten [Zahl] und derart bis ins Unendliche. Und [so] wird man alle species dieses Verhältnisses nach Art einer Reihe erhalten. Wenn man aber lieber unendliche einundeinhalbe [Verhältnisse] schaffen möchte, wird man alle Zahlen, die sich um das Zweifache übersteigen, in einer Linie aufreihen und in einer anderen alle Zahlen, die sich um das Dreifache übersteigen. Und dann würde man die erste [Zahl] der unteren [Linie] mit der ersten [Zahl] der oberen [Linie] vergleichen, und die zweite [Zahl] mit der zweiten [Zahl] und derart bis ins Unendliche. Wenn aber alle Zahlen, die sich um das Dreifache übersteigen, in eine Ordnung gestellt werden würden, und in eine andere [Ordnung alle Zahlen], die sich um das Vierfache übersteigen, wird eine zweite species geschaffen werden, nämlich die [species] des Einundeindrittel[verhältnisses]. Wenn man aber alle [Zahlen], die sich um das Vierfache übersteigen, in einer [Reihe] aufstellen würde, und in einer anderen [Ordnung alle Zahlen, die sich] um das Fünffache [übersteigen würden], wird man eine dritte species erschaffen, nämlich die [species] des Einundeinviertel[verhältnis], und so bis ins Unendliche in Hinsicht auf die anderen species, wie es in den folgenden Figuren offensichtlich ist.“27

Abb. 4: Alvarus Thomas, Liber de triplici motu, S. 5.
Zur Benennung der proportiones suprapartientes:
„Ein suprapartientes Verhältnis hat unendliche species, zum Beispiel ein einundzweidrittelfaches [Verhältnis] oder ein einundzweifünftelfaches [Verhältnis] oder ein einunddreiviertelfaches [Verhältnis] und so bis ins Unendliche. Daher ist ein Einundzweidrittelverhältnis [ein Verhältnis oder latinisiert ein suprabipartientes Drittelverhältnis], in dem die größere [Zahl] die kleinere [Zahl] nur einmal beinhaltet und zwei Drittel der kleineren [Zahl]. Daher werden bei einer beliebigen Benennung dieser species zwei Zahlen gestellt. Die erste Zahl bezeichnet die Zahl der irgendwievielten Teile. Und die zweite [Zahl] bezeichnet die denominationes derselben [Teile], wie [zum Beispiel] wenn wir Einundzweidrittel sagen. Das [Kennzeichen] „bi“ benennt die Anzahl der beliebigen Teile, von denen es [in diesem Fall] aussagt, dass es zwei sind. Und das [Kennzeichen] „tertias“ besagt, dass es drei Teile der kleineren Zahl gibt. Und so zeige es bei anderen auf!“28
Zur generatio der proportiones suprapartientes:
„Unendliche species dieses Verhältnisses werden aber auf diese Art und Weise erzeugt. Eine natürliche Ordnung an Zahlen werde in einer Reihe erfasst, wobei mit einer Drei angefangen werden muss, und in einer anderen [Reihe erfasse man] alle ungeraden Zahlen, wobei mit einer Fünf begonnen werden muss. Und man vergleiche die erste [Zahl] der ersten Reihe mit der ersten [Zahl] der anderen [Reihe] zusammen, und die zweite [Zahl] mit der zweiten [Zahl] und so ins Unendliche, und man wird eine unendliche species dieses Verhältnisses erhalten, wie es in dieser Darstellung offenbar ist.“29

Abb. 5: Alvarus Thomas, Liber de triplici motu, S. 5.
Zur generatio der proportiones multiplices superparticulares:
„Ein vielfach suprapartientes Verhältnis wird viele species haben, zum Beispiel das Fünfhalbefache, das Siebendrittelfache, Siebenhalbefache, das Zehndrittelfache und so bis in Unendliche. Die Definitionen der species sind aus dem Gesagten offensichtlich. Erzeugt werden aber unendliche species dieser [Art von Verhältnissen] auf folgende Art und Weise: Man erfasse in einer Ordnung eine natürliche Reihe Zahlen, wobei mit der Zwei angefangen werden muss. Und in einer anderen Ordnung erfasse man alle Zahlen, die sich um Fünf übertreffen, wobei mit der Fünf begonnen werden muss. Und [dann] muss die erste [Zahl] der ersten Ordnung mit der ersten [Zahl] der anderen [Ordnung] zusammengefasst werden. Dann wird die erste species festgelegt werden. Und [dann] muss die zweite [Zahl] die zweite [Zahl] bezogen werden, und [so] wird die zweite [species] ausgeführt werden, und so bis ins Unendliche, wie in der Figur offensichtlich ist.“30

Abb. 6: Alvarus Thomas, Liber de triplici motu, S. 5.
Zur generatio von infinitae proportiones multiplices superparticulares:
„Ein vielfach superpartikulares Verhältnis hat unendliche species, von denen jede beliebige species auch bis ins Unendliche [weiter] aufgeteilt wird; zum Beispiel die doppelt superpartikulare [species], die dreifach superpartikulare [species], die vierfach superpartikulare [species] und derart bis ins Unendliche. Um daher doppelt unendliche superpartikulare [species von Verhältnissen] zu erschaffen, werden zwei Reihen an Zahlen erfasst. Und in die erste [Reihe] wird eine natürliche Reihe an Zahlen gestellt werden und es muss mit der 2 angefangen werden. Und in die andere [Reihe] werden aber alle ungleichen Zahlen gestellt, und es muss mit der Fünf angefangen werden. Und dann muss die erste [Zahl] der unteren [Reihe] mit der ersten [Zahl] der oberen [Reihe] in Beziehung gesetzt werden, und die zweite [Zahl] der unteren [Reihe] mit der zweiten [Zahl] der oberen [Reihe] und folgerichtig so weiter. So wird man unendliche species dieses doppelten superpartikularen Verhältnisses erhalten. Um aber unendliche dreifach superpartikulare [species] zu erschaffen, stellt man in die erste Reihe eine natürliche Ordnung an Zahlen außer der Eins und in der zweiten [Reihe] werden alle Zahlen erfasst, die sich um Drei übersteigen. Es muss mit der Sieben angefangen werden. Und dann – dieses Verfahren wurde schon häufiger besprochen – müssen die Zahlen in Beziehung gesetzt werden. Und man wird unendliche dreifache superpartikulare Verhältnisse erhalten. Um aber unendliche vierfach superpartikulare [species] zu erzeugen, stellt man eine natürliche Reihe an Zahlen auf. Angefangen werden muss von der ersten Zahl in der oberen Linie.31 In die untere [Reihe] aber sollte man eine gewisse Reihe an Zahlen anordnen, die sich um Vier übersteigen, wobei mit der Neun angefangen wird. Um aber die darauf folgende species zu erzeugen, nämlich die fünffach superpartikularen [species], erfasse man für die erste Ordnung eine natürliche Reihe an Zahlen, wie man sie für eine beliebige species erfassen sollte. Und für die zweite [Ordnung nehme man] alle Zahlen, die sich um Fünf übersteigen, wobei mit der Elf angefangen werden muss. Und für eine darauf folgende species, wie nämlich für die sechsfach superpartikulares [species] erfasse man alle Zahlen, die sich um Sechs übersteigen, wobei man mit der Zahl Dreizehn anfangen muss. Für eine weitere [species nehme man alle], die sich um Sieben übersteigen, wobei mit der Fünfzehn angefangen werden muss und so bis ins Unendliche, wie es in den folgenden Figuren offensichtlich ist.“32

Abb. 7: Alvarus Thomas, Liber de triplici motu, S. 5.
Zur generatio der proportiones multiplices suprapartientes:
„Ein vielfach suprapartientes Verhältnis hat unendliche species, wie das Achtdrittelfache und das Elfdrittelfache und so bis ins Unendliche, indem man alle species eines vielfachen Verhältnisses mit einem beliebigen suprapartienten [Verhältnis] vereinigt und umgekehrt. Dann hat [das Verhältnis] gleichsam unendliche species, von denen eine beliebiges [species] sogar noch in unendliche [weitere] species geteilt werden kann, wie z.B. eine doppelt suprapartientes [species] in ein Achtdrittelverhältnis, in ein zwölffünftelfaches [Verhältnis und] in ein zehnviertelfaches [Verhältnis] und so bis in das Unendliche. Erzeugt wird eine doppelt suprapartientes [species] auf diese Art und Weise: Man stellt eine natürliche Reihe an Zahlen auf, wobei mit der Drei angefangen werden muss. Diese [Reihe] muss in einer solchen beliebigen species immer die erste sein. Und in einer Linie darunter werden alle Zahlen aufgestellt, die sich um Drei übersteigen, und es muss mit der Acht angefangen werden. Für die Erzeugung einer dreifach suprapartienten [species] werden in die zweite Reihe alle Zahlen gestellt, die sich um Vier übersteigen, und es muss von der Elf angefangen werden. Oder für die Erzeugung einer vierfach suprapartienten [species] werden in die zweite Reihe alle Zahlen gestellt, die sich um Fünf übersteigen, wobei angefangen mit der Vierzehn wird. Und für die folgenden species erfasse man alle [Zahlen], die sich um Sechs übersteigen, und für die nächstfolgende [species erfasse man alle Zahlen, die sich] um Sieben [übersteigen], und so weiter bis ins Unendliche, wie es in den folgenden Figuren offensichtlich ist.“33

Abb. 8: Alvarus Thomas, Liber de triplici motu, S. 5.
Kapitel 1.3
Das dritte Kapitel behandelt die Darstellung irrationaler Verhältnisse. Dazu werden zuerst sechs suppositiones aufgestellt. Aus diesen suppositiones leitet Alvarus Thomas dann vier conclusiones ab.
Die suppositiones
1. suppositio:
„Das Verhältnis der Quadratflächen ist das verdoppelte Verhältnis der Seiten. Dies bedeutet, wenn zwischen den Seiten zweier Quadratflächen irgendein Verhältnis von größerer Ungleichheit besteht, wird zwischen den Quadraten wird ein doppeltes Verhältnis zu dem [Verhältnis] bestehen, das zwischen den Seiten der ausgezeichneten Quadrate besteht. Wenn zum Beispiel zwischen den Seiten zweier ungleicher Flächenquadrate ein doppeltes Verhältnis wäre, würde zwischen den Quadraten ein vierfaches Verhältnis sein.“34 Das zu beweisen, verschiebt Alvarus Thomas auf ein späteres Kapitel (3.2.2).35
2. suppositio:
„Das Quadrat der Diagonalen verhält sich zum Quadrat der Seite in einem doppelten Verhältnis. Das bedeutet, dass ein Quadrat, von dem eine beliebigen Seite gleich der Diagonalen des anderen Quadrats ist, sich in einem doppelten Verhältnis zu jenem Quadrat verhält.“36
probatio: „Diese suppositio wird [folgendermaßen] bewiesen: Es gäbe ein großes Quadrat, dessen Seite sei DC und die Diagonale sei AC. Und es gäbe ein anderes kleines [Quadrat], das mit diesem in Verbindung steht. Dessen Seite sei CF und die Diagonale sei DC. Dann teilt man das größere Quadrat durch die zwei Diagonalen in vier gleiche Dreiecke, wie es in dieser Figur offensichtlich ist. So aufgestellt kann man [folgendermaßen] argumentieren: Das große Quadrat ist in Bezug auf das kleine Quadrat doppelt und das große Quadrat selbst ist das Quadrat der Diagonalen eben des kleinen Quadrats, wie es daher deutlich sichtbar ist. Daher verhält sich das Quadrat der Diagonalen in Bezug auf das Quadrat der Seite in doppeltem Verhältnis. Die Schlussfolgerung ist offensichtlich mit dem Vordersatz. Und der Nachsatz wird [so] argumentiert: Das größere Quadrat enthält genau viermal die Hälfte des kleineren Quadrats. Das große Quadrat selbst beinhaltet daher das kleine Quadrat genau zweimal. Die Schlußfolgerung ist daraus offensichtlich, und das Vordersatz wird bewiesen: Das große Quadrat beinhaltet genau viermal so viel, wie es das Dreieck DEC ist. Das ist offensichtlich. Und jenes Dreieck ist die Hälfte des kleinen Quadrats, wie es in der Figur dargestellt offensichtlich ist. Daher beinhaltet das große Quadrat genau viermal die Hälfte des kleinen [Quadrats]. Was zu beweisen war.“37
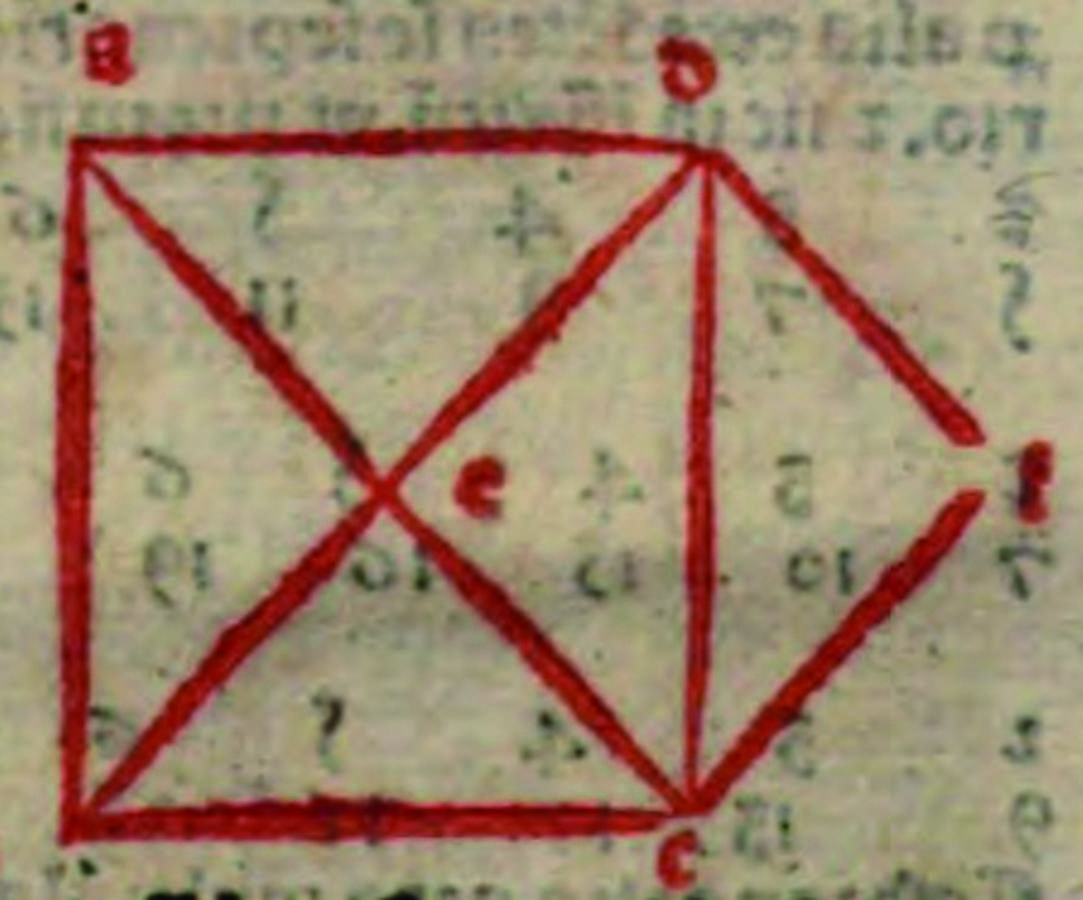
Abb. 9: Alvarus Thomas, Liber de triplici motu, S. 6.
3. suppositio:
„Es gibt ein Verhältnis der Diagonalen zur Seite, das die Hälfte eines doppelten [Verhältnisses] ist. Das wird bewiesen, weil das Verhältnis des Quadrats der Diagonalen zum Quadrat der Seite ein doppeltes [Verhältnis] ist, wie es aus der zweiten suppositio heraus offensichtlich ist. Daher ist das Verhältnis der Diagonalen zur Seite ein durch 2 geteiltes Verhältnis in Bezug auf das doppelte [Verhältnis] und folgerichtig die Hälfte des doppelten [Verhältnisses].“38
4. suppositio, in der die primi numeri speciei proportionum definiert werden:
„Von einem beliebigen suprapartienten Verhältnisses ist eine der Primzahlen ungerade. Die Primzahlen irgendeines Verhältnisses sind diejenigen, die in diesem Verhältnis Zahlen sind, wie z.B. Drei und Zwei sind die Erstzahlen eines anderthalbfachen Verhältnisses, weil in einer natürlichen Reihe an Zahlen ein anderthalbfaches Verhältnis zwischen keinen kleineren [Zahlen] gefunden wird.“39 Dann beweist Alvarus Thomas, dass eine Zahl der Erstzahlen bei jeder species proportionum ungerade sein muss, weil man beide Zahlen sonst weiter durch Zwei teilen könnte, bis eine oder beide Zahlen des Verhältnisses ungerade sind. Beispielsweise sind 3 und 2 die Erstzahlen eines anderthalbfachen Verhältnisses, aber nicht 6 und 4.40
5. suppositio:
„Jedes Quadrat einer ungeraden Zahl ist ungerade.“41 Den Beweis nimmt er aus dem zweiten Buch der Arithmetik von Nikomachus.42
6. suppositio:
„Keine ungerade Zahl ist das Doppelte zu irgendeiner anderen Zahl.“43
Die conclusiones
1. conclusio:
„Kein Verhältnis einer Diagonalen zu einer Seite ist vielfältig, vielfältig superpartikular oder vielfältig suprapartient.“44
2. conclusio:
„Kein Verhältnis einer Diagonalen zu einer Seite ist irgendein superpartikulares Verhältnis.“45
3. conclusio:
„Kein Verhältnis einer Diagonalen zu einer Seite ist irgendein suprapartientes Verhältnis.“46 Und weiter heißt es: „Dass sich irgendeine Quantität wie eine ungerade Zahl in Bezug zu einer anderen [Zahl] verhält, bedeutet, selbst – wenigstens in Bezug auf die Vorstellung – in gleiche Teile geteilt werden, die von einer ungeraden Zahl bestimmt wurden, wie bei drei Dritteln, fünf Fünfteln, sieben Siebenteln und so weiter, und zwar in Bezug auf die andere Quantität, die in zu ihnen [selbst] gleiche Teile geteilt wurde. Zum Beispiel, wenn ein Fuß in drei Drittel geteilt werden würde, zwei Fuß in sechs Sechstel und ein beliebiges dieser Sechstel gleich einem Drittel des einen Fußes ist, dann sage ich, dass ein Fuß sich wie eine ungerade Zahl in Bezug auf die zwei Fuß verhält. Man entgegne dennoch, dass es sein kann, dass er (der Fuß) sich in Bezug auf die zwei Fuß sich wie eine gerade Zahl verhalte. Dennoch wird das Verhältnis zwischen einem Fuß und zwei Fuß immer ein doppeltes [Verhältnis] sein. Die Diagonale aber und die Seite können sich niemals so verhalten, dass die Diagonale sich wie eine ungerade Zahl verhalte in Bezug auf die Seite oder umgekehrt, wie es bewiesen worden ist.“47
4. conclusio:
„Jedes Verhältnis einer Diagonalen zu einer Seite ist irrational.“48
Kapitel 1.4
Im vierten Kapitel beschäftigt sich Alvarus Thomas mit den species der irrationalen Verhältnisse und deren Generierung. Es heißt: „Das irrationale Verhältnis und ebenso das rationale [Verhältnis] werden in unendliche species unterschieden.“49 Zuerst werden suppositiones werden aufgestellt. Aus diesen suppositiones leitet Alvarus Thomas zwei conclusiones ab.
Die suppositiones
1. suppositio:
„Wenn sich zwei Quantitäten zueinander verhalten wie zwei Zahlen, verhält sich ein Aggregatum aus ihnen wie eine Zahl. Das wird bewiesen, weil sich immer aus der Anfügung der einen Zahl an eine [andere] Zahl eine größere Zahl ergibt.“50
2. suppositio:
„Wenn sich gewisse Quantitäten in einem rationalen Verhältnis verhalten, verhalten sie sich wie zwei Zahlen und umgekehrt.“51
3. suppositio:
„Wenn zwei Quantitäten sich in einem rationalen Verhältnis zueinander verhalten, verhält sich ein Aggregatum aus ihnen in Bezug auf eine beliebige jener Quantitäten in einem rationalen Verhältnis.“52
4. suppositio:
„[Das Verhältnis] einer Seite zu dem Überhang, durch den eine Diagonale eine Seite überragt, ist ein irrationales Verhältnis.“53 Alvarus Thomas leitet dies aus der 4. conclusio des dritten Kapitels im ersten Teil des Liber de triplici motu ab.
5. suppositio:
„Wenn das Verhältnis einer größeren Quantität zu irgendeinem irgendwievielten Teil einer irgendwie großen kleineren Quantität rational sei, würde das Verhältnis derselben größeren Quantität zur gesamten kleineren Quantität ein rationales [Verhältnis] sein.“54
6. suppositio:
„Wenn zwei ungleiche Quantitäten sich in einem rationalen Verhältnis verhalten, verhält sich jede bei beiden [Quantitäten] in Bezug auf den Überhang, durch den die größere [Quantität] die kleinere [Quantität] überragt, in einem rationalen Verhältnis oder [in einem Verhältnis] der Gleichheit.“55
Die conclusiones
1. conclusio:
„Es gibt unendliche species eines irrationalen Verhältnisses, die kleiner als ein doppeltes [Verhältnis] sind. Und irgendeines von ihnen ist bis ins Unendliche klein.“56 Alvarus Thomas zeigt dies, indem er den Überhang einer Diagonalen eines Quadrats immer weiter halbiert und feststellt, dass die jeweilige Hälfte ebenfalls irrational ist, und die Summe der jeweiligen Hälfte und der Seite im Verhältnis zur Seite ein irrationales Verhältnis bilden, das kleiner als ein doppeltes Verhältnis wäre. Und da man den Überhang durch beliebig viele Zahlen teilen kann, gibt es unendlich viele irrationale Verhältnisse, die kleiner als ein doppeltes Verhältnis sind.57
Korollar: „Es können auf unendliche Weisen unendliche species eines irrationalen Verhältnisses, die kleiner als ein doppeltes [Verhältnis] sind, erzeugt werden, wie es auch möglich ist, wenn der Überhang der Diagonalen durch verhältnismäßige Teile gemäß einem doppelten Verhältnis vermindert wird, oder auf andere Weise gemäß einem dreifachen Verhältnis oder gemäß einem vierfachen [Verhältnis] oder gemäß einem anderthalbfachen [Verhältnis] und so bis ins Unendliche.“58
2. conclusio:
„Unendliche sind die species eines irrationalen Verhältnisses, das größer als ein doppeltes [Verhältnis] ist. Irgendeins von jenen ist unendlich groß.“59 Beim Beweis stellt Alvarus Thomas fest, dass das Verhältnis einer Quadratseite zum Überhang, durch den die Diagonale die Seite übertrifft, größer als ein doppeltes Verhältnis ist. Durch die stetige Halbierung des Überhangs entstehen neue irrationale Verhältnisse aus der jeweiligen Hälfte und der Seite, die immer größer als ein doppeltes Verhältnis sein werden.60
Kapitel 1.5
Im fünften Kapitel stellt Alvarus Thomas Aussagen über die Teilung eines Körpers nach rationalen Verhältnissen auf. Das Kapitel beginnt mit vier suppositiones. Diese suppositiones führen zu sechs conclusiones. Im Anschluss an den letzten Korollar der conclusiones finden sich Rechenbeispiele für die Aufteilung gemäß doppelt, dreifach und vierfach superpartikularen Verhältnissen.
Die suppositiones
1. suppositio:
„Nicht alle Teile irgendeines Körpers, in die derselbe Körper geteilt wird, verhalten sich stetig in demselben Verhältnis. Ein Beispiel: Alle verhältnismäßigen Teile desselben Körpers sind in demselben Verhältnis A. Das wird bewiesen, weil es möglich ist, dass eine Hälfte irgendeines Körpers in alle seine Teile gemäß einem dreifachen Verhältnis geteilt werden kann. Und alle jene Teile sind Teile jenes Gesamtkörpers, in die derselbe Körper geteilt wird. Und sie verhalten sich stetig in einem dreifachen Verhältnis. Und dennoch sind nicht alle Teile jenes Körpers verhältnismäßig gemäß einem dreifachen Verhältnis.“61
2. suppositio:
„Alle Teile irgendeines gekennzeichneten Körpers verhalten sich stetig gemäß irgendeinem Verhältnis, nämlich A. Sie lösen den ganzen Körper auf. Alle verhältnismäßigen Teile desselben Körpers sind gemäß dem Verhältnis A. Und ich möchte sagen, wenn irgendein Körper stetig in unendliche Teile geteilt wird, die sich in dem Verhältnis A zueinander verhalten und den ganzen Körper auflösen, dass [dann] alle jene Teile zugleich verhältnismäßig gemäß dem Verhältnis A sind.“62
3. suppositio:
„Wann auch immer irgendetwas stetig verhältnismäßig gemäß irgendeinem geometrischen Verhältnis eingerichtet wird, [gilt]: Wie das Verhältnis zwischen den proportionierten [Termen] ist, so ist es zwischen ihren differentiae beziehungsweise den Überhängen – was dasselbe ist – zum Beispiel verhält sich 8 zu 4 in einem doppelten Verhältnis verhält und ebenso 4 zu 2 – sie werden stetig verhältnismäßig eingerichtet gemäß demselben Verhältnis. Daher verhält sich die differentia oder der Überhang zwischen 8 und 4 zur differentia oder zum Übergang zwischen 4 und 2 in einem doppelten Verhältnis.“63
4. suppositio:
„Wenn irgendein Körper in unendliche Teile geteilt wird, verliert er durch das Abziehen des ersten [Teils] von jenen irgendein Verhältnis, zum Beispiel A. Das bedeutet, dass er um das Verhältnis A kleiner wird. Und beim Abziehen des zweiten [Teils] nach dem ersten [Teil] wird er erneut um A kleiner, und beim Abziehen des dritten [Teils] nach dem zweiten [Teil] wird er erneut kleiner um das Verhältnis A. Und so sind folgerichtig jene Teile alle verhältnismäßigen Teile jenes Körpers gemäß dem Verhältnis A. Wenn er aber beim Abziehen des ersten [Teils] von jenen nicht einen Teil gemäß Verhältnis A verliert, und beim Abziehen des zweiten [Teils] nach dem ersten [Teils] einen anderen [Teil verliert], beim Abziehen des dritten [Teils] nach dem zweiten einen anderen gemäß dem Verhältnis A [Teil verliert] und so weiter, sind solche Teile nicht alle verhältnismäßigen Teile eines solchen Körpers gemäß dem Verhältnis A.“64
Die conclusiones
1. conclusio:
„Wenn auch immer irgendein Körper in eine beliebige Klasse eines Verhältnisses geteilt wird, muss sich der ganze Körper zu dem Aggregatum aus allen verhältnismäßigen Teilen, die dem ersten [Teil] folgen, in dem Verhältnis verhalten, durch das der Körper geteilt wurde.“65
2. conclusio, die den residuum a prima parte definiert:
„Um den Rest von ersten verhältnismäßigen Teil einzuführen, wird ein Körper in einem beliebigen rationalen Verhältnis geteilt. Man erfasse die Erstzahlen eines solchen Verhältnisses. Und der Körper wird in so viele Einheiten geteilt, wie die größere Zahl jenes Verhältnisses. Und von jenen Teilen erfasse man so viele als Rest vom ersten Teil, wie es die kleinere Zahl eines solchen Verhältnisses ist.“66
3. conclusio:
„Um einen Körper in verhältnismäßige Teile gemäß einem beliebigen vielfachen Verhältnis zu teilen, muss als Rest vom ersten verhältnismäßigen Teil ein irgendwievielter Teil erfasst werden, der bestimmt wird von der Zahl, die ein solches vielfaches Verhältnis bestimmt. So muss bei einer Teilung gemäß einem doppelten Verhältnis eine Hälfte als Rest vom ersten verhältnismäßigen Teil erfasst werden, und gemäß einem dreifachen Verhältnis ein Drittel und gemäß einem vierfachen [Verhältnis] ein Viertel und bei einem fünffachen [Verhältnis] ein Fünftel und so weiter bis ins Unendliche.“67
1. Korollar: „Beim Teilen eines Körpers gemäß einem doppelten Verhältnis wird der erste Teil die Hälfte sein, und der zweite Teil [wird] die Hälfte des Rests [sein], und der dritte [Teil wird] die Hälfte des Rests [sein] und folgerichtig so weiter. Bei einem dreifachen Verhältnis ist der erste Teil zwei Drittel des ganzen [Körpers], und der zweite [Teil ist] zwei Drittel des Rests, und der dritte [Teil ist] zwei Drittel des Rests vom ersten und zweiten [Teil] und weiter so ohne Ende, bei einem vierfachen [Verhältnis] aber [ist] der erste Teil drei Viertel, und der zweite [Teil ist] drei Viertel des Rests, bei einem fünffachen Verhältnis ist der erste Teil vier Fünftel, und bei einem sechsfachen [Verhältnis ist er] fünf Sechstel, und bei einem siebenfachen [Verhältnis ist er] sechs Siebentel und so weiter ohne Ende.“68
2. Korollar: Bei einer Teilung nach einem n-fachen Verhältnis ist das Verhältnis des Rests des ersten verhältismäßigen Teil zum ersten verhältnismäßigen Teil durch n-1 teilbar. Es heißt: „Beim Teilen eines Körpers durch verhältnismäßige Teile gemäß einem doppelten Verhältnis ist der Rest vom ersten [Teil] gleich dem ersten Teil. Und bei einem dreifachen Verhältnis ist er das durch 2 Geteilte in Beziehung zum ersten [Teil]. Und in einem vierfachen [Verhältnis] [ist er] das durch 3 Geteilte, und in einem fünffachen [Verhältnis] [ist er] das durch 4 Geteilte, und in einem sechsfachen [Verhältnis] [ist er] das durch fünf Geteilte und so weiter ohne Ende.“69
Und weiter: „Denn wenn beim Teilen gemäß einem dreifachen Verhältnis der erste Teil zwei Drittel ist, und der Rest [ist] ein Drittel, und weil ein Drittel in Beziehung zu zwei Dritteln das durch 2 Geteilte sei, [dann] wird der Rest vom ersten Teil durch das Teilen gemäß eines dreifachen Verhältnisses in Beziehung zum ersten [Teil] durch 2 geteilt sein. Ebenso, wenn beim Teilen eines Körpers gemäß einem vierfachen Verhältnis der erste Teil drei Viertel ist und der Rest vom ersten [Teil] ein Viertel. Ein Viertel aber ist das durch 3 Geteilte in Bezug zu drei Vierteln. Daher ist der Rest von ersten Teil beim Teilen gemäß einem vierfachen [Verhältnis] in Bezug auf den ersten Teil durch 3 geteilt. Und auf diese Art und Weise wird man die anderen beweisen.“70
4. conclusio:
„Um einen Körper nach einem beliebigen superpartikularen Verhältnis zu teilen, muss für den ersten verhältnismäßigen Teil ein irgendwievielter Teil erfasst werden, der von der größeren Zahl der Erstzahlen eines solchen Verhältnisses bestimmt wird.“71
Korollar: „Bei der Teilung eines Körpers durch verhältnismäßige Teile gemäß einem anderthalbfachen Verhältnisses ist der Rest vom ersten Teil Zwei in Bezug auf die erste [Zahl] und bei einem Vierdrittel[verhältnis] Drei und bei einem Fünfviertel[verhältnis] Vier und bei einem Sechsfünftel[verhältnis] Fünf und so bis ins Unendliche. Auf umgekehrte Art und Weise ist es bei den species eines vielfachen Verhältnisses, indem von der Drei begonnen werden muss.“72
5. conclusio:
„Um einen Körper gemäß dem suprapartienten Verhältnis, welches einem gefällt, zu teilen, werden species dieses Verhältnisses in einer Reihe erzeugt in der Art und Weise, wie es im zweiten Kapitel dieses Teils dargelegt wurde. Und der Körper werde in so viele Teile geteilt, wie es die Anzahl der unteren Ordnung ist. Und aus jenen Teilen erfasse man so viele für den Rest vom ersten verhältnismäßigen Teil, wie es die obere Zahl ist. Und der Rest wird der erste verhältnismäßige Teil sein.“73
exemplum: „Ein Beispiel: Eine natürliche Reihe an Zahlen, wobei von der Drei angefangen werden muss, werde aufgestellt, und eine Reihe aller ungeraden Zahlen werde darunter aufgestellt, wobei mit der Fünf angefangen werden muss, wie es aus dem Bild ersichtlich ist.“74

Abb. 10: Alvarus Thomas, Liber de triplici motu, S. 11.
Und weiter: „Wenn man dann irgendeinen Körper gemäß einem Fünfdrittelverhältnis teilen will, weil die unterere Zahl in jener species 5 ist, teile man den ganzen Körper in fünf Fünftel. Und weil die oberere Zahl Drei ist, erfasse man für den Rest vom ersten verhältnismäßigen Teil drei Fünftel, und es werden zwei Fünftel bleiben. Und jene zwei Fünftel sind der erste verhältnismäßige Teil gemäß einem Fünfdrittelverhältnis. Und auf diese Art und Weise wird man bei allen anderen species verfahren. Und wie im zweiten Kapitel, wo die species dieses Verhältnisses erzeugt werden, nicht alle [species] erzeugt werden, obwohl unendliche [species] erzeugt werden, solle man die Lehre der zweiten conclusio nutzen, um einen Körper gemäß einem suprapartienten Verhältnis, das man wolle, zu teilen.“75
1. Korollar: „Bei der Teilung eines Körpers nach der ersten species eines weiter unten ausgezeichneten suprapartienten Verhältnisses ist der Rest vom ersten verhältnismäßigen Teil anderthalbfach in Bezug zum ersten [Teil]. Und bei der zweiten species ist der Rest vom ersten [Teil] vierdrittelfach in Bezug auf den ersten [Teil]. Und in der dritten species ist er fünf Viertel zum ersten [Teil]. Und in der vierten [species] wird der Rest vom ersten [Teil] sechs Fünftel [zum ersten Teil] sein und so bis ins Unendliche beim Voranschreiten durch die species eines superpartikularen Verhältnisses.“76
6. conclusio:
„Um einen Körper gemäß einem beliebigen vielfachen superpartikularen Verhältnis zu teilen, sollen species dieses Verhältnisses in Zahlen nach der Art, wie sie im zweiten Kapitel dieses Teils dargelegt werden, erzeugt werden. Und man solle den Körper in so viele Teile teilen, wie es die Zahl der untereren Reihe ist. Und aus jenen Teilen solle man so viele für den Rest vom ersten verhältnismäßigen Teil erfassen, wie es die oberere Zahl ist. Und der Rest wird der erste verhältnismäßige Teil sein. Und auf dieselbe Art und Weise geschehe es, sobald ein vielfach suprapartientes Verhältnis geteilt werden muss, wie um einen Körper gemäß einem fünfhalbefachen Verhältnis zu teilen. Weil die größere Zahl in jener species Fünf ist, solle man den Körper in fünf Fünftel teilen. Und weil die kleinere Zahl Zwei ist, fasse man zwei Fünftel für den Rest vom ersten verhältnismäßigen Teil, und drei Fünftel werden der erste verhältnismäßige Teil sein. Und drei Fünftel des Rests im zweiten [Teil] und ebenso drei Fünftel des Rests vom ersten [Teil] und zweiten [Teil] und dritten [Teil] und weiter so ohne Ende. Ebenso wenn man einen Körper gemäß einem Achtdrittelverhältnis teilen will, teile man den Körper in acht Achtel, weil die Zahl Acht die größere Zahl jenes Verhältnisses ist. Und man fasse für den Rest vom ersten verhältnismäßigen Teil drei Achtel. Und die restlichen fünf Achtel werden der erste verhältnismäßige Teil sein. Und fünf Achtel des Rests werden der zweite verhältnismäßige Teil sein und folgerichtig so weiter.“77
1. Korollar: „Daraus folgt, dass bei allen species eines vielfachen superpartikularen Verhältnisses oder eines vielfach suprapartienten [Verhältnisses] und sogar bei allen anderen [Verhältnissen] der Rest vom ersten verhältnismäßigen Teil sich zum ersten verhältnismäßigen Teil in dem Verhältnis verhält, in dem sich die oberen Zahlen in den Bildern ihrer Erzeugung zu den Zahlen verhalten, durch die die unteren [Zahlen] die oberen [Zahlen] übertreffen, wie in einen fünfhalbefachen Verhältnis, weil die obere Zahl Zwei ist und die untere Zahl Fünf, und Fünf die Zwei um Drei übertrifft, verhält sich der Rest vom ersten verhältnismäßigen Teil in einem solchen Verhältnis zum ersten verhältnismäßigen Teil wie Zwei zu Drei. In einem Achtdrittelverhältnis ist die obere Zahl die Drei und die untere Acht. Und die Acht übertrifft die Drei um Fünf. Daher verhält sich bei der Teilung eines solchen Verhältnisses der Rest vom ersten verhältnismäßigen Teil zum ersten [Teil] wie Fünf zu Drei.“78
Weitere exempla
Einleitung: Es heißt, „um auch ein Übungsverfahren dieses [letzten] Korollars zu erhalten, stelle man einige Bilder nach dem Erzeugen von Verhältnissen auf, durch die leicht entschieden werden wird, in welchem Verhältnis sich der Rest vom ersten verhältnismäßigen Teil zum ersten verhältnismäßigen Teil verhält.“79
1. exemplum: „Um einen leichten Einblick in doppelt superpartikulare Verhältnisse zu erlangen, stelle man eine natürliche Reihe an Zahlen auf, wobei mit der Zwei in der untereren Linie begonnen werden muss. Und in der oberen Linie stelle man eine natürliche Ordnung an Zahlen auf, wobei mit der Drei begonnen. Und indem ein Bezug von der ersten [Zahl] der unteren Ordnung zur ersten [Zahl] der oberen [Ordnung] hergestellt werden muss, wird man ein solches Verhältnis erhalten, in dem sich der Rest vom ersten verhältnismäßigen Teil zum ersten [Teil] beim Teilen eines Körpers gemäß der ersten species eines doppelt superpartikularen Verhältnisses verhält. Und indem die zweite [Zahl] der unteren Klasse auf die zweite [Zahl] der oberen [Ordnung] bezogen werden muss, wird man dasselbe bei der zweiten species eines doppelt superpartikularen Verhältnisses erhalten. Und derart folgerichtig weiter, wie es in dem Bild offensichtlich ist.“80

Abb. 11: Alvarus Thomas, Liber de triplici motu, S. 12.
2. exemplum: „Aber zur Übung dieser Beschäftigung bei species eines dreifachen superpartikularen Verhältnisses solle man in der unteren Reihe eine natürliche Ordnung an Zahlen aufstellen, wobei mit der Zwei begonnen werden muss. Und in der oberen [Ordnung] stelle man alle ungeraden Zahlen auf, wobei mit der Fünf begonnen werden muss, wobei die erste [Zahl] der unteren Ordnung auf die erste [Zahl] der oberen [Ordnung], und die zweite [Zahl] der unteren [Ordnung] auf die zweite [Zahl] der oberen [Ordnung], und die dritte [Zahl] der unteren [Ordnung] auf die dritte [Zahl] der oberen [Ordnung] und folgerichtig so weiter bezogen werden muss. In dem Verhältnis, das man erblicken wird, verhält sich der Rest vom ersten verhältnismäßigen Teil zum ersten [Teil] nach dem Vollzug der Teilung des Körpers gemäß einem dreifachen suprapartienten Verhältnis, wie es in dem Bild offensichtlich ist.“81

Abb. 12: Alvarus Thomas, Liber de triplici motu, S. 12.
3. exemplum: „Um auch so bei den species eines vierfach superpartikularen [Verhältnisses], eines fünffach superpartikularen [Verhältnisses] und so weiter zu üben, solle man eine natürliche Reihe an Zahlen aufstellen, wobei mit der Zwei in der unteren Linie begonnen werden muss. Und in die obere [Ordnung stelle man] alle Zahlen, die sich stetig um Drei überschreiten, wobei mit der Sieben angefangen werden muss. Und so wird man das erhalten, sobald man nach den species eines vierfach superpartikularen Verhältnisses sucht. Um das in die species eines fünffach superpartikularen Verhältnisses einzuführen, stelle man in der oberen Klasse alle Zahlen, die sich um 4 übertreffen, wobei mit der Zahl Neun angefangen werden muss. Und für die folgende species stelle man in die obere Klasse alle Zahlen, die sich um Fünf überschreiten, wobei mit der Elf angefangen werden muss. Und derart folgerichtig wird man in den anderen species verfahren. Das ist offensichtlich in den folgenden Bildern.“82

Abb. 13: Alvarus Thomas, Liber de triplici motu, S. 12.
4. exemplum: „Aber zur Übung dieses letzten Korollars in den species vielfach superpartikularer [Verhältnisse] werden auch einige Beispiele aufgestellt, um es zu verdeutlichen. Um daher leicht ein Verhältnis des Rests vom ersten verhältnismäßigen Teil zu demselben ersten [Teil] in den species eines doppelt suprapartienten Verhältnisses einzuführen, solle man eine natürliche Reihe aufstellen, wobei von der Drei in der unteren Linie angefangen werden muss. In der oberen [Ordnung] aber solle man alle ungleichen Zahlen aufstellen, wobei mit der Fünf angefangen werden muss, und wobei dann die erste [Zahl] der unteren Ordnung mit der ersten [Zahl] der oberen [Ordnung], und die zweite [Zahl] mit der zweiten [Zahl], und die dritte [Zahl] mit der dritten [Zahl] in Beziehung gestellt werden muss. Das, was man sucht, wird man leicht finden, wie es offensichtlich ist in der folgenden Figur.“83

Abb. 14: Alvarus Thomas, Liber de triplici motu, S. 12.
5. exemplum: „Um auch das Verhältnis des Rests vom ersten verhältnismäßigen Teil zu demselben ersten [Teil] einzuführen, wenn man eine Teilung eines Körpers gemäß einem dreifach suprapartienten Verhältnis macht, solle man über eine natürliche Reihe an Zahlen, wobei mit der Drei angefangen werden muss, eine Reihe aller Zahlen stellen, die sich stetig um Drei übertreffen, wobei mit der Nummer Acht angefangen werden muss. So ist es offensichtlich in dem Bild.“84

Abb. 15: Alvarus Thomas, Liber de triplici motu, S. 12.
6. exemplum: „Um auch den Vorschlag für die species eines vierfach suprapartienten Verhältnisses einzuführen, solle man über eine natürliche Reihe an Zahlen, wobei mit der Drei angefangen werden muss, eine Reihe an Zahlen stellen, die sich stetig um Vier übertreffen, wobei mit der Elf angefangen werden muss. Und [für die species eines vierfach suprapartienten Verhältnisses und] so weiter solle man über dieselbe natürliche Reihe an Zahlen, wobei mit der Drei angefangen werden muss, eine Reihe an Zahlen stellen, die sich stetig um Fünf übertreffen, wobei mit der Vierzehn angefangen werden muss. Und derart wird man folgerichtig bei den anderen verfahren. Und so viel zur Teilung der Körper nach einem rationalen Verhältnis.“85
Kapitel 1.6
Das sechste Kapitel beschäftigt sich mit der Teilung eines Körpers nach irrationalen Verhältnissen. Alvarus Thomas stellt diesmal keine neuen suppositiones auf. Es heißt: „Wie ein beliebiger Körper nach einem rationalen Verhältnis und seinen unendlichen species geteilt werden kann, wie es das vorhergehende Kapitel zeigt, so kann auch ein beliebiger Körper gemäß einem irrationalen Verhältnis und seinen unendlichen species geteilt werden.“86 Es gelten also die suppositiones des letzten Kapitels, zu denen weitere drei conclusiones hinzugefügt werden.
1. conclusio:
„Ein beliebiger Körper, der nach irgendeinem irrationalen Verhältnis geteilt wurde, muss sich zu dem Aggregatum aus allen verhältnismäßigen Teilen gemäß eines solchen Verhältnisses, die dem ersten [Teilen] folgen, in dem Verhältnis verhalten, durch das der ganze [Körper] geteilt wird.“87
2. conclusio:
In der zweiten conclusio differenziert er wie im vierten Kapitel des ersten Teils zuerst zwischen irrationalen Verhältnissen, die größer beziehungsweise kleiner als ein doppeltes Verhältnis sind, beschreibt dann aber nur diejenigen, die kleiner als ein doppeltes Verhältnis sind. Es heißt: „Um einen Körper gemäß unendlichen irrationalen Verhältnissen zu teilen, die kleiner als ein doppeltes [Verhältnis] sind, wie zum Beispiel gemäß dem Verhältnis einer Diagonalen zur Seite, oder dem [Verhältnis] eines Aggregatums aus der Hälfte des Überhangs, durch den eine Diagonale die Seite übertrifft, und der Seite selbst zu derselben Seite und folgerichtig so weiter, wie es im vierten Kapitel dargestellt wurde, muss der Überhang, durch den eine größere Quantität die kleinere [Quantität] übertrifft, für den ersten Teil erfasst werden. Daher wird der Rest vom ersten [Teil] die kleinere Quantität sein. Und der ganze Körper sei die größere Quantität eines solchen Verhältnisses.“88
1. Korollar: „Um einen Körper gemäß dem irrationalen Verhältnis einer Diagonalen zur Seite [eines Quadrats] zu teilen, ist es notwendig, für den ersten verhältnismäßigen Teil den Überhang zu erfassen, durch den die Diagonale die Seite übertrifft. Und für den zweiten [Teil ist es notwendig,] dann den Überhang erfassen, durch den jene Seite, wenn es die Diagonale des Quadrats ist, die Seite jenes Quadrats übertrifft, und folgerichtig so weiter. Und um den ersten verhältnismäßigen Teil eines irrationalen Verhältnisses zu ergeben, das das Aggregatum aus der Seite und der Hälfte des Überhangs der Diagonalen in Bezug auf dieselbe Seite ist, erfasse man für den ersten verhältnismäßigen Teil jene Hälfte des Überhangs. Und für den zweiten verhältnismäßigen Teil soll man einen so großen Teil des Rests erfassen, zu dem der erste [Teil] jenes Verhältnis hat, das der ganze Körper in Bezug auf das Aggregatum aus allen [Teilen] hat, die dem ersten [Teil] folgen. Und erneut aus dem Rest vom ersten Teil und vom zweiten [Teil] erfasse man für den dritten Teil einen so großen Teil, zu dem der zweite [Teil] jenes Verhältnis hat, das der erste [Teil] zu sich selbst hat, und folgerichtig so weiter. Und auf ähnliche Art und Weise sollte verfahren werden, wenn ein Körper gemäß einem irrationalen Verhältnis geteilt wird, das aus dem Aggregatum der Seite und dem vierten Teil oder dem achten [Teil] oder dem sechzehnten [Teil] des Überhangs, durch den eine Diagonale die Seite übertrifft, zu derselben Seite besteht.“89
2. Korollar: „Nach der Teilung eines Körpers durch verhältnismäßige Teile gemäß einem irrationalen Verhältnis, das aus der Diagonalen zur Seite besteht, verhalten sich alle ungeraden Teile stetig in einem doppelten Verhältnis, und alle geraden [Teile verhalten sich] ebenso, und alle zwei, zwischen denen zwei [Teile] dazwischen liegen, verhalten sich stetig in einem anderthalbfachen Verhältnis zu dem doppelten [Verhältnis]. Und alle, zwischen denen drei [Teile] dazwischen liegen, verhalten sich in einem vierfachen Verhältnis und folgerichtig so weiter.“90 Und weiter heißt es: „Das Korollar ist zur Wahrnehmung in dem folgenden Bild offensichtlich, in dem der erste Teil die Diagonale des größeren dort abgebildeten Quadrats ist. Und der zweite [Teil] ist die Seite desselben Quadrats. Und der dritte [Teil] ist die Seite des folgenden Quadrats. Und der dritte [Teil] ist die Seite des dritten Quadrats und die Diagonale des vierten [Quadrats]. Und der vierte [Teil] ist die Seite des vierten Quadrats und der Diagonale des fünften [Quadrats]. Und der fünfte [Teil] ist die Seite desselben fünften Quadrats. Und so wird man bis ins Unendliche fortschreiten können. Denn dort wird man erblicken, dass [das Verhältnis] des ersten [Teils] zum dritten [Teil] ein doppeltes Verhältnis ist und das [Verhältnis] des zweiten [Teils] zum vierten [Teil] auch ein doppeltes [Verhältnis] ist. Und das [Verhältnis] des ersten [Teils] zum fünften [Teil ist] ein vierfaches [Verhältnis].“91
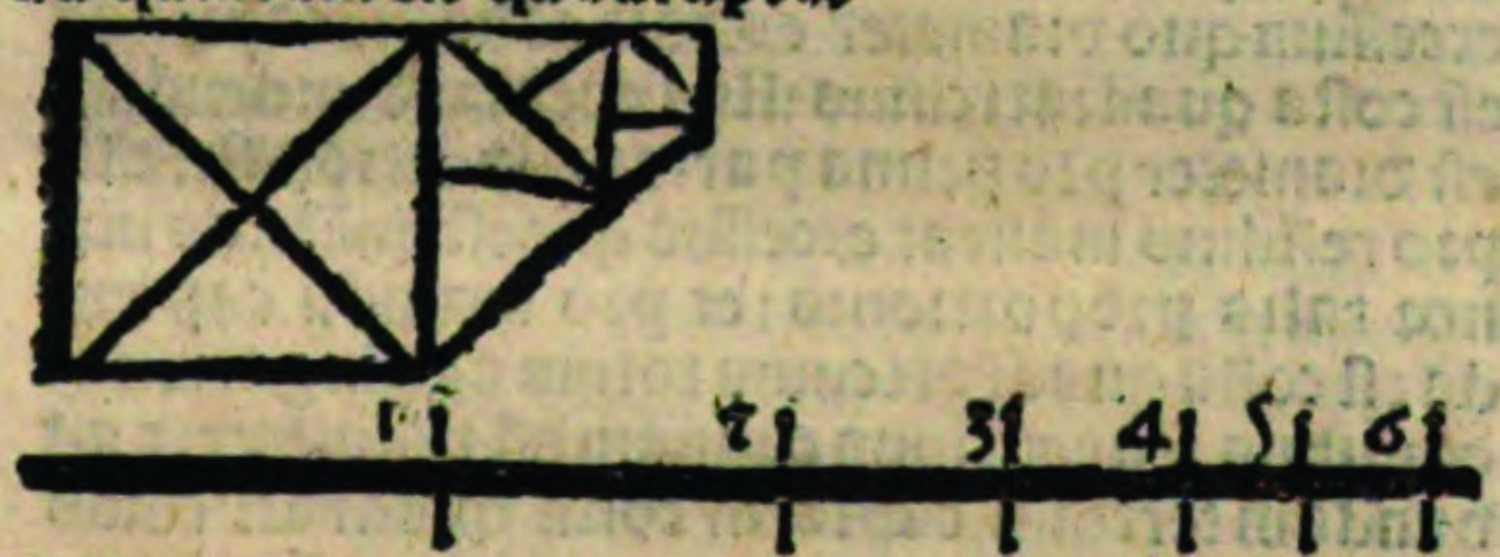
Abb. 16: Alvarus Thomas, Liber de triplici motu, S. 13.
3. Korollar: „Daraus folgt drittens, dass bei einer solchen Teilung das Aggregatum aus allen ungeraden [Teilen] außer dem ersten ungeraden [verhältnismäßigen Teil] gleich dem ersten [verhältnismäßigen Teil] ist; und das Aggregatum aus allen geraden [Teilen] außer dem zweiten [Teil], welcher der erste gerade [Teil] ist, dem zweiten [verhältnismäßigen Teil] gleich ist. Und das Aggregatum aus allen ungeraden [Teilen] verhält sich zu dem Aggregatum aus allen geraden [Teilen] in dem Verhältnis, das das Mittel eines doppelten [Verhältnisses] ist.“92
4. Korollar: „Nach der Teilung eines Körpers in verhältnismäßige Teile gemäß einem irrationalen Verhältnis, welches das Mittel eines dreifachen [Verhältnisses] ist, verhalten sich alle ungeraden Teile einer solchen Teilung in einem dreifachen Verhältnis, und auch alle geraden [Teile]; und alle, zwischen denen drei [Teile liegen], [verhalten sich] in einem neunfaches Verhältnis. Und das Aggregatum aus allen ungeraden [Teilen] verhält sich zu dem Aggregatum aus allen geraden [Teilen] in dem Verhältnis, das das Mittel des dreifachen [Verhältnisses] ist.“93
3. conclusio:
„Um einen Körper in verhältnismäßige Teile nach unendlichen species eines irrationalen Verhältnisses zu teilen, das größer als ein doppeltes [Verhältnis] ist, wie zum Beispiel gemäß dem Verhältnis, das [das Verhältnis] der ganzen Diagonalen zum Überhang ist, durch den dieselbe Diagonale die Seite übertrifft, und [das Verhältnis] der ganzen Diagonalen mit der Hälfte des Überhangs, durch den sie die Seite übertrifft, zu einem Viertel oder zu einem Fünftel oder zu einem Sechstel, wie weiter oben besprochen worden ist, muss als erster verhältnismäßiger Teil der Überhang erfasst werden, durch den die größere Quantität die kleinere [Quantität] in einem solchen Verhältnis übertrifft, und die kleinere Quantität für den Rest. Wie wenn man will, dass der Körper in verhältnismäßige Teile gemäß dem Verhältnis geteilt wird, das [das Verhältnis] der ganzen Diagonalen zum Überhang ist, durch den die Diagonale die Seite übertrifft, [dann] muss die Seite des Quadrats erfasst werden, durch der Körper geteilt werden muss, [und] die Diagonale für den ersten verhältnismäßigen Teil. Und so bliebe für die restlichen [Teile] der Überhang, der die kleinere Quantität eines solchen Verhältnisses ist. Und für den zweiten [Teil] muss die Seite des Quadrats erfasst werden, dessen Diagonale das gesamte Aggregatum aus allen [Teilen] ist, die dem ersten [Teil] folgen. Und um den dritten [Teil] zu ergeben, soll man die Seite des Quadrats erfassen, dessen Diagonale das Aggregatum aus allen [Teilen] ist, die dem ersten [Teil] und dem zweiten [Teil] folgen. Und um irgendeinen Körper gemäß dem Verhältnis zu teilen, das das [Verhältnis] der ganzen Diagonalen zu Hälfte des Überhangs ist, durch den er die Seite übertrifft, muss für den ersten verhältnismäßigen Teil der Überhang erfasst werden, durch den die größere Quantität die kleinere [Quantität] in einem solchen Verhältnis übertrifft. Denn der ganze Körper muss durch die Diagonale irgendeines Quadrats aufgestellt werden. Und dann muss für den ersten verhältnismäßigen Teil ein so großer Teil des Körpers erfasst werden, dass für alle folgenden [Teile] keiner außer der Hälfte des Überhangs bliebe, durch – wenn ein solcher Körper da ist – die Diagonale die Seite desselben Quadrats übertrifft. Und um den zweiten verhältnismäßigen Teil zu ergeben, soll man den ganzen [Rest] aufstellen, der dem ersten [Teil] als Diagonale irgendeines Quadrats folgt. Und für den zweiten Teil soll man soviel erfassen, dass für die folgenden [Teile] nichts außer der Hälfte des Überhangs bliebe, durch den eine solche Diagonale seine Seite übertrifft, und folgerichtig so weiter.“94 Alvarus Thomas verweist auf die Korollare der zweiten conclusio dieses Kapitels, wenn man weitere Eigenschaften errechnen will.95
Kapitel 1.7
Im siebenten Kapitel setzt sich Alvarus Thomas mit Verhältnissen der ordines von verhältnismäßigen Teilen auseinander, die bei der Teilung eines Körpers nach einem gewissen Verhältnis entstehen wie z.B. die ordines der ungeraden und geraden Teile. Er bezeichnet solche Verhältnisse als interskalar und deutet an, dass diese später für Berechnung von Bewegungen wichtig werden.96 Drei conclusiones werden dargestellt:
1. conclusio:
Die ordines der verhältnismäßigen Teile befinden sich in dem Verhältnis der Teilung des Körpers zueinander. Es heißt: „Nach der Teilung eines Körpers in verhältnismäßige Teile gemäß einem beliebigen Verhältnis und nach dem Erfassen fest stehender Ordnungen von verhältnismäßigen Teilen, die sich dazwischen interskalar verhalten und die den ganzen Körper auflösen, verhalten sich jene Ordnungen stetig in dem Verhältnis der Teilung. Wenn zum Beispiel ein Körper gemäß einem doppelten Verhältnis geteilt wird, und alle Teile erfasst werden, zwischen denen sich zwei [Teile befinden], für die erste Ordnung nämlich der erste [Teil], der vierte, der siebente, der zehnte, der dreizehnte und so weiter und danach für die zweite Ordnung der zweite, der fünfte, der achte, der elfte und der vierzehnte [Teil] und folgerichtig so weiter und eben auch für die dritte Ordnung der dritte, der sechste, der neunte, der zwölfte und der fünfzehnte [Teil] der Reihe nach erfasst werden – sage ich, dass die erste Ordnung sich zur zweiten [Ordnung] in einem doppelten Verhältnis verhält, und sich auch die zweite [Ordnung] zur dritten [Ordnung] in einem doppelten Verhältnis [befindet].“97
Und weiter heißt es: „Wann auch immer irgendwelche [Subjekte] gemäß einem gleichen Verhältnis geteilt wird, gilt: In welchem Verhältnis auch immer sich die ersten verhältnismäßigen Teile zueinander verhalten, in demselben Verhältnis verhalten sich die ganzen [Subjekte] selbst, weil sie ja irgendwievielte Teile derselben denominatio sind. In welchem Verhältnis auch immer sich dann die irgendwievielten Teile derselben denominatio verhalten, in demselben [Verhältnis] verhalten sich selbst die ganzen [Subjekte], dessen irgendwievielte Teile es sind, wie später nachgewiesen wird. Daher.“98
2. conclusio:
Alvarus Thomas zeigt ein Verfahren, wie man die Anzahl der verhältnismäßigen Teile einer jeweiligen festgelegten Ordnung bei der Teilung eines Körpers nach einem bestimmten Verhältnis berechnen kann. Es heißt: „Um zu wissen, der wievielte irgendwievielte Teil oder die wievielten irgendwievielte Teile eine beliebige jener Ordnungen ist, muss angesehen werden, wie viele Ordnungen es gibt. Und dann solle man aus den Zahlen so viele Verhältnisse einer Teilung aufstellen, wie es sie von einer Ordnung gibt, nachdem eine weggenommen wurde. Und alle Terme jener Verhältnisse sollen sich vereinigen. Und das ganze [Subjekt] soll man in so viele irgendwievielte Teile teilen wie die Anzahl, die daraus entspringt. Und es sollen sich bei der ersten Ordnung so viele aus jenen Teilen ergeben, wie die größte Zahl in jenen Verhältnissen ist, und bei der zweiten Ordnung so viele, wie es die zweit[höchste] Zahl ist, und folgerichtig so weiter. Und so wird man sehen, wie viele irgendwievielte Teile es gibt, und wessen denominatio die erste Ordnung innehält und auch die zweite [Ordnung], die dritte [Ordnung] und folgerichtig so weiter.“99
3. conclusio:
Man kann aus der Angabe eines Teils und dem Verhältnis einer ordo wiederum auf das Verhältnis der Teilung eines Körpers schließen. Es heißt: „Es gibt die Teile irgendeines stetigen [Körpers]. Ein irgendwievielten [Teil] erwirbt irgendein rationales Verhältnis. [Es gilt], das erworbene Verhältnis des ganzen [Körpers] zu finden, wie wenn man einen Körpers in fünf irgendwievielte Teile einteile, zum Beispiel in 5 Fünftel, und eines jener [Fünftel] ein doppeltes Verhältnis erwirbt, um das Verhältnis zu finden, welches jener ganze Körper erwirbt. Denn in jenem Fall erwirbt jener Körper ein Sechsfünftelverhältnis, weil er zu sich ein Fünftel erwirbt. Das ist so viel, wie eines seiner Fünftel.“100
Und weiter: „Wenn er nun ein rationales, [aber] nicht vielfaches [Verhältnis] erwirbt, ist festgelegt, dass jenes von irgendeinem irgendwievielten Teil oder von irgendwelchen irgendwievielten Teilen genau oder ungenau – das ist aber nicht die Sorge – bestimmt wird, wie das Siebendrittel[verhältnis] von der Zahl Zwei mit einem Drittel bestimmt wird, und ein Fünfdrittel[verhältnis] von der Eins mit zwei Dritteln.“101
Und weiter: „Wenn aber eines jener Siebentel ein Siebendrittel[verhältnis] erwirbt, teile man ein beliebiges Siebentel in Drittel. Und vervielfache die Sieben mit Drei. Und man wird – wie gesagt worden ist – Einundzwanzig erhalten. Und weil ein Siebentel so viel erwirbt, wie es selbst ist, zum Beispiel ein Siebentel des ganzen [Subjekts] mit einem Drittel jenes Siebentel, teile man auch jenes erworbene Siebentel in drei Teile. Und jene drei Teile werden drei Einundzwanzigstel des ganzen [Subjekts] sein, wie es fest steht. Und das ganze [Subjekt] hat jene drei [Teile] erworben und dazu einen.“102
Und zuletzt: „Und auf diese Art und Weise wird man in jeder anderen species eines Verhältnisses verfahren. Und daraus wird man das Verhältnis finden können, das das ganze [Subjekt] erwirbt, wenn zwei irgendwievielte ungleiche Teilen von ihm oder zwei, die nicht einen [Teil] ausmachen, oder mehrere Teile ein gleiches oder ungleiches Verhältnis erwerben. Und ähnlicherweise wird man erkennen, welches Verhältnis das ganze [Subjekt] verliert, wenn irgendein Teil von ihm oder irgendwelche irgendwievielten Teile ein oder einige Verhältnisse verlieren.“103
Kapitel 1.8
Das achte Kapitel beinhaltet Aussagen über das Verhältnis der Ungleichheit mit Bezug auf zusammengesetzte Zahlen. Diesen Schritt erachtet er als notwendig, wenn man die Verhältnislehre für die Berechnung von Bewegungen verstehen will. Er führt fort, dass man in dieser Situation mit Brüchen statt mit ganzen Zahlen rechnen muss.104 Das Kapitel beginnt mit der Aufstellung von vier suppositiones. Daraus leitet Alvarus Thomas im achten Kapitel des ersten Teils keine conclusiones ab, sondern stellt zwei Regeln auf. Unter Regeln versteht Alvarus Thomas an dieser Stelle Rechenverfahren, die ich der Kürze wegen formal ausdrücken werde.
Die suppositiones
1. suppositio:
„Ich nehme als erstes an, dass eine Zahl etwas Zweifaches ist, wie es sich bei dem Vorschlag darbietet. Diese ist [einerseits] sozusagen aus teilbaren Einsen zusammengesetzt, von denen eine beliebige Eins eine teilbare Sache ist, wie die Anzahl drei Füße, vier Quantitäten und so weiter. Andererseits ist die Zahl ist aus unteilbaren Einsen zusammengesetzt, wie die Anzahl von 5 Punkten, 5 intelligentiae und 10 rationale Seelen.“105
2. suppositio:
In der zweiten suppositio legt er dar, dass, wenn Mengen aus unteilbaren Sachen bestehen, sie nicht durch jede beliebige Zahl teilbar sind. Es heißt: „Nicht jede Zahl ist durch 2 teilbar. Und nicht jede ist durch 3 teilbar und folgerichtig so weiter. Das wird bewiesen, weil ja irgendeine Zahl, nämlich eine der unteilbaren Sachen, solcherart sein kann: Die Anzahl dreier Engel kann nicht in zwei Gleiche geteilt werden – daher ist sie nicht durch 2 teilbar und auch nicht in vier gleiche Teile. So ist sie nicht durch 4 teilbar. Bei anderen wird das [auch] so bewiesen. Daher ist die suppositio wahr.“106
3. suppositio:
„Jede Anzahl von teilbaren Sachen ist durch 2 teilbar oder durch 3 teilbar. Und allgemein kann sie jedes Verhältnis kleinerer oder auch größerer Ungleichheit haben. Der Beweis dieser suppositio: Eine solche Zahl kann in zwei gleiche [Zahlen] geteilt werden, wenn es eine Anzahl an teilbaren Sachen ist, und in drei gleiche [Zahlen] und in 4 und in 5 und so weiter bis ins Unendliche. Darum wird es eine beliebige Zahl geben werden, die ein Verhältnis kleinerer [Ungleichheit] und auch größerer [Ungleichheit] zu [der anderen] selbst hat. Denn zu ihrer Hälfte wird sie ein doppeltes Verhältnis haben und zu ihrem Drittel ein dreifaches [Verhältnis] und zu zwei Dritteln ein anderthalbfaches [Verhältnis] und so weiter bis ins Unendliche.“107
4. suppositio:
„Um irgendeine Zahl durch eine andere [Zahl] zu teilen, die entweder größer oder kleiner oder gleich ist, und die es entweder nötig macht, einen Bruch zu nutzen oder keinen [Bruch], muss eine beliebige Einheit der zu teilenden Zahl in so viele irgendwievielte Teile geteilt werden, wie die Anzahl, durch die diese Teilung geschieht. Und so viele Teile jener müssen zu einer beliebigen Einheit der Zahl gegeben werden, durch die die Teilung geschieht, wie die zu teilende Zahl ist. Und so wird sich eine beliebige Eins gleich verhalten.“108
Die regulae
1. regula:
Die erste Regel betrifft das Teilen einer Zahl nach einem Verhältnis, wie zum Beispiel das Aufteilen der Zahl A nach dem Verhältnis B / C. Die Formel ist A : (B : C ) = (A : B) x C. Es heißt: „Um eine Zahl zu teilen, die sich in dem Verhältnis kleinerer Ungleichheit, in dem man es will, in Bezug auf irgendeine Zahl verhält, die man will, erfasse man aus den Zahlen zwei Zahlen, die sich in einem solchen Verhältnis befinden. Und teile die Zahl in Bezug auf das, dessen Zahl man sucht und die sich in einem Verhältnis kleinerer Ungleichheit befindet, in so viele gleiche Teile, wie es die größere Zahl eines solchen Verhältnisses ist. Und von jenen erfasse man so viele jener Teile, wie es die kleinere Zahl des genannten Verhältnisses ist.“109
2. regula:
Die zweite Regel dagegen lautet A x (B : C) = (A + (B-C)) x (A : C) und erklärt das Multiplizieren einer Zahl mit einem Verhältnis. Es heißt: „Um eine Zahl zu finden, die sich in einem Verhältnis von größerer Ungleichheit zu einer Zahl, die man will, befindet, in welchem Verhältis auch immer es beliebt, [dafür] erfasse man aus den Zahlen zwei Zahlen, die sich in einem solchen Verhältnis befinden. Und man teile die Zahl mit Bezug auf das, dessen Zahl man sucht, und die sich in jenem Verhältnis größerer Ungleichheit befindet, in so viele gleiche Teile auf, wie die kleinere Zahl eines solchen Verhältnisses. Und nachdem jene [Zahl] durch die kleinere Zahl so geteilt wurde, füge man so viele gleiche Teile den Teilen der Teilung zu, wie es die sind, durch die die größere Zahl eines solchen Verhältnisses die kleinere [Zahl] übertrifft. Und dann ist die Zahl, die sich aus der kleineren Zahl und jener Addition ergibt, die Zahl, die sich zu der so geteilten Zahl in dem gegebenen Verhältnis größerer Ungleichheit verhält.“110
Fußnoten
Omnis numerus et similiter omnis qu[an]titas ad alium numerum relatus (ut ait Nicomachus et Boethius in primo arithmeticae) aut est ei aequalis aut inaequalis. Si est aequalis, constituit proportionem aequalitatis, si vero inaequalis, ex eo cum altero inaequalitatis proportio consurgit. Unde proportio est duorum numerorum vel duarum quantitatum unius ad alteram certa habitudo ut habitudo, quae est inter quatuor et 4, et [ea], quae est inter duo et quatuor, et [ea], quae est inter bipedale et pedale. Proportio enim est terminus collectivus pro duabus rebus et signanter quantis vel pro pluribus supponens connotando ipsas esse aequales vel unam alteram aliquo excessu excedere. Thomas 1509, S. 3. Der Zahlenbereich bei Alvarus Thomas ist stets der Bereich der natürlichen Zahlen.
Unde ista consequentia nihil valet: haec proportio est una proportio, ergo est unum ens, quia demonstrato pedali et bipedali non constituentibus unum de illis est verum dicere, quod sunt aliqua proportio, puta dupla, et tamen illa duo non sunt unum ens. Thomas 1509, S. 3.
Duplex autem est proportio, quia quaedam est proportio aequalitatis, alia vero inaequalitatis. Thomas 1509, S. 3.
Proportio aequalitatis est habitudo duarum quantitatum vel numerorum aequalium ut habitudo, quae est inter 8 et 8, pedale et pedale. Et sumatur hic quantitas tam pro quantitate molis quam pro quantitate virtutis, ut capit beatus Augustinus quinto de trinitate. Thomas 1509, S. 3.
Sed proportio inaequalitatis est duarum quantitatum vel numerorum unius ad alterum certa habitudo ut proportio, quae est inter 2 et 4, pedale et bipedale. Item proportionum inaequalitatis quaedam est maioris inaequalitatis, quaedam vero minoris. Thomas 1509, S. 3.
Proportio maioris inaequalitatis est habitudo maioris quantitatis ad minorem ut habitudo, quae est inter quattuor et 2. Thomas 1509, S. 3.
Sed proportio minoris inaequalitatis est habitudo minoris quantitatis ad maiorem ut habitudo duorum ad 4. Thomas 1509, S. 3.
Ex quo sequitur, quod pro eisdem supponunt isti duo termini proportio maioris inaequalitatis et proportio minoris inaequalitatis. Connotat tamen iste terminus proportio maioris inaequalitatis, quod numerus maior excedat minorem. Iste vero terminus proportio minoris inaequalitatis connotat, quod numero minor sive quantitatis minor exceditur [...] a maiore. Quandoque tamen proportio maioris inaequalitatis non capitur pro aggregato ex numeris proportionem habentibus inaequalitatis, sed pro maiore numero, proportio vero minoris inaequalitatis pro minore. Et isto modo non sunt termini convertibiles. Nam isto modo capiendo, si 8 comparentur ad 4, 8 sunt proportio maioris inaequalitatis et 4 minoris inaequalitatis. Thomas 1509, S. 3.
Item proportio inaequalitatis est duplex, quia quaedem est rationalis, et quaedam irrationalis. Thomas 1509, S. 3.
Proportio rationalis est illa proportio, quae immediate denominatur ab aliquo certo numero vel numerorum fract[i]one ut dupla, sesquialtera et cetera. Alio modo proportio rationalis est duarum quantitatum sic se habentium, quod idem est pars aliquota utriusque, idem inquam ad bonum sensum. Thomas 1509, S. 3.
Ex quo sequitur, quod cuiuslibet numeri ad quemlibet alium numerum est proportio rationalis, quoniam cuiuslibet numeri unitas est pars aliquota. Unde pars aliquota est illa, quae aliquoties sumpta reddit suum totum adaequate, ut unitas est pars aliquota numeri quarternarii, quoniam unitas ter sumpta adaequate constituit ternarium, et quater sumpta quaternarium. Et dualitas est pars aliquota numeri octonarii, quoniam dualitas quater sumpta adaequate numerum octonarium constituit. Ex quo patet, quod dualitas non est pars aliquota numeri septenarii, quoniam non aliquoties sumpta reddit illud totum adaequate. Thomas 1509, S. 3f.
Proportio autem irrationalis est illa, quae non immediate ab aliquo numero denominatur. Alio modo proportio irrationalis est duarum quantitatum ita se habentium, quod nulla pars aliquota unius est pars aliquota alterius ut proportio, quae est inter diametrum et costam sui quadrati. Nam diameter excedit costam et non aliquoties nec per aliquam partem aliquotam vel per aliquas partes aliquotas, ut inferius probabitur in capitulo de proportione irrationali. Thomas 1509, S. 4.
Proportionum autem rationalium 5 sunt species, tres simplices et duae compositae. Simplices sunt istae: multiplex, superparticularis et suprapartiens. Compositae vero sunt multiplex, multiplex superparticularis, multiplex suprapartiens. Thomas 1509, S. 4.
Unde proportio multiplex est proportio, qua maius continet minus aliquoties ta[n]tum ut dupla, tripla. 4 enim continent 2 bis, et 6 continent 2 ter tantum. Et ideo inter illos numeros est proportio multiplex. Thomas 1509, S. 4.
Proportio vero superparticularis est proportio, qua maius continet minus semel tantum et aliquam partem eius aliquotam adaequate ut proportio sex ad 4. Nam 6 continet 4 semel tantum et medietatem, quae est pars aliquota ipsorum 4. Thomas 1509, S. 4.
Proportio autem suprapartiens est proportio, qua maius continet minus semel tantum et aliquot partes eius aliquotas, quae simul non faciunt aliquam eius partem aliquotam, ut proportio, quae est inter 7 et 5. Nam 7 continent 5 semel tantum et duas partes eius aliquotas, puta duas unitates. Thomas 1509, S. 4.
Sed proportio multiplex superparticularis est illa, qua maius continet minus aliquotiens et cum hoc aliquam eius partem aliquotam tantum ut proportio, quae est inter novem et 4. Nam 9 continent 4 bis et unam partem numeri quaternarii, puta unitatem. Thomas 1509, S. 4.
Proportio autem multiplex suprapartiens est illa, qua maius continent minus aliquotiens et aliquot partes eius aliquotas, quae non faciunt unam eius partem aliquotam ut proportio, quae est inter 11 et 4. Nam 11 continent 4 bis et tres partes aliquotas ipsorum 4, et illae non faciunt aliquam partem aliquotam ipsorum 4. Thomas 1509, S. 4.
Harum autem proportionum sive specierum proportionum sufficientia tali[] ratione haberi potest, ut adducit Albertus de Saxonia in suo tractatu de proportionibus post alios mathematicos. Quam omnis numerus sive quantitas ad aliam quantitatem habens rationalem proportio[n]em aut excedit eam aut exceditur ab illa. Si excedit eam, aut continet ipsam aliquoties aut semel tantum et aliquid ultra aut pluries et aliquid ultra. Si primum, tunc erit proportio multiplex. Si secundum, aut illud aliquid ultra est una pars eius aliquota adaequate, aut est plures partes aliquotae, quae non faciunt unam partem aliquotam. Si primum, sic est proportio superparticularis. Si secundum, est proportio superpartiens. Si vero maior quantitas continet minorem pluries et aliquid ultra, vel illud, quod ultra continet, est pars aliquota adaequate aut plures partes aliquotae, quae non faciunt unam. Si primum, sic est proportio multiplex superparticulares. Si secundum, sic est proportio multiplex suprapartiens. Et quia quantitas maior habens proportionem rationalem ad quantitatem minorem non potest pluribus modis ad illam referri sive comparari, quam his quinque modis. Consequens est, quod non possunt esse plures species proportionis rationalis his 5. Quandoquidem eodem modo venari potest minoris inaequalitatis proportionum sufficientia. Sola enim ratione proportio maioris inaequalitatis et minoris differunt). Thomas 1509, S. 4.
Omnis proportio sive omne genus proportionis infinitas habet species. Thomas 1509, S. 4.
Unde genus multiplicis habet infinitas species denominatas a naturali serie numerorum, puta duplam denominatam a binario, triplam a ternario, milleculpam a millenario, centuplam a centenario et sic in infinitum. Thomas 1509, S. 4.
Proportio enim dupla est illa, qua maius continet minus bis adaequate ut 4 cum 2, et tripla, qua maius continet minus ter adaequate, et quadrupla quater adaequate et sic in infinitum. Thomas 1509, S. 4.
Generantur autem omnes proportiones duplae, quae infinitae sunt, isto modo: disponatur primo series naturalis numerorum in una linea, et in alia linea inferiori disponantur omnes numeri excedentes se binario incipiendo a binario in infinitum, et isto modo comparando primum superioris lineae primo inferioris et secundum secundo et tertium tertio et sic in infinitum invenientur infinitae proportionis duplae. In praesenti figura clare hoc poteris conspicere. Per naturalem seriem numerorum intelligas ordine numerorum incipiendo ab unitate nullum numerum omittendo ut 1, 2, 3, 4 et cetera. Thomas 1509, S. 4.
Sed infinitae proportiones triplae isto modo generantur: disponantur omnes numeri secundum seriem naturalem numerorum incipiendo ab unitate in una linea, et in linea inferiori disponantur omnes numeri excedentes se ternario. Et tunc comparando primum inferioris ordinis primo superioris et secundum secundo et tertium tertio habebuntur infinitae proportiones triplae. Thomas 1509, S. 4.
Si vero velis generare omnes proportiones quadruplas, capias numeros excedentes se quaternario incipiendo a numero quaternario cum serie naturali numerorum. Si autem quintuplam, capias omnes excedentes se quinario. Si sextuplam senario et sic in infinitum, ut facile est videre in figuris sequentibus. Thomas 1509, S. 4.
Superparticularis autem proportio etiam infinitas habet species denominatas a partibus aliquotis et unitate, puta a medietate, a tertia, quarta, quinta et sic in infinitum. Et ideo prima species eius et maxima dicitur sesquialtera, secunda vero sesquitertia, sesquiquarta, sesquiquinta et sic in infinitum. Unde „sesqui“ idem est quod totum, et „altera“ idem est quod medietas, et sic p[ro]portio sesquialtera est, qua maius continet minus semel tantum et medietatem eius. „Sexquitertia“ vero est, qua maius continet minus semel tantum et unam tertiam eius. Et „sesquiquarta“, qua maius continet minus semel tantum et unam quartam eius et sic in infinitum. Thomas 1509, S. 4f.
Generantur autem species huius proportionis isto modo: capiatur ordo naturalis numerorum incipiendo a binario, et comparetur secundus primo, et tertius secundo, et quartus tertio et sic in infinitum, et habebuntur omnes species huius proportionis sereatim. Si autem libet infinitas sesquialteras procreare, capientur in una linea omnes numeri excedentes se binario, et in alia omnes numeri excedentes se ternario, et comparetur primus inferioris primo superioris, et secundus secundo et sic in infinitum. Si vero in uno ordine ponantur omnes numeri excedentes se ternario, et in alio excedentes se quaternario, secunda species producetur, puta sesquitertia. Si autem in uno ponantur omnes excedentes se quaternario, et in alio quinario, producetur tertia species, puta sesquiquarta, et sic in infinitum in aliis speciebus, ut patet in figuris sequentibus. Thomas 1509, S. 5.
Proportio suprapartiens infinitas habet species, videlicet superbipartiens tertias, superbipartiens quintas, supertripartiens quartas et sic in infinitum. Unde proportio superbipartiens tertias est, qua maius continet minus semel tantum et duas tertias minoris. Unde in quolibet nomine huius speciei ponuntur duo numeri. Primus numerus denotat numerum partium aliquotarum. Et secundus denotat denominationes illarum, ut cum dicimus superbipartiens tertias. ly „bi“ dicit numerum partium aliquotarum, quas dicit esse duas, et ly „tertias“ dicit illas esse tertias partes numeri minoris et sic exemplifica in aliis. Thomas 1509, S. 5.
Generantur autem infinitae species huius proportionis isto modo: capiatur in una serie naturalis ordo numerorum incipiendo a ternario, et in alia omnes impares incipiendo a quinario, et comparetur primus unius ordinis primo alterius, et secundus secundo et sic in infinitum, et habebuntur infinitae species huius proportionis, ut patet in figura. Thomas 1509, S. 5.
Proportio autem multiplex superparticularis multas habet species, puta duplam sesquialteram, duplam sesquitertiam, triplam sesquialteram, triplam sesquitertiam et sic in infinitum, quarum specierum definitiones patent ex dictis. Generantur autem infinitae species eius hoc modo: capiatur in uno ordine naturalis series numerorum incipiendo a binario, et in alio ordine capiantur omnes numeri excedentes se quinario a quinario exordiendo, et comparando primum unius ordinis primo alterius constabitur prima species, et referendo secundum secundo educetur secunda et sic in infinitum, ut patet in figura. Thomas 1509, S. 5.
Hier wird deutlich, dass die Eins nur bedingt als Zahl aufgefasst wird. Mit der ersten Zahl ist die Zwei gemeint, wie in der anschließenden Darstellung deutlich wird.
Proportio vero multiplex superparticularis infinitas habet species, quarum quaelibet in infinitas etiam pa[r]titur species, puta duplam superparticularem, triplam superparticularem, quadruplam superparticularem et sic in infinitum. Unde ad procreandas infinitas duplas superparticulares capiantur duae series numerorum, et in prima ponatur naturalis series numerorum incipiendo a binario, in alia vero ponantur omnes numeri impares a quinario inchoando, et tunc referendo primum inferioris primo superioris, et secundum inferioris secundo superioris et sic consequenter habebuntur infinitae species huius duplae superparticularis. Sed ad producendas infinitas triplas superparticulares constituatur in prima serie naturalis ordo numerorum se mota unitate, et in secunda capiantur omnes numeri excedentes se ternario incipiendo a septenario, tunc modo iam saepius dicto referendo numeros infinitas triplas superparticulares educes. Ad generandas vero infinitas quadruplas superparticulares constituatur naturalis series numerorum a primo numero inchoando in linea superiori, in inferiori vero ordinetur quaedam series numerorum continu[o] excedentium se quaternario inchoando a novenario. Ad generandam autem sequentem speciem, puta quintuplam superparticularem, capias pro primo ordine naturale[m] seriem numerorum, quam pro qualibet specie debes capere, et pro secundo omnes numeros excedentes se quinario incipiendo ab undenario, et pro sequenti specie, puta sextupla superparticulari, capiantur omnes numeri excedentes se senario incipiendo a tridenario numero, pro alia excedentes se septenario inchoando a quindenario et sic in infinitum, ut patet in figuris sequentibus. Thomas 1509, S. 5.
Proportio vero multiplex suprapartiens infinitas habet species, ut dupla suprabipartiens tertias, tripla suprabipartiens tertias et sic in infinitum coadunando omnes species proportionis multiplicis cum qualibet suprapartiente et econverso. Et infinitas similiter habet species, quarum quaelibet in infinitas etiam partitur species, ut puta dupla suprapartiens in duplam suprabipartientem tertias, in duplam suprabipartientem quintas, in duplam suprabipartientem quartas et sic in infinitum. Genera[]tur autem dupla superpartiens isto modo: constituatur naturalis series numerorum incipiendo a ternario, quae semper debet esse prima in qualibet specie tali, et in linea inferiori ponantur omnes numeri excedentes se ternario inchoando ab octonario. Pro generatione vero triplae suprapartientis in secunda serie ponantur omnes numeri excedentes se quaternario incipiendo ab undenario. Pro generatione autem quadruplae suprapar[t]ientis ponantur in secunda serie omnes numeri excedentes se quinario incipiendo a quatuordecim. Et pro sequenti specie capiantur omnes excedentes se senario, et pro alia septenario et sic in infinitum, ut patet in figuris sequentibus. Thomas 1509, S. 5.
[...] proportio quadratorum superficialium est proportio costarum dublicata. Hoc est, si inter costas duorum quadratorum superficialium sit aliqua proportio maioris inaequalitatis, inter quadrata erit proportio dupla ad illam, quae est inter costas signatorum quadratorum, ut si inter costas duorum quadratorum inaequalium superficialium fuerit proportio dupla, inter quadrata erit proportio quadrupla. Thomas 1509, S. 6.
Vgl. Thomas 1509, S. 6.
[...] quadratum diametri se habet ad quadratum costae in proportione dupla. Hoc est, quadratum, cuius qua[e]libet costa est aequalis diametro alicuius quadrati, se habet in proportione dupla ad illud quadratum. Thomas 1509, S. 6.
Probatur haec suppositio, et sit unum quadratum magnum, cuius latus sit DC et diameter sit AC, sitque aliud parvum cum isto communicans, cuius costa sit CF, et diameter sit DC, et dividatur quadratum maius per duos diametros in quatuor triangulos aequales, ut patet in hac figura. Quo posito arguitur sic: magnum quadratum est duplum ad parvum quadratum, et ipsum magnum quadratum est quadratum diametri ipsius parvi quadrati, ut patet manifeste, igitur quadratum diamet[r]i se habet ad quadratum costae in proportione dupla. Consequentia patet cum minore, et arguitur maior, quia quadratum magnum continet quater medietatem parvi quadrati adaequate, igitur ipsum magnum quadratum continet bis adaequate parvum quadratum. Consequentia patet ex se, et probatur antecedens, quia quadratum magnum quater continet tantum, sicut est triangulus DEC, ut patet, et ille triangulus est medietas parvi quadrati, ut manifeste patet in figura. Igitur magnum quadratum quater continet adaequate mediante parvi. Quod fuit probandum. Thomas 1509, S. 6.
[...] diametri ad costam est proportio, quae est medietas duplae. Probatur, quia quadrati diametri ad quadratum costae est proportio dupla, ut patet ex secunda suppositione. Ergo diametri ad costam est proportio subdupla ad duplam, et per consequens medietas duplae. Thomas 1509, S. 6.
[...] cui[u]slibet proportionis suprapartientis alter primorum numerorum est impar. Sunt autem primi numeri alicuius proportionis, qui in ea proportione sunt numeri, ut tria et 2 sunt primi numeri proportionis sesquialterae, quia in naturali serie numerorum inter nullos minores proportio sesquialtera invenitur. Thomas 1509, S. 6.
Vgl. Thomas 1509, S. 6.
[...] omne quadratum numeri imparis est impar. Thomas 1509, S. 6.
Vgl. Thomas 1509, S. 6.
[...] nullus numerus impar est duplas ad aliquem numerum. Thomas 1509, S. 6. Hier wird offensichtlich, dass es sich um den Bereich der natürlichen Zahlen handelt.
[...] nulla proportio diametri ad costam est multiplex aut multiplex superparticularis aut multiplex suprapartiens. Thomas 1509, S. 6.
[...] nulla proportio diametri ad costam est aliqua proportio superparticularis. Thomas 1509, S. 6.
[...] nulla proportio diametri ad costam est aliqua proportio suprapartiens. Thomas 1509, S. 7.
Aliquam autem quantitatem se habere ut numerus impar respectu alterius est ipsam dividi saltem ad imaginationem in partes aequales denominatas a numero impari ut in tres tertias, in quinque quintas, in septem septimas et sic consequenter et hoc respectu alterius quantitatis divisae in partes illis aequales, ut si pedale dividatur in tres tertias, et bipedale in sex sex[t]as, quarum sextarum quaelibet est aequalis uni tertiae pedalis, tunc dico, quod pedale se habet ut numerus impar respectu bipedalis. Tu tamen adverte, quod etiam potest se habere ut numerus par respectu bipedalis, tamen semper inter pedale et bipedale erit proportio dupla. Diameter autem et costa numquam sic se possunt habere, quod diameter se habeat ut numerus impar respectu costae vel econtra, ut probatum est. Thomas 1509, S. 7.
[...] omnis proportio diametri ad costam est irrationalis. Thomas 1509, S. 7.
Proportio irrationalis perinde atque rationalis in infinitas distribuitur species. Thomas 1509, S. 7.
[...] si duae quantitates se habent ut duo numeri, aggregatum ex eis se habebit ut unus numerus. Probatur, quia semper ex additione numeri ad numerum resultat numerus maior. Thomas 1509, S. 7.
[...] si aliquae quantitates se habeant in proportione rationali, illae se habebunt ut duo numeri et econtra. Thomas 1509, S. 7.
[...] si duae quantitates se habeant in proportione rationali, aggregatum ex eis se habet in proportione rationali ad quamlibet illarum quantitatum. Thomas 1509, S. 7.
[...] costae ad excessum, quo diameter excedit costam, [est] proportio irrationalis. Thomas 1509, S. 7.
[...] si quantitatis maioris ad aliquam partem aliquota[m] quantitatis minoris sit proportio rationalis, eiusdem quantitatis maioris ad totam quantitatem minorem erit proportio rationalis. Thomas 1509, S. 8. Der pars aliquota wird im Kapitel 1.1 definiert.
[...] si duae quantitates inaequales se habeant in proportione rationali, utraque illarum se habet ad excessum, quo maior excedit minorem, in proportione rationali vel aequalitatis. Thomas 1509, S. 8.
[...] infinitae sunt species proportionis irrationalis minores dupla, et illarum in infinitum parva est aliqua. Thomas 1509, S. 8.
Vgl. Thomas 1509, S. 8.
[...] infinitis modis possunt generari infinitae species minores dupla irrationalis proportionis, utpote si excessus diametri diminuatur per partes proportionales proportione dupla. Alio modo proportione tripla, alio quadrupla, alio sesquialtera et sic in infinitum. Thomas 1509, S. 8.
[...] infinitae sunt species proportionis irrationalis maioris dupla, et illarum infinite magna est aliqua. Thomas 1509, S. 8.
Vgl. Thomas 1509, S. 8f.
[...] non omnes partes alicuius corporis, in quas idem corpus dividitur, continuo se habentes in eadem proportione, gratia exempli [...] sunt omnes partes proportionales eiusdem corporis eadem proportione A. Probatur, quia possibile est, quod una medietas alicuius corporis dividatur in omnes partes suas proportione tripla, et omnes illae partes sunt partes illius corporis totalis, in quas idem corpus dividitur, habentes se continuo in proportione tripla, et tamen non sunt omnes partes proportionales illius corporis proportione tripla. Thomas 1509, S. 9.
[...] omnes partes alicuius corporis innuitae continu[o] se habentes aliqua proportione, puta A, et absolventes totum corpus sunt omnes partes proportionales eiusdem corporis proportione A. Et volo dicere, quod si aliquod corpus dividatur in infinitas partes continuo se habentes in proportione A et absolventes totum corpus, illae simul sunt omnes partes proportionales proportione A. Thomas 1509, S. 9.
[...] quandocumque aliqua continuo proportionantur aliqua proportione geometrica, qualis est proportio inter proportionata, talis est inter suas differentias sive excesseus, quod idem est, ut quia [8] ad 4 se habet in proportione dupla, et similiter 4 ad 2, et continuo proportionantur eadem proportione, ideo differentia sive excessus inter 8 et 4 se habet ad differ[en]tiam sive excessum inter 4 et 2 in proportione dupla. Thomas 1509, S. 9.
[...] si aliquod corpus dividatur in infinitas partes, et deperdendo primam illarum perdit aliquam proportionem, puta A, hoc est, efficitur in A proportione minus, et perdendo secundam post primam iterum efficitur in A minus, et perdendo tertiam post secundam iterum efficitur in A minus, et sic consequenter illae partes sunt omnes partes proportionales illius corporis proportione A, si vero perdendo primam illarum non perdit unam proportionem A, et perdendo secundam post primam unam alteram, perdendo tertiam post secundam unam alteram proportionem A et sic consequenter, tales partes non sunt omnes partes proportionales talis corporis proportione A. Thomas 1509, S. 9.
[...] quandocumque aliquod corpus dividitur quovis genere proportionis, totum corpus se debet habere ad aggregatum ex omnibus partibus proportionalibus sequentibus primam in ea proportione, qua corpus dividitur. Thomas 1509, S. 10.
[...] ad inveniendum residuum a prima parte proportionali quavis proportione rationali corpus dividatur, capiantur primi numeri talis proportionis, et dividatur corpus in tot unitates, quotus est numerus maior illius proportionis, et ex illis partibus pro residuo a prima parte capiantur tot, quotus est numerus minor talis proportionis. Thomas 1509, S. 10.
[...] ad dividendum corpus per partes proportionales quavis proportione multiplici capienda est pro residuo a prima parte proportionali una pars aliquota denominata a numero talem proportionem multiplicem denominante, ut in divisione dupla proportione capienda est una medietas pro residuo a prima parte proportionali, et proportione tripla una tertia, et quadrupla una quarta, quintupla vero una quinta et sic in infinitum. Thomas 1509, S. 10.
[...] dividendo corpus proportione dupla prima pars erit medietas, et secunda medietas residui, et tertia medietas residui et sic consequenter, proportione tripla prima pars est duae tertiae totius, et secunda duae tertiae residui, et tertia duae tertiae residui a prima et secunda et sic sine termino, proportione vero quadrupla prima pars est tres quartae, et secunda tres quartae residui, proportione vero quintupla prima pars est quatuor quintae et sextupla quinque sextae, et septupla sex septimae et sic sine termino. Thomas 1509, S. 10.
[...] dividendo corpus per partes proportionales proportione dupla residuum a prima est aequale primae parti, et proportione tripla est subduplum ad primam, et quadrupla subtriplum, et quintupla subquadruplum, et sextupla subquintuplum et sic sine termino. Thomas 1509, S. 10.
Si enim dividendo proportione tripla prima pars est duae tertiae, et residuum una tertia, cum una tertia sit subduplum ad duas tertias, residuum a prima dividendo proportione tripla erit subduplum ad primam. Item cum dividendo corpus proportione quadrupla prima pars sit tres quartae, et residuum a prima una quarta, una autem quarta est subtripla ad tres quartas, igitur residuum a prima parte dividendo proportione quadrupla est subtriplum ad primam partem. Et hoc modo de aliis probabis. Thomas 1509, S. 10.
[...] ad dividendum corpus quavis proportione superparticulari capienda est pro prima parte proportionali una pars aliquota denominata a maiori numero primorum numerorum talis proportionis. Thomas 1509, S. 10.
[...] diviso corpore per partes proportionales proportione sesquialtera residuum a prima parte est duplum ad primum, et sesquitertia triplum, et sesquiquarta quadruplum, et sesquiquinta quintuplum et sic in infinitum, opposito modo ad species proportionis multiplicis incipiendo a tripla. Thomas 1509, S. 11.
[...] ad dividendum corpus, qua placuerit, proportione suprapartienti generentur species huius proportionis sereatim modo posito in secundo capite huius partis, et dividatur corpus in tot partes, quotus est numerus inferioris ordinis, et ex illis partibus capiantur tot pro residuo a prima parte proportionali, quotus est numerus superior, et residuum erit prima pars proportionalis. Thomas 1509, S. 11.
Exemplum, ut constituatur naturalis series numerorum incipiendo a ternario, et constituatur inferus series omnium numerorum imparium incipiendo a quinario, ut patet in figura. Thomas 1509, S. 11.
Tunc si vis dividere aliquod corpus in proportione suprabipartiente tertias, quia numerus inferior in illa specie est quinarius dividas totum corpus in quinque quintas, et quia numerus superior est ternarius, capias pro residuo a prima parte proportionali tres quintas, et manebunt duae quintae, et illae duae quintae sunt prima pars proportionalis proportione suprabipartiente tertias. Et isto modo in omnibus aliis speciebus operaberis. Et quam in capite secundo, ubi generantur species huius proportionis, non omnes generantur, quamvis generentur infinitae. Ideo ad dividendum corpus, qua volueris, proportione suprapartiente utaris doctrina secundae conclusionis. Thomas 1509, S. 11.
[...] in divisione corporis prima specie proportionis suprapartientis signatae inferius residuum a prima parte proportionali est sesquialterum ad primam, et in secunda specie residuum a prima est sesquitertium ad primam, et in tertia specie est sesquiquartum ad primam, et in quarta residuum a prima erit sesquiquintum ad primam et sic in infinitum procedendo per species proportionis superparticularis. Thomas 1509, S. 11.
[...] ad dividendum corpus, qua volueris, proportione multiplici superparticulari generentur in numeris species huius proportionis modo posito in secundo capite huius partis, et dividatur corpus in tot partes, quotus est numerus inferioris ordinis, et ex illis partibus capiantur tot pro residuo a prima parte proportionali, quotus est numerus superior, et residuum erit prima pars proportionalis. Et eodem modo fiat dividendo proportione multiplici suprapartiente ut ad dividendum corpus proportione dupla sesquialtera, quia numerus maior in illa specie est quinarius, dividatur corpus in quinque quintas, et quia numerus minor est binarius capiantur duae quintae pro residuo a prima parte proportionali, et tres quintae erunt prima pars proportionalis, et tres quintae residui secunda, et iterum tres quintae residui a prima et secunda, tertia et sic sine termino. Item si vis dividere corpus proportione dupla suprabipartiente tertias dividas corpus in octo octavas, quia numerus octonarius est numerus maior illius proportionis, et capias pro residuo a prima parte proportionali tres octavas, et residuae quinque octavae erunt prima pars proportionalis, et quinque octavae residui erunt secunda pars proportionalis et sic consequenter. Thomas 1509, S. 11.
Ex quo sequitur, quod in omnibus speciebus proportionis multiplicis superparticularis aut multiplicis suprapartientis et etiam in omnibus aliis residuum a prima parte proportionali habet se ad primam partem proportionalem in ea proportione, qua se habent numeri superiores in figuris suarum generationum ad numeros, per quos inferiores excedunt superiores, ut in proportione dupla sesquialtera, quia numerus superior est binarius, et numerus inferior quinarius, et quinarius excedit binarium per ternarium, residuum a prima parte proportionali in tali proportione se habet ad primam partem proportionalem sicut duo ad tria, et quia in proportione dupla suprabipartiente tertias numerus superior est ternarius, et inferior octonarius, et octonarius excedit ternarium per quinarium, ideo in talis proportionis divisione residuum a prima parte proportionali se habet ad primam sicut quinarius ad ternarium. Thomas 1509, S. 11.
Ad habendam autem praxim huius correlarii in compositis proportionibus constituentur aliquae figurae, quibus facile iudicabitur, in qua proportione se habet residuum a prima parte proportionali ad primam partem proportionalem. Thomas 1509, S. 12.
Ad quod facile inspiciendum in proportionibus duplis superparticularibus constituatur naturalis series numerorum incipiendo a binario in inferiori linea, et in superiori linea constituatur naturalis ordo numerorum incipiendo a ternario, tunc referendo primum inferioris ordinis primo superioris habebis, in qua proportione se habet residuum a prima parte proportionali ad primam dividendo corpus prima specie proportionis duplae superparticularis, et referendo secundum inferioris ordinis secundo superioris habebis illud idem in secunda specie proportionis duplae superparticularis et sic consequenter, ut patet in figura. Thomas 1509, S. 12.
Sed ad praxim huius negotii in speciebus proportionis triplae superparticularis constituatur in inferiori serie naturalis ordo numerorum incipiendo a binario, et in superiori constituantur omnes numeri impares incipiendo a quinario, et tunc referendo primum inferioris ordinis primo superioris et secundum inferioris secundo superioris et tertium inferioris tertio superioris et sic consequenter conspicies, in qua proportione se habet residuum a prima parte proportionali ad primam divisione corporis facto proportione tripla superparticulari, ut patet in figura. Thomas 1509, S. 12.
Ad praticandum autem ita in speciebus quadruplae superparticularis, quintuplae superparticularis et cetera constituatur naturalis series numerorum incipiendo a binario in linea inferiori, et in superiori omnes numeros excedentes se continuo ternario incipiendo a septenario, et sic habebis, quod quaeris in speciebus proportionis quadruplae superparticularis. Ad quod inveniendum in speciebus proportionis quintuplae superparticularis constituas in superiori ordine omnes numeros excedentes se quaternario incipiendo a numero novenario, et in specie seque[n]ti costituas in superiori ordine omnes numeros excedentes se quinario incipiendo a numero undenario, et sic consequenter in aliis speciebus operaberis. Patet hoc in figuris sequentibus. Thomas 1509, S. 12.
Sed ad exercitium huius ultimi correlarii in speciebus multiplicium suprapartientium quaedam etiam constituentur figuere. Unde ac facile inveniendam proportionem residui a prima parte proportionali ad ipsam primam in speciebus proportionis duplae suprapartientis constituatur naturalis series incipiendo a ternario inferiori linea, in superiori vero constituantur omnes numeri impares incipiendo a quinario, et tunc referendo primum inferioris ordinis primo superioris, et secundum secundo, et tertium tertio id, quod quaeris, facile reperies, ut patet in figura sequenti. Thomas 1509, S. 12.
Ad inveniendam autem proportionem residui a prima parte proportionali ad ipsam primam divisione corporis facta proportione tripla suprapartiente constituatur supra naturalem seriem numerorum incipiendo a ternario una series omnium numerorum continuo excedentium se ternario incipiendo ab octonario numero, ut patet in figura. Thomas 1509, S. 12.
Ad inveniendum autem propositum in speciebus proportionis quadruplae suprapartientis supra naturalem seriem numerorum incipiendo a ternario constituatur series numerorum continuo excedentium se quaternario incipiendo ab unde[n]ario, et sic consequenter [in speciebus proportionis quadruplae suprapartientis] supra eandem naturalem seriem numerorum incipiendo a ternario constituatur series numerorum continuo exedentium se numero quinario incipiendo a numero quarto decimo, et sic consequenter operaberis in aliis. Et haec de divisione corporum proportione rationali. Thomas 1509, S. 12.
Quemadmodum quodlibet corpus dividi potest proportione rationali infinitisque speciebus eius, ut caput praecedens ostendit, ita etiam proportione irrationali infinitisque speciebus eius quodlibet corpus dividi potest. Thomas 1509, S. 12.
[...] quodlibet corpus divisum aliqua proportione irrationali se debet habere ad aggregatum ex omnibus partibus proportionabilibus tali proportione sequentibus primam in ea proportione, qua totum dividatur. Thomas 1509, S. 12.
[...] ad dividendum corpus infinitis proportionibus irrationabilibus minoribus dupla, ut puta proportione diametri ad costam, aggregati ex medietate excessus, quo diameter excedit costam, et ipsa costa [ad] ipsammet costam et sic consequenter, ut capite quarto ostensum est, debet pro prima parte capi excessus, quo maior quantitas excedit minorem, ita quod residuum a prima sit minor quantitas, et totum corpus sit maior quantitas talis proportionis. Thomas 1509, S. 12f.
[...] ad dividendum corpus proportione irrationali diametri ad costam oportet pro prima parte proportionali capere excessum, quo diameter excedit costam, et pro secunda capere etiam excessum, quo illa costa, cum est diameter quadrati, excedit costam illius quadrati, et sic consequenter. Et ad dandam primam partem proportionale proportionis irrationalis, quae est aggregati ex costa et medietate excessus diametri ad ipsam costam, capiatur pro prima parte proportionali illa medietas excessus, et pro secunda parte proportionali capiatur tanta pars residui, ad quam prima habeat illam proportionem, quae est totius corporis ad aggregatum ex omnibus sequentibus primam, et iterum in residuo a prima parte et secunda pro tertia parte capiatur tanta pars, ad quam secunda habeat illam proportionem, quam prima habet ad ipsam, et sic consequenter. Et simili modo operandum esset, si divideretur corpus proportione irrationali, quae est aggregati ex costa et quarta parte vel octava vel decimasexta excessus, qu[o] diameter excedit costam, ad ipsam costam. Thomas 1509, S. 13.
[...] diviso corpore per partes proportionales proportione irrationali, quae est diametri ad costam, omnes partes impares continuo se habent in proportione dupla, et omnes pares similiter, et omnes duae, inter quas mediant duae, se habent continuo in proportione sesquialtera ad duplam, et omnes, inter quas mediant tres, se habent in proportione quadrupla et sic consequenter. Thomas 1509, S. 13.
Patet hoc correlarium sensui in figura sequenti, in qua prima pars est diameter quadrati maioris ibidem positi, et secunda est costa eiusdem quadrati, et tertia est costa quadrati sequentis, et tertia est costa tertii quadrati, et diameter quarti, et quarta est costa quarti quadrati, et diametri quinti, et quinta est costa ipsius quinti quadrati, et sic in infinitum poteris procedere, ibi enim conspicies, quod primae ad tertiam est proportio dupla et secundae ad quartam etiam dupla, et primae ad quintam est quadrupla. Thomas 1509, S. 13.
Ex quo sequitur tertio, quod in tali divisione aggregatum ex omnibus imparibus a prima impari est aequale primae, et aggregatum ex omnibus paribus a secunda, quae est prima par, est aequale secundae, et aggregatum ex omnibus imparibus se habet ad aggregatum ex omnibus paribus in proportione, quae est medietas duplae. Thomas 1509, S. 13.
[...] diviso corpore per partes proportionales proportione irrationali, quae est medietas triplae, omnes partes impares talis divisionis se habent in proportione tripla, et etiam omnes pares, et omnes, inter quas mediant tres, in proportione novocupla, et aggregatum ex omnibus imparibus se habet ad aggregatum ex omnibus paribus in proportione, quae est medietas triplae. Thomas 1509, S. 14.
[...] ad dividendum corpus in partes proportionales infinitis speciebus proportionis irrationalis maioris dupla, ut puta proportione, quae est totius diametri ad excessum, quo ipsa diameter excedit costam, et totius diametri cum medietate excessus, quo excedit costam, vel ad quarta[m] [...] vel ad quintam vel ad sextam, ut superius dictum est, pro prima parte proportionali capiendus est excessus, quo quantitas maior excedit minorem in tali proportione, et quantitas minor [capienda est] pro residuo, ut si velis partiri corpus in partes proportionales proportione, quae est totius diametri ad excessum, quo diameter excedit costam, capienda est costa quadrati, cuius illud corpus dividendum est, diameter pro prima parte proportionali, et sic pro residuis maneat excessus, qu[i] est quantitas minor talis proportionis, et pro secunda capienda est costa quadrati, cuius totum aggregatum ex omnibus sequentibus primam est diameter, et ad dandam tertiam capiatur costa quadrati, cuius est diameter aggregatum ex omnibus sequentibus primam et secundam. Et ad dividendum aliquod corpus proportione, quae est totius diametri ad medietatem excessus, quo excedit costam, pro prima parte proportionali capiendus est excessus, quo maior quantitas excedit minorem tali proportione. Constituendum enim est totum corpus, diameter alicuius quadrati, et tunc pro prima parte proportionali capienda est tanta pars illius corporis, quod pro omnibus sequentibus non maneat nisi medietas excessus, quo tale corpus existens diameter excedit costam eiusdem quadrati, et addandam secundam partem proportionalem constituatur totum, quod sequitur primam diameter alicuius quadrati, et pro secunda parte capiatur tantum, quod pro sequentibus non maneat nisi medietas excessus, quo talis diameter excedit suam costam, et sic consequenter. Thomas 1509, S. 14.
Vgl. Thomas 1509, S. 14.
Vgl. Thomas 1509, S. 14.
[...] diviso corpore per partes proportionales quavis proportione et captis certis ordinibus partium proportionalium interscalariter se habentium totumque corpus absolventibus tunc illi ordines se habent continuo in proportione divisionis, ut si corpus dividatur proportione dupla, et capiantur omnes partes, inter quas mediant duae, pro primo ordine, puta prima, quarta, septima, decima, tridecima et cetera, et deinde pro secundo ordine secunda, quinta, octava, undecima, decima quarta et sic consequenter, et demum pro tertio ordine capiantur tertia, sexta, nona, duodecima, quindecima et sic deinceps. Dico, quod primus ordo se habet ad secundum in proportione dupla, et etiam secundus ad tertium in proportione dupla. Thomas 1509, S. 14.
[...] qua[n]documque aliqua dividuntur aequali proportione, in quacumque proportione se habent primae partes proportionales, in eadem proportione se habent, et ipsa tota, quoniam sunt partes aliquotae eiusdem denominationis. Modo in quacumque proportione se habent partes aliquote eiusdem denominationis, in eadem se habent, et ipsa tota, quorum sunt partes aliquotae, ut postea demonstrabitur. Igitur. Thomas 1509, S. 14.
[...] ad sciendum, quota pars vel quotae partes aliquotae est quilibet illorum ordinum, videndum est, quot sint ordines, et tunc constituantur in numeris tot proportiones divisionis, quot sunt illi ordinis dempta una, et coadunentur omnes termini illarum proportionum, et dividatur totum in tot partes aliquotas, quotus est numerus resultans, et dentur primo ordini tot ex illis partib[u]s, q[u]otus est maximus numerus in illis proportionibus, et secundo ordini tot, quotus est secundus numerus, et sic consequenter. Et sic videbis, quot partes aliquotas et cuius denominationis continet primus ordo et secundus et tertius et sic consequenter. Thomas 1509, S. 14.
[...] alicuius continui partes aliquota[e] proportionem aliquam rationalem acquirente proportionem acquisitam toti invenire ut divisio corpore in quinque partes aliquotas, putas in 5 quintas, una illarum quintarum acquirente proportionem duplam, invenire, quantam proportionem totum illud corpus proportionem acquirat. In illo enim casu illud corpus proportionem sesquiquintam acquirit, cum acquirat supra se unam quintam, hoc est tantum, quanta est una eius quinta[e]. Thomas 1509, S. 15.
Si autem acquirit rationalem, non multiplicem, manifestum est, quod illa denominatur ab aliqua parte aliquota vel ab aliquibus partibus aliquotis adaequate vel inadaequate (non est modo cura), sicut dupla sesquitertia denominatur a numero binario cum tertia, et suprabipartiens tertias ab unitate cum duabus tertiis. Thomas 1509, S. 15.
Si autem una illarum septimarum acquirat duplam sesquitertiam, dividas quamlibet septimam etiam in tertias, et multiplica septem per tria, et reperies, ut dictum est viginti unum, et quia una septima acquisivit tantum, quanta ipsa est, puta unam septimam totius cum una tertia illius septimae, dividas etiam illam septimam acquisitam in tres partes, et illae tres partes erunt tres vicesime primae totius, ut constat, et totum acquisivit illas tres et cum hoc unam. Thomas 1509, S. 15.
Et isto modo in omni alia specie proportionis operaberis. Et ex hoc poteris invenire proportionem, quam acquirit totum duabus partibus eius aliquotis inaequalibus sive duabus non facientibus unam sive pluribus acquirentibus aequalem proportionem vel etiam inaequalem. Et consimiliter cognosces, quam proportionem deperdit totum aliqua parte eius vel aliquibus partibus aliquotis aliquam vel aliquas proporti[o]nes deperdente vel deperdentibus. Thomas 1509, S. 15.
Vgl. Thomas 1509, S. 15.
Suppono primo, quod duplex est numerus, ut ad propositum sufficit, quidam est compositus ex unitatibus divisibilibus, [...] cuius quaelibet unitas est res divisibilis ut numerus trium pedalium, quattuor qualitatum et cetera, alius vero numerus est compositus ex unitatibus indivisibilibus ut numerus 5 punctorum, 5 intelligentiarum et 10 animarum rationalium. Thomas 1509, S. 15f.
[...] non omnis numerus habet subduplum, nec omnis habet subtriplum et sic consequenter. Probatur, quoniam aliquis numerus, puta rerum indivisibilium, cuiusmodi est: numerus ternarius angelorum non potest dividi in duo aequalia, igitur non habet subduplum, nec in quatuor partes aequales, et sic non habet subquadruplum, et sic probatur de aliis, igitur suppositio vera. Thomas 1509, S. 16.
[...] omnis numerus rerum divisibilium habet subduplum, subtriplum, et universaliter omnem proportionem minoris inaequalitatis et etiam maioris aut[em] habere potest. Probatio huius suppositionis, quia talis numerus potest dividi in duo aequalia, cum sit numerus rerum divisibilium, et in tria aequalia et in 4 et in 5 et sic in infinitum. Quare dabitur quilibet numerus habens proportionem minoris inaequalitatis ad ipsum et etiam maioris. Nam ad sui medietatem habebit proportionem duplam, ad tertiam triplam, ad duas tertias sesquialteram et sic in infinitum. Thomas 1509, S. 16.
[...] ad dividendum numerum aliquem per alterum sive maiorem, sive minorem, sive aequalem, sive oporteat uti fractione, sive non [fractione] dividenda est quaelibet unitas numeri dividendi in tot partes aliquotas, quotus est numerus, per quem fit divisio, et dandae sunt tot partes illarum cuilibet unitati numeri, per quem fit divisio, quotus est numerus dividendus, et sic quaelibet unitas habebit aequaliter. Thomas 1509, S. 16.
[...] ad dividendum numerum se habentem, in qua volueris, proportione minoris inaequalitatis [ad eum,] ad quemcumque numerum volueris, capias in numeris duos numeros se habentes in tali proportione, et dividas numerum respectu, cuius quaeris numerum se habentem in proportione minoris inaequalitatis in tot partes aequales, quotus est numerus maior talis proportionis, et ex his capias tot illarum partium, quotus est numerus minor dictae proportionis. Thomas 1509, S. 16.
[...] ad inveniendum numerum se habentem in proportione maioris inaequalitatis [ad eum], ad quem volueris, numerum, et in quacumque libuerit proportione, capias in numeris duos numeros se habentes in tali proportione, et dividas numerum respectu, cuius quaeris numerum se habentem in illa proportione maioris inaequalitatis in tot partes aequales, quotus est numerus minor talis proportionis, et tunc illi numero minori sic divis[]o addas tot aequales partes partibus divisionis, quot sunt, per quas numerus maior talis proportionis excedit minorem. Et tunc numerus resultans ex n[u]mero minori et illa additione est numerus se habens ad numerum sic divisum in pr[o]portione data maioris inaequalitatis. Thomas 1509, S. 16.
